October 19, 2019 12:00

안녕하세요. rdd6584로 활동하고 있는 권일우입니다.

이 글에서는 요즘 유행하는 segment tree beats(이하 세그비츠)에 대해서 소개하겠습니다. 이를 위해서는, segment tree with lazy propagation에 대한 지식이 선행되어야 하지만 여기서는 소개하지 않겠습니다.

Segment Tree Beats

segment tree beats의 beats는 일본 애니메이션 “angel beats”에서 따온 것으로 특별한 의미를 가지고 있지 않습니다. 그러면 세그비츠가 뭘까요? 세그비츠는 lazy propagation의 활용형으로 중단조건과 갱신조건을 적절히 조절하여 까다로운 구간 쿼리를 해결하는 방법 중 하나입니다.

아래와 같은 문제가 있습니다.

길이 $N$의 배열 $A$, 아래와 같은 $Q$개의 쿼리가 주어진다.

• 1 L R X: 모든 $L ≤ i ≤ R$에 대해서 $A_i = min(A_i, X)$ 를 적용한다.
• 2 L R: $max(A_L, A_{L+1}, …, A_R)$을 출력한다.

// szz : tree의 size/2, i >= szz인 경우, tree[i]는 단말노드.
void propagate(int i) {
	if (i < szz) {
		for (int j : {i * 2, i * 2 + 1})
			tree[j] = min(tree[j], tree[i]);
	}
}

// 업데이트 되는 구간 : l ~ r
// tree[i]가 관리하는 구간 : le ~ ri
// max_val 해당 구간에서 가장 큰 값
void update(int i, int l, int r, int le, int ri, int X) {
	propagate(i);
	if (le > r || ri < l) return; // 중단조건(break condition)
	if (l <= le && ri <= r) {	  // 갱신조건(tag condition)
		tree[i].max_val = min(tree[i].mav_val, X);
		propagate(i);
		return;
	}
	update(i * 2, l, r, le, (le + ri) / 2, X);
	update(i * 2 + 1, l, r, (le + ri) / 2 + 1, ri, X);
	tree[i].max_val = max(tree[i * 2].max_val, tree[i * 2 + 1].max_val);
}

위 두 쿼리를 해결하는 segment tree의 update 함수 부분입니다. 위에서 말하는 중단조건과 갱신조건은 무엇을 의미할까요?

• 중단조건(break condition) : 이 구간에서 갱신되는 노드가 없음을 의미하는 조건입니다. le > r || ri < l에 해당하며 업데이트 되는 구간과 현재 노드가 관리하는 구간에서 겹치는 부분이 없으므로, 현재 노드와 그 자식 노드들 중 갱신되는 값이 없습니다.

• 갱신조건(tag condition) : 이 구간에 속한 모든 노드가 갱신되야 함을 의미하는 조건입니다. l <= le && ri <= r에 해당하며 현재 노드가 관리하는 구간이 업데이트 되는 구간에 완전히 속하므로, 현재 노드와 그 자식 노드 전부 값이 갱신되어야 합니다.

위 1번 쿼리에서 업데이트 구간에 속한 어떤 노드의 $max\space val$이 $X$이하라면, 그 구간에서 갱신되는 값이 없으므로, 중단조건을 le > r || ri < l || tree[i].max_val <= X로 변경할 수 있겠습니다. 하지만, 아직은 이것으로 얻을 수 있는 효과는 모르겠네요.

다음과 같은 구간합 쿼리를 추가로 생각해봅시다.

• 3 L R: $A_L + A_{L+1} + … + A_R$을 출력한다.

각 노드마다, 관리하는 구간의 합을 잘 관리하고 있어야 위 쿼리를 효율적으로 해결할 수 있을텐데요. 현재 갱신조건을 만족하는 부분을 업데이트 시킨다고 하더라도 업데이트 되는 $A_i$에 따라서 변경되는 가중치가 다를테니 더 엄격한 조건이 필요할 듯 합니다.

$A = [3,\space8,\space8,\space8,\space5,\space6]$에서 쿼리 1 1 6 4를 적용해봅시다.

$A = [3, \space8+(-4),\space8+(-4),\space8+(-4),\space5+(-1),\space6+(-2)]$가 됩니다.

갱신조건을 구간에 속한 값이 모두 같은 경우를 추가 조건으로 주면 구간합의 변화는 정확히 계산할 수 있습니다.

하지만, $A = [1000000,\space1,\space1000000,\space1,\space1000000,\space1,\space…, \space1000000, \space1]$과 같은 꼴일때, 1 1 N MAX_VAL-1으로 입력이 계속해서 들어오면 $O(QNlogN)$의 복잡도를 가지게 됩니다.

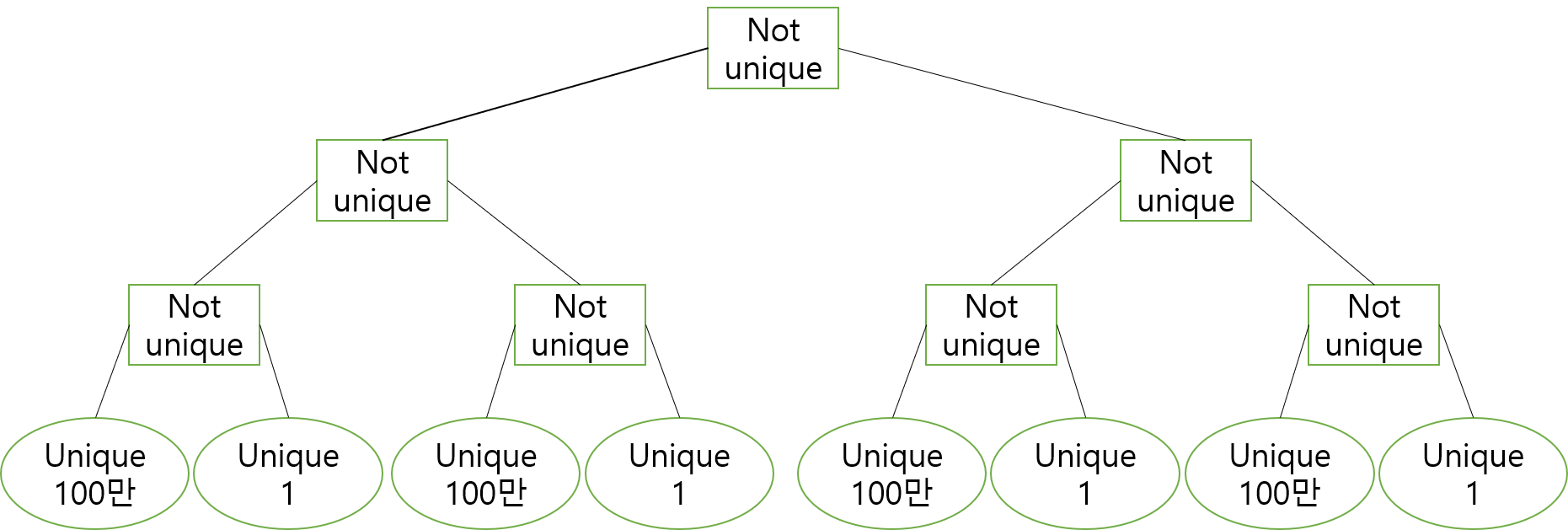
그러면 어떤 조건을 추가로 주는 것이 좋을까요? 구간에서 두번째로 큰 값을 $smax\space val$이라고 해봅시다. 여기서 두번째로 큰 값은 첫번째로 큰 값보다 엄격히 작아야 합니다.

이때, 갱신조건에서 tree[i].max_val > X && tree[i].smax_val < X를 추가로 해볼까요? 이 구간에서 $max\space val$ 값의 개수를 $max\space cnt$ 라고 할때, 이 구간의 합은 $(max\space val - X) * max\space cnt$만큼 감소하므로 구간합을 정확히 관리할 수 있습니다.

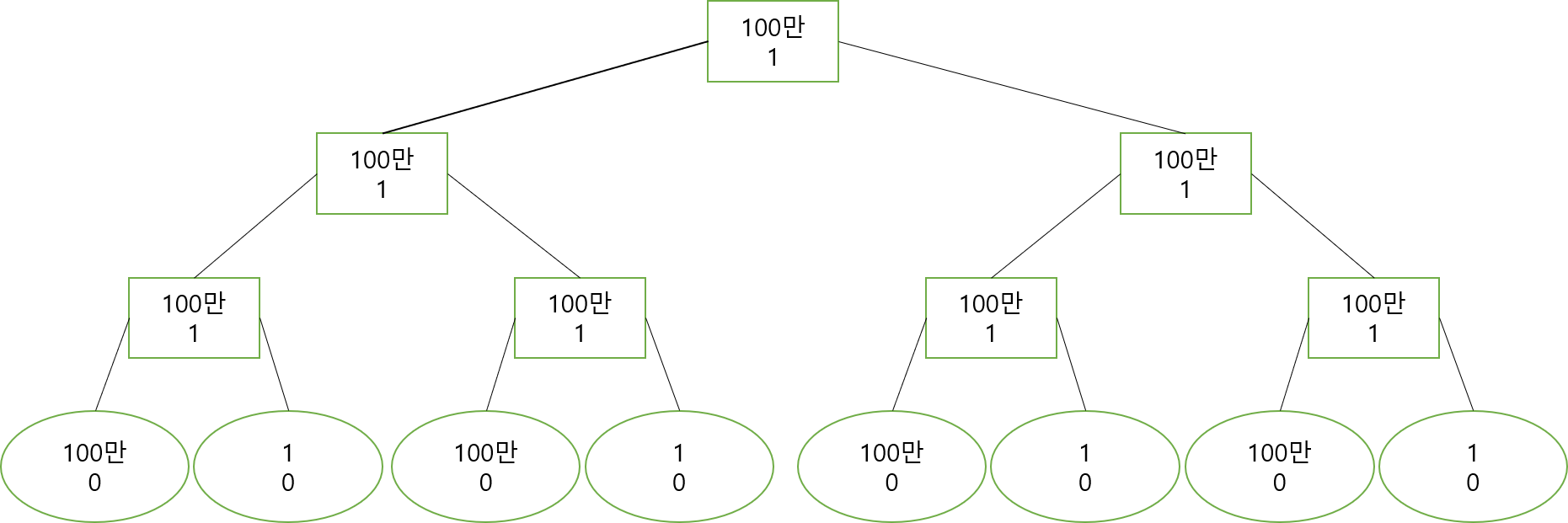
$max\space val$과 $smax\space val$로 트리를 구축한 모습입니다.

여기에 1 1 N 999999 쿼리를 보내면 어떻게 될까요?

($*$표시는 이 노드와 하위 노드의 $max\space val$이 전부 이 값의 이하라는 lazy propagation 태그입니다.)

위와 같은 예제는 루트노드만 갱신되고 나머지 propagation도 빠르게 연산되므로 쉽게 해결되겠네요.

l <= le && ri <= r && smax_val >= X인 경우가 문제되지 않을까요? 이때는, 노드의 양쪽 자식으로 분기해 내려갔을 때 $max\space val$을 가지는 노드와 $smax\space val$을 가지는 노드는 쿼리 이후 같은 값 $X$가 됩니다. 즉, 이 조건을 만족하는 경우 최소 2개의 서로 다른 노드가 같은 값을 가지게 되는 것이죠. 이 얘기는 distinct한 값의 개수가 1개이상 줄어든다는 것과 같으므로, 트리에서 위 조건을 가지는 경로를 대략 $N$번정도 지난 후에는 전부 같은 값을 가진다는 얘기가 됩니다!! 그리고 저 조건은 $smax\space val$이 존재할 때만 발생하므로 많아야 $N$번 발생하겠네요.

여기에 1 1 N 999999 쿼리를 보내면 어떻게 될까요?

서로 다른 두 값이 같은 값이 되면서 $max\space val$과 함께 $smax\space val$도 같이 업데이트 되고 있습니다.

여기에 1 1 N 999998 쿼리도 보내볼까요? 이제는 루트노드만 바꿔줘도 되겠네요.

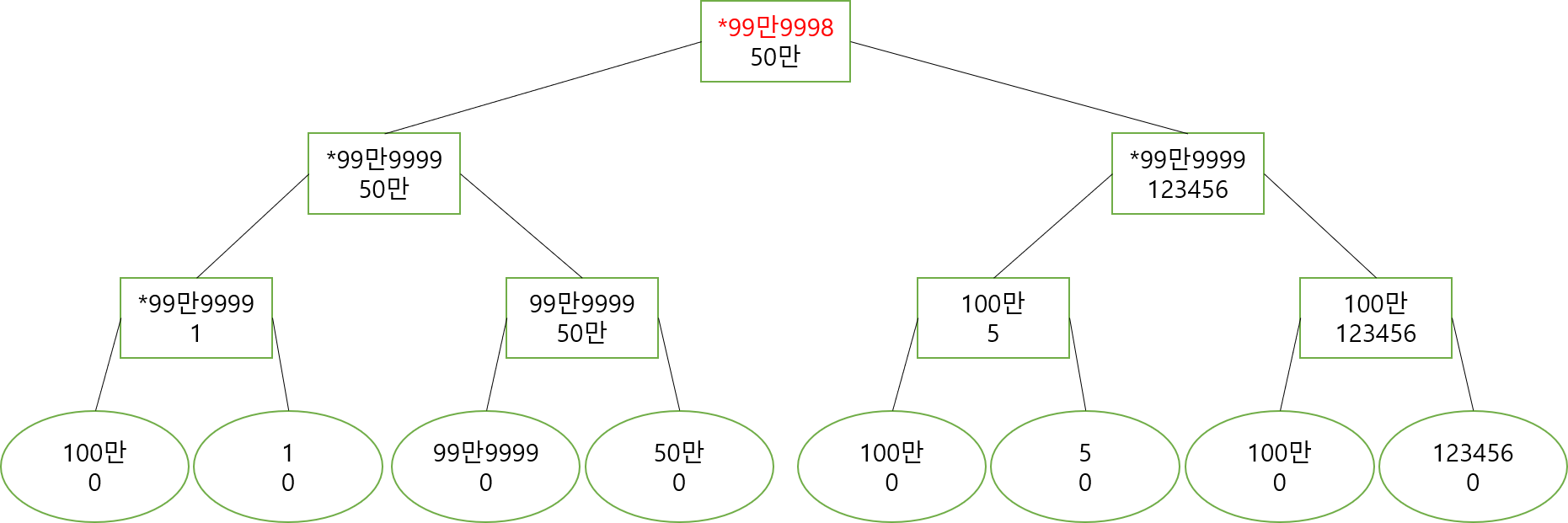
이렇게 l <= le && ri <= r && smax_val >= X조건을 만족해서 내려갈 때마다, 노드들이 합쳐지니 시간이 amortized 하게 보장이 됩니다.

이해를 위해 이렇게 적었지만, 사실은 한 번의 1 L R X 쿼리마다, $L-1$과 $L$ 그리고 $R$과 $R+1$번 위치는 각각 서로 같은 값이었다가 쿼리 이후 다른 값을 가지는 경우도 존재합니다. 따라서 약 $2Q$번정도의 다른 값이 되는 경우도 생깁니다. 그래도 $2Q$번을 더해서 최대 $N + 2Q$번만 l <= le && ri <= r && smax_val >= X인 경로를 지나가게 되므로 여전히 많지 않습니다. 위 조건을 제외하면 평범한 세그먼트 트리와 과정이 같으며, 위 조건을 가지는 경로는 많아야 $N+2Q$번 발생하고 한번 당 $O(log N)$이므로 $O((N+Q)log N)$의 시간으로 이 문제를 해결할 수 있게 됩니다.

이 로직을 작성한 코드입니다. 위에 설명한 동작과 약간 다르지만, 전체적인 역할은 동일합니다.

설명한 문제는 수열과 쿼리 26(링크) 에서 풀어보실 수 있습니다.

typedef long long ll;
struct node {
	int max_val, max_cnt, smax_val;
	ll sum;
} tree[1 << 21];

// 두 노드를 합병한 내용을 리턴
node merge(node a, node b) {
	if (a.max_val == b.max_val) return { a.max_val, a.max_cnt + b.max_cnt, max(a.smax_val, b.smax_val), a.sum + b.sum };
	if (a.max_val < b.max_val) swap(a, b);
	return { a.max_val, a.max_cnt, max(b.max_val, a.smax_val), a.sum + b.sum };
}

void propagate(int i) {
	if (i < szz) {
		for (int j : {i * 2, i * 2 + 1}) {
			if (tree[i].max_val < tree[j].max_val) {
				tree[j].sum -= (tree[j].max_val - tree[i].max_val) * (ll)tree[j].max_cnt;
				tree[j].max_val = tree[i].max_val;
			}
		}
	}
}

void update(int i, int l, int r, int le, int ri, int val) {
	propagate(i);
	if (ri < l || le > r || tree[i].max_val <= val) return;
	if (l <= le && ri <= r && val > tree[i].smax_val) {
		tree[i].sum -= (tree[i].max_val - val) * (ll)tree[i].max_cnt;
		tree[i].max_val = val;
		propagate(i);
		return;
	}

	update(i * 2, l, r, le, (le + ri) / 2, val);
	update(i * 2 + 1, l, r, (le + ri) / 2 + 1, ri, val);
	tree[i] = merge(tree[i * 2], tree[i * 2 + 1]);
}
// 구간합과 구간 최대값을 구하는 것은 다른 문제와 동일하게 적용됩니다.

그러면 세그비츠는 어떤 문제에 적용될 수 있는걸까요?

1. 구간 쿼리 문제에 사용됩니다.

2. l <= le && ri <= r을 만족하면서 갱신조건을 만족하지 않는 조건이 적게 발생해야 합니다.

   (구간에서 다른 성질(혹은 값)을 가지는 값들이 빠르게 줄어들어야 합니다.)

3. 관리해야 하는 값을 propagate와 각 조건에서 빠르게 처리할 수 있어야 합니다.

여러가지 조건이 있을 수 있겠지만, 가장 중요한 것들은 이 3가지라고 생각됩니다. 세그비츠에 대한 보다 더 자세한 설명은 https://codeforces.com/blog/entry/57319 에서 찾아보실 수 있으며, 이를 이용하는 문제는 수열과 쿼리 25~30(링크)에서 풀어보실 수 있습니다. 세그비츠를 이용한 2문제를 추가로 소개하고 글을 마치겠습니다.

수열과 쿼리 28(링크)

길이가 $N$인 수열 $A_1, A_2, …, A_N$이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오.

• 1 L R X: 모든 $L ≤ i ≤ R$에 대해서 $A_i = A_i + X$를 적용한다.
• 2 L R: 모든 $L ≤ i ≤ R$에 대해서 $A_i = ⌊√A_i⌋$를 적용한다.
• 3 L R: $A_L + A_{L+1} + … + A_R$을 출력한다.

1, 3번 쿼리는 평범한 Lazy Propagation 문제와 같습니다. 2번 쿼리는 $A_i$에 따라 변경되는 가중치가 달라서 까다롭게 느껴집니다. 하지만 제곱근 연산 특성상 값이 빠르게 감소함에 따라 같은 값이 많아집니다. 그래서 l <= le && ri <= r을 만족하면서 갱신조건을 만족하지 않는 조건이 적게 등장합니다. 구간에 존재하는 값의 sqrt한 값이 전부 같을 경우, 변경되는 가중치를 빠르게 계산할 수 있으므로 이를 갱신조건으로 주면 되겠네요. 이는 구간내의 max값과 min값의 sqrt값이 같은 지로 판별할 수 있습니다. 하지만 이런 예제를 봅시다.

$A = [10200, 10201, 10200, 10201, 10200, 10201, …]$

여기서 2 1 N, 1 1 N 10100과 쿼리가 반복해서 주어지면 같은 sqrt값으로 합쳐지지 않는데요. 이러한 예제는, 인접한 원소의 값이 1차이가 날때만 발생하므로 이에 대해 따로 처리해주면 됩니다.

// 추후 코드를 업로드 할 예정입니다.

수열과 쿼리 30(링크)

길이가 $N$인 수열 $A_1, A_2, …, A_N$이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오.

• 1 L R X: 모든 $L ≤ i ≤ R$에 대해서 $A_i = A_i ∧ X$ 를 적용한다.
• 2 L R X: 모든 $L ≤ i ≤ R$에 대해서 $A_i = A_i ∨ X$ 를 적용한다.
• 3 L R: $max(A_L, A_{L+1}, …, A_R)$을 출력한다.

먼저, 각 비트는 독립적이므로 1, 2번 쿼리를 각 비트에 대해 따로 관리하는 방법을 생각해봅시다.

1번 쿼리의 경우, $X$의 비트가 1인 부분은 아무 의미가 없고, 0인 부분만을 업데이트 해주면 됩니다.

이때, 중단조건은 le > r || ri < l || 구간에서 해당 비트가 전부 꺼짐

갱신조건은 if(l <= le && ri <= r && 구간에서 해당 비트가 전부 켜짐) {//전부 끔}으로 어렵지 않게 정할 수 있습니다.

2번 쿼리는 이와 반대로 해주면 됩니다. $X$의 비트가 0인 부분은 아무 의미가 없고, 1인 부분만을 업데이트 합니다.

이때, 중단조건은 le > r || ri < l || 구간에서 해당 비트가 전부 켜짐

갱신조건은 if(l <= le && ri <= r && 구간에서 해당 비트가 전부 꺼짐) {//전부 켬}이 됩니다.

이러면 이 문제를 $O((N+Q)Log^2 N)$에 해결할 수 있습니다만, 이 시간복잡도로 제한 2초에 맞추는 것이 어렵습니다. 이를 $O((N+Q)Log N)$에 해결해볼까요?

최적화 방식으로 구간에서 전부 켜져 있거나, 전부 꺼져있는 특정 비트들을 함께 갱신해주는 것을 생각해봅시다. 이 처리를 하나의 propagate 혹은 갱신과정을 $O(1)$에 할 수 있습니다. 하나의 update쿼리에서 $Log$개의 각 비트당 최대 2개의 다른 값이 생기니 여전히 $Log^2N$이라고 생각이 될 수도 있습니다. 하지만 놀랍게도 이 방법의 복잡도는 $O((N+Q)Log N)$가 됩니다. 각 비트당 최대 2개의 다른 값이 생기는 변화는 L~R 구간 업데이트 시 같은 위치에서 발생되며 다른 쿼리에서 동시에 처리될 것이기 때문입니다. 따라서 이를 아래 코드와 같이 구현할 수 있습니다.

int max_val[1 << 19];
int one[1 << 19]; // 구간에서 전부 1인 bit만 켜져 있음
int zer[1 << 19]; // 구간에서 전부 0인 bit만 켜져 있음.
int al[1 << 19]; // and lazy, 켜진 비트 부분이 전부 0이 되어야 한다.
int ol[1 << 19]; // or lazy, 켜진 비트 부분이 전부 1이 되어야 한다.

void propagate(int i) {
	max_val[i] |= ol[i];
	one[i] |= ol[i];
	zer[i] -= zer[i] & ol[i];

	max_val[i] &= ~al[i];
	one[i] -= one[i] & al[i];
	zer[i] |= al[i];

	if (i < szz) {
		for (int j : {i * 2, i * 2 + 1}) {
			ol[j] &= ~al[i];
			al[j] &= ~ol[i];

			ol[j] |= ol[i];
			al[j] |= al[i];
		}
	}
	ol[i] = al[i] = 0;
}

void ad(int i, int l, int r, int le, int ri, int val) {
	propagate(i);
	if (le > r || ri < l) return;
	val -= zer[i] & val;
	if (l <= le && ri <= r && (val & one[i])) {
		al[i] = val & one[i];
		val -= val & one[i];
		propagate(i);
	}

	if (val == 0) return;
	ad(i * 2, l, r, le, (le + ri) / 2, val);
	ad(i * 2 + 1, l, r, (le + ri) / 2 + 1, ri, val);
	one[i] = one[i * 2] & one[i * 2 + 1];
	zer[i] = zer[i * 2] & zer[i * 2 + 1];
	max_val[i] = max(max_val[i * 2], max_val[i * 2 + 1]);
}

void od(int i, int l, int r, int le, int ri, int val) {
	propagate(i);
	if (le > r || ri < l) return;
	val -= one[i] & val;
	if (l <= le && ri <= r && (val & zer[i])) {
		ol[i] = val & zer[i];
		val -= val & zer[i];
		propagate(i);
	}

	if (val == 0) return;
	od(i * 2, l, r, le, (le + ri) / 2, val);
	od(i * 2 + 1, l, r, (le + ri) / 2 + 1, ri, val);
	one[i] = one[i * 2] & one[i * 2 + 1];
	zer[i] = zer[i * 2] & zer[i * 2 + 1];
	max_val[i] = max(max_val[i * 2], max_val[i * 2 + 1]);
}

마치며

궁금하신 점이나 잘못된 부분이 있다면, 제 블로그(링크)계정을 통해 전달하실 수 있습니다.

긴 글 읽어주셔서 감사합니다.