Flow with demands
목차
개요
이번에 소개할 알고리즘은 Flow with demands 입니다. 보통의 간선에 흐를 수 있는 유량에 상한이 있는 최대 유량 문제와 다르게 하한이 있는 최대 유량 문제를 효과적으로 해결하는 알고리즘 이며, 2016년도 한국 ACM-ICPC 예선 H번에서 이 알고리즘을 사용하게 됩니다. 기본적인 아이디어와 작동원리 등을 설명하고 실제로 문제풀이에 어디에 쓰이는지 보이고자 합니다. 일단 기본적으로 최대 유량에 대한 기본 지식이 있어야 하며, Sink, Source 등의 용어등에서도 잘 알고 있어야 이 포스트를 읽을 수 있습니다.
Demands(수요)가 대체 뭐야?
Flow 면 Flow 지 갑자기 Demands(수요)가 나타나서 당황스러울 것 입니다. 이 Demands 가 매우 중요한 포인트인데요, Flow with demands 에서 demands 는 다음과 같이 정의 됩니다.
여러개의 Sink 가 있다고 가정할 때, 해당 Sink로 흘려보내야 하는 유량의 크기
이는 보통 $d_{x}$로 나타내며, $x$는 vertex를 나타내며, $d_{x}$는 해당 vertex 의 demands 를 의미합니다. 음, 농담삼아 경제학을 공부한 사람이라면(물론 저는 아닙니다.), 수요가 있으면 공급도 있어야지! 라고 생각할 수 있는데요. 네, 당연하게도 공급이 있습니다. 이를 Supplies 라고 하며, Demands의 반대 개념으로 쓰입니다만, 우리가 해결하고자 하는 문제에서는 Demands 로 모두 퉁치게 됩니다. 하지만 여기서 Supplies 는 다음과 같이 정의합니다.
$d_{x} < 0$ 인 모든 Demands를 Supplies 라고 한다.
즉, Demands 값이 0보다 작은 값들은 모두 공급이라고 부르게 됩니다. Demands 로 모두 통일하여 부르기 위해, 그리고 코딩의 편리함을 위해 다음과 같이 관리하게 됩니다. 수요가 음수, 즉, “나는 필요없으니까 너 가져.” 같은 느낌으로 설명하면 쉽게 이해가 되려나요?
그렇다면 우리는 이러한 정의가 내려져 있는 수요가 있는 최대 유량 문제를 해결하고자 합니다.
Flow with demands 해결법
네 그러면 바로 이 문제를 해결하기 위해 다음과 같은 그래프를 그릴 것 입니다.
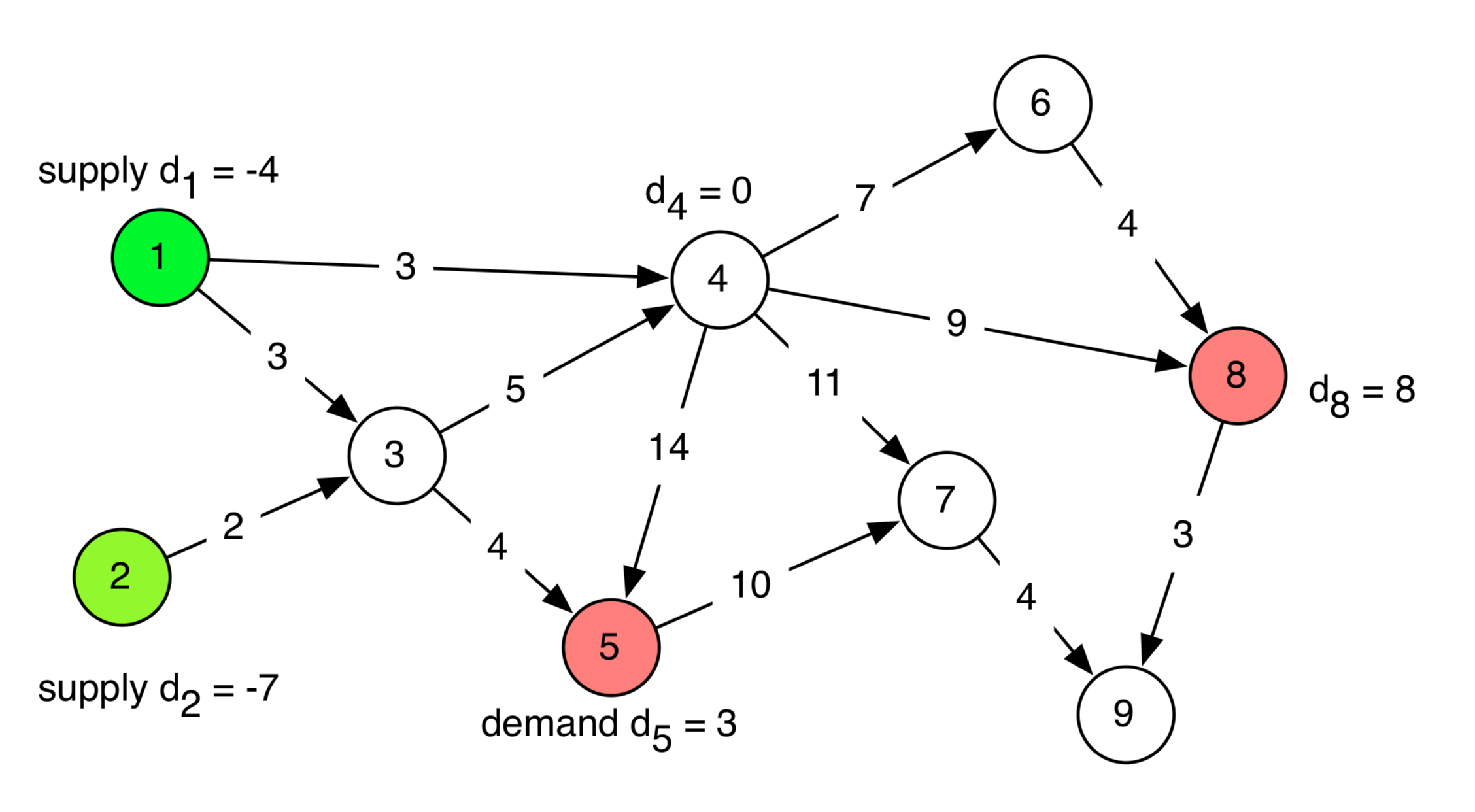
우선 1번 정점과, 2번 정점에서 각각 4, 7의 공급이 이루어지고 있습니다. 또한 이를 demands 로 나타내어 -4, -7로 나타내고 있습니다. 그리고 5번 정점과, 8번 정점에서 각각 3, 8의 수요를 요구하고 있습니다. 또한 이를 demands 로 나타내어 3, 8로 나타내고 있습니다.
자 그렇다면 여기에서, 최대한 많은 유량을 흘려보내면서 저러한 수요를 요구하는 노드로 유량을 흘려보내려면 어떻게 해야할까요? 네, 유량문제에 대한 모델링을 여러번 경험해본 사람이라면 바로 결론을 내릴 것 입니다. 여러개의 Source 정점이 있으므로 이를 한개의 Source 처럼 활용 할 수 있도록, 가상의 Source 정점 $s’$를 만드는 것 입니다. 그리고 Sink 역시 여러개 이므로 이를 한개로 취급할 가상의 Sink 정점 $t’$을 만드는 것 입니다. 이후 $s’$에서 Supplies 로 흐르는 간선들을 만들어줍니다. 예를 들어 $s’$에서 1번 정점으로 상한이 4인 간선을 만들어주고, $s’$에서 2번 정점으로 상한이 7인 간선을 만드는 것입니다. 그리고 나서 $t’$로 향하게끔 값이 0보다 큰 demands 들을 연결해주면 끝입니다. 예를 들어, 5번 정점에서 $t’$으로 상한이 3인 간선을 만들어주고, 8번 정점에서 $t’$으로 상한이 8인 간선을 만들어 주면 됩니다. 얼추 모델링이 되시나요?
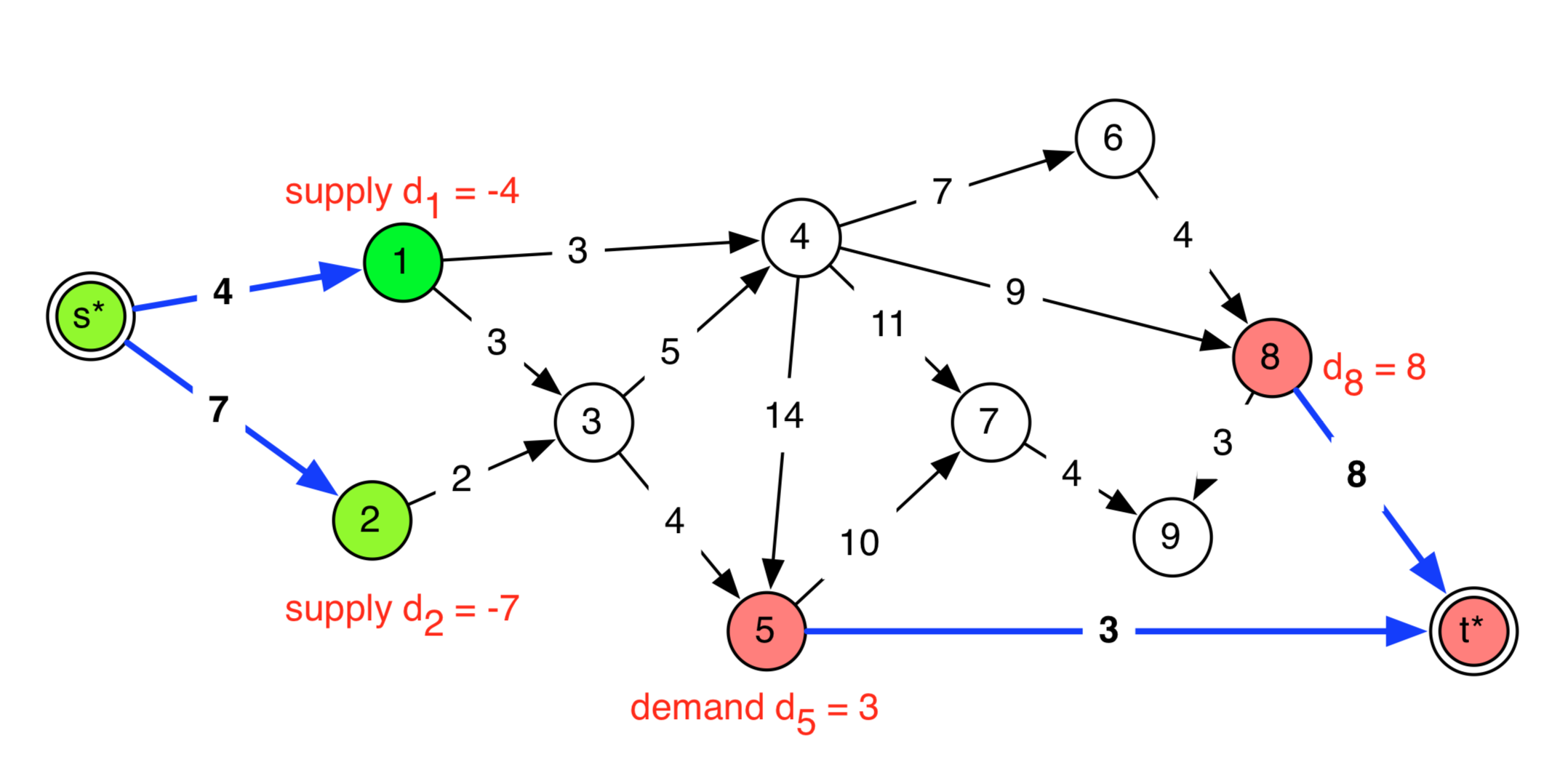
완성된 그래프 $G’$은 다음과 같이 나오며, 여기에서 Flow 문제를 해결하면 정말 당연하게도 풀립니다. 정당성에 대한 증명은 여러분에게 맡기겠습니다.
응용
하지만 여기서 끝이 아닙니다. 고작 이런 문제를 풀고자 이 포스를 쓴것이라면, 최대 유량을 설명하면서 같이 끼워넣는 수준으로 끝났을 쉬울 내용입니다. 지금부터 다루고자 하는 것은 저 아이디어를 가져와서 하한이 있는 유량 문제를 해결하는 것 입니다.
하한, Lower bound 라고 많이 부르며, 일반적인 최대 유량 문제는 상한, 즉, Upper bound 를 다룹니다. 흐를 수 있는 양을 제한 하는 것과 달리 반드시 이 간선에 특정 값 이상 반드시 유량이 흘러야 되는걸 보장해야 하는 문제를 해결할 때 쓰이게 됩니다.
우선 특정 간선에 대해 $e(u, v)$ 라고 합시다. 이를 짧게 해서 그냥 $e$ 라고 나타냅시다. 여기에서 $l_{e}$ 를 그 간선에 대한 하한 이라고 합시다. $c_{e}$ 를 그 간선에 대한 상한, 혹은 capacity 라고 합시다. 또한 우리는 demands 가 발생하는 조건을 다음과 같이 정의 할 것 입니다. 정점을 $v$라고 하고 flow 가 해당 정점에 들어오는 것은 $f_{in}(v)$ 나가는 것을 $f_{out}(v)$ 이라고 합시다. 이때 $d_{v}$는 $f_{in}(v) - f_{out}(v)$가 됩니다. 대충 어떤 느낌인지 감이 오시나요? 네, 감이 잘 오지 않을텐데 다음과 같은 상황을 상정해 봅시다. 예를 들어 $l_{e} = 4$ 이고 $e(2, 4)$ 라고 가정해봅시다. 즉 2번 정점에서 4번 정점으로 4가 최소한 흘러야 되는 상황인 것입니다. 이때, 2번 정점에서 4만큼 흘려보내려면 2번 정점은 4 만큼이 들어와야, 즉, demands 가 0인 상태라면 4 만큼을 더 요구해야 되는 상황인 것입니다. 이는 $f_{in}(2)$가 4인 상황인 것 입니다. 또한 4번 정점의 경우 4 를 받았으므로 4를 내보낼 수 있는 상황, 즉 $f_{out}(4)$ 가 4인 상황인 것 입니다. 즉, 이때는 2번은 4만큼 필요하니 $d_{2} = 4$, 4번은 4만큼 내보낼 수 있으니 $d_{4} = -4$가 되겠네요. 그렇다면 여기서 남은것은 $l_{e}$ 에 대한 값에 대한 처리입니다. 우리가 $e(u, v)$ 에 대해 $l(e)$ 가 0보다 큰 상황이 존재할 때, $d_{u}$ 에는 $l(e)$ 만큼 더해주고, $d_{v}$ 에는 $l(e)$ 만큼 빼줬는데요, 이때의 $c(e)$ 는 어떻게 해줘야할까요?
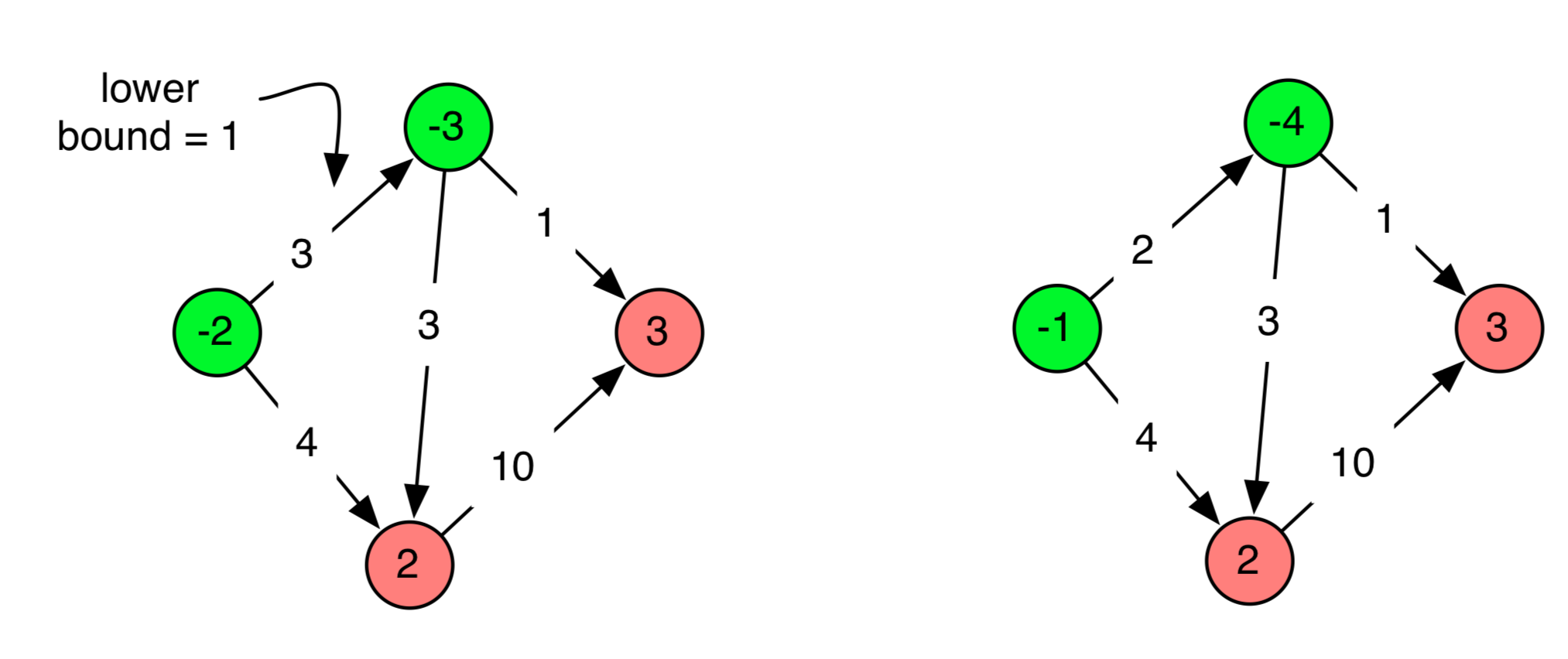
네 답은 간단합니다. $c(e)$에 $l(e)$ 만큼 빼주면 됩니다. 내가 그 간선에 대해 $l(e)$ 만큼 썼다는걸 보장하는 것이지요. 그렇다면 이것이 정당할까요? 네, 정당합니다. 모든 demands 가 0 인 상황을 가정하고, 내가 특정 demands 들을 모두 만족한다면은 그 간선에 $l(e)$ 만큼을 흘려보낼 수 있다는 것은 매우 자명한 사실입니다. 이러한 프로세스를 모든 $e \include E$의 $l(e)$에 대해 모두 진행한 뒤에 그래프에서 flow를 실행하면 간단하게 해결 될 것 입니다.
하지만, 아직 끝나지 않았습니다. 위 그림에서는 수요와 공급이 이미 주어진 상황에서 lower_bound가 추가되어있는 상황입니다. 이 상황이 아닌 일반적인 상황 이미 source와 sink가 주어져있는 유량 문제 상황에서, 즉, demands 가 존재하지 않는 상황에서 간선의 lower_bound 만 결정되어있는 상황이라고 생각해봅시다. 물론 우리는 위에서 설명한 프로세스로 모든 정점들의 demands 를 결정한다음 가상의 source와 가상의 sink를 만들어서 해결하려 할 것 입니다. 거기에 자연스럽게 source 에 매우매우 큰 수, 대충 1억정도로 생각할까요? 아무튼 그 수를 빼주고 sink에 매우매우 큰 수를 더해서 기존의 source sink 규칙을 만족한 상황에서 flow 를 돌리면 될것이다. 정도는 여기까지 제 포스트를 열심히 읽으신 분이라면 전부 떠올리셨을 것이고, 바로 그러한 문제들을 해결하러 가셨을 것 입니다. 하지만 제가 이렇게 말을 길게 끄는 이유는 우리는 그렇게 흘려보낸 flow 가 실제로 모든 lower_bound를 만족하는 flow 인지 검증할 방법이 없다는 것을 바로 눈치 챌 수 있습니다. 그렇다면 어떻게 검증할까요?
그 방법은 매우 간단합니다. 기본적으로 Max Flow 를 구하는 것이 목표가 아니라면, 즉, 모든 lower_bound 만 만족하는게 목표라면 원래의 sink 에서 원래의 source로 매우 큰 capacity 를 가진 flow 를 연결해주면 해결 됩니다. 그리고 위에서 설명한 매우 큰 수를 source의 demands 에는 빼고 sink의 demands 에선 더하는 것을 하지 않은 상태에서 모든 양의 정수의 demands들을 더한 값 보다 flow가 작으면 불가능한 것, 같으면 가능한 것 입니다. 즉, $e(t, s)$ 를 생성하고 $c(e)$를 매우 큰 숫자로 잡는것입니다. 이것이 왜 정당할까요? 이는 매우 간단하게 설명하면 다음과 같습니다. $e(u, v)$ 가 있고, 이것에 대한 $l(e)$ 가 존재한다고 가정해 봅시다. 이때, 그래프 재구축이 일어나기 전에 플로우 경로는 s - … - u - v - … - t 가 될것입니다. 하지만, u에서 일정량을 더 흘려보냈으니, 반드시 흘려보내야 하는 규칙이 생겼으니, u - t’와 s’ - v 두개의 경로가 생길것입니다. 하지만 이 경우 그러한 경로를 보장하지 못하지만, 만약 우리가 여기서 $e(t, s)$에 대한 경로를 생성한다면 s’ - v - … - t - s - … - u - t’ 의 경로가 발생하여 완벽하게 연결이 됩니다! 좀 더 엄밀한 증명은 여러분에게 숙제로 남겨두겠습니다.
자 그러면 max flow 와, 검증 두가지를 모두 실행하려면 그래프를 두개 마련해놨다가 검증 용 t-s 경로가 추가된 그래프와 s의 demand에 매우 큰수를 빼고 t의 demand에 매우 큰수를 더한 그래프 두개로 나눈 뒤, 각각에서 flow를 구하면 해결 되겠죠?
문제풀이
2016년도 한국 ACM-ICPC 예선 H번문제를 같이 풀어볼 것 입니다. 이 문제는 일하는 노동자가 있는데, 최소한 $p$일은 일해야 하고, $p’$ 일 보다 초과하여 일하면 안됩니다. 총 $n$일 동안 작업이 펼쳐지는데 각 날짜에는 최소 일해야 하는 인원수와 최대 일해야하는 인원수가 주어집니다. 마지막으로 각 직원은 특정 기간동안 며칠동안 쉬고 싶은것에 대한 리스트를 작성하여 저희들에게 넘겨줬는데요, 저희는 그들을 위해 모든 조건을 만족하면서 그들이 언제 쉬어야할지 결정하는 알고리즘을 작성해야 합니다. 당연하게도 이는 Flow with demands 로 해결할 수 있습니다. 먼저 쉬어야 한다에 초점을 맞춰야 하므로 $n-p’$ 일 만큼은 쉬어야 하고, $n-p$ 일 보다 많이 쉬면 안된다. 로 변형할 수 있습니다. 이를 각각 lower bound와 capacity 로 해석하여 사람을 정점으로 만들고 간선을 생성 할 수 있습니다. 여기에서, 각 사람이 쉬고싶은 기간을 정점으로 만들어주고 그 정점에서 최소 쉬어야 하는 일수 를 lower_bound로 그 기간의 길이를 capacity 로 하면 또 간선을 생성해 줄 수 있습니다. 그리고 각 기간에 대해 그 기간에 속하는 모든 일수에 lower_bound는 0으로 capacity 는 1로 edge를 만들어 주면 해결입니다. 마지막으로, 각 날짜 $i$에 대해 일해야 되는 최소 인원수를 $q_{i}$ 최대 인원수를 $q’{i}$ 라고 할 때, $n-q’{i}$로 쉬어야 하는 최소 인원수, $n-q_{i}$로 쉬어야 하는 최대 인원수로 고치게 되면 간선을 만들어 줄 수 있게 됩니다. 이렇게 완성된 그래프에서 위의 응용을 이용해서, 새로운 그래프를 구축하고 flow를 실행하면 (Dinic, Edmonds-Karp, Ford-Fulkerson …etc) 우리가 그렇게 쉬는 사람을 배정할 수 있을지 찾을 수 있게됩니다. 물론 우리는 가능한 많은 사람을 쉬게 해줘야 한다는 조건은 없으므로, 가능한지 여부에 대한 체크, 즉, Flow를 단 한번만 돌리면 해결 할 수 있습니다.
int src = 0, sink = 1;
int tmp1 = p1;
int tmp2 = p2;
p1 = n - tmp2;
p2 = n - tmp1;
for(int i = 2; i <= m + 1; i++) {
add_edge(src, i, p2 - p1);
demands[src] += p1;
demands[i] -= p1;
}
for(int i = m + 2; i <= n + m + 1; i++) {
int x, y;
scanf("%d %d", &x, &y);
int tmx = x;
int tmy = y;
x = m - tmy;
y = m - tmx;
add_edge(i, sink, y - x);
demands[i] += x;
demands[sink] -= x;
}
먼저 기존의 소스와 싱크를 0, 1 로 두고 위에서 언급했던 사람을 정점으로 만들고 날짜를 정점으로 만들어서 간선을 추가하는 과정입니다. demands 부분과 add_edge에서 lower bound의 처리 부분을 확인해주세요.
int sum = 0;
for(int i = 2; i <= m + 1; i++) {
int k;
scanf("%d", &k);
st_p[i] = n + m + 2 + sum;
ed_p[i] = n + m + 2 + sum + k - 1;
for(int j = n + m + 2 + sum; j <= n + m + 2 + sum + k - 1; j++) {
int d, x, y;
scanf("%d %d %d", &d, &x, &y);
add_edge(i, j, (y - x + 1) - d);
demands[i] += d;
demands[j] -= d;
for(int l = m + x + 1; l <= m + y + 1; l++) {
add_edge(j, l, 1);
demands[j] += 0;
demands[l] -= 0;
}
}
sum += k;
}
기간을 정점으로 만들고 그 기간에 연결된 날짜수에 간선을 추가해주는 작업입니다. 위의 설명과 한번 비교해보세요.
N = n + m + 2 + sum + 2;
s = n + m + 2 + sum;
t = n + m + 2 + sum + 1;
int goal = 0;
for(int i = 0; i < N - 2; i++) {
if(demands[i] < 0) add_edge(s, i, -demands[i]);
if(demands[i] > 0) add_edge(i, t, demands[i]);
}
add_edge(sink, src, 1e8);
for(int i = 0; i < N; i++) if(demands[i] > 0) goal += demands[i];
if(dinic() < goal) {
printf("-1\n");
return 0;
}
마지막으로 demands 에 따라 새로 생길 소스와 싱크를 연결하고(s, t) 원래 싱크에서 원래 소스로 매우 큰 수를 카파시티로 하는 간선을 생성하는 부분을 주의깊게 봐주세요.(sink, src) 그 다음 demands가 양의 정수라면 모두 더해둬서 실패하는 경우를 찾는 데 사용합니다. 위의 설명과 비교해보세요.
printf("1\n");
for(int i = 2; i <= m + 1; i++) {
int sum = 0;
for(int j = st_p[i]; j <= ed_p[i]; j++) {
for(auto &v : g[j]) {
auto &x = e[v];
if(m + 2 <= x.b && x.b <= n + m + 1 && x.flow) {
sum++;
}
}
}
printf("%d ", sum);
for(int j = st_p[i]; j <= ed_p[i]; j++) {
for(auto &v : g[j]) {
auto &x = e[v];
if(m + 2 <= x.b && x.b <= n + m + 1 && x.flow) {
printf("%d ", x.b - m - 1);
}
}
}
printf("\n");
}
마지막은 일반적인 유량 문제를 많이 해결해보신 분이라면 많이 보셨을 과정입니다. 내가 사용한 (기간-날짜) 간선을 체크해서 특정 사람이 어떤날에 쉬어야 되는지 결정해서 출력합니다.
마무리
Flow with demands 는 매우 쉬운 개념이며, 누구나 해결할 수 있지만, 그것에 대해 한국어로 자세하게 서술한 블로그가 많이 없어서, 제가 직접 해보았습니다. 부족한 글솜씨고, 오히려 이해를 해칠수도 있어서 참고자료에 들어가서 공부하는것이 더욱 도움이 될지도 모르겠지만, 저의 포스트를 읽고 알고리즘 공부에 조금이라도 도움이 된 사람이 있었으면 좋겠다고 생각하며, 이 포스트를 마무리 짓겠습니다. 감사합니다.