Knuth's Algorithm X
안녕하세요?
오늘은 Knuth’s Algorithm X에 대해 알아보도록 하겠습니다. Knuth’s Algorithm X는 기본적으로 Brute-Force 알고리즘의 일종이지만, 성능이 좋은 편에 속하고 그 과정이 상당히 아름답습니다.
Knuth’s Algorithm X
Knuth’s Algorithm X는 간단히 말해, 어떠한 집합의 exact cover를 찾는 알고리즘입니다. Exact cover란 무엇인지, 간단한 예시를 통해 살펴보도록 하겠습니다.
집합 X = {1, 2, 3, 4, 5, 6, 7}이 있고, 집합 X의 부분집합의 집합인 집합 S가 주어집니다.
S = {A, B, C, D, E, F}라고 하고 각각을 다음과 같이 정의해봅시다.
A = {3, 5, 6}
B = {1, 4, 7}
C = {2, 3, 6}
D = {1, 4}
E = {2, 7}
F = {4, 5, 7}
이 때, 다음 두 가지 조건을 만족하는 S의 부분집합을 exact cover라 합니다.
i) 고른 원소들이 모두 distinct해야 한다.
ii) 고른 원소들의 합집합이 집합 X가 되어야 한다.
위 예시에서는 세 원소 A, D, E를 고른다면 위 조건을 만족합니다. 하지만 일반적으로 이러한 exact cover을 구하는 것은 안타깝게도 NP문제에 속합니다.
Knuth는 이러한 exact cover을 찾는 알고리즘을 고안하였는데, 다음과 같이 작동합니다. 편의상 아까의 예시를 다음과 같은 행렬로 나타내도록 하겠습니다.
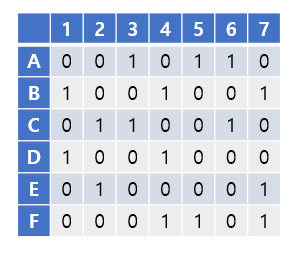
-
만약 행렬이 비어있다면, 성공적인 답안을 찾아낸 것이므로 답을 출력하고 return한다.
-
1의 개수가 가장 적은 column을 하나 고른다.
2-1. column에 1이 하나도 없다면 답이 존재하지 않으므로 return한다.
-
고른 column에서, 1이 속해있는 row를 하나 고른다. (nondeterministically)
-
2번에서 고른 row와, row에 있는 1들이 속해있는 column을 삭제한다.
-
3번에서 삭제되는 column에 있는 1들이 속해있는 row를 삭제한다.
-
1번부터의 과정을 반복한다.
말로는 이해가 쉽지 않을 수 있습니다. 예시를 통해 다시 한 번 살펴보겠습니다.
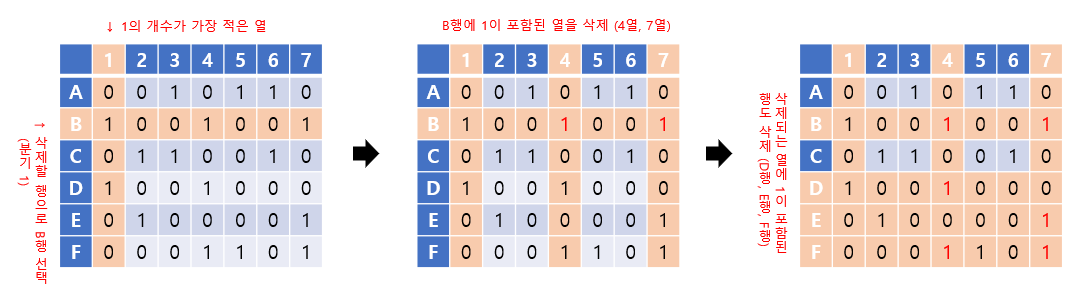
가장 먼저 1의 갯수가 가장 적은 1열을 선택하고, 이 중 B행을 선택합니다. B행을 선택하는 부분은 nondeterministically한 과정이므로 이곳을 분기 1로 합니다.
B행에 1이 포함된 4, 7열을 삭제하고, 4열과 7열에 1이 포함된 D, E, F행도 삭제합니다.
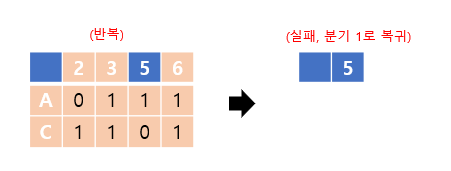
마찬가지 과정을 반복하면, 5열에 1이 하나도 없게 되므로 실패합니다. 따라서 분기 1로 되돌아갑니다.
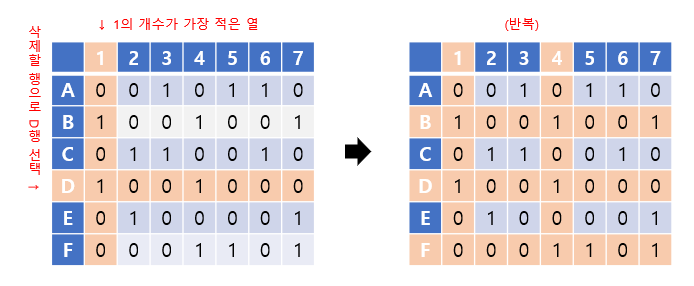

D행을 선택한 뒤 마찬가지 과정을 반복하면, 최종적으로 빈 행렬이 만들어지므로 정확한 exact cover을 찾는 데에 성공하게 되었습니다.
Knuth’s Algorithm X는 알고리즘 자체는 굉장히 간단합니다.
곰곰이 생각해보면, 사실 Knuth’s Algorithm X는 일반적으로 생각할 수 있는 Brute-Force와 크게 달라 보이지 않습니다. 그렇다면 굳이 Knuth’s Algorithm X를 사용해야 할 이유는 무엇일까요?
이는 Knuth’s algorithm X는 바로 다음에 소개할 Dancing Link라는 기법을 사용하기에 굉장히 적합하기 때문입니다.
Dancing Link를 이용해 구현된 Knuth’s algorithm X를 DLX라고 부르기도 합니다.
Dancing Link
Linked list라는 자료 구조는 굉장히 흔하게 사용됩니다.
이를 2차원으로 확장하여 위, 아래, 왼쪽, 아래쪽으로 연결된 4방향의 Linked list도 그리 특별하지 않게 널리 사용되는 편입니다.
이 Linked list는 삭제를 $O(1)$에 할 수 있다는 크나큰 장점이 있는데,
this->left->right = this->right;
this->right->left = this->left;
의 두 줄로 가능합니다. (2차원이라면 위아래까지 진행해야 합니다)
그렇다면 이렇게 삭제한 노드를 다시 삽입할 수 있을까요? 사실 위와 거의 동일하게, $O(1)$에 처리 가능합니다.
this->left->right = this;
this->right->left = this;
다만 이렇게 노드를 추가할 경우, 삭제가 어떻게 진행되냐에 따라 오류가 발생할 수 있습니다. 가령 노드 x가 삭제되고, r[x]가 삭제되고 다시 x를 추가하려 하면 오류가 발생하겠지요.
하지만 노드의 삭제와 추가의 순서가 잘 보장된다면(가장 최근에 삭제된 노드부터 다시 추가된다면), 위 방법을 사용해도 문제가 없습니다. 그리고 Knuth’s algorithm X는 그 순서가 잘 보장됩니다.
이제 앞에서 예시로 사용했던 행렬을 Linked list 형태로 나타내보겠습니다.
가장 먼저, head를 하나 만들어야 합니다. 이 head는 각각의 column들의 head와 연결되어 있습니다.
각 column들의 head는 해당 column에 포함된 1과 연결되어 있으며, 같은 row에 있는 1끼리도 연결되어 있습니다.
최종적으로 다음 그림과 같은 형태를 띠게 됩니다.
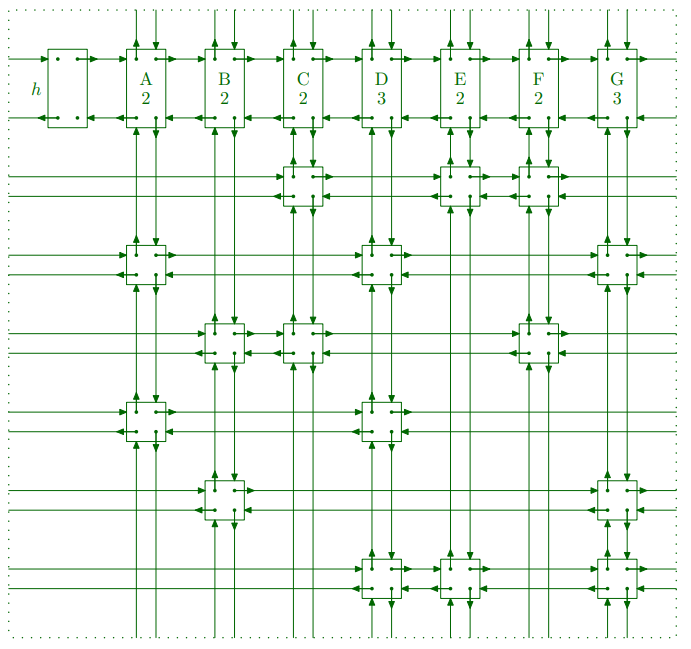
코드로는 다음과 같이 나타낼 수 있습니다.
struct node {
int row;
int size;
node* column;
node* up;
node* down;
node* left;
node* right;
};
up, down, left, right는 각 방향의 노드를 가리킵니다.
size는 header node에서 사용되는 것으로, 해당 column에 있는 1의 갯수를 셉니다.
row는 노드의 열 번호를 저장해놓은 것으로, 정답을 출력할 때 사용합니다.
마지막으로 column은 해당 노드의 column header를 가리킵니다.
Knuth’s algorithm X를 진행할 때 한 column을 삭제했던 것은 cover라는 operation으로 대체할 수 있습니다.
한 column을 cover하면, 해당 column의 head를 삭제하고, 해당 column의 노드들과 같은 row에 있는 노드들의 위아래 연결을 해제하게 됩니다. 예컨대 column A를 cover하면 다음과 같은 형태로 바뀌게 됩니다.
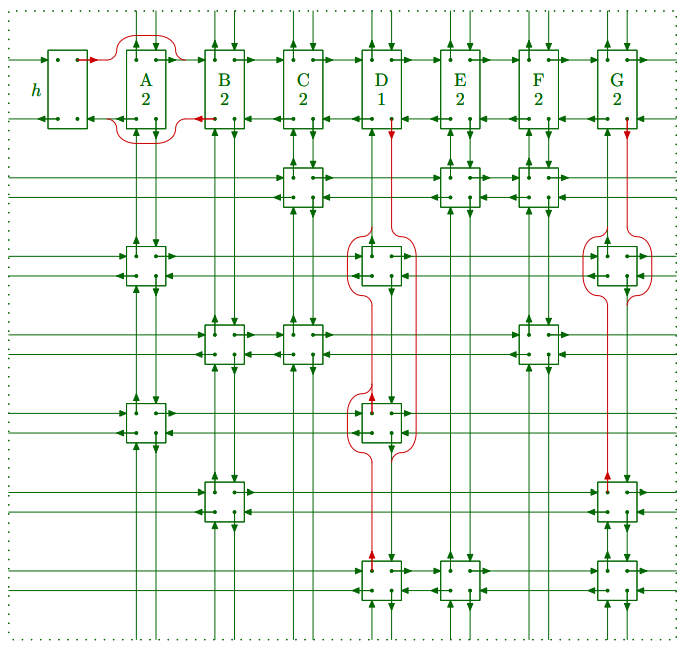
코드로는 다음과 같이 나타낼 수 있습니다.
void dlx_cover(node* c) {
c->right->left = c->left;
c->left->right = c->right;
for (node* it = c->down; it != c; it = it->down) {
for (node* jt = it->right; jt != it; jt = jt->right) {
jt->down->up = jt->up;
jt->up->down = jt->down;
jt->column->size--;
}
}
}
위에서 사용했던 예시에서, 답이 존재하지 않을경우 분기로 다시 되돌아갔던 것을 기억하실겁니다. 되돌아가려면 cover했던 column들을 다시 uncover해야 하는데, 위 과정을 반대로 진행하는 것만으로 간단하게 해결할 수 있습니다.
void dlx_uncover(node* c) {
for (node* it = c->up; it != c; it = it->up) {
for (node* jt = it->left; jt != it; jt = jt->left) {
jt->down->up = jt;
jt->up->down = jt;
jt->column->size++;
}
}
c->right->left = c;
c->left->right = c;
}
최종적인 Kunth’s algorithm X의 코드는 다음과 같습니다.
bool dlx_search(node* head, int k, vector<int>& solution) {
if (head->right == head) return 1;
node* ptr = nullptr;
int low = INF;
for (node* it = head->right; it != head; it = it->right) {
if (it->size < low) {
if (it->size == 0) return 0;
low = it->size;
ptr = it;
}
}
dlx_cover(ptr);
for (node* it = ptr->down; it != ptr; it = it->down) {
solution.push_back(it->row);
for (node* jt = it->right; jt != it; jt = jt->right) {
dlx_cover(jt->column);
}
if (dlx_search(head, k + 1, solution)) return 1;
else {
solution.pop_back();
for (node* jt = it->left; jt != it; jt = jt->left) {
dlx_uncover(jt->column);
}
}
}
dlx_uncover(ptr);
return 0;
}
위 코드에서 low를 찾는 부분, 즉 가장 원소의 갯수가 적은 column을 찾는 부분은 해당 상태에 존재하는 모든 column을 방문해야 하기 때문에 시간이 오래 걸릴 수 있습니다.
물론 원소가 가장 적은 column을 굳이 찾지 않고, 아무 column이나 선택해서 진행해도 최종적으로는 정당한 답을 찾을 수 있습니다. 각 column마다 1이 몇 개 포함되어 있는지 size를 저장하고 업데이트할 필요도 없게 되므로 실행 속도 또한 빨라지게 됩니다.
하지만 실험적으로, 가장 원소의 갯수가 적은 column을 찾아서 진행하는 것이 평균적인 실행시간이 더 빠르다고 알려져 있습니다. 자세한 설명은 논문을 참고하시기 바랍니다.
마지막으로 input으로 행렬이 들어왔을 때, 이를 four-way linked list 형태로 바꾸어주는 부분의 코드는 다음과 같습니다.
vector<int> dlx_solve(vector<vector<int>> matrix) {
int n = matrix[0].size();
vector<node> column(n);
node head;
head.right = &column[0];
head.left = &column[n - 1];
for (int i = 0; i < n; ++i) {
column[i].size = 0;
column[i].up = &column[i];
column[i].down = &column[i];
if (i == 0) column[i].left = &head;
else column[i].left = &column[i - 1];
if (i == n - 1) column[i].right = &head;
else column[i].right = &column[i + 1];
}
vector<node*> nodes;
for (int i = 0; i < matrix.size(); ++i) {
node* last = nullptr;
for (int j = 0; j < n; ++j) if (matrix[i][j]) {
node* now = new node;
now->row = i;
now->column = &column[j];
now->up = column[j].up;
now->down = &column[j];
if (last) {
now->left = last;
now->right = last->right;
last->right->left = now;
last->right = now;
}
else {
now->left = now;
now->right = now;
}
column[j].up->down = now;
column[j].up = now;
column[j].size++;
last = now;
nodes.push_back(now);
}
}
vector<int> solution;
dlx_search(&head, 0, solution);
for (node* ptr: nodes) delete ptr;
return solution;
}
Exact cover
위에서 Exact cover이란 무엇인지 살펴보았습니다. 언뜻 보기에는 굉장히 한정된 상황에서만 사용될 것으로 보이지만, 적절한 변환을 통해 exact cover 문제로 변환할 수 있는 경우가 굉장히 많습니다.
pentomino
가장 대표적인 예시인 pentomoni부터 생각해보겠습니다. pentomino는 정사각형 5개로 이루어진 polyomino로, 각 정사각형이 최소 1개의 변을 공유해야 합니다.
Pentomino는 총 12가지 종류가 있습니다.

이 12가지 pentomino를 각각 한 번씩 사용하여 6 * 10의 보드판을 덮을 수 있는 경우의 수는 몇 가지일까요? 다음은 그 예시 중 한 가지 경우를 나타낸 그림입니다.
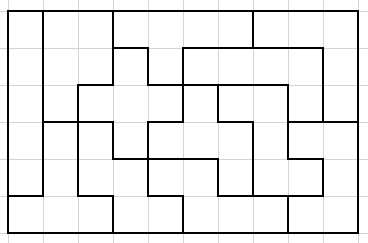
이 문제의 경우 exact cover문제로의 변환을 통해 dlx 알고리즘을 사용할 수 있습니다.
column으로 무엇을 두어야 할지부터 생각해봅시다.
각 pentomino는 1번만 사용되어야 하니, 어떤 pentomino가 사용되었는지를 표시하는 12개의 column을 만듭니다.
그리고 각각의 칸에도 하나의 pentomino만 사용되어야 하니, 각 칸마다 하나의 column을 만듭니다.
이렇게 총 72개의 column이 완성되었습니다.

이제 각 조각별로 놓을 수 있는 모든 경우마다, row를 만들어주면 됩니다. 가령 1번 조각이 다음과 같이 놓여있을 때는 다음 column에 1을 써주면 됩니다.


이제 이 matrix의 exact cover를 찾으면, 이는 12가지 pentomino를 각각 한 번씩 사용하여 6 * 10의 보드판을 덮는 경우가 됨을 쉽게 알 수 있습니다.
실행 시간의 차이를 한 번 살펴볼까요? 참고로, 12가지 pentomino를 각각 한 번씩 사용하여 6 * 10의 보드판을 덮는 경우의 수는 총 9356가지입니다.
평범하게 구현된 brute-force 알고리즘으로 9356가지를 찾는 데에는 46.57초가 소요되었습니다. 하지만, dlx를 이용하면 6.39초만에 정답을 찾아낼 수 있었습니다. 무려 7.3배 가량 더 빠릅니다.
스도쿠
스도쿠의 경우도 한층 더 까다롭지만, exact cover problem으로의 변환이 가능합니다.
마찬가지로 column에 어떠한 정보가 들어가야 하는지를 생각해봅시다.
먼저, 한 칸에는 하나의 숫자만 들어가야 합니다. 따라서 어떤 칸에 들어가는지를 표시하는 column 81개가 필요합니다.
또, 가로줄, 세로줄, 작은 상자 안에 1~9의 숫자가 한 번씩만 들어가야 합니다. 이를 위한 column 243개가 필요합니다.
row는 각 칸마다 1을 넣는 경우, 2를 넣는 경우, …, 9를 넣는 경우를 모두 만들어줍니다. 이렇게 row는 총 243개가 생겨나게 됩니다.
이를 활용한 스도쿠 풀이는 여기에서 살펴보실 수 있습니다.
Conclusion
Knuth’s algorithm X는 사실 Brute-Force 알고리즘의 일종이기 때문에 특별한 점은 없습니다. 하지만, 동일한 Brute-Force일지라도 훨씬 더 빠르게 동작한다면 이는 큰 의미가 있습니다.
재미있게 읽으셨기를 바랍니다. 감사합니다.