A* 알고리즘
안녕하세요?
오늘은 A* 알고리즘에 대해 설명해보려 합니다.
A* 알고리즘은 주어진 출발지에서, 목적지까지 가는 최단 경로를 찾아내기 위해 고안된 알고리즘입니다. 최단경로를 찾아내기 위해 보편적으로 사용되는 다익스트라 알고리즘과의 차이점이 있다면, A* 알고리즘은 완전한 최단 경로를 찾지 않고 최단 경로의 근사값을 찾아내는 것을 목표로 한다는 점입니다.
가까운 노드부터 순차적으로 모두 방문하며 탐색하는 다익스트라 알고리즘과 달리, A* 알고리즘은 현재 위치가 얼마나 좋은 상태인지를 적당한 휴리스틱 함수를 통해 추정하여 점수를 매기고, 그 점수를 바탕으로 탐색을 진행합니다. 정확한 정답을 포기한 대신, 탐색 속도는 다익스트라 알고리즘에 비해 훨씬 빠른 편입니다.
A* 알고리즘의 동작 방식
A* 알고리즘은 다음과 같은 방식으로 동작합니다. A* 알고리즘에 대한 sudo-code는 아래와 같습니다.
OPEN: min heap (초기에 시작점을 포함)
CLOSED: set (초기에 비어 있음)
while OPEN.top() != 도착점:
current = OPEN.top().second; OPEN.pop();
CLOSED.insert(current)
for neighbor in adj[current]:
cost = g[current] + cost(current, neighbor)
if neighbor in OPEN and cost < g[neightbor]:
remove neighbor from OPEN
if neighbor in CLOSED and cost < g[neightbor]:
remove neighbor from CLOSED
if neighbor not in OPEN and neighbor not in CLOSED:
g[neighbor] = cost
OPEN.push({f[neighbor], neighbor})
먼저, 각 노드 n은 f(n)이라는 값을 갖습니다.
f(n)는 g(n)와 h(n)의 합인데, g(n)는 출발지에서 현재 노드까지 도달하는 데에 소요된 비용, h(n)은 현재 노드에서 목적지까지 도달하는데 예상되는 비용입니다. h(n)의 경우, 당연히 정확한 비용을 예측할 수 없으므로 휴리스틱이 들어가게 됩니다.
조금 더 정성적인 의미를 살펴보자면, g(n)은 출발지에서 현재까지 실제로 탐색을 진행한 정보에 대한 가중치, 그리고 h(n)은 현재 앞으로 어떠한 경로를 택할지의 계획에 대한 가중치가 담겨있다고 생각할 수 있습니다.
g(n)은 출발지에서 현재 노드까지 도달하는 데에 소요된 비용이므로, 계산하기 매우 쉽습니다. 다익스트라 알고리즘이나 BFS 등에서 사용되는 방식을 그대로 사용하면 됩니다.
하지만 h(n)의 경우는 조금 더 까다롭습니다. 일반적인 그래프에서 h(n)을 추정하기는 쉽고, 각 노드들이 어떠한 추가적인 정보를 가지고 있어야 합니다. 이번에서는 그래프의 각 노드가 2차원의 어떠한 좌표값을 가진다고 가정하고, 예시를 통해 한번 살펴보도록 하겠습니다.
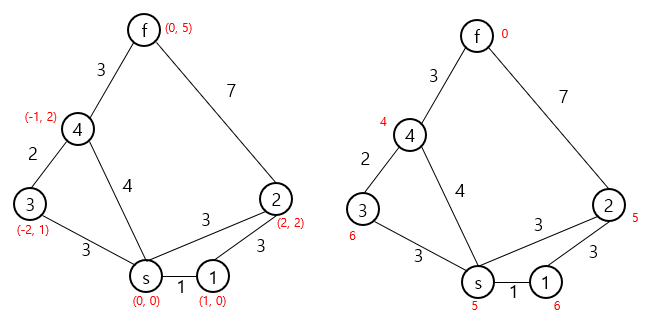
예시의 그래프에서 각 간선들의 비용은 실제 유클리드 거리와 같지 않음에 유의해 주시기 바랍니다.
왼쪽은 노드들이 가지는 좌표값이고, 오른쪽은 해당 좌표값을 통해 계산된 h(n) 값입니다. 여기서는 manhattan distance를 휴리스틱 함수로 사용하였습니다.
OPEN은 앞으로 탐색해야 할 노드들이 담긴 priority queue, CLOSED는 탐색이 완료된 노드들이 담긴 set입니다.
초기에는 OPEN에 시작점만이 포함된 상태로 시작합니다.
이후 OPEN에서 f값이 가장 작은 노드를 꺼낸 뒤, 해당 노드의 이웃들을 탐색합니다.
노드들이 이미 CLOSED나 OPEN에 포함되어 있고 그 g값이 (현재 노드의 g값 + 이동하는 데의 cost)보다 작다면 더 좋은 상태가 있는 것이므로 무시합니다.
그 외의 경우에는 해당 노드를 OPEN에 추가하여준 뒤, g값을 업데이트해줍니다.
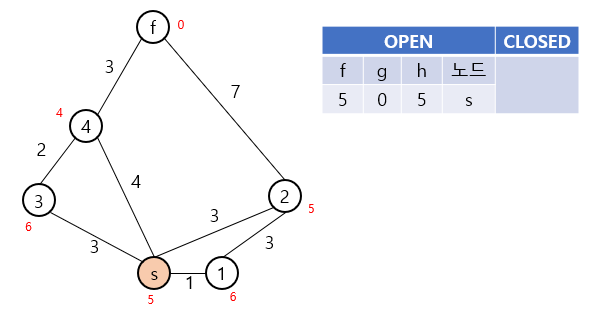
주황색으로 표시된 노드는 현재 탐색이 이루어지는 노드입니다.
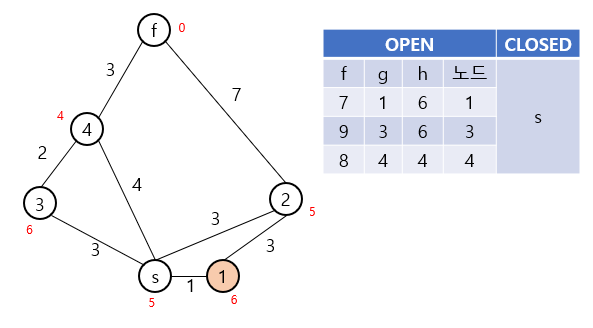
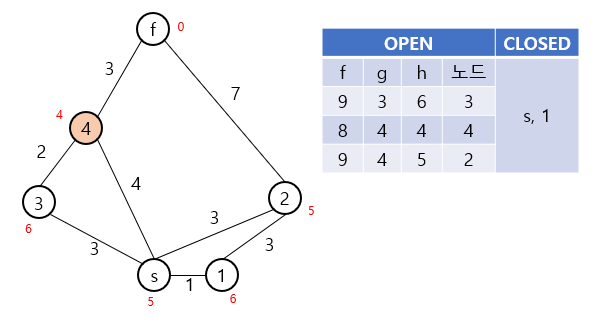
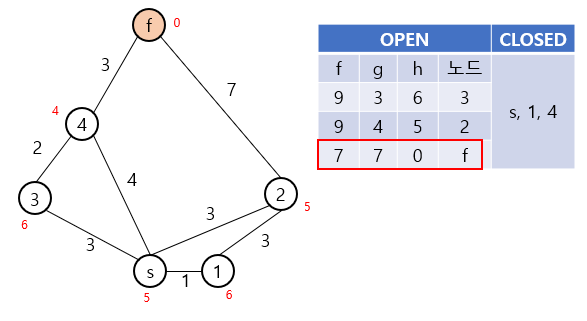
위 예시에서는 s, 1, 4번 노드의 순서대로 탐색이 진행되게 되며, 최종적으로 s-4-f라는 경로를 찾아내게 됩니다.
구현의 특징
A* 알고리즘은 다익스트라 알고리즘과 작동 방식이 굉장히 유사합니다.
다익스트라 알고리즘은 모든 노드 t에 대해 항상 h(t) = 0인 A* 알고리즘의 특수 케이스라고 볼 수 있습니다.
h 함수를 어떻게 잡느냐에 따라 달라질 수 있지만, 일반적으로 노드들의 상태의 점수 추정치인 h(n) 값은 변하지 않으므로, 모든 노드들에 대해 g 값을 저장하는 table 하나와 노드의 f값을 기준으로 하는 min priority queue 하나만 있을 경우 A* 알고리즘을 구현할 수 있습니다.
추가적으로, 다익스트라 알고리즘에서 사용되는 “느긋한 삭제” 등의 코드를 이용하면 더욱 더 간단한 구현을 할 수 있습니다.
아래는 아무런 장애물이 없는 2차원 격자에서, 도착지까지의 경로를 찾는 A* 알고리즘의 구현입니다.
#include <iostream>
#include <queue>
#include <functional>
#define INF 1987654321
using namespace std;
typedef pair<int, int> ii;
typedef pair<int, ii> iii;
int loc[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
ii start = {1, 1};
ii goal = {9, 19};
int h(ii now) {
return 2 * (abs(now.first - goal.first) + abs(now.second - goal.second));
}
int g[10][20];
int main() {
for (int i = 0; i < 10; ++i) for (int j = 0; j < 20; ++j) g[i][j] = INF;
priority_queue<iii, vector<iii>, greater<iii>> pq;
pq.push({h(start), start});
g[start.first][start.second] = 0;
while (!pq.empty()) {
iii poped = pq.top(); pq.pop();
int f = poped.first;
ii now = poped.second;
if (now == goal) break;
int nowg = f - h(now);
if (nowg > g[now.first][now.second]) continue;
nowg++;
for (int k = 0; k < 4; ++k) {
int nextx = now.first + loc[k][0];
int nexty = now.second + loc[k][1];
if (nextx < 0 || nextx >= 10 || nexty < 0 || nexty >= 20) continue;
if (nowg < g[nextx][nexty]) {
g[nextx][nexty] = nowg;
pq.push({nowg + h({nextx, nexty}), {nextx, nexty}});
}
}
}
cout << g[goal.first][goal.second] << '\n';
}
위의 sudo-code에서는 OPEN, CLOSED 등이 있었지만, 하나의 priority queue와 g값을 저장하는 배열만으로 구현 가능합니다.
적절한 h(n)을 선정하는 법
A* 알고리즘에서는 결국, 적절한 h(n) 함수를 설정하는 것이 성능에 가장 큰 영향을 미치는 중요한 문제입니다.
위 예시를 통해 한 번 살펴보겠습니다.
사실 격자에서의 이동은 반대 방향으로만 가지 않으면 최단 경로가 되기 때문에, 최단 경로가 굉장히 많습니다. 하지만 h(n) 함수를 어떻게 설정하느냐에 따라 움직임이 조금씩 달라집니다.
연한 색으로 표시된 부분은, 한 번이라도 접근된 노드(접근된 후 priority queue에 삽입된 적이 있는 노드), 진한 색으로 표시된 부분은 탐색이 이루어진 노드입니다.
Manhattan distance
int h(ii now) {
return 2 * (abs(now.first - goal.first) + abs(now.second - goal.second));
}

Diagonal distance
int h(ii now) {
return 2 * max(abs(now.first - goal.first), abs(now.second - goal.second));
}
x좌표와 y좌표 중 maximum 값을 거리의 척도로 사용한 경우입니다.
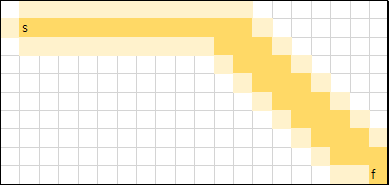
Euclidean distance
int h(ii now) {
int dx = now.first - goal.first;
int dy = now.second - goal.second;
return (int)(2 * sqrt(dx * dx + dy * dy));
}
잘 알려진 유클리드 거리입니다. int 값을 사용하기 위해, int로 casting을 해주었습니다.
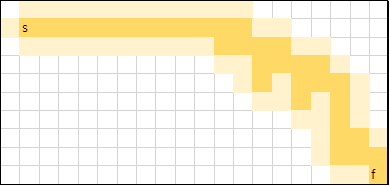
h(n)의 가중치
h(n)에 적절한 상수를 곱해, 크게 만들 경우 h(n) 함수의 영향력이 점점 커지게 됩니다.
예컨대, 아래는 Diagonal distance인데, 왼쪽은 가중치를 2로 준 경우이고 오른쪽은 3으로 준 경우입니다.
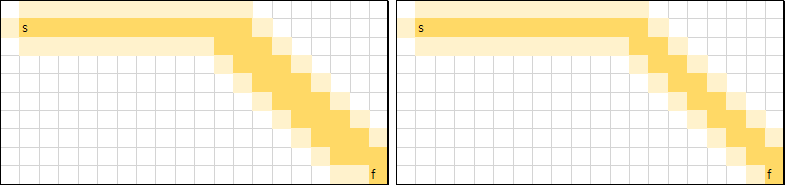
가중치를 크게 줄 수록 조금 더 greedy한 특성이 강해지며, 위와 같은 단순한 경우에는 효율적인 탐색을 진행할 수 있습니다. 하지만 복잡한 경우에는, 잘못된 탐색을 매우 깊게 할 가능성이 생깁니다.
A* 알고리즘을 통한 15-puzzle의 풀이
15-puzzle은 A* 알고리즘을 통해 풀기 매우 적합한 퍼즐 중 하나입니다.
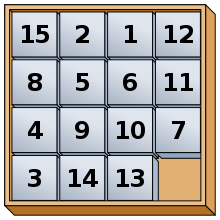
다들 한 번쯤은 해보셨을 듯한 15-puzzle은, 1~15가 쓰여진 타일과 한 칸의 빈칸으로 이루어진 4*4의 퍼즐로 15-puzzle의 목표는 빈 공간을 이용해 타일을 움직여 숫자를 순서대로 배열하는 것입니다.
모든 15-puzzle은 80번의 움직임 안에 풀이가 가능하다는 것이 알려져 있습니다.
parity가 맞지 않는 절반은 움직임을 통해 풀이가 불가능하고, 나머지 절반은 풀이가 가능하기 때문에 퍼즐이 가질 수 있는 전체 경우의 수는 $16! / 2$개로, $10^{13}$ 정도의 숫자입니다. 이는 메모리에 다 들어가지 않는 크기이므로, 다익스트라 알고리즘을 통한 풀이는 불가능합니다.
이 때 A* 알고리즘을 사용하면, 15-puzzle을 효과적으로 풀어낼 수 있습니다.
코드의 구현은 아래와 같습니다. 각 노드의 g값을 효과적으로 저장하기 위해, 노드를 hashing한 값을 key로 하여, map 자료구조를 이용해 parent와 g를 저장하였습니다.
또, h 함수는 1~15까지의 숫자들의, 목표 위치와 현재 위치의 manhattan distance의 제곱의 합을 사용하였습니다.
#include <iostream>
#include <vector>
#include <queue>
#include <map>
#define INF 987654321
using namespace std;
typedef pair<int, long long> il;
struct info {
int f, g, h;
long long p;
int board[4][4];
};
int loc[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
long long HASH(int board[4][4]) {
static int A1 = 1000033, B1 = 1000000007;
static int A2 = 999961, B2 = 999999937;
long long ret1 = 0, ret2 = 0;
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
ret1 *= A1;
ret1 += board[i][j];
ret1 %= B1;
ret2 *= A2;
ret2 += board[i][j];
ret2 %= B2;
}
}
return (ret1 << 32) | ret2;
}
int h(int board[4][4]) {
int ret = 0;
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
if (board[i][j]) {
int t = board[i][j] - 1;
int ii = t / 4;
int jj = t % 4;
int dist = abs(ii - i) + abs(jj - j);
ret += dist * dist;
}
}
}
return ret;
}
/* Goal: To make board
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 0
*/
int main() {
int tc;
cin >> tc;
while (tc--) {
priority_queue<il, vector<il>, greater<il>> open;
map<long long, info> mapping;
info input;
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
cin >> input.board[i][j];
}
}
input.g = 0;
input.h = h(input.board);
input.f = input.g + input.h;
input.p = -1;
long long hvalue = HASH(input.board);
mapping[hvalue] = input;
open.push({input.f, hvalue});
while (!open.empty()) {
il todo = open.top(); open.pop();
int f = todo.first;
info now = mapping[todo.second];
if (now.f < f) continue;
now.g++;
now.p = todo.second;
int x, y;
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
if (now.board[i][j] == 0) {
x = i; y = j;
goto brk;
}
}
}
brk:;
for (int i = 0; i < 4; ++i) {
int xx, yy;
xx = x + loc[i][0];
yy = y + loc[i][1];
if (xx < 0 || xx >= 4 || yy < 0 || yy >= 4) continue;
now.board[x][y] = now.board[xx][yy];
now.board[xx][yy] = 0;
now.h = h(now.board);
now.f = now.g + now.h;
hvalue = HASH(now.board);
if (mapping.find(hvalue) == mapping.end() || mapping[hvalue].f > now.f) {
mapping[hvalue] = now;
open.push({now.f, hvalue});
}
if (now.h == 0) {
vector<long long> ans;
ans.push_back(hvalue);
do {
ans.push_back(now.p);
now = mapping[now.p];
} while (now.p != -1);
// 움직여야 할 block을 순서대로 출력
cout << ans.size() - 1 << '\n';
for (int k = ans.size() - 2; k >= 0; --k) {
long long u = ans[k];
long long v = ans[k + 1];
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
if (mapping[u].board[i][j] != mapping[v].board[i][j]) {
cout << mapping[u].board[i][j] + mapping[v].board[i][j] << ' ';
goto brk2;
}
}
}
brk2:;
}
cout << '\n';
goto clear;
}
now.board[xx][yy] = now.board[x][y];
now.board[x][y] = 0;
}
}
clear:;
}
}
References
아래는 게시글을 작성할 때 참고한 목록입니다.