P VS NP Question

P vs NP Question

들어가며
P NP 란?
여러가지 NP문제들
PSPACE 와 NSPACE
P = NP?
참고

들어가며

예전에 비해 프로그래밍이 좀 더 보편적인 분야로 자리잡으면서, 남녀노소 할 것 없이 많은 사람들이 프로그래밍을 접하고 있다. 또한 문제풀이로 알려진 Problem Solving 쪽을 많은 기업체 또는 학교에서 평가의 기준또는 test로 삼고 있다. 이러한 PS는 여러가지 분야가 있지만, 대부분이 주어진 제한적인 상황안에서 문제를 해결하게 된다. 보통 PS공부를 하기 위해서 알고리즘 공부가 필수라고 얘기한다. 그렇다면 알고리즘이란 무엇일까?

알고리즘을 검색해보면 “문제를 해결하기 위한 일련의 순서적인 계산/풀이 절차/방법” 이라고 설명되어 있다. 매우 직관적이지만 특정한 형식이 서술되어 있지는 않다. 위키백과에서는 알고리즘에 대해 직관을 만족하는 형식적인 정의는 불가능하다고 나와있다.

그렇다면 알고리즘은 실제로 어떻게 이루어진다고 설명할 방법이 없는 것일까? 이를 설명하는 방법은 매우 여러가지 형태가 존재하는데, 그 중에 Turing Machine을 이용한 설명을 예시로 들어보겠다. 튜링 기계는 적당한 규칙과 기호를 이용해 위에서 설명한 알고리즘을 수행해 낼 수 있다.

튜링 기계는 M = { Q, Γ, b, Σ, δ , q0, F } 로 정의 된다. 각 기호들은 아래의 의미를 갖는다.

Q : 상태들의 집합
Γ : 알파벳과 기호들의 집합
b : 테이프가 비어있다는 것을 표시하는 기호
Σ : 입력 가능한 기호들의 집합
q0 : 초기 상태
F : 최종 상태
δ : 전이함수 δ(Q,Γ) -> (Q’,Γ’,{L,R}) 상태와 기호가 주어질 때, 다른 상태로 이동하는 규칙의 집합이다. L,R은 튜링 기계가 테이프에서 일어나는 현상이므로 테이프의 이동을 말한다.

튜링기계와 실제기계는 공간적으로나 시간적으로 차이가 나타난다. 실제기계는 유한한 양의 데이터만을 처리할 수 있기 때문에, 차이점이 존재한다. 세상에 존재하는 모든 알고리즘은 튜링기계로 설명가능하다. 하지만 이는 실제 기계로는 연산의 제한으로 설명을 보장할 수 없다.

이런 알고리즘에 있어서 시간과 공간은 유한하기 때문에 계산적인 문제점은 매우 중요하다. 이 관점으로 문제들을 보았을 때, P NP라는 개념이 등장한다.

P NP 란?

P 와 NP의 정의부터 살펴보자.

P (Polynomial Time) : 다항시간에 문제에 대한 해(Solution)을 찾아낼 수 있는 경우 그 문제를 P클래스에 속한다고 정의한다. 다항시간이라 함은 말그대로 소요 시간에 대한 식이 다항식으로 표현되는 경우를 의미한다.

NP (Non-deterministic Polynomial Time) : NP에 대한 정의는 두가지로 가능하다.

verifier개념 : NP문제라 함은 문제에 대해 제출된 어떤 답(certificate)이 옳은 답(해)인지 아닌지를 판별하는데 다항시간이 걸릴 경우 이를 NP클래스에 속한다고 한다. 가장 유명한 문제로 예를 들어보자. 해밀턴 경로(Hamiltonian path) 는 그래프의 모든 정점을 한 번씩만 지나는 경로를 의미한다. 즉 이 문제의 경우 완전탐색으로 문제의 해를 찾아낼 경우 O(N!) 이라는 시간복잡도 가 나온다. 하지만 해밀턴 경로에 대한 어떤 certificate가 주어졌다고 생각해보자. verifier가 하는 역할은 이 certificate이 유효한 해밀턴 경로인지 확인 하는 것이다. 이것은 다항시간에 가능하다. verifier가 확인해주어야 할 사항들은 1) N개의 노드를 모두 포함하는지 , 2) N개의 노드들이 간선으로 연결되어 있는지 3) 간선에 있어 중복되는 노드가 없는지 이 3가지를 확인주면 된다. 이는 노드와 간선의 다항시간에 해결가능하다. 따라서 해밀턴 경로는 NP클래스인것이다.
decider 개념 : NP에는 P와 조금 달리 Non-deterministic 이라는 말이 붙어있다. 비 결정적이라는 뜻인데, 어떤 language L이 있을 때, 이 L은 decided 되어야 하고, NP클래스에 속하는 알고리즘이라 함은 이 L을 verify하는데 다항시간이 걸리는 것이다. 이게 무슨 뜻이냐 하면, 여기서 튜링머신이 재등장한다. 튜링 기계의 경우 결정론적 튜링 기계(DTM) 과 비 결정론적 튜링기계(NDTM) 으로 나눌 수 있다. 결정론적은 모든 상태들에 대한 전이가 정의되어 있고, 비결정론적 튜링기계는 그렇지 않다. 즉 어떤 input에 대해 Nondeterministic Turing Machine 은 다항시간에 작동하지만 어떨 때는 다항시간에 작동하지 않을 수 있다. 즉 이 NTM으로 어떤 language L이 decidable하면 이 문제는 NP클래스인 것이다.

여러가지 NP문제들

이제 NP클래스에 속하는 NP문제들을 살펴보자.

K-clique problem

clique(클릭) 이란 완전그래프인 부분그래프를 의미한다. 즉 아래의 이미지에서 노드 1,2,3,4 로 이루어진 그래프는 클릭이라고 할 수 있다.

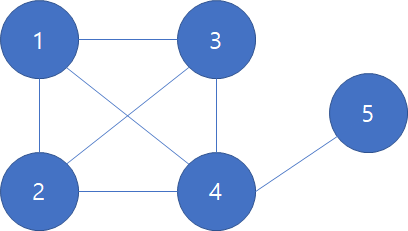
K-clique 문제는 그래프에 존재하는 모든 클릭중 최대 크기를 찾는 것이다. decision class의 k-clique 문제는 NP클래스 이다. 그 이유는 보다시피 verify가 다항시간에 이루어진다.

주어진 부분그래프에대해 완전그래프가 되기 위한 간선들이 모두 존재하는지만 확인해주면 clique임을 증명해줄 수 있다.
Partition problem

분할 문제는 정수로 이루어진 유한집합 S를 두개의 부분집합 A,B (A∩B = Φ) 로 나눌 때, A의 각 원소합과 B의 각 원소합이 같게 만드는 A,B를 찾는 문제이다. 가능한 부분집합의 수는 2^n으로 다항시간안에 해결이 불가능하다. 하지만 verify의 경우 주어진 두개의 부분집합에 대해서 원소합 비교를 하는 O(n) 안에 해결이 가능하므로 NP 문제이다.
Satisfiability problem

충족 가능성 문제는 Boolean Variable(부울 변수)들이 논리합으로 연결된 리터럴 즉 절에 대해 그 절을 참으로 만드는 변수값을 찾는 문제이다. 이 역시 가능한 경우의 수가 2^n으로 다항시간안에 해결이 불가능하지만 verify의 경우 o(n)으로 가능하다. SAT 문제라고도 하며 앞에 숫자를 붙여 2-SAT, 3-SAT 과 같은 형태로 표기하기도 하는데 이는 하나의 절이 포함하는 변수의 최대 수를 말한다. 2-SAT의 경우 다항시간안에 해결이 가능하지만, 3-SAT 이상의 경우 다항시간안에 해결이 불가능하다.

또한 특이하게도 3-SAT 이상의 모든 SAT 문제는 3-SAT 문제로 치환 가능하다. SAT문제를 좀 더 일반화한 문제는 TQBF 문제인데 이는 SAT 문제에서 부울 변수별로 전칭기호가 추가적으로 사용된다. 전칭기호란 all 또는 some of 를 의미한다.
Independent Set

독립 집합은 주어진 그래프에서, 서로 연결하는 간선이 존재하지 않는 정점들의 집합이다. 이 역시 최대크기를 구하는 문제이며, decision type의 문제가 NP class에 속한다. verify의 경우 주어진 정점의 부분집합에 대해 연결하는 간선이 존재하지 않는지를 확인해 주면된다.
Vertex cover

정점 커버 문제는 주어진 그래프에서 정점들의 부분집합을 구하는 문제인데 모든 간선들은 이 정점의 부분집합중 최소 하나의 정점에는 연결되어 있어야 한다. 가능한 정점 커버의 경우의 수 중에서 최소크기의 정점 커버를 찾는 문제이다. verify의 경우에 모든 간선에 대해 주어진 부분집합이 연결되어 있는지 확인해 주면 된다.
Graph Coloring

그래프 색칠하기는 주어진 그래프의 정점을 색칠하게 되는데 서로 인접한 (간선으로 연결되어 있는) 정점의 경우에 다른색으로 칠해야하는 규칙이 있다. 이 역시 NP class에 속하며 verify의 경우 주어진 정점에 대해 모두 색이 칠해져 있는지, 모든 간선에 대해 이어진 두 정점의 색이 모두 다른지를 확인해 주면 O(v+e)에 확인 가능하다.
TSP (Traveling Salesmen Problem) : 외판원 순회 문제로 매우 유명한 NP문제중 하나이다. 주어진 무향 완전 가중 그래프에서 시작점에서 출발하여 모든 정점을 중복없이 방문하고 다시 시작점으로 돌아오는 최단 경로를 구하는 문제이다. 최단 경로를 구하는 문제의 경우 verify 역시 가능하지 않지만, 경로이냐를 묻는 decision type의 문제의 경우 verify는 다항시간에 가능하다. 주어진 경로에 포함된 간선이 정점을 중복하지 않는지, 모든 정점을 포함하는지, 출발 정점과 도착 정점이 동일한지를 확인해주면 된다.
Hamiltonian (cycle) Problem(해밀턴 문제) : 해밀턴 경로는 무향 완전 그래프에서 모든 정점을 중복없이 연결하는 경로를 찾는 문제이다. 시작점에 돌아와야 하는 경우 cycle 문제가 된다. 이 역시 TSP문제와 동일하게 certificate을 찾는데는 O(n!)의 시간복잡도가 소요되지만, verify의 경우에는 다항시간에 해결 가능하므로 NP 클래스에 속하는 문제이다.
ILP (Integer Linear Programming) : AX <= B를 만족하는 정수 X를 찾는 문제입니다. 식의 개수가 하나 인 경우 쉬운 문제이지만, 식이 여러개일 수록 정수인 해를 구하는 것이 복잡해진다. X가 정수라는 제약을 없애고 실수로 늘릴경우 오히려 해를 구하기가 쉬워진다.

PSPACE , NSPACE

PSPACE 와 NPSPACE란 무엇인지에 대해 설명해보겠다. 앞서 말한 P, NP는 모두 다항시간에 해결이 가능한지 또는 verify가 가능한지를 기준으로 클래스가 정의됬다. 반면 PSPACE와 NSPACE는 DTM 또는 NDTM (결정론적 튜링머신, 비결정론적 튜링머신)에서 시간의 제약없이 다항공간만을 사용하여 풀 수 있는 문제들의 집합을 의미한다. P 는 NP의 부분집합인 것은 정의를 통해 쉽게 이해할 수 있다. 그렇다면 NP와 PSPACE의 관계는 어떨까?

결론부터 얘기하면, NP는 PSPACE의 부분집합이다. 이를 증명하기 위해, NP에 속하는 크기 n의 문제에 대해 그 문제를 이루는 certificate의 최대크기가 p(n) 이라고 하자. p(n)은 n에 대한 다항식이다. 이 때 문제애 대한 해가 있는지를 판별하기 위해, 우리는, 가능한 모든 2^p(n)개의 certificate을 순차적으로 확인할 수 있다. 각 시행은 다항시간에 실행될 수 있고, 시행 사이 사이에 공간을 초기화해 줄 경우 필요한 공간의 양도 다항식의 공간이 된다. 이는 사비치 정리라고도 불리며, NP가 PSPACE의 부분집합임을 설명하게 된다.

PSPACE 와 NSPACE는 사실상 위의 사비치 정리를 따라서 동일하다. 시간의 제약없이 공간의 개념만을 관점으로 문제를 class로 나눈 PSPACE NSPACE도 유의깊게 볼만하다.

P = NP?

P class 와 NP class에 대해 공부하게 되면 가장 처음이자 마지막으로 항상 묻는 질문이다. P class와 NP class가 동일할 수 있는지 즉, NP 문제가 다항시간에 해결 가능한지를 묻는 것이다. 당연히 안된다가 답처럼 보이지만 놀랍게도 아직 이 명제는 참인지 거짓인지 증명되지 못했다. 즉 P≠NP를 증명하지 못했다. 이에 앞서 NP-hard와 NP-complete 에 대한 개념을 먼저 집고 넘어가 보자.

NP-hard : NP클래스에 속하는 문제 P가 문제 Q로 reducible(환원가능) 하다면 Q 는 np-hard이다. 여기서 말하는 환원 가능에 대해서는 바로 밑에 설명하도록 하겠다. 간단하게 설명하면 Q가 해결 가능하면, Q를 해결하는 알고리즘을 사용해서 문제P를 해결할 수 있다는 것을 의미한다.
NP-complete : 문제 P가 NP-hard이면서 NP클래스에 속할 경우 P는 NP-complete 이다.

Reducible(환원가능)에 대해 짚고 넘어갈 필요가 있다. 간단하게 얘기하면 어떤 문제를 다른 문제로 치환하는 개념이다. transformation이라고도 할 수 있는데, P라는 문제를 Q라는 문제로 Reduction 한 뒤, Q가 다항시간에 해결가능하면, P 또한 다항시간에 해결 가능함을 의미한다. 아래의 그림처럼 표현해 줄 수 있다.

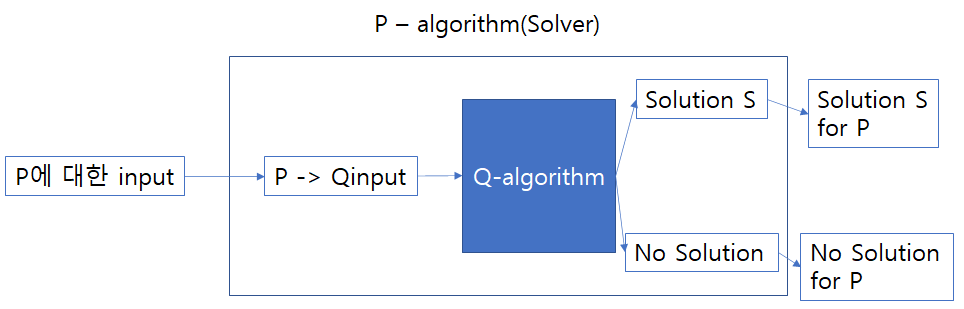
정의 자체는 이해하기 쉽지만 이게 정말 가능한 방법일까? 라는 의문이 드는게 정상이다. 그렇다면 위에서 예를 든 NP클래스의 문제들을 이용해서 실제로 환원가능한 경우들을 알아보자.

Independent Set -> Vertex Cover

그래프 G(V,E)의 독립집합 I(v’,e’)가 있다고 하자. V-I가 바로 G의 Vertex Cover가 된다. Independent Set의 정의에 의해서, v’를 잇는 e’는 존재하지 않는다. 따라서 v에서 v’를 빼게 되더라도, v-v’에 속하는 모든 정점들은 연결되어 있음을 확인할 수 있다.

이로써, Independet Set을 해결할 경우 Vertex Cover도 해결가능한 것이다.
3-SAT -> Indepentdent Set

이는 3-SAT을 그래프 형태로 표현하는 것이다. 3-SAT의 각 절은 3개 이하의 변수로 이루어져 있다. 이 변수들에 해당하는 vertex를 만들고, 논리합으로 연결된 절의 변수들을 edge로 연결해준다. 그리고 x와 not x 는 한쪽이 true면 한쪽은 false여야 하므로 이 또한 간선으로 연결해주는 것으로 표현가능하다. 결국 1과 0이 서로 간선으로 연결되어 선택될 수 없다는 것은 독립집합과 같은 의미를 띄게 됩니다. 따라서 3-SAT을 independent Set으로 reduction한 결과가 됩니다.
SAT -> 3-SAT

앞서 모든 충족가능선 문제는 3-SAT으로 변형 가능하다고 정의했습니다. 먼저 CNF form형식으로 변형한 후에 3-SAT으로 치환하게 되는데 이는 생각보다 매우 간단합니다. 임의의 변수를 추가해 집어넣어주면 됩니다. 기존에 존재하는 변수 A에 (l1,l2) (not l1,l2) (l1,not l2) (not l1, not l2) 를 추가한 총 4개의 절을 만들게 되면 기존 식과 동일하면서 3-SAT으로 표현한 식이 됩니다. 따라서 SAT가 3-SAT으로 치환된 것을 확인할 수 있습니다.
TSP(decision) -> Hamiltionian

해밀토니안 문제와 TSP 간의 차이점은 바로 가중치의 존재와 TSP는 완전그래프라는 것입니다. 즉 해밀토니안의 Solution을 이용해 TSP를 해결하려면 이 차이점을 극복해야합니다. 이는 해밀토니안 문제에서 완전그래프가 되기 위해 없었던 간선들을 추가 한 후에, 추가된 간선에는 가중치 1을 기존에 존재했던 간선에는 가중치 0을 주게 되면, 경로의 가중치합이 0인 TSP solution을 해밀토니안 솔루션으로 찾게 된 것입니다.

위 처럼 많은 종류의 np-complete 문제들이 존재합니다. 이 문제만 해결하면 다른 np문제들이 풀릴텐데! 하는 것이죠.

그렇다면 다시 앞으로 돌아가서 P=NP가 왜 중요한 것일까요? 만약 P=NP가 성립한다면 사실상 거의 모든 문제들이 튜링 기계(실제 세계로는 컴퓨터)로 해결이 가능해진다. 즉 누가 보기에도 P 와 NP는 not equivalent 일 것 같지만 아직 그 해답은 찾아내지 못했다. 항상 P NP에 대한 글이나 책을 보면 마지막에는 이런 말이 적혀있다. P ≠ NP를 증명해보라고

참고

도서 The Golden Ticket: P, NP, and the Search for the Impossible

https://www.amazon.com/Golden-Ticket-NP-Search-Impossible/dp/0691156492