koosaga's profile image

koosaga

November 22, 2020 00:00

2020 ICPC Seoul Regional

algorithm , icpc , competitive-programming

image-20201116223017451

Result Analysis

이번 서울 리저널에서의 각 대학 별 상위 팀은 다음과 같다.

  • 서울대학교: Let Us Win ICPC WF (World Finals 진출 확정)
  • KAIST: Everybody (World Finals 진출 매우 유력)
  • 고려대학교: 1_Hoeaeng_2_Hawawang (World Finals 진출 예상)
  • 숭실대학교: 181920 (World Finals 진출 가능성 있음)
  • 성균관대학교: we need sleep

올해 서울 리저널은 관전자 입장에서 재밌게 볼 만한 요소가 아주 많은 대회였다. 그래서 관전 포인트도 좀 긴 편이다. 온사이트였으면 재밌었을 것 같은데 참 아쉽다.

  • 서울대학교 내전. 올해 서울대학교는 예년처럼 절대적인 최강팀들이 있어서 그 팀이 나가는 게 확실시되는 (혹은 모두의 예상을 깨고 그 예상이 깨지는) 구도가 아니라, 월드 파이널을 누가 나가더라도 이상하지 않은 강팀 여럿이 싸우는 구도로 대회가 진행되었다. 최상위권 참가자들이 한 팀에 뭉치기 보다는 다양한 팀으로 나뉘었기 때문이다. 이런 점 때문에 스코어보드 상에서 (서울대 꼴지 팀) » (그 외 대학 1등 팀) 과 같은 모습이 심심치 않게 보이는, 대규모 스케일의 살벌한 경쟁을 볼 수 있었다.
  • 카이스트 내전. 카이스트는 2021년 이후 월드 파이널 진출이 많이 힘들어질 것으로 예상되기 때문에 올해의 의미가 크다.
  • 월파는 누가? 카이스트에서 아무리 내전을 해 봐야 월파 티켓이 안 떨어지면 의미가 없다. 특히 외침이 없어진 관계로 이번 대회가 유일한 기회이고, 티켓 수도 예측이 잘 안되는 상황의 특수성도 존재한다.
    • 고려대의 1_Hoeaeng_2_Hawawang은 서태수 (cheetose) 김준겸 (ryute) 노세윤 (knon0501) 이 참가한 팀으로 커뮤니티 네임드들이 많다. 이 중 cheetose님은 이미 국제대회 경력이 있다. osu mania 인예 성적은 나빴지만 이와 별개로 많은 사람들이 유력한 월파 후보로 예상하고 있었다.
    • 숭실대의 181920은 카이스트 고려대에도 없는 CF 2레드 팀이다. Ptz Camp를 그냥 씹어먹는 등의 기행으로 여러 사람들에게 충격과 공포를 안겨준 안용현 (FlowerOfSorrow), 코포 레드 코더 이성서 (edenooo), 레드에 거의 근접한 BOJ 랭커 오주원 (JooDdae) 로 구성되어 있다. 필자가 서울대 제외 최강팀으로 예측했으며, 실제로 예선에서는 비서울대 팀중 가장 높은 성적을 받았다. 이 두 팀은 카이스트 상위 3팀과 엮여서 서울대와 비슷한 지독한 난타전을 벌일 것이 예상되었다.

대회 초반 상위 3팀인 1211789, Let Us Win ICPC WF, Ternion은 한 자리 수 단위의 페널티 차이로 팽팽한 줄다리기를 하고 있었으며, 페널티가 큰 다른 팀들은 후방에서 도전을 노리고 있었다. 초반 100분 정도까지 이러한 팽팽한 줄다리기가 계속되었으나, 전반적인 우세는 1211789가 계속 잡고 있는 상태였다. 이 때 Let Us Win ICPC WF가 L과 I를 순서대로 풀면서 1211789를 2문제 차이로 따돌리고, 줄다리기의 주도권을 빼앗는다. 다른 팀들의 추격이 계속되었지만, 최종적으로 Let Us Win ICPC WF가 K를 First solve하게 되면서 줄다리기의 균형이 깨지게 되고, 스코어보드가 Freeze되었다. One Coin이 중반부 2등을 하며 선전하고, 1211789가 모든 문제를 푸는 등의 도전이 있었지만, 240분에 모든 문제를 해결한 Let Us Win ICPC WF 팀에서 주도권을 뺏기에는 역부족이었다. Let Us Win ICPC WF 팀, 축하합니다!

서울대 외 팀들은 전반적으로 Everybody와 1_Hoeaeng_2_Hawawang이 말림 없이 꾸준히 선전하는 모습을 보였다. 초반에는 엎치락뒤치락 하는 모습이 보였으나, 안정화가 되면서 Everybody가 주도하고 그 뒤를 1_Hoeaeng_2_Hawawang이 따라가는 구도가 유지되었다. 결국 프리즈 후 Everybody는 K를 풀면서 World Finals 진출에 쐐기를 박게 된다. 축하합니다!

Problem Analysis

올해 문제는 예년 비해서 약간 쉬운 편에 속한다. PS 커뮤니티에서 연습이 많이 된 standard한 유형의 문제들이 많은데, 주최 측에서는 이 사실을 인지하지 못해서 난이도가 생각보다 쉽게 형성된 것이 아닐까 예상해 본다.

아직 입풀이라서 검증된건 없고 데이터가 곧 공개될 것이니 최선을 다해서 검증해 보겠다…

A. Autonomous Vehicle

기본적으로는 단순한 시뮬레이션 문제에 들어가지만, $n, t$ 가 모두 큰 편에 속해서 효율적인 시뮬레이션을 요구하는 구현 문제이다.

가장 단순한 시뮬레이션 방법은, 현재 기계의 위치와 바라보는 방향을 $(x, y, direction)$ 의 형태로 저장한 후, 문제에서 주어진 규칙대로 다음 위치를 계산하여 한 칸씩 움직이는 것을 $t$ 번 반복하는 것이다. 이렇게 단순히 시뮬레이션을 하면 $O(nt)$ 언저리의 시간 복잡도가 소모되니 시간 초과가 나게 된다. 크게 세 가지 아이디어를 조합하면 이를 $O(n^2)$ 정도의 알고리즘으로 개선할 수 있다.

  • 입력으로 주어진 점 중 교차점이거나 선분의 끝점인 점은 $O(n^2)$ 개이다. 그 외의 점은 선분의 중간에 있으니 한 칸씩 일일이 움직여 줄 필요가 없고 바로 점프해서 건너뛰면 된다. 이렇게 하면 로봇이 있을 수 있는 서로 다른 위치는 $O(n^2)$ 로 줄어들지만 시간 복잡도는 여전하다. 한번 방문한 점을 두 번 이상 방문하게 되기 때문이다.
  • 그런데, 한번 방문한 상태를 다시 방문하게 된다면 사이클에 빠지게 된다. 고로 각 상태마다 “해당 상태에 처음 도달한 시점” 을 기록해 두고, 만약 한번 방문한 상태를 다시 방문하게 된다면, 남은 시간을 사이클의 길이로 나머지를 취한 후 계속 전진하면 된다. 이렇게 되면 다음번에는 다시 사이클에 도달하지 않으니 $O(n^2)$ 개의 상태만 도달한다.
  • 어떠한 상태에서 “다음 상태” 를 찾는 것도 중요하다. 단순히 하면 각 연산 당 대충 $O(n)$ 에서 $O(n \log n)$ 시간 정도가 소모될 것이다. 개선이 필요한 지는 잘 모르겠지만… 하여튼 이를 개선하기 위해서는, 모든 선분에 대해서 해당 선분과 연관된 “중요한 점” (끝점, 그리고 교점) 을 구한 후, 이 “중요한 점” 들의 인접한 쌍 간에 간선을 잇듯이 “다음 위치” 를 지정해 주면 된다. 이 과정은 $O(n^2 \log n)$ 에서 $O(n^2)$ 시간 사이에 구현이 가능하며, 전체 문제도 그 쯤 되는 복잡도에 해결된다. (혹시 $\log n$ 을 어떻게 떼는지가 궁금하다면, 각 교점을 그때그때 정렬할 필요가 없이 전체 선분을 정렬된 순서대로 갖고 있으면 된다는 사실을 관찰하자.)

B. Commemorative Dice

모든 $6 \times 6$ 의 경우 중 첫번째 리스트에서 고른 수가 두번째 리스트에서 고른 수보다 큰 경우의 개수를 세어주면 쉽게 해결할 수 있다. 기약 분수로 출력해야 하는데, 본선 대회니까 gcd는 모두 계산할 수 있을 것이라 믿는다 :)

C. Dessert Cafe

good place가 아니라 bad place 를 센다고 생각하면 좋다. 어떠한 정점 $p$ 가 good place 이기 위해서는

  • 모든 정점 $q \neq p$ 에 대해서
  • 어떠한 아파트 $r$ 이 존재해서 $dist(p, r) < dist(q, r)$

이어야 하니, 반대로 $p$ 가 bad place 이려면

  • 어떤 정점 $q \neq p$ 가 존재해서
  • 모든 아파트 $r$ 에 대해서 $dist(p, r) \geq dist(q, r)$

고로, 모든 아파트와의 거리를 줄이는 다른 정점이 있으면 $p$ 는 bad place 이다. 일단 여기서 확실하게 알 수 있는 것은, $p$ 에 아파트가 있으면 $p$ 는 bad place일 수 없다는 것이다.

$p$ 를 루트로 두고 생각해 보자. 만약 2개 이상의 자식에 대해서 해당 자식의 서브트리에 아파트가 존재한다면, 어느 서브트리로 움직여도 거리가 늘어나는 아파트가 존재하기 때문에 $p$ 는 무조건 good place이다. 만약 정확히 하나에 대해서만 해당된다면, $q$ 를 그냥 그 자식으로 두면 되기 때문에 $p$ 가 bad place가 된다. 고로, 모든 정점이 한 쪽 서브트리에 몰려있다면 $p$는 bad place이다.

이제 bad place의 개수는 정말 여러 가지 방법으로 셀 수 있고, 심지어 쿼리로 들어와도 셀 수 있다. 한 가지 방법은, 각 서브트리 안에 들어 있는 아파트의 개수를 전처리한 후, 현재 노드의 서브트리에 0개의 아파트가 있거나 (모든 아파트가 부모 쪽으로 쏠림) 아니면 자식 중 $k$ 개의 아파트가 서브트리에 있는 자식이 존재하는지를 세는 것이다. 전처리에 $O(n)$ 의 시간이 걸리니, 이 방법을 사용하면 $O(n)$ 에 문제를 해결할 수 있다.

D. Electric Vehicle

먼저 첫 번째 해야 할 관찰은 모든 점에서 1 이상의 배터리를 충전한다고 가정할 수 있다는 것이다. 만약에 어떠한 점을 거쳐가는 데 배터리를 전혀 충전하지 않았다고 가정하자. 두 점간의 거리가 그래프의 가중치 같은 것이 아니라 맨하탄 거리로 정의되기 때문에, 그냥 이 점을 거쳐가지 않고 원래 목적지로 직진하면 경유지의 수를 줄이고 비용도 절약할 수 있다 (삼각 부등식).

이제 이 문제는 DP를 사용하여 나름대로 간단하게 해결할 수 있다. $dp(d, v, w)$ 를 $d$ 개 이하의 점을 방문하면서 시작점에서 $v$ 에 도달하고, 이 때의 배터리양이 $w$ 일 때의 최소 비용이라고 정의하자. 할 수 있는 작업은:

  • 배터리를 충전한다: 상태를 $(d, v, w + 1)$ 로 이동하면 된다.
  • 다른 정점으로 간다: 상태를 $(d + 1, x, w - dist(v, x))$ 로 이동하면 된다.

고로, $(d, w)$ 가 증가하는 순서대로 DP 배열을 채워 나가면 $O(\Delta n w)$ 시간에 문제를 해결할 수 있으나, 느리다.

이제 첫번째 관찰을 사용해서 두 번째 중요한 관찰을 할 수 있다. 어떠한 점 $x$ 에서 다른 점 $y$ 로 이동할 때, 최적해에서는 항상 $x$ 에서의 전기량이 $W$ 이거나 $y$ 에서의 전기량이 $0$ 이다.

증명은 다음과 같다. $x$ 에서의 전기량이 $W$ 미만이며, $y$ 에서의 전기량이 $0$ 초과인 경우가 있는 반례를 생각해 보자. 이러한 반례가 여러 개 있다면, 그 중에서 경유지의 수를 최소화하는 반례를 찾자. 반례에서 처음으로 두번째 관찰이 어긋나는 지점을 생각해 보자. 두 가지 케이스가 있다.

  • 다음에 움직이는 곳의 충전료가 싸거나, 다음에 움직이는 곳이 목적지임: $x$ 에서 남는 전기량이 존재하게끔 충전을 할 필요가 없다. 고로 $x$ 에서 충전량을 줄이면 최적해가 아니게 된다.
  • 다음에 움직이는 곳의 충전료가 비싸거나 같음: 첫번째 관찰에 의해서, 다음에 움직이는 곳에서 0 초과의 전기량을 충전하게 될 것이다. 전기량이 $W$ 가 되거나, 다음에 움직이는 곳에서 충전을 안 해도 될 정도까지 충전을 미리 해 두자. 이렇게 되면 가정에 모순이 되거나, 아니면 경유지의 수를 더 줄일 수 있어서 모순이 된다.

이는, 어떠한 점 $v$ 에서 고려할 필요가 있는 전기량의 경우의 수가 $W - dist(i, v)$ 혹은 $dist(i, v)$ 형태 뿐이고, 개수가 $O(n)$ 이라는 뜻이다. 모든 점에 대해서 가능한 $n^2$ 개의 전기량 구조체를 모두 정렬한 후, 위에서 했던 것과 동일한 방법으로 $(d, w)$ 증가순으로 DP를 채워 나가자. 달라지는 것은, 고려할 필요가 없는 전기량에 대해서 상태를 만들어 주지 않고, 배터리를 충전할 때 $w + 1$ 이 아니라 다음 중요한 전기량으로 바로 점프한다는 것이다. 이렇게 구현해 주면 복잡도가 $O(n^2 \log n + \Delta n^2)$ 가 되어서 시간 안에 문제를 해결할 수 있다.

E. Imprecise Computer

각 round를 방향 그래프로 해석할 수 있다. 정확히는, 모든 $N$ 개의 서로 정점 쌍 간에 정확히 한 방향으로만 간선이 있는 토너먼트 그래프 (tournament graph) 가 된다. 이렇게 볼 경우 $r_i(k)$ 는 $k$ 번 정점의 indegree 이다. 입력으로 주어지는 수열은 $d_k = r_1(k) - r_2(k)$ 라는 수열인데, $i + 1 < j$일 경우 두 그래프 모두 $i \rightarrow j$ 방향으로 간선이 있을 것이기 때문에, 그러한 간선들은 $d_k$ 에 아무 영향도 주지 않아서 무시해 줄 수 있다.

이렇게 되면 문제가 다음과 같이 단순화된다. $N$ 개의 정점을 가지며, $i - (i + 1)$ 간에 방향성 간선이 하나 있는 그래프를 생각할 때, $d_k = r_1(k) - r_2(k)$ 를 만족시키도록 그러한 그래프 2개를 만들 수 있는가가 문제이다.

이는 간단한 DP로 해결할 수 있다. $DP[i][j][k]$ 를, $1 - 2 - \ldots - i$ 번까지 direct를 모두 완료했으며, 첫 번째 그래프에서 $(i-1) - i$ 번 간선의 방향이 $j$이고, 두 번째 그래프에서 $(i - 1) - i$ 번 간선의 방향이 $k$ 일 때, 답이 존재하면 true, 아니면 false라고 하자. $DP[2][][]$ 는 직접 채운 후, $DP[i][][]$ 를 통해서 $DP[i+1][][]$ 를 채워줄 수 있다. 다음에 오는 간선의 방향을 전부 시도해 보고 입력 수열과 맞을 때 dp 값을 전파시켜주면 되기 때문이다. 이러한 방식으로 $O(N)$ 에 문제가 해결된다.

사실, $i \rightarrow (i + 1)$ 로 들어오는 간선의 개수를 고정하면 $(i + 1) \rightarrow (i + 2)$ 로 나가는 간선의 개수도 계산할 수 있어서, 이렇게 식을 써서 계산해 주면 훨씬 간단하게 구현할 수 있다. 이 방법도 $O(N)$ 인데, 내가 이렇게 푼 것이 아니니 관심이 있으면 알아서 생각해 보자.

F. Ink Mix

문제에서 중요한 내용만 정리하면 대략 이렇다.

  • 잉크가 도달하지 않는 병은 무시해도 된다.
  • 어떠한 병에 두 개 이상의 서로 다른 색이 도달하게 된다면 이 병은 mixer이다. mixer는 아예 새로운 색을 assign 받는다.
  • 어떠한 병에 한 개의 색이 도달하게 된다면, 이 병은 그 색을 이어받게 된다.

고로, 예를 들어서 어떠한 정점에 도달 가능한 잉크 색 집합이 같다고 해서 두 정점의 색이 같아지는 것은 아니다. 훨씬 더 강한 조건이 필요하며, 이 조건은 잉크를 받아 온 경로에 관련이 있을 것 같다.

0번 노드라는 더미 노드를 만들어서, 1번 정점부터 $m$ 번 정점까지로 나가는 경로가 있게끔 하자. 0번 정점에서 어떠한 정점 $v$ 로 가는 데 있어서 꼭 거쳐야 하는 노드 $u$가 있다면, $u$ 의 색이 $v$ 의 색과 똑같아 짐을 알 수 있다. 만약에 둘의 색이 다르다면 $u$ 에서 $v$ 로 가는 와중에 $u$ 와 다른 색을 받아들인 mixer가 있다는 뜻이다. 이 중 $u$ 에서의 거리가 최소인 mixer를 잡자. 이 정점에는 두 개 이상의 서로 다른 색이 유입되었다. 이 중 하나는 $u$ 에서 도달 가능한 색일 것이다. 또 다른 하나가 $u$ 에서 도달 가능한 색이라면 이 mixer의 거리가 최소라는 가정에 모순이 된다.

같은 논리로, 어떠한 정점 $v$ 로 가는 데 있어서 꼭 거쳐야 하는 노드가 없다면, $v$ 는 mixer임을 보일 수 있다. $v$ 가 mixer가 아니라면, 같은 색을 공급해 준 노드를 계속 추적해 나가면, 이것이 하나의 노드로 수렴하지 않는 이상 무한히 같은 색의 노드를 늘릴 것이기 때문이다.

결론적으로 우리는 0번 노드에서 $v$ 번 노드로 가는 데 꼭 거쳐야 하는 노드가 있는지를 확인해야 한다. 0번 노드를 루트로 한 Dominator tree를 만들면, 결국 이 문제는 $v$ 번 노드가 0번 노드의 직계 조상인지 아닌지를 판별하는 문제와 동치가 되어서, 매우 쉽게 해결 가능하다. 시간 복잡도는 $O((n + m) \alpha (n))$ 정도이다.

G. Mobile Robot

$i$ 번 로봇과 $i + 1$ 번 로봇의 거리가 모두 정확히 $d$ 이며, 모든 로봇의 위치가 서로 다른 배정은 다음과 같은 두 가지 뿐이다:

  • 1번부터 $n$ 번 로봇이 ${x, x + d, x + 2d, x + 3d, \ldots, x + (n-1)d}$ 위치를 차지
  • 1번부터 $n$ 번 로봇이 ${x, x - d, x - 2d, x - 3d, \ldots, x - (n-1)d}$ 위치를 차지

이 중 두 번째 케이스는 입력 수열을 뒤집은 후 한 번 더 풀어주면 똑같이 해결이 되니, 첫 번째 케이스만 해결하면 된다.

우리는 적절한 $x$ 를 잡아서, $max_{i = 1}^{n} a_i - x - (i-1)d$ 를 최소화하고 싶다. $b_i = a_i - (i-1)d$ 라고 정의하자. 이 경우 우리는 적절한 $x$ 를 잡아서 $max_{i = 1}^{n} b_i - x$ 를 최소화하고 싶다.

어떠한 숫자 $x$ 에 대해서, $maxb_i - x$ 를 계산하기 위해서 고려해야 할 것은 $b_i$ 의 최솟값이나 최댓값 뿐이다. $Mx = \max b_i, Mn = \min b_i$ 라고 했을 때, 위 식은 $max(Mx - x, Mn - x)$ 가 된다. 이를 최소화하는 $x$ 는 $\frac{Mx + Mn}{2}$, 이 때 식의 결과는 $\frac{Mx - Mn}{2}$ 이다.

위에서 뒤집은 케이스를 처리하지 않은 경우, printf("%.1f\n", x) 를 사용하는 등의 경우, long long, 등이 틀릴 만한 이유 중 하나인 것 같다.

H. Needle

약간 요상한(?) 지문이 쓰여 있는데, 결국 읽어야 할 내용은

The upper barrier is one unit above the middle barrier, which is one unit above the lower barrier.

needle can pass the border only through three holes, exactly one from each barrier, which are aligned on a line.

` how many possible escape passages`

이 세가지 뿐이다.

이는 결국 세 수열 $a_i, b_i, c_i$ 가 주어질 때, $a_i + c_j = 2 \times b_k$ 를 만족하는 쌍 $(i, j, k)$ 의 개수를 세는 것이다. 일반적인 경우에는 $O(n^2)$ 를 넘기기가 아주 어려워 보이는 형태이다 (3-SUM 문제와 거의 동일하기 때문). 하지만 이 문제에서는 입력으로 주어지는 수의 범위가 $[-30000, 30000]$ 범위에 속해서 상대적으로 쉽게 해결된다.

각 수의 등장 횟수를 배열에 저장할 것이기 때문에, 모든 수에 30000을 더해서 양수로 만들어 주고 시작한다. $count_a[i], count_b[i], count_c[i]$ 를 $i$ 라는 수가 수열 $a, b, c$ 에서 등장하는 횟수라고 하자 (이 수는 0이거나 1이다). $b_k = x$ 라고 고정하면, 우리가 구하는 것은

$\sum_{x = 0}^{60000} count_b[x] \times \sum_{y = 0}^{2x} (count_a[y] \times count_c[2x-y])$

오른쪽 부분은 잘 알려진 Convolution 형태를 띈다. FFT를 사용하면 두 배열 $A, B$ 가 있을 때

$C[i] = \sum_{x = 0}^{i} (A[x] \times B[i - x])$

를 계산할 수 있음이 알려져 있다. 이는 이런 글을 참고하면 좋다. 구사과 블로그에도 대충의 writeup이 있긴 하다.

이제 $conv[x]$ 를 $count_a, count_c$ 의 Convolution이라고 하면, 위 식은 $\sum_{x = 0}^{60000} (count_b[x] \times conv[2x])$ 가 되어, $M = 60000$ 이라 두면 $O(M \log M)$ 에 해결 가능하다.

여담으로 비트셋을 사용해서 $O(\frac{M^2}{64})$ 에도 해결할 수 있다. 이 방법에 대한 설명은 생략한다.

I. Stock Analysis

풀이 1: $O((N^2 + Q) \log^2 N)$

특별히 부분합 자체에 대해서 신경쓰지 말고 그냥 $\frac{N(N+1)}{2}$ 개의 가중치 있는 구간 (가중치는 해당 구간의 부분합) 에 대한 문제라고 생각한다. $Q$ 개의 쿼리가 주어질 때, 우리는 쿼리로 주어진 구간에 완전히 포함되는 구간 중, 가중치가 $U$ 이하인 최대 가중치 구간을 찾고 싶다. 이러한 문제는 Sweeping을 사용해서 해결하는 경우가 많다. 모든 구간과 모든 쿼리를 가중치 순으로 정렬한 후:

  • 구간이 들어왔을 경우 해당 구간을 적절한 자료구조에 추가한다.
  • 쿼리가 들어왔을 경우, 현재 자료 구조 안에 들어있는 구간의 가중치는 모두 쿼리의 인자 $U$ 이하임이 보장된다 (정렬했으니까). 고로 $U$ 이하 조건을 생각하지 않고 최대 가중치 구간을 구한다.

와 같은 스텝으로 문제를 해결하는 것이다. 이 문제에서도 이러한 호흡으로 접근해 보자.

일단 생각할 수 있는 가장 간단한 자료구조는 2차원 배열이다. $A[i][j]$ 를 $[i, j]$ 구간이 자료구조에 있을 경우 해당 구간의 가중치, 아니면 $-\infty$ 라고 정의하자. 이 경우 구간이 추가되었을 경우 $A[i][j] = Sum[i, j]$ 로 설정하고, 쿼리가 들어올 경우 $ S \le i \le j \le E$ 를 만족하는 모든 $A[i][j]$ 의 최댓값을 계산하면 된다. 이 경우 업데이트에 $O(1)$, 쿼리에 $O(N^2)$ 시간이 필요하다.

이를 최적화하기 위해서는 사실 $S \le i, j \le E$ 조건만 필요하다는 것을 관찰하자. 왜냐하면 저 조건을 만족하면서 $i > j$ 일 경우 어차피 해당 배열에는 $-\infty$ 가 적혀 있을 것이기 때문이다. 고로 이 문제는 2차원 배열에서 $(N, 1)$ 원소를 무조건 포함하는 쿼리가 주어질 때 최댓값을 묻는 문제로 생각할 수 있다. 여기서 $x$ 축을 뒤집으면, $N+i-1 \le N-S+1, j \le E$ 가 되어서 $(1, 1)$ 원소를 무조건 포함하는 일종의 Prefix 쿼리가 되고, 고로 2D Fenwick tree를 사용해서 $O(\log^2 N)$ 시간 업데이트 및 쿼리가 가능하다. 모든 2차원 자료 구조가 되지는 않을 것 같으나, 2D Fenwick tree는 $\log^2 N$ 중에서도 매우 빠르기 때문에 시간 제한 안에 넉넉히 통과한다. (풀이 2를 $N^2\log N + Q\log^2N$ 으로 구현한 것 보다 두 배 이상 빨랐다.)

풀이 2: $O((N^2 + Q) \log N)$

비슷한 방식인데 sweeping 순서를 $U$ 가 아닌 $E$ 로 바꾼다. 모든 구간과 모든 쿼리를 오른쪽 끝점 순으로 정렬한 후:

  • 구간이 들어왔을 경우 해당 구간을 적절한 자료구조에 추가한다.
  • 쿼리가 들어왔을 경우, 현재 자료 구조 안에 들어있는 구간의 끝점은 모두 쿼리의 인자 $E$ 이하임이 보장된다 (정렬했으니까). 고로 시작점이 $S$ 보다 큰 구간들 중, 가중치가 $U$ 보다 작거나 같으면서 가장 큰 구간을 찾는다.

Index(key) 를 $U$ 로 하고, Value를 시작점 $S$ 로 하는 Max segment tree를 만든다. 우리는 $U$ 이하에서 value가 $S$보다 큰 가장 오른쪽 원소를 찾고 싶다. 이는 세그먼트 트리를 루트에서 타고 내려가면서, $U$ 이하 조건을 만족하면서 값이 $S$보다 큰 서브트리 방향으로 따라가는 식으로 해결할 수 있다. 정확히는, $[-\infty, U]$ 구간을 표현하는 세그먼트 트리의 $O(\log N$) 개의 노드를 찾은 후, 이 중 가장 오른쪽에 존재하면서 값이 $S$ 이상인 노드를 하나 찾고, 그리고 해당 노드에서 $S$ 이상을 만족하는 쪽으로 계속 오른쪽으로 내려가면 된다. 이는 세그먼트 트리의 루트에서부터 타고 내려가면서, 값이 $S$ 이상인 가장 오른쪽 노드를 찾는 식으로 가능하다. 세그먼트 트리의 구간 최댓값 쿼리를 하듯이 $[-\infty, U]$ 구간을 나누는 $O(\log N)$ 개의 노드를 딴 후, 그 중 가장 오른쪽에 있는 노드에서부터 내려가면 된다. 이렇게 되면 업데이트와 쿼리가 모두 $O(\log N)$ 에 된다. 사실 쿼리의 개수가 작아서, 가장 오른쪽 노드를 이분 탐색으로 찾아도 쿼리당 $O(\log^2 N)$ 이라서 괜찮다. $U$의 범위가 세그먼트 트리의 배열을 잡기에 너무 큰 것이 문제이지만, 이는 처음에 좌표 압축을 해두면 해결 가능하다.

J. Switches

1번 비트에 대해서만 문제를 해결해 보자. 입력으로 들어온 2차원 행렬을 $A_{i, j}$ 라고 하고, $x_i$ 를 $i$ 번 스위치를 켰으면 1, 아니면 0인 값이라고 하자. 즉 우리가 구하고자 하는 미지수가 $x_i$ 이다. 이 때 조건을 방정식 형태로 써 보면:

  • $A_{1, 1} x_1 + A_{2, 1} x_2 + A_{3, 1} x_3 + \ldots + A_{n, 1} x_n = 1$ (mod 2)
  • $A_{1, 2} x_1 + A_{2, 2} x_2 + A_{3, 2} x_3 + \ldots + A_{n, 2} x_n = 0$ (mod 2)
  • $A_{1, 3} x_1 + A_{2, 3} x_2 + A_{3, 3} x_3 + \ldots + A_{n, 3} x_n = 0$ (mod 2)
  • $\ldots$
  • $A_{1, n} x_1 + A_{2, n} x_2 + A_{3, n} x_3 + \ldots + A_{n, n} x_n = 0$ (mod 2)

이러한 문제는 mod 2에서 $N$ 개의 변수가 있는 연립방정식을 푸는 것과 동일하다. 이제부터는 행렬을 사용하여 이 식을 $Ax = b$ 와 같이 표기한다 (사실 $A$ 의 transpose인 $A^T$ 이지만 적당히 무시하자). 이제 하나의 식에 대해서 가우스 소거법을 사용해서 $O(N^3)$ 에 해결할 수 있다. 이를 $N$ 번 반복하면, $O(N^4)$ 풀이를 얻을 수 있다.

여기서, 행렬이 invertible하지 않다면 답이 존재하지 않는다는 것을 관찰하자. 만약 문제에서 나온 대로 답이 존재한다면, 모든 $2^n$ 개의 가능한 $b$ 에 대해서 항상 해가 되는 $x$ 를 조합할 수 있기 때문이다. 이제 가우스 소거법을 사용해서 행렬이 invertible한지를 판별할 수 있고, invertible하다면 $A^{-1}$ 을 $O(N^3)$ 에 구할 수 있다. 그러면 $x = A^{-1}b$ 와 같이 식을 해결할 수 있고, 벡터와 행렬의 곱은 $O(N^2)$ 에 해결되기 때문에, 이를 그냥 모든 $b$ 에 대해서 해결하면 $O(N^3)$ 에 문제가 해결된다. 사실, $b$ 의 형태가 정확히 하나의 원소만 1인 벡터이기 때문에, 그냥 $A^{-1}$ 의 모든 열에 대해서 켜져 있는 행의 번호를 읽고 출력해 주면, 역행렬을 계산한 후 그냥 printf만 하면 된다.

여담으로, binary field이기 때문에 가우스 소거법을 bitset으로 구현하면 짧고 간단하며, 심지어 64배 빠르기까지 하다. 이 경우 복잡도는 $O(\frac{N^3}{64})$ 이다.

K. Tiling Polyomino

이 문제에서 polyomino는 연결되어 있고, 구멍이 없으며, 인접한 다른 셀의 개수가 정확히 1개인 경우가 없는 것이 보장된다. 세 번째 조건이 대단히 중요하고, 아마 이 조건이 없으면 NP-complete일 수도 있을 것 같다. 인접한 다른 셀의 개수가 정확히 1개인 셀을 꽁지 라고 부르자.

가장 쉽게 관찰할 수 있고 관찰해야 하는 사실은, $w \times h$ 직사각형은 $w, h$ 가 모두 1이 아닌 이상 항상 분할할 수 있다는 것이다. 방법도 아주 간단하다. 일반성을 잃지 않고 $w \le h$ 라 하면 $h \geq 2$ 이다. $w$ 개의 줄로 분리한 후 $1\times 2$ 타일을 쭉 늘어놓고, $h$ 가 홀수면 마지막 타일만 $1 \times 3$ 으로 바꿔주면 된다.

전체 문제에서도 이 전략이 거의 먹힌다. 각 가로 줄에 대해서 개별적으로 문제를 해결해 준 후, 연속된 1에 대해서 위 방법으로 대충 채워주면 될 것 같기 때문이다. 물론, 예제에도 나와있듯이 위 방법은 대략 이런 입력에서 잘 작동하지 않는다.

111
111
010
111
111

이 입력을 대충 가로로 분해하고 생각해보면 3번째 행에 $1 \times 1$ 격자가 놓이기 때문이다. 그런데 이런 경우가 아니면 웬만하면 된다. 그러니까 이러한 경우를 잘 처리해 보자.

구멍이 없고 연결되어 있는 polyomino는 일반적으로 Simple Rectilinear Polygon이라고 부른다. Rectilinear polygon은 서로소 직사각형으로 이루어진 트리 형태로 분해해서 관리할 경우 여러 문제들을 쉽게 해결할 수 있음이 알려져 있다 (IOI 2012 Ideal City, BOI 2014 Demarcation). Simple polygon을 삼각분할 한다는 것이 어떤 뜻인지를 생각해 보면, Rectilinear polygon을 직사각형으로 분할하는 것의 이점을 알 수 있을 것이다.

이 문제에서도 주어진 입력을 이렇게 트리로 분할한다. 분할하는 전략은 그냥 단순하게 연속한 가로 구간을 하나의 정점으로 보는 것이다. 이제 트리를 top-down으로 타고 내려가자. 만약에 현재 보는 노드의 길이가 2 이상이면, 쉽게 해결할 수 있다.

문제는 현재 보는 노드의 길이가 1일 때이다. 이 때는 꽁지와 꽁지의 부모와의 관계를 끊고, 해당 입력을 꽁지가 정확히 1개 달려 있는 Rectilinear polygon 으로 해석하자. 여기서부터 전략을 바꿔서, 연속한 가로 구간이 아니라 세로 구간 에 대해서 칠해주는 식으로 전략을 바꾼다. 꽁지는 어차피 아래에 노드 하나가 존재하며, 그 노드랑 세로랑 연결되어야 하니까, 어느 정도 세로로 연결하는 것은 피할 수 없으니 그냥 다 세로로 칠해주는 것이다.

꽁지와 꽁지의 부모를 끊었다고 해서 다각형이 simple rectilinear polygon이 아니게 되는 것은 아니기 때문에, 이 전략은 또 다시 노드의 길이가 1일 때가 생기기 전까지 올바르다. 노드의 길이가 1이 된 경우에는, 또 다시 해당 부분을 꽁지로 자른 후, 전략을 다시 가로 구간 으로 바꿔준다. 이런 식으로 길이 1의 노드를 만날 때마다 전략을 혼합해서 사용하면, 문제를 해결할 수 있다. 구현은… 나는 직접 트리를 딴 후에 열심히 노력했는데, 더 쉬운 구현이 분명히 존재할 것 같으니 직접 생각해보자.

L. Two Buildings

$i \geq j$ 이면 항이 음수가 되기 때문에 굳이 $i, j$의 대소 관계는 고려할 필요가 없음을 감안하자. 이 문제는 $N$ 개의 빨간 점 $(i, h_i)$ 와 $N$ 개의 파란 점 $(j, -h_j)$ 가 주어졌을 때, 파란 점을 오른쪽 아래, 빨간 점을 왼쪽 위로 하는 직사각형의 최대 넓이를 구하는 문제와 동일하다. (만약 위치가 오른쪽 아래 / 왼쪽 위가 아니면 넓이를 음수로 가져가거나 고려하지 않는다). 해당 문제는 World Finals 2017의 기출문제로 유명한 Money For Nothing 과 동일한 문제로, 동일한 풀이를 사용하면 된다. 여기서 설명을 끝내고 싶지만.. 글의 완전성을 위해 해당 문제를 푸는 방법을 소개하도록 하겠다.

다음과 같은 두 가지 성질이 성립한다.

  • 어떠한 빨간 점 $p = (x, y)$ 의 왼쪽 위에 다른 빨간 점 $q = (x^\prime, y^\prime)$ 이 존재한다면 ($x^\prime \le x, y^\prime \ge y$), 이 빨간 점은 최적해에 포함되지 않는다. 최적해가 $p$ 를 포함한다면 $q$ 로 바꿔줘서 넓이를 늘릴 수 있기 때문이다.
  • 어떠한 파란 점 $p = (x, y)$ 의 오른쪽 아래에 다른 파란 점 $q = (x^\prime, y^\prime)$ 이 존재한다면 ($x^\prime \ge x, y^\prime \le y$), 이 파란 점은 최적해에 포함되지 않는다. 최적해가 $p$ 를 포함한다면 $q$ 로 바꿔줘서 넓이를 늘릴 수 있기 때문이다.

이 때, 이러한 최적해에 포함되는 빨간 점과 파란 점은 지금까지 만난 점들의 높이 최소 / 최댓값을 관리하는 식으로 쉽게 $O(N)$ 에 구할 수 있다. 이제 대충 우상향 형태를 띄는 빨간 점 체인과 파란 점 체인을 구할 수 있다. 빨간 점 체인을 $x$ 좌표 증가순으로 $r_1, r_2, \ldots, r_k$, 파란점 체인도 $x$ 좌표 증가순으로 $b_1, b_2, \ldots, b_l$ 이라고 하고, $cost(r_i, b_j)$ 를 $(b_j.x - r_i.x) \times (r_i.y - b_j.y)$ 로 정의하자. 다음과 같은 사실을 보일 수 있다.

  • Theorem. $opt(i)$ 를 $cost(r_i, b_j)$ 를 최대화하는 $j$ (그런 것이 여러개라면 그 중 최소) 라고 정의하자. $opt(i) \le opt(i + 1)$ 이 만족된다.

  • Intuition by picture. $cost(r_i, b_j) > 0$ 이라고 가정할 경우 다음과 같은 그림으로 쉽게 증명할 수 있다. $opt(i) > opt(i + 1)$ 일 경우 둘을 바꿔서 $cost(i, opt(i))$ 합을 증가시킬 수 있고, 가정에 모순이다.

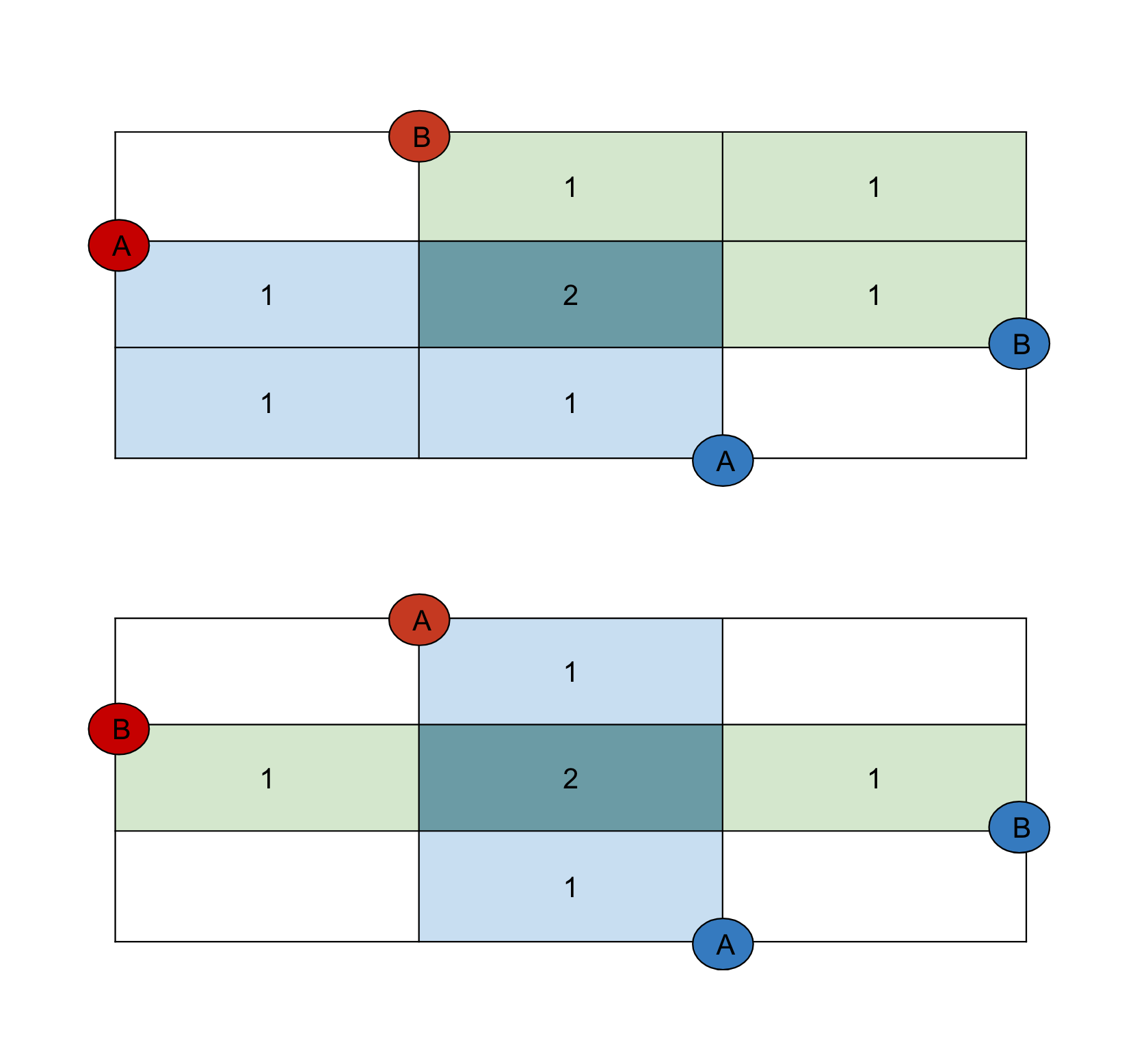
    image

  • Proof. $j = opt(i), k = opt(i + 1)$ 라 하자. $j > k$ 이다. $cost(r_i, b_k) > cost(r_i, b_j)$, $cost(r_{i + 1}, b_k) \le cost(r_{i + 1}, b_j)$ 를 만족한다. 즉, $cost(r_i, b_j) + cost(r_{i + 1}, b_k) < cost(r_i, b_k) + cost(r_{i + 1}, b_j)$ 이다. 식으로 풀어서 쓰면

    $(b_j.x - r_i.x) \times (r_i.y - b_j.y) + (b_k.x - r_{i+1}.x) \times (r_{i+1}.y - b_k.y) < (b_j.x - r_{i+1}.x) \times (r_{i+1}.y - b_j.y) + (b_k.x - r_i.x) \times (r_i.y - b_k.y)$

    헷갈리지만 잘 정리해 보면

    $b_j.x \times (r_i.y - r_{i + 1}.y) + b_k.x \times (r_{i + 1}.y - r_i.y) < r_i.x \times (b_k.y - b_j.y) + r_{i + 1}.x \times (b_j.y - b_k.y)$

    $(b_k.x - b_j.x) \times (r_{i + 1}.y - r_i.y) < (r_i.x - r_{i + 1}.x) \times (b_k.y - b_j.y)$

    그런데 가정에 의해

    $r_i.x < r_{i + 1}.x, b_j.x < b_k.x, r_i.y < r_{i+1}.y, b_j.y < b_k.y$

    이니 좌변은 양수, 우변은 음수이다. 모순.

고로, 이제 $opt(i)$ 는 구사과 블로그에 소개된 동적 계획법을 최적화하는 9가지 방법 글을 참고해서 최적화하면 된다. Divide and Conquer optimization, Monotone queue optimization 이 가능하며, 전자가 구현하기 가장 간단할 것이다. 사실 World Finals의 문제는 $i, j$ 의 대소 관계를 묘하게 고려해야 해서 이 문제보다 약간 더 어려운데, 이 문제에서는 그냥 이 내용을 가지고 D&C opt를 하면 된다.