혹시 기하 문제를 좋아하시나요? Problem Solving에 나오는 어려운 기하 문제는 다양한 예외처리와 기하 문제 특유의 방향성 때문에 인해 일반적으로 기피대상입니다. 우연히 맞닥뜨린 문제인 BOJ 18190번 ‘촛불과 그림자’도 악명 높은 기하 알고리즘 문제로, solved.ac에서 Ruby V로 평가되는 고난이도의 문제입니다. 알고리즘 구상부터 해결까지 대략 일주일 정도 걸린 시련의 길을 반면교사로 삼고자 이렇게 글을 쓰게 되었습니다.
이후엔 촛불과 그림자 문제의 상세한 아이디어와 풀이가 나오므로 유의하시기 바랍니다.
‘촛불과 그림자’란?
두 볼록 다각형 $A$와 $B$가 있습니다. $B$는 $A$ 안에 교점 없이 완전히 포함됩니다. 점으로 표현되는 촛불의 위치가 주어질 때, 이 촛불이 $A$ 외부 또는 경계에 존재하거나 $B$ 내부 또는 경계에 존재하면 그렇다고 판별하고, 둘 다 아니면 이 촛불이 만드는 그림자의 넓이를 계산해야 합니다. 각 촛불은 독립적이며 총 $Q (\leq 10^5)$개 주어집니다. 두 볼록 다각형의 꼭짓점의 개수 $N$, $M$은 최대 $10^5$개이며 좌표는 절댓값이 $10^6$ 이하인 정수입니다.
실제 대회와 Open Contest에서 풀리지 않았고, 검수진을 제외하고 푼 사람이 거의 없는 문제입니다.
해결 일지
나는코더다 2019 송년대회를 이 문제를 제외하고 전부 풀어보아서, 어떻게 풀지 고민하고 있던 차에 해설지를 봤습니다. 4단계에 걸친 풀이가 아주 간략하게 적혀 있었습니다. 실제로 구현해본 적이 없는 기하 함수들이 많아서 구체화가 오래 걸렸습니다. 안타깝게도 디버깅이 훨씬 더 오래 걸렸습니다.
1월 14일: 구상
풀이를 이해하고 구현하기 시작했습니다. 기하가 오랜만이라 쉽지 않았습니다. 코드가 길어지리라 생각해 구조체 안에 함수를 여럿 만들었습니다. 1단계는 make_hull과 contains, 2단계는 tangent, 3단계는 halfline과 intersection, 4단계는 calc가 담당했습니다. 편의상 쿼리로 주어진 점을 $P$라고 하겠습니다.
- 다각형을 입력받고
make_hull로 반껍질을 Andrew’s Monotone Chain Algorithm으로 계산합니다. 외적의 누적 합도 미리 계산해둡니다. - 1단계
contains는 각 껍질별로 선분을 구성하는 두 점과 $P$의 외적값의 부호 판별(ccw)을 바탕으로 이분 탐색을 진행합니다.

- 2단계
tangent는 $B_0$가 접점인지 아닌지 ccw로 판별합니다. 접점이 아닐 경우 $\overleftrightarrow{PB_0}$ 와 $B$의 또다른 접점이 어느 선분($\overline{B_{k}B_{k+1}})$에 있는지 이분 탐색으로 구하며, 접점일 때는 이 과정을 생략할 수 있습니다. 그럼 $\overleftrightarrow{PB_0}$ 기준으로 양쪽에 접점이 한 개 ($B_0$가 접점일 경우 나머지에)씩 존재하기 때문에 이분 탐색을 진행할 수 있습니다. 구한 두 접점을 $Q_0$, $Q_1$이라 하겠습니다.
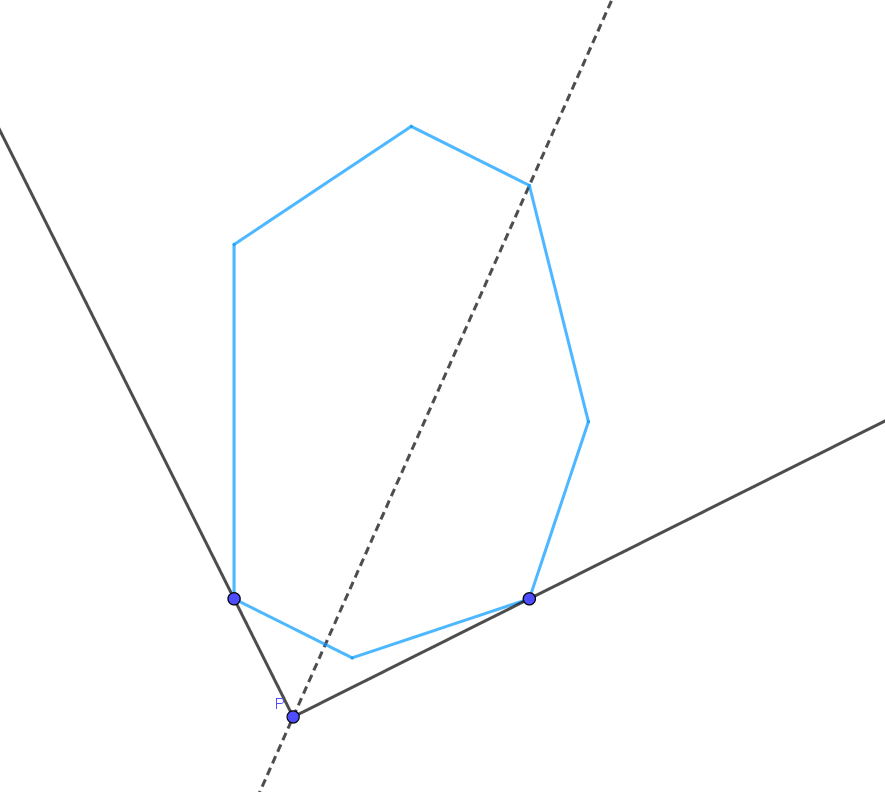
- 3단계
halfline은 $\overline{PA_0}$과 $\overline{PA_k}$ 사이에 $\overrightarrow{PQ_0}$가 있는지between함수를 호출해 이분 탐색으로 확인한 후, $\overrightarrow{PQ_0}$와 $A$의 교점을intersection을 호출해 계산합니다. $Q_1$도 동일한 작업을 합니다.

- 4단계
calc는 계산한 교점 $T_0$, $T_1$과 $Q_0$, $Q_1$의 위치와 인덱스를 종합하여 그림자와 $B$를 포함한 넓이를 계산합니다. 신발끈 공식과 외적의 누적합을 통해 $\mathcal{O}(1)$에 계산할 수 있습니다.

위 그림의 굵은 선분이 $P$로 인해 만들어진 새로운 선분이며, 그림자를 구성하는 나머지 선분은 다각형의 변입니다.
겉으로 보기엔 풀이가 그럴 듯해 보이지만 이 때만 해도 25번이나 고배를 마실 줄은 몰랐습니다.
1월 15일: 첫 제출에서 59%까지
처음에 짰을 때는 예제도 안 나와서 이리저리 코드를 고쳤습니다. 약간 수정하니 하나밖에 없는 예제가 나와 제출해보았습니다. 7588B의 코드는 장렬하게 바로 틀렸습니다를 받았습니다. 조그마한 예제를 만들어보았는데 넓이가 음수가 나오는 걸 보고 놓친 게 많음을 느꼈습니다.
3 3 5
-4 0
4 0
0 4
1 1
0 2
-1 1
0 3
-1 2
1 2
-2 1
2 1
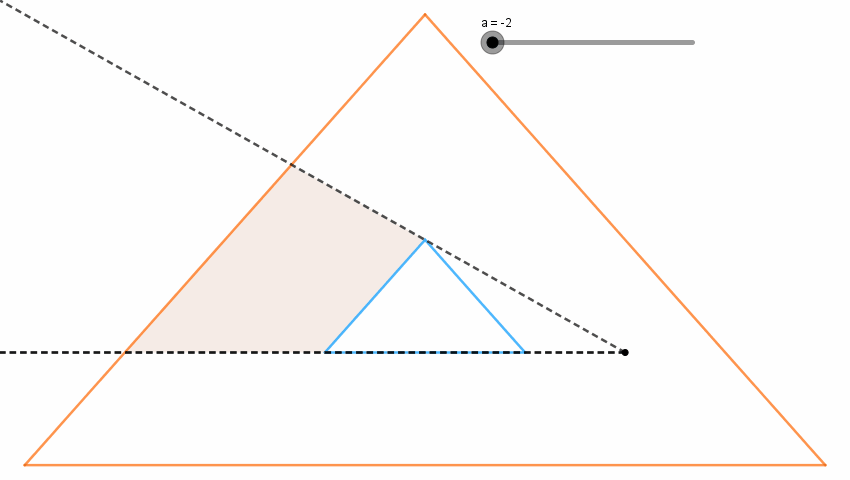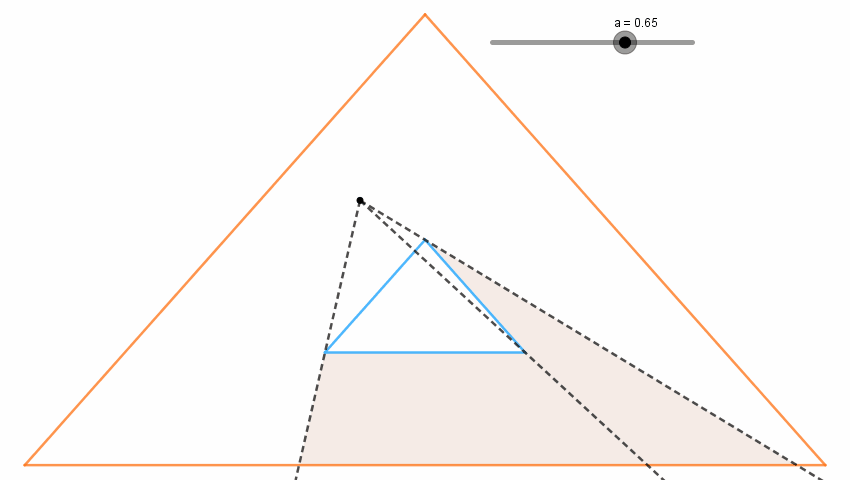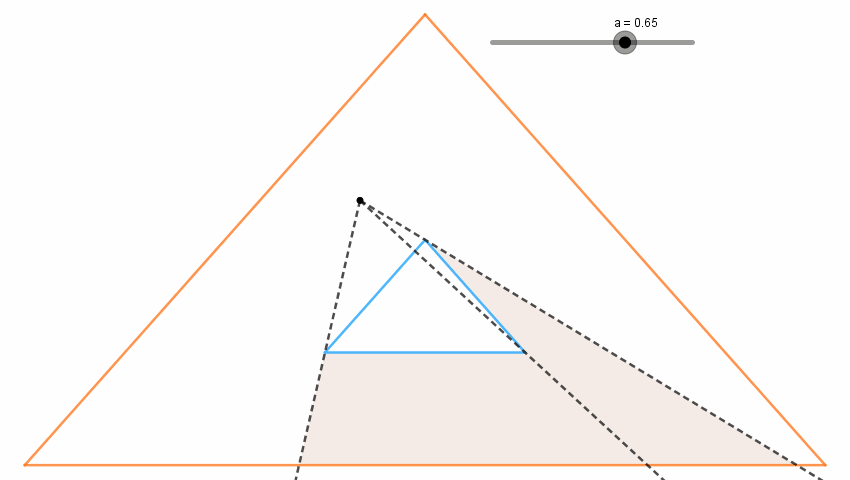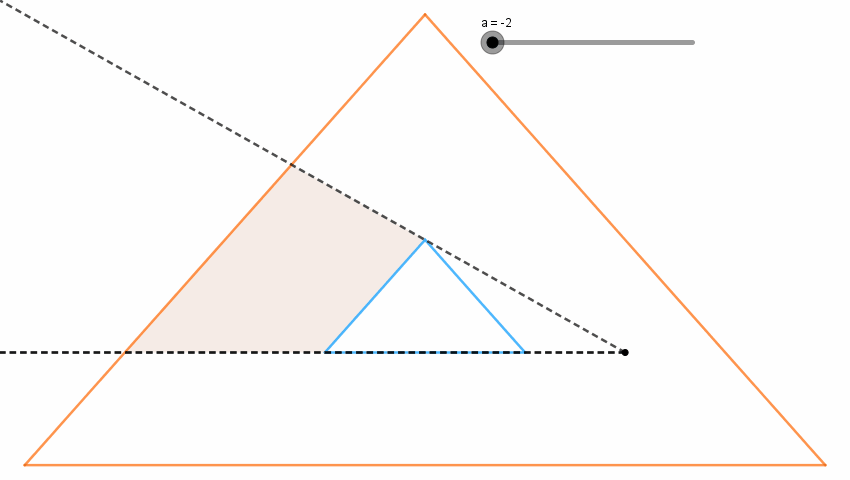
도형과 쿼리가 $y$축 대칭이기 때문에 답이 똑같이 나와야 하는데 한 쪽은 크게 나오고 한 쪽은 음수가 나오고 아수라장이었습니다. 살펴보니 tangent 함수에서 $B_0$가 접점이지만 $B_1$이나 $B_{m-1}$이 접점이 아닐 때 처리가 안 되고 있었습니다. 그리고 넓이 계산에도 오류가 있었습니다. between 함수도 두 벡터의 방향이 동일할 때를 놓치고 있었습니다. 고쳤더니 16%까지 올라갔습니다.
아직까지는 반례가 금방 나왔습니다. 다음 반례도 삼각형 안에 삼각형이 있는 입력입니다.
3 3 1
0 10
-1 -1
10 0
0 1
1 0
1 1
0 0
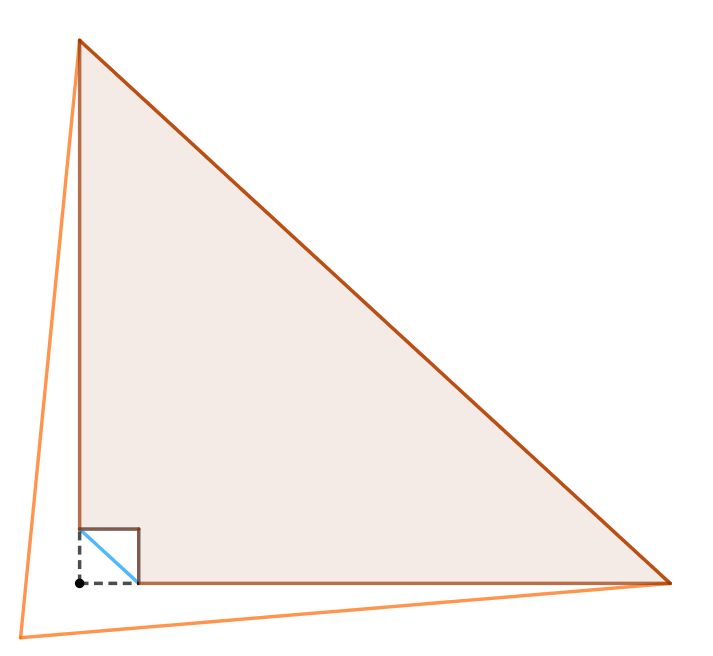
between 함수를 약간 더 고쳤고, 이분탐색도 살짝 수정했습니다. 그러나 contains에 있던 알고리즘의 구멍을 발견하고 허탈했습니다. $P$가 $y$축에 평행한 다각형 선분 위에 있을 때 판별이 잘 안 되었기 때문입니다. 이번엔 정사각형 안에 정사각형이 있는 반례입니다.
4 4 10
-4 -4
4 -4
4 4
-4 4
-1 -1
1 -1
1 1
-1 1
-4 -6
-4 -2
-4 2
-4 6
-1 0
1 0
4 -6
4 -2
4 2
4 6

이를 고치고 선분을 기준으로 점이 위쪽에 있는지 아래쪽에 있는지 계산하는 onSegment함수를 만들었습니다. 제출하니 59%까지 진전이 있었습니다. 이 때까지만 해도 금방 ‘맞았습니다!!’를 받을 줄 알았습니다.
1월 16일: 의심의 시작
contains에 있던 이분 탐색의 자잘한 범위 실수를 고쳤지만 59퍼센트의 벽은 견고했습니다. 때문에 ‘데이터가 틀린 게 아닐까’라는 잘못된 생각에 빠질 때도 있었습니다. assert를 넣기 시작했지만 데이터의 견고함만 깨달았습니다. 저의 도전을 보고 Lawali님이 참전하였는데 하루만에 66%까지 가셨습니다. 그러나 서로 ‘왜 틀릴까요 ㅠㅠ’ 정도의 의견 교류에 그쳤습니다.
1월 17일: 실수 오차?
onSegment를 계속 고쳤으나 성과가 없어서 assert를 걸면서 제출을 계속했습니다. 코드의 잘못된 점은 찾지 못했습니다. 결국 검수자였던 koosaga님께 정답 코드 몇 개를 요청해서 받았습니다. 코딩 스타일이 저랑 달라 이해가 쉽지 않았지만, 몇몇 부분에서 진전이 있었습니다. 대부분 제가 이분 탐색으로 처리한 부분을 lower_bound 함수로 쉽게 정리했고, 넓이를 계산할 때 교점을 구하지 않고 처리했습니다.
저는 교점 $T_0$, $T_1$과 $Q_0$, $Q_1$의 좌표를 전부 고려하여 직접 신발끈 공식을 사용했습니다. $T_0$와 $T_1$의 좌표 계산에 실수 연산이 필요하고, 실수 좌표에 신발끈 공식을 사용하면 실수 오차가 일파만파 퍼질 수 있습니다. 이럴 필요 없이 교점을 직접 계산하지 않고 외적값만 계산할 수 있습니다. $T_0$쪽에서는 $P \times T_0$(또는 $Q_0 \times T_0$)와 $T_0 \times A_k$를 계산해야 하는데, $P \times T_0$는 $P \times Q_0$의 상수배이고 $T_0 \times A_k$도 $A_{k-1 \mod n} \times A_k$의 상수배입니다. 각각의 상수는 외적의 성질을 이용해 계산할 수 있고, 이러면 신발끈 공식에서 좌표끼리 곱하는 과정 없이 외적값을 그대로 넣을 수 있습니다. 실수 연산이 줄기 때문에 실수 오차도 덜합니다. $Q_1$도 똑같이 풀 수 있습니다.
이 때 답이 다르게 나와야 하는데 실수 오차로 같게 나오는 예제를 하나 만들었습니다.
4 4 2
-1000000 -1000000
1000000 -1000000
1000000 1000000
-1000000 1000000
999998 999998
-999998 999998
-999998 -999998
999998 -999998
999999 -999998
999999 -999999
그러나 이 부분을 개선해도 이 예제의 답이 그대로 나와 다른 부분을 점검하기로 했습니다.
다른 함수에 문제점이 있지 않을까 싶어 몇몇 함수를 갈아엎었습니다. make_hull은 Monotone Chain Algorithm 대신 std::rotate로 해결했으며, contains를 재작성해봤습니다.
1월 18일: 휴식
왜 틀렸는지 도저히 모르겠어서 별다른 작업을 하지 않았습니다.
1월 19일: 성공
contains를 재작성했으나, 기존의 contains과 새로 짠 contains와 정답 코드의 contains 역할의 함수가 동일하다는 사실만 깨달았습니다. between 함수의 예외 처리를 하나 추가했지만 그대로였습니다. 설마 calc 함수가 잘못되었나 싶어 assert를 넣었지만 런타임 에러는 나오지 않았습니다.
위의 반례를 정해 코드에 넣어봤는데, 저의 코드만 절대 오차가 1e-6 이상 나타남을 확인했습니다. 첫 번째 쿼리의 답은 7999972000023/999998으로 대략 7999987.99999899999799999599999 정도이며, 두 번째 쿼리의 답은 15999952000032/1999997으로 7999987.99999799999699999549999 정도입니다. 답이 1e-6정도밖에 차이가 나지 않습니다. 그런데 제 프로그램은 둘 다 7999988.0이라고 주장하고 있었습니다. 이전에 썼던 넓이 계산 방식 코드도, 정답 코드를 보고 오차를 개선한 코드도 마찬가지였습니다. 실수 연산 횟수에 차이가 없음에도 이 정도 오차가 발생해서 당황스러웠습니다. long double을 써보았지만 답은 변하지 않았습니다.
정말 포기해야 하나 싶은 순간에 코드 한 줄이 눈에 들어왔습니다.
res += (q1 / p) * 1.0 * a / (b-a)
직접 캐스팅을 하면 오차가 줄지 않을까 싶어
res += (q1 / p) * (long double)a / (b-a)
로 변경하였고 calc의 나머지 실수 연산도 이렇게 바꾸었는데 세상에, 59퍼센트를 넘고 맞았습니다를 받았습니다.

그동안 실수 연산 헛배웠구나 싶었습니다. 오기로 다른 문제에 제출도 안 하고 있었는데 드디어 족쇄에서 풀려났습니다. 위 반례에 저의 정답 코드를 double로 형변환하니 답이 7999988.0이 나와 상당한 실수 정밀도를 요구함을 알 수 있었습니다.
결론
한 문제를 푸는 데 이렇게 오랜 시간과 많은 시도를 해보긴 정말 오랜만입니다. 알고리즘 문제를 오랫동안 풀어왔지만 아직 배울 게 많다는 당연한 사실을 다시금 깨달았습니다. 캐스팅도 잘못 들인 습관 때문에 생각을 안 했었는데 힘겹게 배웠습니다. 기하 문제는 특유의 구조가 신기해서, 앞으로 많이 풀어보고 싶습니다. 다음에 어려운 문제를 풀 때는 git과 연동하고 데이터 탓은 지양해야겠습니다.
풀이를 위한 그림을 어떻게 그릴까 고민이 많았습니다. 태블릿이 가장 편하지만 없어서, 3Blue1Brown이 영상을 만들 때 쓰는 manim을 배워볼까 한 시간 정도 생각해봤습니다. 수많은 Python 디펜던시 오류와 버전 문제를 겪고 GeoGebra로 선회했습니다. 쓰다보면 약간 답답한 구석이 있고 중노동을 요구하지만 이만한 무료 프로그램이 없습니다.
이 포스트를 보고 혹여나 촛불과 그림자를 도전해보시는 모든 분에게 행운을 빕니다.