March 21, 2021 08:00

Disjoint Set

Disjoint Set(서로소 집합, 분리 집합)이란 서로 공통된 원소를 가지고 있지 않은 두 개 이상의 집합을 말합니다. 모든 집합들 사이에 공통된 원소가 존재하지 않는다는 것을, 각 원소들은 하나의 집합에만 속함을 의미하므로, 모든 원소들은 자신이 속해있는 유일한 집합만을 가지게 됩니다.

Disjoint set data structure를 사용하면 서로 다른 원소들이 같은 집합에 속해있는지, 혹은 속해있지 않은지를 판별하는데에 유용히 사용할 수 있습니다.

이를 활용하기 위해서는 Disjoint Set Union(DSU, 분리합집합) 자료구조를 만들 수 있어야 한다.

정의에 의해 Disjoint Set 사이에는 교집합이 없기 때문에, 합 연산을 하는 과정에서 두 집합 사이의 겹치는 원소를 특별히 고려하지 않고 모든 원소들을 하나의 집합으로 합치는 것이 가능합니다. 이 합하는 과정을 매우 빠르게, 그리고 각 원소들이 어떠한 집합 속에 있는지 판별하는 과정을 매우 빠르게 하기 위해서 Disjoint Set Union을 사용합니다.

Disjoint Set은 트리를 이용하여 표현하게 됩니다. 같은 집합에 속한 원소들 중 하나를 루트로 하고, 나머지 원소들을 각각 루트 원소의 자식이 되도록 표현하는 것을 기본으로 합니다.

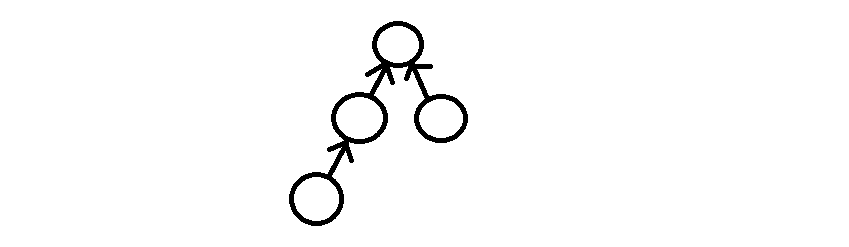
트리를 구성하는 과정에서는 자식 노드만 자신의 부모 노드가 누구인지 알고 있으면 됩니다.

트리를 구성하는 이유는 해당 트리에 속해있는 루트 노드를 그 집합을 대표하는 노드로 놓아, 한 원소가 어떤 집합에 속해있는지 확인하는 과정을 해당 원소가 자신이 속한 트리의 루트 노드가 누구인지 확인하는 과정을 통해 판별하기 때문입니다. (같은 트리에 속한 원소들은 루트가 다 같으며, 원소의 루트가 다를 경우 다른 트리에 속한다는 것이 분명합니다.)

이 과정에서 우리는 부모 노드가 누구인지 알고 있다면, 계속해서 부모 노드를 따라가다가 결국에는 루트 노드를 만나 자신이 어디에 속해있는지 확인할 수 있습니다.

즉, 우리는 실제로 그래프를 표현하는 방법을 통해 트리를 표현할 필요는 없으며, 그저 자신의 부모노드가 누구인지 기록하는 배열을 통해서 서로소 집합을 구현하는 것이 가능합니다.

어떤 두 원소가 같은 집합에 속해있는지 판별하기 위해서는, 위 그림과 같이 서로소 집합을 트리로 표현한 이후, 비교할 원소들 각각의 부모를 찾아가면서 루트 노드를 구하고, 해당 루트 노드가 같은지를 비교하여 서로 같은 집합에 속해있는지 판별할 수 있습니다.

Union & Find

연산 과정에서, 서로 달랐던 두 서로소 집합에 대한 합연산(Union)을 구현해야할 수도 있습니다. 서로소 집합 사이엔 공통 원소가 없으므로, 하나로 합치기 위해서는 위와 같이 표현한 두 집합(트리) 중 하나를 다른 한 쪽 트리에 합치는 것으로 구현합니다.

이 때, 두 개의 트리를 하나로 합치는 방법은 굉장히 다양할 수 있지만, 우리는 많은 경우, 한 쪽 트리의 루트 노드를 다른 쪽 트리의 루트 노드의 자식으로 합치는 방식을 사용합니다.

• 각각의 원소, 또는 일부를 다른 트리에 합하는 과정은 루트 노드 하나의 부모를 변경하는 일보다 더 많은 연산이 필요합니다.
• A 트리의 루트 노드를 B트리의 임의의 노드의 자식으로 만드는 일은, A 트리의 원소들이 루트 노드를 찾기 위해 부모 노드를 확인하는 연산의 수를 기존의 방식보다 더 늘리게 됩니다. 루트 노드에 바로 합친다면 A의 모든 원소들은 기존보다 한 번의 연산을 더 하면 되지만, B의 루트 노드가 아닌 노드에 합칠 경우 최소 2회 이상의 연산을 더 해야합니다.

이와 같이 한 쪽 트리의 루트 노드의 부모를 바꾸는 경우, 자식으로 합쳐진 트리의 새로운 루트는 자식으로 합쳐지지 않은 다른 트리의 루트가 됨을 알 수 있습니다. 즉, 두 트리의 합 트리의 모든 원소들의 루트는 합 트리의 루트와 같다는 것을 알 수 있고, 이는 두 집합이 합쳐진 것과 같음을 알 수 있습니다.

집합을 트리로 구현하여 표현하면 분리집합을 판별할 수 있고, 이를 합하는 과정 또한 해결할 수 있습니다. 하지만 이처럼만 판별하면 문제가 생기는데, 바로 트리 내에서 원소들의 편중이 일어날 수 있다는 것입니다.

앞서 트리를 합치는 과정을 생각할 때에, 우리는 서로소 집합을 구현할때에 어디에서 시간 효율성을 고려해야하는지 알 수 있었습니다.

• 서로소 집합에서 부모 노드를 확인해가면서, 루트 노드가 무엇인지 찾기(Find)

서로소 집합에서는 항상 어떤 원소가 어느 집합에 속해있는지에 대한 정보를 알아내는 것이 중요하여, 이를 빠르게 해결할 수 있도록 자료구조를 만들어주는 것이 중요합니다.

다음과 같은 경우를 생각해봅시다.

N개의 원소들이 각각 서로 다른 집합에 속해있습니다. 이 때, 어떤 두 트리를 합쳐가는 과정에서, 1번을 2번의 자식으로 합치게 되고, 이후 2번을 3번의 자식으로, 3번을 4번과 같이 N번 원소까지 합쳐나간다면, 우리는 N - N-1 - N-2 - … - 2 - 1 번 원소가 한 줄로 이어진 선형 트리가 생길 수도 있습니다.

이러한 최악의 경우, 1번 원소에서는 한 번 루트를 찾을 때에 2번부터 N번까지의 부모를 모두 다 확인하면서 찾아가기 때문에 최악에 O(트리의 크기) 만큼의 시간이 걸릴 수 있습니다.

두 트리를 합칠 때에, 항상 루트 노드를 루트 노드의 자식으로 만든다는 것이 다른 방법보다는 더 좋은 방법이지만, 위와 같은 경우처럼 최악의 선형 트리가 생기는 경우를 막을 수는 없습니다.

이러한 문제를 해결하기 위해 다음과 같은 2가지 방법이 등장하게 됩니다.

1. 경로 압축 (Path Compression)

Path Compression은 집합 내 한 원소에서 루트를 찾는 과정을 압축시키는 방법입니다. 원소에서 부모를 향해가면서 원소와 루트 사이의 모든 원소들을 방문합니다. 이 과정에서 원소와 루트 사이에 방문한 모든 원소들의 루트 또한 현 원소에서의 루트와 같다는 것을 알 수 있습니다. 결국, 한 경로를 찾아가는 과정에서 방문한 모든 원소의 부모를 루트로 갱신해줍니다. 이를 통해서 경로에 존재하는 모든 원소의 부모가 바로 루트로 이어지게 만들 수 있습니다.

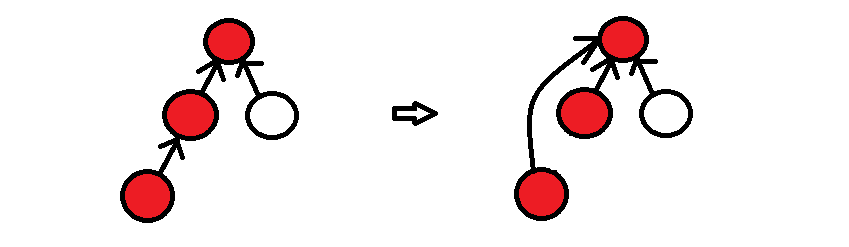
위 그림에서, 왼쪽 가장 아래의 원소에서 부모를 찾아가며 확인하게 되는 붉은 원소들의 부모 노드를, 모두 다 해당 루트 노드로 바꿔주게되면, 이후 해당 경로에 있는 원소들의 경우 부모 노드를 통해 바로 루트 노드에 접근할 수 있습니다.

이렇게 되면 처음에 확인할 경우에는 경로 상의 모든 노드들을 확인해야하지만, 그 이후에 확인할 때에는 O(1)만에 확인할 수 있게 되어 많은 find 연산을 진행할 때에 유리해집니다.

N개의 원소를 union하는 과정과, N 이상의 find를 하는 과정에서, 최악의 경우 평균적으로 한 번의 find 연산 당 O(log N)의 시간이 걸릴 수 있다는 것이 증명되어있습니다. (Worst-case Analysis of Set Union Algorithms, Robert E. Tarjan & Jan van Leeuwen, 1984)

2. 랭크 압축 (Rank Compression)

Rank Compression은 합하는 과정을 향상시키므로 이후 한 원소에서 루트를 찾아가는 경로 자체를 줄일 수 있는 방법입니다. 우리가 기존에 이야기한 것처럼 합치는 과정에서 한 트리의 루트를 다른 트리의 루트의 자식으로만 합하며, 이 과정에서 불필요한 경로를 단축할 수 있습니다. 그리고 더 중요한 압축 방법이 있는데, 많이 사용되는 방법은 두 가지가 있습니다.

1. 트리의 깊이가 더 작은 쪽을 큰 쪽에 합한다.

2. 트리의 크기가 더 작은 쪽을 큰 쪽에 합한다.

1번의 경우, 깊이가 더 작은 쪽을 큰 쪽에 합하는 것으로, 두 트리를 합치면서 깊이가 깊어지는 상황에는 깊이가 1 증가하고, 그 과정에서 합한 트리의 크기는 둘 중 더 작은 트리의 크기의 2배 이상 증가하게 됩니다.

이를 통하여 최악의 경우로 원소의 수 대비 깊이가 가장 깊어지도록 만들어봅시다. (하나의 원소만 있을 때에 해당하는 깊이를 편의상 1이라 하겠습니다)

맨 처음에는 1개의 원소를 1개의 원소로 합쳐 깊이가 1 증가하며 크기는 2가 된다는 사실을 알 수 있습니다. 즉, 깊이가 2인 최소 원소의 수는 2개가 됩니다.

깊이가 3인 트리를 만들기 위해서는 깊이가 2인 트리 2개가 필요합니다. 해당 조건을 만족하는 최소 원소의 수가 2이므로, 크기가 2인 트리 2개를 합쳐 깊이가 3이며 크기가 4인 트리를 만들 수 있습니다.

이처럼 해당 깊이에 대해 원소의 수가 가장 작은 트리 2개를 합하게 되면 항상 크기는 최소 2배씩 커진다는 사실을 알 수 있습니다. (1, 2, 4, 8…)

즉, 최악의 경우 항상 깊이 대비 최소 원소의 수를 가지는 트리를 합쳐 만들어지게 되면, 높이는 약 완전 이진트리의 높이와 같은 lg N이 되어, 하나의 경로를 살펴보는 find 과정에서 최악에 O(log N)의 시간이 소비됩니다.

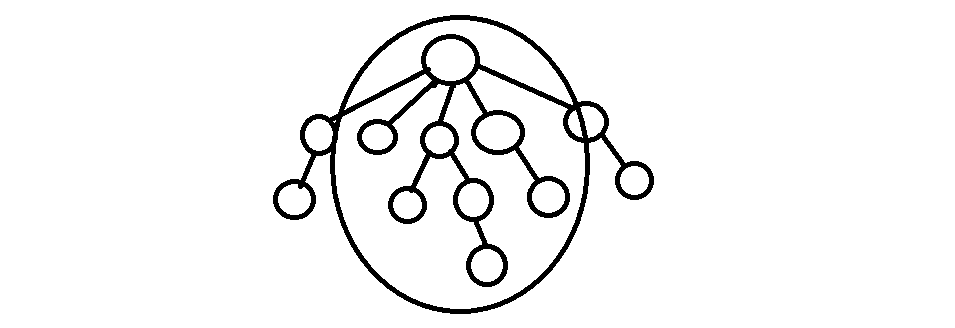
최악의 깊이 증가가 있기 위해서는 같은 깊이의 최소 크기 트리가 필요하다 - 깊은 부분은 완전 이진트리에 가까워진다.

2번의 경우도 1번과 비슷한 방식으로, 최악에 트리의 높이가 O(log N)이 된다는 사실을 증명할 수 있습니다.

이번에는 ‘깊이가 a이기 위해서는 크기가 최소 b 이상이 된다’ 는 정보를 통해 최악의 경우를 만들어보겠습니다.

깊이가 1, 크기가 1인 트리 2개를 합치는 경우에 우리는 깊이가 2, 크기가 2인 트리를 만들어낼 수 있습니다. 즉, 깊이가 2이기 위해서는 크기가 최소 2 이상이어야 함을 알 수 있습니다.

트리의 깊이를 증가시키기 위해서는, 해당 깊이를 가지는 최소 트리가 같은 깊이를 가지며 그것보다 더 크기가 크거나 같은 다른 트리에 합쳐지면서 생기는 경우가 유일합니다.

즉, 깊이를 증가시키며 크기가 최소로 되기 위해서는 결국 같은 깊이의 최소 크기를 가지는 트리 2개를 합치는 경우가 최악의 경우가 된다는 것을 어렵지 않게 알 수 있습니다.

결국 깊이 3인 트리를 만들기 위해서는 크기가 2인 트리 2개를 합쳐 4인 크기의 트리를 만들어야하며, 그 이후로는 4인 트리 2개를 합쳐 크기가 8인 트리를 만드는 것이 깊이가 4인 최소 트리임을 알 수 있어, 앞선 경우와 같이 깊이 1이 커질 경우 크기는 2배씩 커지는 경우가 최악임을 알 수 있습니다.

이를 통해 1번의 경우와 같이, N개의 원소를 가지는 집합의 최대 높이는 약 log N 임을 알 수 있어, find 과정의 시간복잡도가 O(log N)이 됩니다.

3. Path Compression + Rank Compression

Path Compression과 Rank Compression을 둘 다 이용할 경우, DSU의 시간복잡도는 O(α(N))이라는 것이 증명되어있습니다.(Efficiency of a Good But Not Linear Set Union Algorithm, Robert Tarjan, 1975) α(N)은 에커먼 함수의 역함수인데, 거의 상수에 가깝게 동작한다고 볼 수 있습니다. 에커먼 함수의 계산량에 관련된 정보는 링크를 통해 확인하실 수 있습니다.

Rank Compression을 사용하지 않을 경우, 랜덤한 데이터에서는 Path Compression 만으로도 충분히 빠른 시간에 동작하며, 최악의 경우도 O(log N)이기 때문에 일반적인 경우의 구현은 Path Compression만 이용해도 괜찮은 경우가 많아 문제 해결을 위한 프로그래밍을 하는 과정에서, Rank Compression을 사용하지 않는 경우도 흔합니다.

하지만 만약에 합쳐진 경로가 중요하여 주어진 트리 구조를 망가뜨리는 것이 불가능한 경우, Path Compression을 사용하는 것이 불가능하므로, 이 경우에는 Rank Compression을 이용하여 O(log N)의 시간복잡도를 보장받을 수 있습니다.

코드

Disjoint Set - Union & find

int parent[n + 1] = {0, 1, ..., n};

int find(int a){
 if(a == parent[a]) return a;
 return find(parent[a]);
}
void union(int a, int b){
 a = find(a);
 b = find(b);
 parent[b] = a;
}

path compression

int find(int a){
 if(a == parent[a]) return a;
 return parent[a] = find(parent[a]);
}

rank compression(by using size)

int rank[n + 1] = {1, 1, ..., 1};

void union(int a, int b){
 a = find(a);
 b = find(b);
 if(rank[a] < rank[b]) swap(a, b);
 rank[a] += rank[b];
 parent[b] = a;
}

현재 c++ 버전에 따라 rank를 변수명으로 사용할 수 없을 수도 있으니, 이를 고려하여 변수명을 바꾸어 사용하시면 됩니다.