Li Chao Tree의 Lazy Propagation

data-structure

개요

리차오 트리는 직선들을 관리하는 동적 세그먼트 트리의 일종으로, Convex Hull Trick 등등에서 쓰이는 자료구조입니다.

다른 세그먼트 트리와 마찬가지로 리차오 트리에도 레이지 프로퍼게이션을 적용할 수 있지만, 이에 대해서는 잘 알려져 있지 않습니다.

이 글에서는 리차오 트리에 레이지 프로퍼게이션을 적용한 확장 연산들과 그 활용에 대해 소개합니다.

리차오 트리

좌표 범위가 $N$일 때, 기본적인 리차오 트리는 다음과 같은 연산들을 할 수 있습니다.

insert(a,b) : 새로운 직선 $y=ax+b$를 삽입한다. $O(\log{N})$
get(x) : 주어진 $x$좌표에서 $y$좌표의 최솟값을 구한다. $O(\log{N})$

잘 알려진 자료구조이므로 설명은 생략하겠습니다. 다음 글에서 리차오 트리를 배울 수 있습니다.

선분 삽입

insert 함수를 조금만 수정하면 직선을 원하는 구간에만 삽입하는 것도 가능합니다.

insert(l,r,a,b) : $[l,r]$ 구간에 새로운 선분 $y=ax+b$를 삽입한다. $O(\log^2{N})$

일반적인 세그먼트 트리처럼 $[l,r]$ 구간을 $O(\log{N})$개의 노드로 쪼갠 뒤, 각각의 노드에 직선 삽입 연산을 적용하면 됩니다.

위 기능들을 지원하는 리차오 트리의 구현체는 다음과 같습니다.

#define ll long long
const ll inf = 4e18;
struct LiChao {
	struct Node { // 리차오 트리의 노드 구조체
		int l, r; // l,r은 각각 왼쪽,오른쪽 자식의 노드 번호
		ll a, b; // 직선 y = ax + b
		Node() { l = 0; r = 0; a = 0; b = inf; }
	};
	vector<Node> seg; // 새로운 노드가 생성될 때마다 여기에 push_back
	ll _l, _r;
	LiChao(ll l, ll r) {
		seg.resize(2); // 0번은 더미 노드, 1번은 루트 노드
		_l = l; _r = r; // 관리할 전체 구간
	}
	void insert(ll L, ll R, ll a, ll b, int n, ll l, ll r) {
		// [L,R] 구간에 직선 y = ax + b를 삽입하려는데,
		// 현재 보고 있는 노드 n이 관리하는 구간이 [l,r]인 상황.
		
		if (r < L || R < l || L > R) return; // 삽입하려는 구간을 완전히 벗어난 경우
		
		if (l != r) { // 왼쪽 자식이나 오른쪽 자식이 없다면 만들어 준다.
			if (seg[n].l == 0) seg[n].l = seg.size(), seg.push_back(Node());
			if (seg[n].r == 0) seg[n].r = seg.size(), seg.push_back(Node());
		}

		ll m = l+r>>1;
		if (l < L || R < r) { // 삽입하려는 구간에 걸치는 경우
			// 이러한 경우는 O(logN)개 존재한다.
			// 왼쪽 구간과 오른쪽 구간으로 재귀적으로 분할한다.
			if (L <= m) insert(L, R, a, b, seg[n].l, l, m);
			if (m+1 <= R) insert(L, R, a, b, seg[n].r, m+1, r);
			return;
		}

		// 삽입하려는 구간에 완전히 포함되는 경우
		// 이러한 경우는 O(log^2 N)개 존재한다.
		ll &sa = seg[n].a, &sb = seg[n].b;
		if (a*l+b < sa*l+sb) swap(a, sa), swap(b, sb); // 일반성을 잃지 않고, 구간의 맨 왼쪽을 지배하는 직선이 y = sa*x + sb가 되게 한다.
		if (a*r+b >= sa*r+sb) return; // 한 직선이 다른 직선보다 항상 아래에 있는 경우

		if (a*m+b < sa*m+sb) { // 오른쪽 절반을 y = a*x + b가 전부 지배
			swap(a, sa), swap(b, sb);
			insert(L, R, a, b, seg[n].l, l, m);
		}
		else // 왼쪽 절반을 y = sa*x + sb가 전부 지배
			insert(L, R, a, b, seg[n].r, m+1, r);
	}
	ll get(ll x, int n, ll l, ll r) {
		if (n == 0) return inf; // 노드가 존재하지 않는 경우
		ll ret = seg[n].a*x + seg[n].b, m = l+r>>1;
		if (x <= m) return min(ret, get(x, seg[n].l, l, m));
		return min(ret, get(x, seg[n].r, m+1, r));
	}
	void insert(ll L, ll R, ll a, ll b) {
		insert(L, R, a, b, 1, _l, _r);
	}
	ll get(ll x) {
		return get(x, 1, _l, _r);
	}
};

확장된 리차오 트리

레이지 프로퍼게이션을 적용한, 확장된 리차오 트리는 다음과 같은 연산들을 할 수 있습니다.

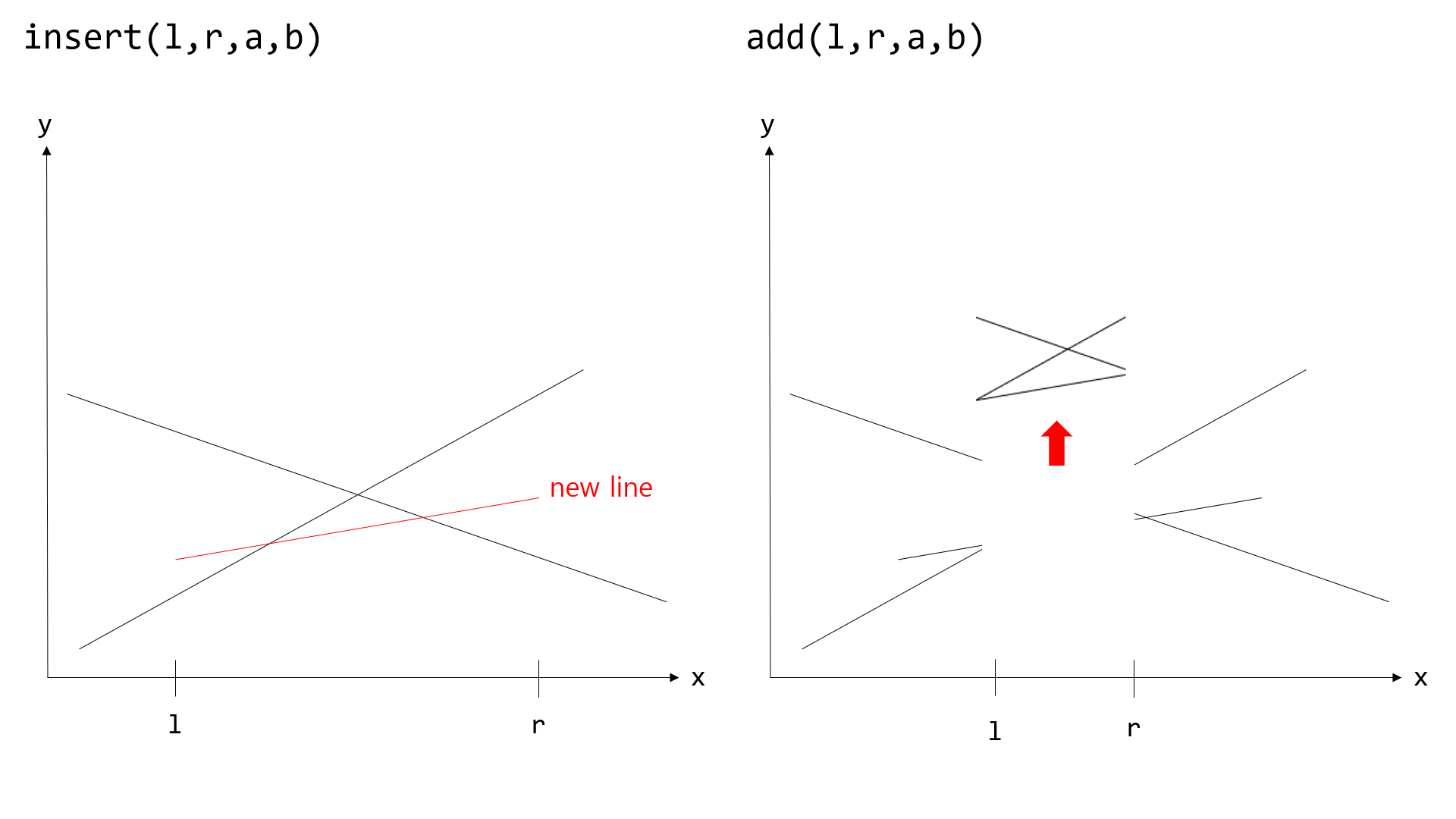
insert(l,r,a,b) : $[l,r]$ 구간에 새로운 선분 $y=ax+b$를 삽입한다. $O(\log^2{N})$
add(l,r,a,b) : $[l,r]$ 구간에 선분 $y=ax+b$를 더한다. $O(\log^2{N})$
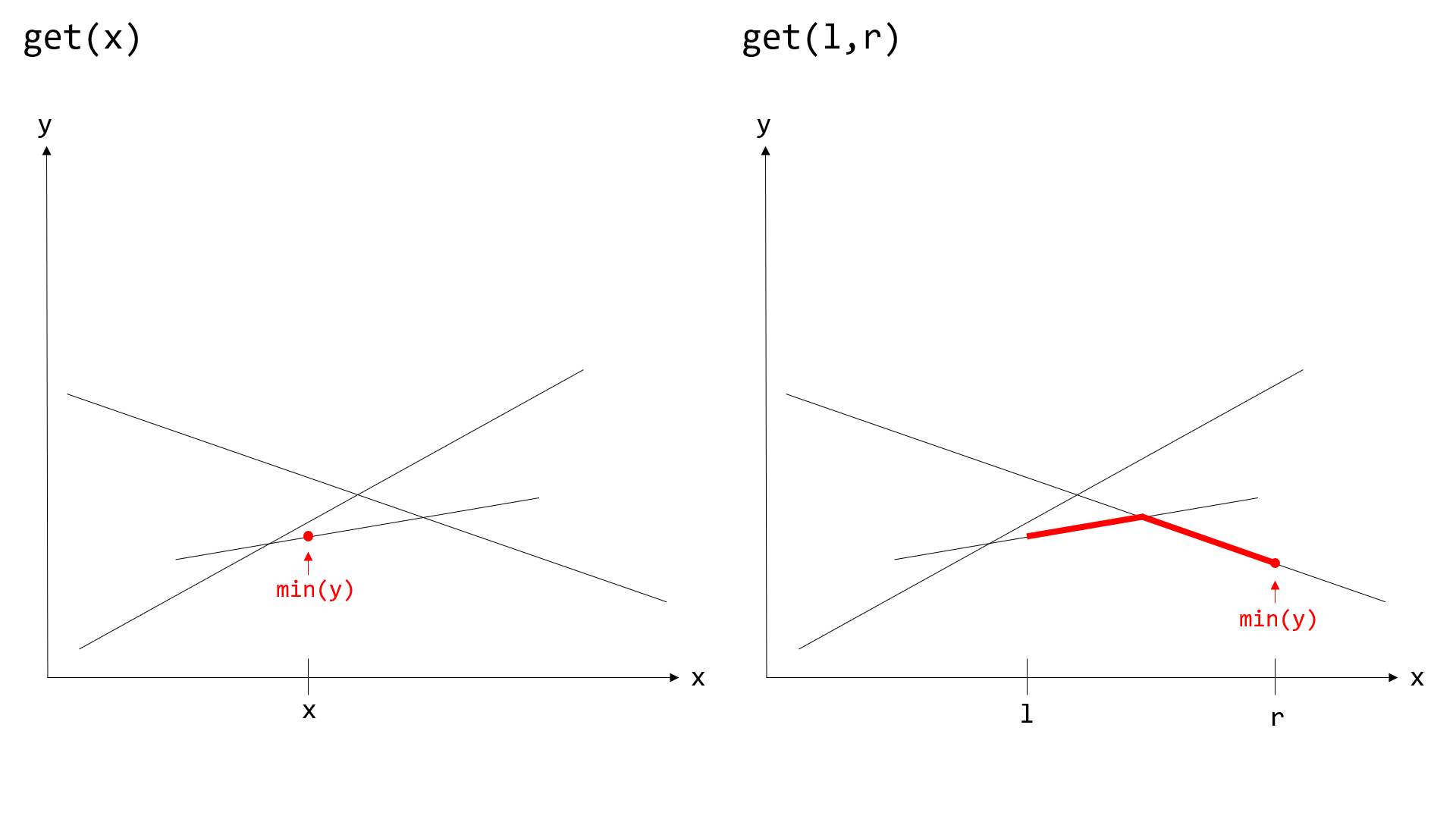
get(x) : 주어진 $x$좌표에서 $y$좌표의 최솟값을 구한다. $O(\log{N})$
get(l,r) : $l \leq x \leq r$인 $x$좌표들 중 $y$좌표의 최솟값을 구한다. 단, 이 함수가 올바르게 작동하려면 $a \neq 0$인 add 함수를 호출한 적이 없어야 한다. $O(\log{N})$

레이지 프로퍼게이션

일반 세그먼트 트리의 레이지 프로퍼게이션과 원리는 같지만, 리차오 트리라서 발생하는 문제점이 하나 있습니다.

위 그림에서 회색 노드들이 관리하는 선분은 부분적으로만 더해지기 때문에 관리하기가 까다롭습니다.

이에 대한 해결책으로, 회색 노드가 관리하는 구간이 $[l,r]$이고 $m = \left \lfloor \frac{l+r}{2} \right \rfloor$일 때, 회색 노드의 선분을 $[l,m]$과 $[m+1,r]$ 두 구간으로 분할한 뒤 insert 연산으로 다시 삽입하는 방법이 있습니다.

분할 삽입 과정을 마치면 회색 노드들은 아무런 선분도 갖고 있지 않으므로, 이들을 신경쓰지 않고 레이지 프로퍼게이션을 적용할 수 있습니다.

회색 노드의 개수가 $O(\log{N})$개이고 분할 삽입 한 번마다 $O(\log{N})$의 시간이 들기 때문에, 전체 분할 삽입 과정의 시간복잡도는 $O(\log^2{N})$이 됩니다.

구간 쿼리

일반적인 세그먼트 트리처럼 각 노드마다 서브트리의 최솟값을 관리한다면 구간 쿼리를 할 수 있습니다.

$[l,r]$ 구간에 새로운 선분이 삽입될 때, 이 선분의 y좌표 최솟값은 $x=l$ 또는 $x=r$에 존재하므로 둘 중 작은 값으로 갱신하면 됩니다.

아무 때에나 적용되는 것은 아니고 제약이 있는데, 구간 쿼리를 하려면 add 함수에서 기울기를 더한 적이 없어야 합니다. 선분의 기울기가 변하면서 최솟값의 위치가 달라지면 구간 최솟값을 관리할 수 없기 때문입니다.

구현

먼저 노드 구조체에 서브트리 최솟값과 레이지 값들을 추가합니다.

struct Node {
	int l, r;
	ll a, b;
	ll mn; // 서브트리의 최솟값
	ll aa, bb; // 레이지 값들. a += aa, b += bb
	Node() { l = 0; r = 0; a = 0; b = inf; mn = inf; aa = 0; bb = 0; }
};

다음으로 레이지 값들을 전파하는 propagate 함수를 추가합니다.

void propagate(int n, ll l, ll r) {
	if (seg[n].aa || seg[n].bb) {
		if (l != r) { // 자식들로 전파
			if (seg[n].l == 0) seg[n].l = seg.size(), seg.push_back(Node());
			if (seg[n].r == 0) seg[n].r = seg.size(), seg.push_back(Node());
			seg[seg[n].l].aa += seg[n].aa, seg[seg[n].l].bb += seg[n].bb;
			seg[seg[n].r].aa += seg[n].aa, seg[seg[n].r].bb += seg[n].bb;
		}
		// 현재 노드 업데이트
		seg[n].mn += seg[n].bb;
		seg[n].a += seg[n].aa, seg[n].b += seg[n].bb;
		seg[n].aa = seg[n].bb = 0;
	}
}

기존에 있던 insert와 get 함수에서도 레이지 값과 서브트리 최솟값을 관리해 주어야 합니다.

void insert(ll L, ll R, ll a, ll b, int n, ll l, ll r) {
	if (r < L || R < l || L > R) return;
	propagate(n, l, r);
	seg[n].mn = min({seg[n].mn, a*max(l,L)+b, a*min(r,R)+b});
	...
}
ll get(ll x, int n, ll l, ll r) {
	if (n == 0) return inf;
	propagate(n, l, r);
	...
}

다음으로 add 함수를 추가합니다. insert와 유사하게 구현할 수 있습니다.

void add(ll L, ll R, ll a, ll b, int n, ll l, ll r) {
	// [L,R] 구간에 직선 y = ax + b를 더하려는데,
	// 현재 보고 있는 노드 n이 관리하는 구간이 [l,r]인 상황.

	if (r < L || R < l || L > R) return; // 더하려는 구간을 완전히 벗어난 경우
	if (seg[n].l == 0) seg[n].l = seg.size(), seg.push_back(Node());
	if (seg[n].r == 0) seg[n].r = seg.size(), seg.push_back(Node());
	propagate(n, l, r);
	ll m = l+r>>1;

	if (l < L || R < r) { // 더하려는 구간에 걸치는 경우
		// 분할 삽입
		insert(l, m, seg[n].a, seg[n].b, seg[n].l, l, m);
		insert(m+1, r, seg[n].a, seg[n].b, seg[n].r, m+1, r);
		seg[n].a = 0, seg[n].b = inf, seg[n].mn = inf; // 노드 비우기

		// 왼쪽 구간과 오른쪽 구간에서 재귀적으로 진행
		if (L <= m) add(L, R, a, b, seg[n].l, l, m);
		if (m+1 <= R) add(L, R, a, b, seg[n].r, m+1, r);
		
		// 서브트리 최솟값 갱신
		seg[n].mn = min(seg[seg[n].l].mn, seg[seg[n].r].mn);
		return;
	}

	// 더하려는 구간에 완전히 포함되는 경우
	seg[n].aa += a, seg[n].bb += b;
	propagate(n, l, r);
}

마지막으로 구간 쿼리를 하는 get 함수를 추가합니다. 세그먼트 트리의 구간 쿼리와 유사하게 구현하는데, 구간에 걸친 노드 안의 선분도 고려해야 합니다.

ll get(ll L, ll R, int n, ll l, ll r) {
	if (n == 0) return inf;
	if (r < L || R < l || L > R) return inf; // 구간을 완전히 벗어난 경우
	propagate(n, l, r);
	if (L <= l && r <= R) return seg[n].mn; // 구간에 완전히 포함되는 경우
	ll m = l+r>>1;
	// 구간에 걸치는 경우
	return min({seg[n].a*max(l,L)+seg[n].b, seg[n].a*min(r,R)+seg[n].b, get(L, R, seg[n].l, l, m), get(L, R, seg[n].r, m+1, r)});
}

최종 코드는 다음과 같습니다.

#define ll long long
const ll inf = 4e18;
struct LiChao {
	struct Node {
		int l, r; ll a, b, mn, aa, bb;
		Node() { l = 0; r = 0; a = 0; b = inf; mn = inf; aa = 0; bb = 0; }
	};
	vector<Node> seg;
	ll _l, _r;
	LiChao(ll l, ll r) {
		seg.resize(2);
		_l = l; _r = r;
	}
	void propagate(int n, ll l, ll r) {
		if (seg[n].aa || seg[n].bb) {
			if (l != r) {
				if (seg[n].l == 0) seg[n].l = seg.size(), seg.push_back(Node());
				if (seg[n].r == 0) seg[n].r = seg.size(), seg.push_back(Node());
				seg[seg[n].l].aa += seg[n].aa, seg[seg[n].l].bb += seg[n].bb;
				seg[seg[n].r].aa += seg[n].aa, seg[seg[n].r].bb += seg[n].bb;
			}
			seg[n].mn += seg[n].bb;
			seg[n].a += seg[n].aa, seg[n].b += seg[n].bb;
			seg[n].aa = seg[n].bb = 0;
		}
	}
	void insert(ll L, ll R, ll a, ll b, int n, ll l, ll r) {
		if (r < L || R < l || L > R) return;
		if (seg[n].l == 0) seg[n].l = seg.size(), seg.push_back(Node());
		if (seg[n].r == 0) seg[n].r = seg.size(), seg.push_back(Node());
		propagate(n, l, r);
		seg[n].mn = min({seg[n].mn, a*max(l,L)+b, a*min(r,R)+b});
		ll m = l+r>>1;
		if (l < L || R < r) {
			if (L <= m) insert(L, R, a, b, seg[n].l, l, m);
			if (m+1 <= R) insert(L, R, a, b, seg[n].r, m+1, r);
			return;
		}
		ll &sa = seg[n].a, &sb = seg[n].b;
		if (a*l+b < sa*l+sb) swap(a, sa), swap(b, sb);
		if (a*r+b >= sa*r+sb) return;
		if (a*m+b < sa*m+sb) {
			swap(a, sa), swap(b, sb);
			insert(L, R, a, b, seg[n].l, l, m);
		}
		else insert(L, R, a, b, seg[n].r, m+1, r);
	}
	void add(ll L, ll R, ll a, ll b, int n, ll l, ll r) {
		if (r < L || R < l || L > R) return;
		if (seg[n].l == 0) seg[n].l = seg.size(), seg.push_back(Node());
		if (seg[n].r == 0) seg[n].r = seg.size(), seg.push_back(Node());
		propagate(n, l, r);
		ll m = l+r>>1;
		if (l < L || R < r) {
			insert(l, m, seg[n].a, seg[n].b, seg[n].l, l, m);
			insert(m+1, r, seg[n].a, seg[n].b, seg[n].r, m+1, r);
			seg[n].a = 0, seg[n].b = inf, seg[n].mn = inf;
			if (L <= m) add(L, R, a, b, seg[n].l, l, m);
			if (m+1 <= R) add(L, R, a, b, seg[n].r, m+1, r);
			seg[n].mn = min(seg[seg[n].l].mn, seg[seg[n].r].mn);
			return;
		}
		seg[n].aa += a, seg[n].bb += b;
		propagate(n, l, r);
	}
	ll get(ll x, int n, ll l, ll r) {
		if (n == 0) return inf;
		propagate(n, l, r);
		ll ret = seg[n].a*x + seg[n].b, m = l+r>>1;
		if (x <= m) return min(ret, get(x, seg[n].l, l, m));
		return min(ret, get(x, seg[n].r, m+1, r));
	}
	ll get(ll L, ll R, int n, ll l, ll r) {
		if (n == 0) return inf;
		if (r < L || R < l || L > R) return inf;
		propagate(n, l, r);
		if (L <= l && r <= R) return seg[n].mn;
		ll m = l+r>>1;
		return min({seg[n].a*max(l,L)+seg[n].b, seg[n].a*min(r,R)+seg[n].b, get(L, R, seg[n].l, l, m), get(L, R, seg[n].r, m+1, r)});
	}
	void insert(ll L, ll R, ll a, ll b) {
		insert(L, R, a, b, 1, _l, _r);
	}
	void add(ll L, ll R, ll a, ll b) {
		add(L, R, a, b, 1, _l, _r);
	}
	ll get(ll x) {
		return get(x, 1, _l, _r);
	}
	ll get(ll L, ll R) {
		return get(L, R, 1, _l, _r);
	}
};

연습 문제

반평면 땅따먹기

기존의 리차오 트리로 할 수 있는 것들은 확장된 리차오 트리로도 할 수 있습니다.

구현체가 최솟값 버전이므로 최댓값을 구하기 위해서는 부호에 음수를 붙여야 함에 유의합시다.

리차오 트리를 생략한 코드는 아래와 같습니다.

#include<bits/stdc++.h>
using namespace std;

int Q;

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
	LiChao tree(-1e12, 1e12);
	cin >> Q;
	while(Q--) {
		ll t, a, b, x;
		cin >> t;
		if (t == 1) {
			cin >> a >> b;
			tree.insert(-1e12, 1e12, -a, -b);
		}
		else {
			cin >> x;
			cout << -tree.get(x) << "\n";
		}
	}
	return 0;
}

AtCoder Beginner Contest 177 F. I hate Shortest Path Problem

$f(i,j)$를 1행에서 $(i,j)$로 가는 최소 이동 횟수라고 정의합시다.

$f(i,\ast)$에서 $f(i+1,\ast)$로 가는 상태 전이는 다음과 같습니다.

$j < A_{i}$ 또는 $j > B_{i}$에서 $f(i+1,j) := f(i,j)+1$
$A_{i} \leq j \leq B_{i}$에서,
- $A_{i} = 1$이면 $f(i+1,j) := \infty$
- $A_{i} > 1$이면 $f(i+1,j) := f(i+1,A_{i}-1) + j - (A_{i}-1)$

구간에 직선을 더하거나 삽입하면서 구간 최솟값을 구할 수 있어야 하므로, 확장된 리차오 트리로 $O(H\log^2{W})$에 해결할 수 있습니다.

코드는 다음과 같습니다.

#include<bits/stdc++.h>
using namespace std;

int H, W;

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
	cin >> H >> W;
	LiChao tree(1, W);
	tree.insert(1, W, 0, 0);
	for(int i=1; i<=H; i++) {
		int l, r;
		cin >> l >> r;
		tree.add(1, W, 0, 1);
		tree.add(l, r, 0, 1e9);
		if (l-1 >= 1) {
			ll x = tree.get(l-1);
			tree.insert(l, r, 1, x-(l-1));
		}
		ll res = tree.get(1, W);
		if (res >= 1e9) res = -1;
		cout << res << "\n";
	}
	return 0;
}

Codeforces Round #371. Sonya and Problem Without a Legend

$O(N^2)$ DP로 풀 수 있지만, $O(N\log{N})$ Slope Trick(설명+풀이) 으로도 풀 수 있습니다.

링크한 글의 풀이처럼 우선순위 큐로 기울기가 변하는 지점들을 관리하는 방법이 주로 알려져 있는데, 함수 개형을 그대로 확장된 리차오 트리에 넣어서 관리할 수도 있습니다.

기울기 덧셈을 하기 때문에 get(l,r)은 사용할 수 없지만, 보통 Slope Trick에서 관리하는 함수는 볼록하기 때문에 구간 최솟값 쿼리를 삼분 탐색으로 구할 수 있습니다.

링크한 글의 풀이를 확장된 리차오 트리로 $O(N\log^2{\max{a_i}})$에 구현한 코드는 다음과 같습니다.

#include<bits/stdc++.h>
using namespace std;

int N;
int A[3001];

pair<ll, ll> ternary_search(LiChao &tree) {
	ll lo = 0, hi = 1e9+N;
	for(int i=0; i<30; i++) { // 기울기에 대한 이분 탐색
		ll mid = lo+hi>>1;
		if (tree.get(mid) <= tree.get(mid+1)) hi = mid;
		else lo = mid;
	}
	return {hi, tree.get(hi)}; // {최솟값의 x좌표, 최솟값} pair 리턴
}

int main() {
	ios::sync_with_stdio(0); cin.tie(0);
	cin >> N;
	for(int i=1; i<=N; i++) {
		cin >> A[i];
		A[i] += N-i; // 조건을 monotonically increasing으로 바꾸기
	}
	LiChao tree(0, 1e9+N);
	tree.insert(0, 1e9+N, 0, 0);
	for(int i=1; i<=N; i++) {
		auto [x,y] = ternary_search(tree);
		tree.insert(x, 1e9+N, 0, y);
		tree.add(0, A[i], -1, A[i]);
		tree.add(A[i], 1e9+N, 1, -A[i]);
	}
	cout << ternary_search(tree).second << "\n";
	return 0;
}