Fast Polygon Triangulation

computational-geometry , triangulation , algorithm

Introduction
Preliminaries
Montone Polygon Triangulation
- Example
Polygon Triangulation
Implementation

Introduction

안녕하세요, Aeren입니다!

Polygon triangulation은 classical한 computational geometry problem중 하나로, 어떤 simple polygon의 boundary가 counterclockwise하게 주어질 때, triangulation을 찾는 문제입니다. 이번 글에서 소개할 내용은 $N$을 polygon의 vertex 갯수라고 할 때 $O(N \log N)$시간 안에 위 문제를 해결하는 알고리즘입니다. 참고로 이 문제는 $O(N)$시간 안에 해결 가능함이 알려져 있습니다. (참조)

Preliminaries

Degeneracy

이 글에서 모든 polygon은 simple하다고 가정합니다. 즉, 임의의 서로다른 두 edge들은 endpoint가 아닌 점에서 교점을 갖지 않으며 인접해 있지 않은 edge들은 끝점에서도 교차하지 않습니다. 또한 내각이 $\pi$인 vertex를 허용합니다. 하지만 인접한 두 vertex가 일치하는 것은 허용하지 않습니다.

Strict Total Order

Two dimensional euclidean space $\mathbb{R}^2$의 strict total order $<$를 “$(x,y)<(z,w)$ 이 성립할 필요충분조건은 $x< z$이거나 혹은 $x=z$이고 $y<w$이다.”로 정의하겠습니다.

Monotone Polygon

Polygon $P$가 주어질 때 (위 strict total order에 의한) unique한 minimum vertex $p$와 maximum vertex $q$가 존재합니다. 그리고 $P$의 boundary를 따라가는 $p-q$ path는 정확히 두개 존재합니다. $P$가 monotone하다는 것을 두 $p-q$ path 모두 증가하는 것으로 정의하겠습니다.

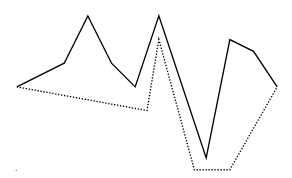
이 글에서 소개할 알고리즘은 주어진 polygon을 monotone polygon들로 분할한 뒤, 각 monotone polygon을 triangulate합니다.

Montone Polygon Triangulation

Monotone polygon의 경우 매우 간단한 linear time triangulation 알고리즘이 존재합니다.

Vertex들의 stack $S$를 준비합니다. $S$는 마지막에 삽입된 vertex가 upper $p-q$ path에 위치하는지의 여부에 따라 upper 혹은 lower configuration을 갖습니다.
주어진 polygon의 각 vertex들을 오름차순으로 스캔합니다.
$S$와 새로운 vertex의 configuration에 따라 두 가지 경우가 있습니다.
1. $S$의 configuration과 새로운 vertex $u$의 configuration이 다를 경우, 현재 $S$의 vertex들을 $v _ 1, \cdots, v_k$라고 할 때 각 $1 \le i < k$에 대하여 삼각형 $u, v _ i, v _ {i+1}$를 추가해준 후 $S:=\lbrace v_k,u \rbrace$로 놓습니다. (즉, $S$를 비워 준 후 $S$에 비우기 전 마지막 vertex와 새로운 vertex를 차례로 push합니다.)
2. $S$의 configuration과 새로운 vertex $u$의 configuration이 같을 경우, 현재 $S$의 vertex들을 $v _ 1, … , v _ k$라 하고, $p$를 $u, v _ {i-1}, v _ i$이 polygon 안에 놓이지 않는 가장 큰 $i$라 할 때, (그러한 $i$가 존재하지 않으면 $p=1$) 각 $p \le i < k$에 대하여 삼각형 $u, v _ i, v _ {i+1}$을 추가해 준 후, $S := \lbrace v _ 1, …, v _ p, u \rbrace$로 놓습니다.

Example

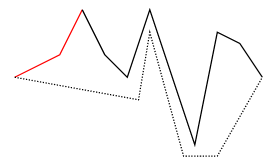
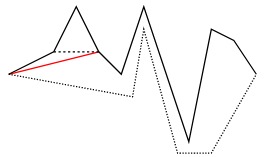
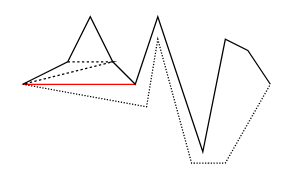
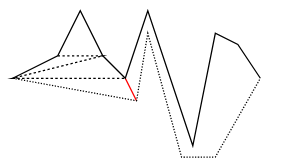
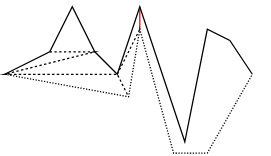
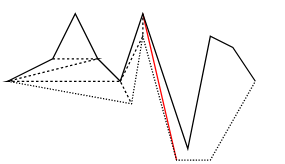
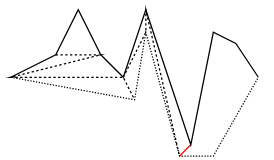
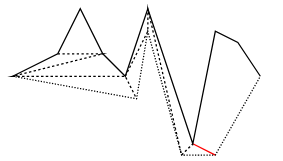
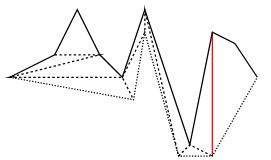
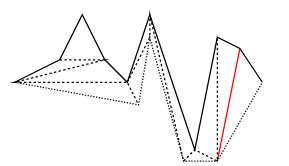
Polygon Triangulation

$O(n \log n)$시간안에 주어진 polygon을 monotone polygon들로 분할 할 수 있다면 각 monotone polygon을 위 알고리즘을 통해 $O(n)$시간 안에 triangulate함으로써 주어진 polygon을 triangulate할 수 있습니다.

Boundary Vertex Classification

Monotone polygon들로 분할하기에 앞서 boundary의 vertex들을 5가지로 분류하겠습니다.

Vertex $u$의 이웃한 두 vertex들을 $v,w$라고 하고, $u$의 내각을 $\theta$라고 할 때, $u$의 vertex type은 다음과 같이 정의됩니다.

Start Vertex: $u < \min(v,w)$ and $\theta < \pi$
Split Vertex: $u < \min(v,w)$ and $\theta > \pi$
End Vertex: $u > \max(v,w)$ and $\theta < \pi$
Merge Vertex: $u > \max(v,w)$ and $\theta > \pi$
Regular Vertex: None of the above

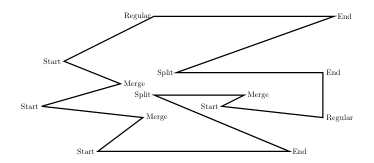
Monotone polygon에는 split vertex와 merge vertex가 존재하지 않습니다. 즉, 관건은 다음 figure와 같이 적당한 대각선을 추가하여 split vertex와 merge vertex를 없애는 것입니다.

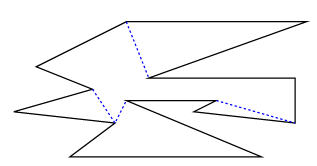
대각선을 추가하는 전략은 대략 다음과 같습니다. Split vertex의 경우, split vertex보다 작으면서 같은 monotone component에 속하는 가장 큰 vertex와 이어줍니다. Merge vertex의 경우, merge vertex보다 크면서 같은 monotone component에 속하는 가장 작은 vertex와 이어줍니다.

Sweepline Events

자세한 알고리즘은 다음과 같습니다.

Polygon의 각 점을 오름차순으로 스캔합니다.
교차하지 않는 선분들을 sweepline과의 교점을 기준으로 정렬된 상태로 저장하는 data structure $D$를 준비합니다. 각 선분은 현재 sweepline과 교차하는 monotone component의 위쪽 직선을 나타냅니다. 또한, 각 component마다 가장 최근에 스캔된 vertex를 저장합니다. (이 vertex를 helper라고 부르겠습니다.)
Sweepline이 vertex $u$에 도달했을때, $u$의 type에 따라 다음과 같이 $D$를 업데이트 해줍니다.
1. Start Vertex
  - $u$를 포함하는 새로운 component $C$를 $D$에 삽입하고 $\mathrm{helper}(C)$를 $u$로 놓습니다.
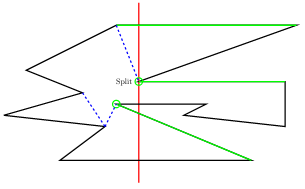
2. Split Vertex
  - $u$를 포함하는 component $C$를 찾습니다.
  - 대각선 $\mathrm{helper}(C)-u$를 추가합니다.
  - $C$를 $D$에서 삭제한 후, $u$를 기준으로 위쪽 component $U$와 아래쪽 component $L$로 분할하여 $D$에 삽입합니다.
  - $\mathrm{helper}(U)$와 $\mathrm{helper}(L)$을 $u$로 놓습니다.
3. End Vertex
  - $u$를 포함하는 component $C$를 찾습니다.
  - $\mathrm{helper}(C)$가 merge vertex라면 대각선 $\mathrm{helper}(C)-u$를 추가합니다.
  - $C$를 $D$에서 삭제합니다.
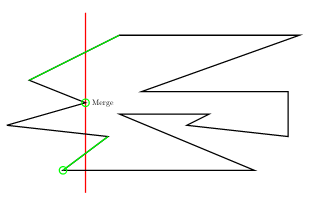
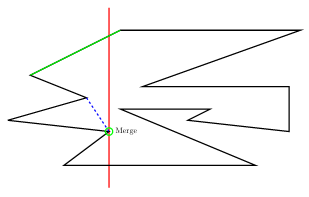
4. Merge Vertex
  - $u$를 포함하는 두개의 component $U, L$을 $D$에서 찾습니다. 여기서, $U$는 $L$보다 위쪽에 위치합니다.
  - $\mathrm{helper}(U)$가 merge vertex라면 대각선 $u-\mathrm{helper}(U)$를 추가합니다.
  - $\mathrm{helper}(L)$가 merge vertex라면 대각선 $u-\mathrm{helper}(L)$를 추가합니다.
  - $U$와 $L$을 $D$에서 삭제하고, 둘을 합친 component $C$를 $D$에 삽입합니다.
  - $\mathrm{helper}(C)$를 $u$로 놓습니다.
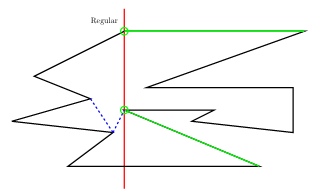
5. Regular Vertex
  - $u$를 포함하는 component $C$를 찾습니다.
  - $\mathrm{helper}(C)$가 merge vertex라면 대각선 $\mathrm{helper}(C)-u$를 추가합니다.
  - $\mathrm{helper}(C)$를 $u$로 놓습니다.

Example

다음 예에서 붉은색 선분은 sweepline, 초록색 선분은 각 monotone component와 sweepline의 위쪽 교차선분, 초록색 원은 각 monotone component의 helper입니다.

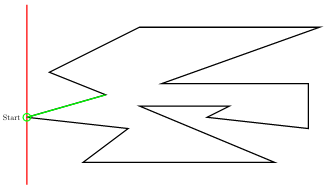
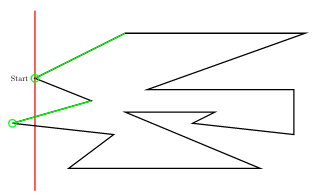
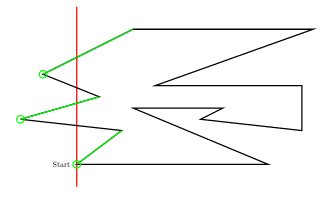
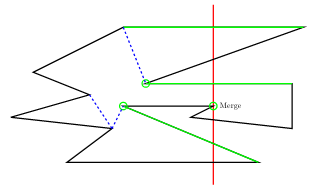
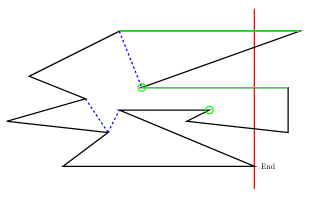
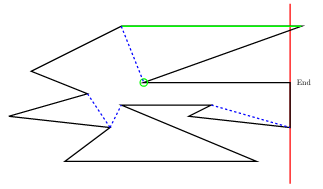
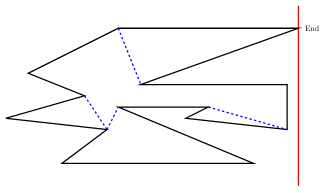
Implementation

다음은 정수 좌표를 가정한 implementation입니다. Type $T$는 maximum coordinate의 세제곱을 저장할 수 있어야 합니다.

template<class T>
struct point{
	T x{}, y{};
	point(){ }
	template<class U> point(const point<U> &otr): x(otr.x), y(otr.y){ }
	template<class U, class V> point(U x, V y): x(x), y(y){ }
	template<class U> explicit operator point<U>() const{ return point<U>(static_cast<U>(x), static_cast<U>(y)); }
	T operator*(const point &otr) const{ return x * otr.x + y * otr.y; }
	T operator^(const point &otr) const{ return x * otr.y - y * otr.x; }
	point operator+(const point &otr) const{ return {x + otr.x, y + otr.y}; }
	point &operator+=(const point &otr){ return *this = *this + otr; }
	point operator-(const point &otr) const{ return {x - otr.x, y - otr.y}; }
	point &operator-=(const point &otr){ return *this = *this - otr; }
	point operator-() const{ return {-x, -y}; }
#define scalarop_l(op) friend point operator op(const T &c, const point &p){ return {c op p.x, c op p.y}; }
	scalarop_l(+) scalarop_l(-) scalarop_l(*) scalarop_l(/)
#define scalarop_r(op) point operator op(const T &c) const{ return {x op c, y op c}; }
	scalarop_r(+) scalarop_r(-) scalarop_r(*) scalarop_r(/)
#define scalarapply(op) point &operator op(const T &c){ return *this = *this op c; }
	scalarapply(+=) scalarapply(-=) scalarapply(*=) scalarapply(/=)
#define compareop(op) bool operator op(const point &otr) const{ return tie(x, y) op tie(otr.x, otr.y); }
	compareop(>) compareop(<) compareop(>=) compareop(<=) compareop(==) compareop(!=)
#undef scalarop_l
#undef scalarop_r
#undef scalarapply
#undef compareop
	double norm() const{ return sqrt(x * x + y * y); }
	T squared_norm() const{ return x * x + y * y; }
	double angle() const{ return atan2(y, x); } // [-pi, pi]
	point<double> unit() const{ return point<double>(x, y) / norm(); }
	point perp() const{ return {-y, x}; }
	point<double> normal() const{ return perp().unit(); }
	point<double> rotate(const double &theta) const{ return point<double>(x * cos(theta) - y * sin(theta), x * sin(theta) + y * cos(theta)); }
	point reflect_x() const{ return {x, -y}; }
	point reflect_y() const{ return {-x, y}; }
	point reflect(const point &o) const{ return {2 * o.x - x, 2 * o.y - y}; }
	bool operator||(const point &otr) const{ return !(*this ^ otr); }
};
template<class T> istream &operator>>(istream &in, point<T> &p){ return in >> p.x >> p.y; }
template<class T> ostream &operator<<(ostream &out, const point<T> &p){ return out << "{" << p.x << ", " << p.y << "}"; }
template<class T>
double distance(const point<T> &p, const point<T> &q){
	return (p - q).norm();
}
template<class T>
T squared_distance(const point<T> &p, const point<T> &q){
	return (p - q).squared_norm();
}
template<class T, class U, class V>
T doubled_signed_area(const point<T> &p, const point<U> &q, const point<V> &r){
	return q - p ^ r - p;
}
template<class T>
T doubled_signed_area(const vector<point<T>> &a){
	assert(!a.empty());
	int n = (int)a.size();
	T res = a.back() ^ a.front();
	for(auto i = 1; i < n; ++ i) res += a[i - 1] ^ a[i];
	return res;
}
template<class T>
double angle(const point<T> &p, const point<T> &q){
	return atan2(p ^ q, p * q);
}
template<class T>
bool is_sorted(const point<T> &origin, point<T> p, point<T> q, point<T> r){
	p -= origin, q -= origin, r -= origin;
	T x = p ^ r, y = p ^ q, z = q ^ r;
	return x >= 0 && y >= 0 && z >= 0 || x < 0 && (y >= 0 || z >= 0);
} // check if p->q->r is sorted with respect to the origin
template<class T, class IT>
bool is_sorted(const point<T> &origin, IT begin, IT end){
	for(auto i = 0; i < (int)(end - begin) - 2; ++ i) if(!is_sorted(origin, *(begin + i), *(begin + i + 1), *(begin + i + 2))) return false;
	return true;
} // check if begin->end is sorted with respect to the origin

using pointint = point<int>;
using pointll = point<long long>;
using pointlll = point<__int128_t>;
using pointd = point<double>;
using pointld = point<long double>;

template<class T>
void triangulate(const vector<point<T>> &a, auto process_triangle){
	int n = (int)a.size();
	vector<int> order(n);
	iota(order.begin(), order.end(), 0);
	sort(order.begin(), order.end(), [&](int i, int j){ return a[i] < a[j]; });
	point<T> sweep;
	struct key_type{ // stores the line p-q
		mutable point<T> p, q;
	};
	auto cmp = [&](const key_type &a, const key_type &b)->bool{
		auto ya = a.p.x == a.q.x ? array{max(a.p.y, a.q.y), T(1)} : array{a.p.y * (a.q.x - sweep.x) + a.q.y * (sweep.x - a.p.x), a.q.x - a.p.x};
		auto yb = b.p.x == b.q.x ? array{min(b.p.y, b.q.y), T(1)} : array{b.p.y * (b.q.x - sweep.x) + b.q.y * (sweep.x - b.p.x), b.q.x - b.p.x};
		if(ya[1] < 0) ya = {-ya[0], -ya[1]};
		if(yb[1] < 0) yb = {-yb[0], -yb[1]};
		return ya[0] * yb[1] < yb[0] * ya[1];
	};
	struct mapped_type{
		array<int, 2> endpoint, helper;
	};
	map<key_type, mapped_type, decltype(cmp)> events(cmp);
	vector<array<int, 2>> roots;
	vector<int> id, next;
	auto new_node = [&](int i)->int{
		id.push_back(i), next.push_back(-1);
		return (int)id.size() - 1;
	};
	// partition polygon into monotone polygons
	for(auto i: order){
		sweep = a[i];
		int pi = (i + n - 1) % n, ni = (i + 1) % n;
		if(a[i] < a[pi] && a[i] < a[ni]){
			if(doubled_signed_area(a[pi], a[i], a[ni]) > 0){ // Start
				int u = new_node(i), v = new_node(i);
				events.insert({ {a[i], a[pi]}, { {u, v}, {u, -1} } });
				roots.insert(roots.end(), {u, v});
			}
			else{ // Split
				auto it = events.lower_bound({a[i], a[i]});
				int u = new_node(i), v = new_node(i);
				if(~it->second.helper[0] && ~it->second.helper[1]){
					next[it->second.helper[0]] = u;
					next[it->second.helper[1]] = v;
					events.insert({ {a[i], a[pi]}, { {it->second.endpoint[0], u}, {-1, u} } });
					it->second = { {v, it->second.endpoint[1]}, {v, -1} };
				}
				else if(~it->second.helper[0]){
					int j = it->second.helper[0];
					int w1 = new_node(id[j]);
					int w2 = new_node(id[j]);
					roots.push_back({w1, w2});
					next[w2] = u;
					next[it->second.endpoint[0]] = v;
					events.insert(it, { {a[i], a[pi]}, { {w1, u}, {-1, u} } });
					it->second = { {v, it->second.endpoint[1]}, {v, -1} };
				}
				else{
					int j = it->second.helper[1];
					int w1 = new_node(id[j]);
					int w2 = new_node(id[j]);
					roots.push_back({w1, w2});
					next[w1] = v;
					next[it->second.endpoint[1]] = u;
					events.insert(it, { {a[i], a[pi]}, { {it->second.endpoint[0], u}, {-1, u} } });
					it->first.p = a[id[j]], it->first.q = a[(id[j] + n - 1) % n];
					it->second = { {v, w2}, {v, -1} };
				}
			}
		}
		else if(a[i] > a[pi] && a[i] > a[ni]){ 
			if(doubled_signed_area(a[pi], a[i], a[ni]) > 0){ // End
				auto it = events.lower_bound({a[i], a[i]});
				int u = new_node(i);
				for(auto v: it->second.endpoint) next[v] = u;
				for(auto v: it->second.helper) if(~v) next[v] = u;
				events.erase(it);
			}
			else{ // Merge
				auto l = events.lower_bound({a[i], a[i]}), r = std::next(l);
				int u = new_node(i), v = new_node(i);
				if(~l->second.helper[0] && ~l->second.helper[1]){
					int w = new_node(i);
					next[l->second.helper[0]] = u;
					next[l->second.helper[1]] = w;
					next[l->second.endpoint[1]] = w;
				}
				else next[l->second.endpoint[1]] = u;
				if(~r->second.helper[0] && ~r->second.helper[1]){
					int w = new_node(i);
					next[r->second.endpoint[0]] = w;
					next[r->second.helper[0]] = w;
					next[r->second.helper[1]] = v;
				}
				else next[r->second.endpoint[0]] = v;
				r->second = { {l->second.endpoint[0], r->second.endpoint[1]}, {u, v} };
				events.erase(l);
			}
		}
		else{ // Regular
			auto it = events.lower_bound({a[i], a[i]});
			int u = new_node(i);
			if(a[pi] < a[i]){ // Left
				if(~it->second.helper[0] && ~it->second.helper[1]){
					int v = new_node(i);
					next[it->second.endpoint[0]] = v;
					next[it->second.helper[0]] = v;
					next[it->second.helper[1]] = u;
				}
				else{
					next[it->second.endpoint[0]] = u;
				}
				it->second = { {u, it->second.endpoint[1]}, {u, -1} };
			}
			else{ // Right
				if(~it->second.helper[0] && ~it->second.helper[1]){
					int v = new_node(i);
					next[it->second.helper[0]] = u;
					next[it->second.helper[1]] = v;
					next[it->second.endpoint[1]] = v;
				}
				else{
					next[it->second.endpoint[1]] = u;
				}
				it->first.p = a[i], it->first.q = a[pi];
				it->second = { {it->second.endpoint[0], u}, {-1, u} };
			}
		}
	}
	// triangulate each monotone polygons
	for(auto [p, q]: roots){
		bool stack_type;
		vector<int> stack{id[p]};
		auto push = [&](bool side, int i)->void{
			if((int)stack.size() == 1){
				stack.push_back(i);
				stack_type = side;
				return;
			}
			int last = stack.back(), j = last;
			stack.pop_back();
			while(!stack.empty() && doubled_signed_area(a[stack.back()], a[stack_type ? i : j], a[stack_type ? j : i]) > 0){
				process_triangle(stack.back(), stack_type ? i : j, stack_type ? j : i);
				j = stack.back();
				stack.pop_back();
			}
			stack.insert(stack.end(), {side == stack_type ? j : last, i});
			stack_type = side;
		};
		p = next[p], q = next[q];
		while(p != q){
			bool side;
			int i;
			if(a[id[p]] < a[id[q]]) side = false, i = id[p], p = next[p];
			else side = true, i = id[q], q = next[q];
			push(side, i);
		}
		push(!stack_type, id[p]);
	}
}

Fast Polygon Triangulation

Table Of Contents

Introduction

Preliminaries

Degeneracy

Strict Total Order

Monotone Polygon

Montone Polygon Triangulation

Example

Polygon Triangulation

Boundary Vertex Classification

Sweepline Events

Example

Implementation

Fully Dynamic Min Cut

람다 표현과 처치 인코딩(1)