June 21, 2021 06:00

평면 연결 그래프에서 $V$와 $E$를 각각 정점과 간선의 집합 $f$를 면의 개수라고 할 때, $|V|-|E|+f=2$라는 공식이 성립하고 우리는 흔히 이를 오일러 지표라고 부릅니다.

여기서 면은 outer face, 즉, 무한히 바깥으로 뻗어나가는 면을 포함합니다.

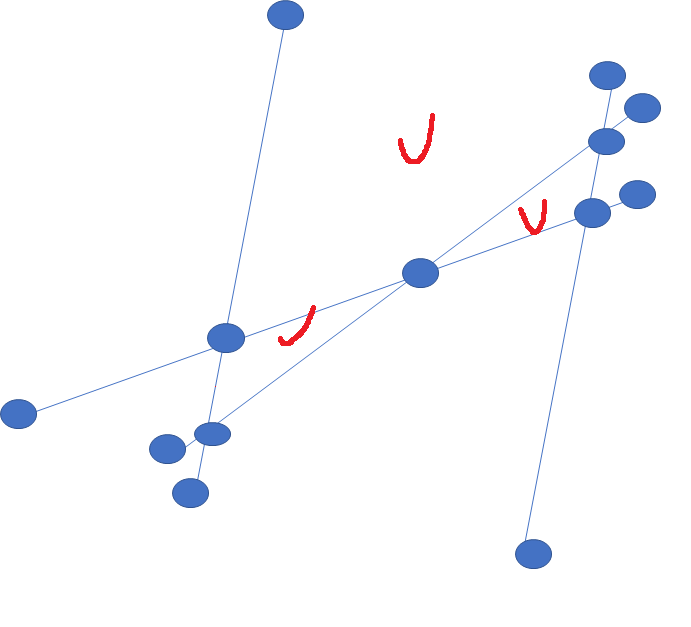
위의 그래프에서도 이 식이 성립함을 관찰하실 수 있습니다. 평면 연결 그래프 $G$에서 $|V|-|E|+f=2$라는 사실을 귀납법을 이용하여 증명해봅시다. 우선 임의의 트리는 항상 $|V|-|E|=1$ 이므로, 이 공식이 성립함을 쉽게 보일 수 있습니다.

만약 그래프가 트리가 아닌 경우, 임의의 사이클이 존재하고. 사이클을 구성하는 임의의 간선은 항상 서로 다른 두 면에 붙어 있습니다. 그런 간선 중 하나를 지워서 만든 그래프를 $G’$이라고 합시다. $G’$은 여전히 평면 연결 그래프이고, 따라서 귀납법에 의해 $|V|-|E|+f=2$입니다. $G’$에서 아까 지웠던 그 간선을 추가하면, 간선 개수와 면의 개수가 각각 하나씩 증가하게 되므로 역시 $|V|-|E|+f=2$ 이 되므로, 이것으로 증명을 완료하였습니다.

흥미로운 점은, 구(sphere) 위에 그려진 그래프도 하나의 평면 그래프처럼 생각할 수 있어서, 마찬가지로 다면체에서도 이 공식이 성립함을 보일 수 있습니다. 예를 들어, 정육면체는 $|V|=8, |E|=12, f=6$입니다.

그러면, 오일러 지표가 문제에서 어떻게 쓰이는지 한번 알아보겠습니다.

Hoarse Horses(링크)

$N$개의 선분이 주어졌을 때, 선분으로 둘러싸이는 면의 개수를 구하는 문제입니다. 즉, 기존의 면 개념에서 outer face를 제외한 것의 개수입니다.

이 문제에서 면의 개수를 구하는 건 쉽지 않아 보입니다. 대신, 우리는 점의 개수와 선의 개수를 보다 쉽게 알 수 있고, 이를 이용해서, 오일러 지표를 통해 면의 개수 $f$를 구할 수 있을 것으로 기대됩니다.

그래프에서 선분을 하나의 간선으로, 양 끝을 두 개의 정점으로 생각해 봅시다. 평면 그래프의 정의에 의해, 아래와 같이 서로 교차하는 간선이 존재해선 안됩니다.

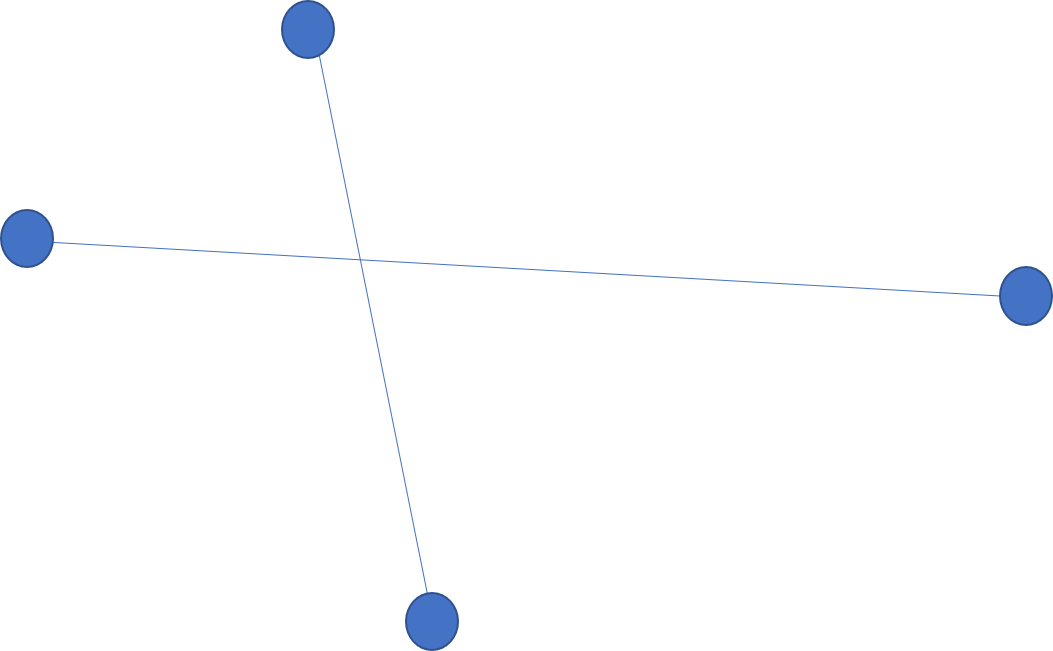
하지만, 이 경우는 아래처럼 교차점도 하나의 정점으로 생각할 수 있고. 이 경우 평면 그래프가 성립하는 것을 확인할 수 있습니다.

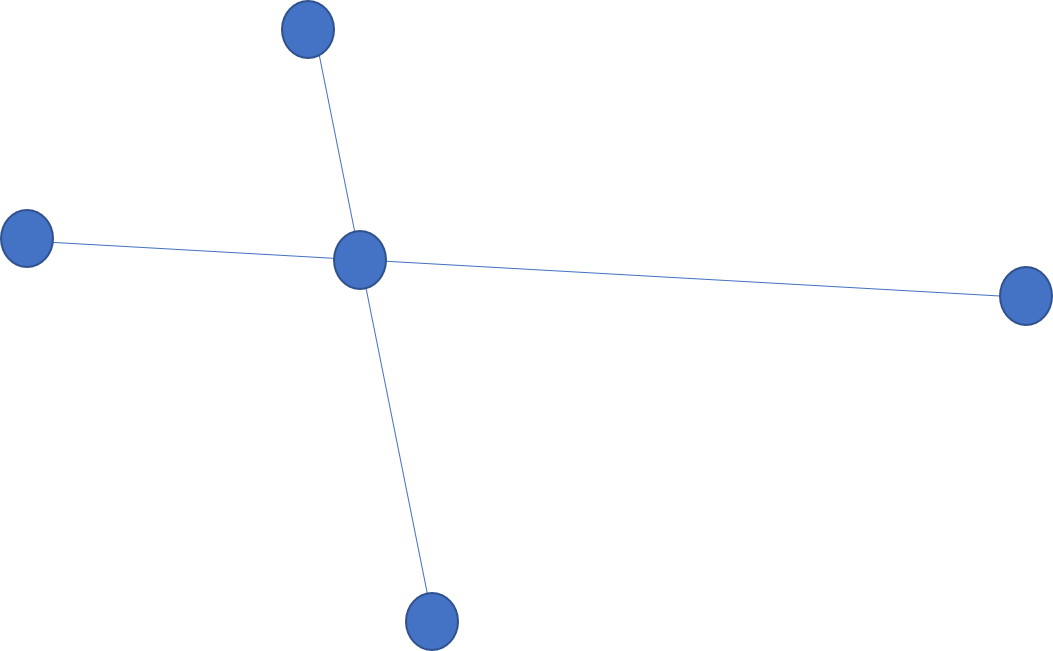
아래처럼, 주어진 평면 그래프가 연결 그래프가 아닌 경우에는 $|V|-|E|+f=2$ 가 성립하지 않는 것을 볼 수 있는데, 이 경우에는 어떻게 해야 할까요?

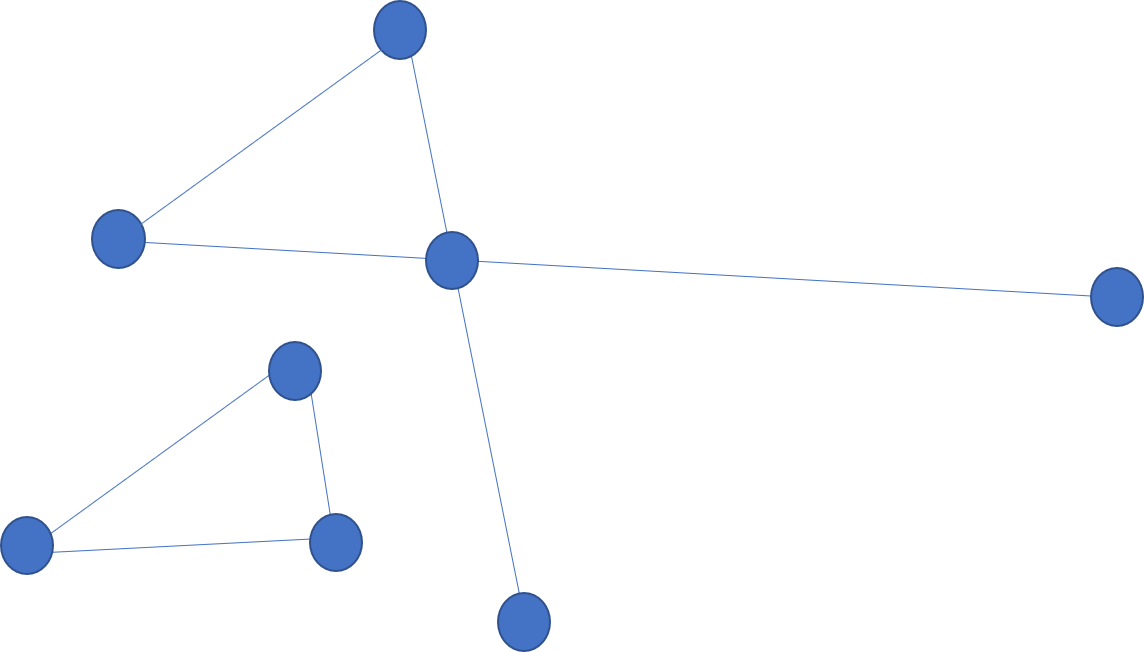
기존의 평면 연결 그래프에서 outer face를 제외한 면의 수 $f’$을 세면, $|V|-|E|+f’=1$이 되고, 따라서 하나의 컴포넌트에 대해서, $|V|-|E|+f’=1$이라고 생각할 수 있습니다. 따라서, $C$를 컴포넌트의 개수라고 할 때, 임의의 평면 그래프에서 선으로 둘러싸인 면의 개수$f’$에 대해 $|V|-|E|+f’=C$가 됩니다. 즉, $f’=C-|V|+|E|$입니다.

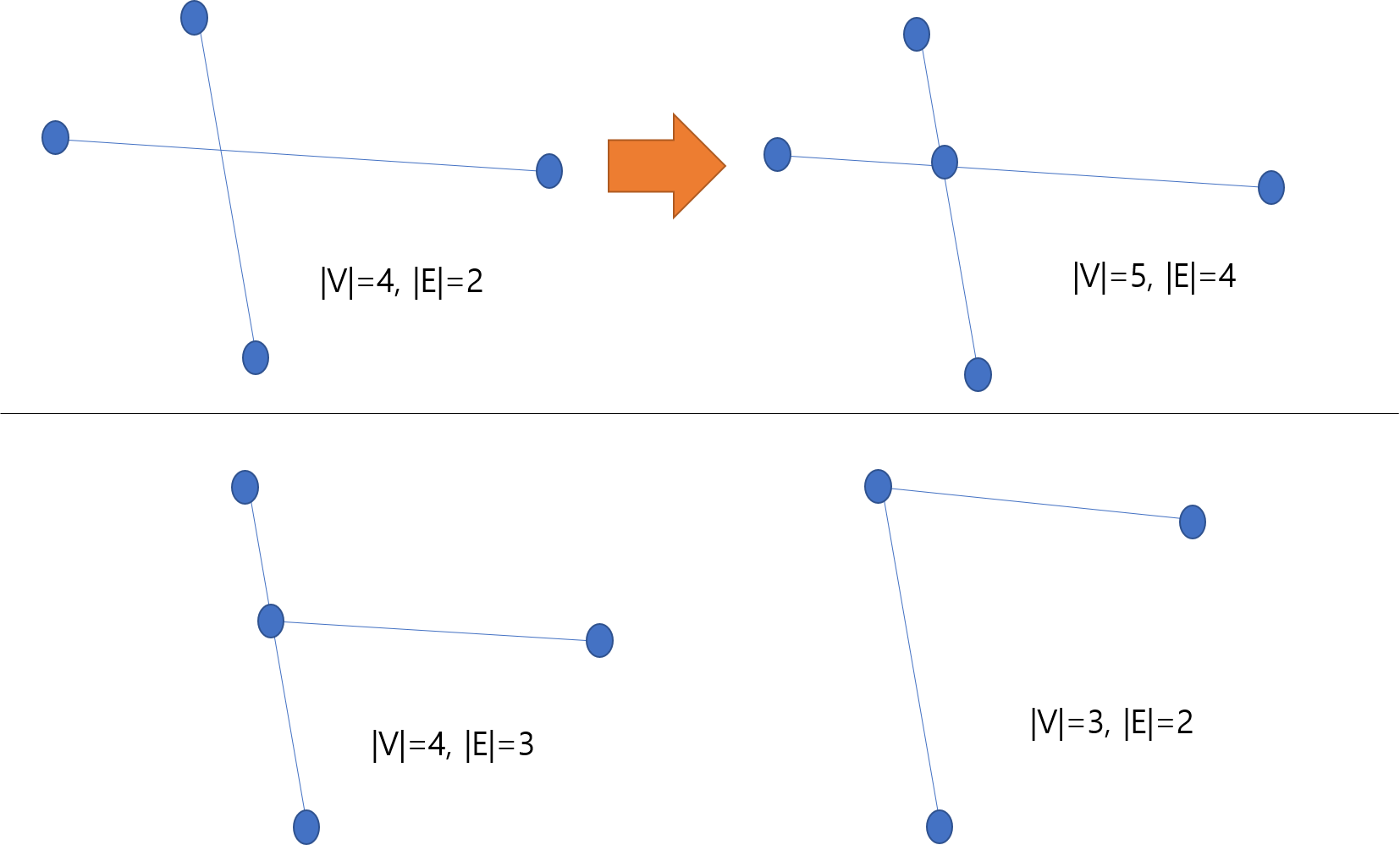
어떤 두 선분 $|V|=4, |E|=2 (|V|-|E|=2)$에 대해, 선분이 교차할 때. 교차점을 하나의 정점으로 취급하여, 그래프를 평면 그래프로 바꾸는 과정에서 점과 선의 개수 변화를 살펴보면. $|V|-|E|$가 $1$만큼 증가하는 것을 관찰할 수 있습니다.

즉, 어떤 두 선분이 교차할 때마다 $f’$가 1씩 증가합니다. 따라서, 문제에서 구하고자 하는 면의 개수 $f’$는 $교차하는\space선분\space쌍의\space수 - (2N - N) + C$가 됩니다.

이를 구현한 코드입니다. 선분 교차 판정은 벡터의 외적, 컴포넌트 관리는 Union-Find 자료구조를 이용하였습니다.

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;

int p[1000];
int find(int a) {
    if (p[a] == -1) return a;
    return p[a] = find(p[a]);
}

void merge(int a, int b) {
    a = find(a); b = find(b);
    if (a == b) return;
    p[b] = a;
}

struct line {
    pii a, b;
} vec[1000];

pii operator- (pii a, pii b) {return pii(a.first-b.first, a.second-b.second);}
ll operator/ (pii a, pii b) {return (ll)a.first*b.second - (ll)a.second*b.first;}
ll ccw(pii a, pii b, pii c) {
    ll ret = (b-a) / (c-a);
    if (ret < 0) return -1;
    if (ret == 0) return 0;
    return 1;
}

int isInter(line a, line b) {
    ll aa = ccw(a.a, a.b, b.a);
    ll bb = ccw(a.a, a.b, b.b);
    ll cc = ccw(b.a, b.b, a.a);
    ll dd = ccw(b.a, b.b, a.b);

    if (aa*bb>0 || cc*dd>0) return 0;
    if (aa*bb == 0 && cc * dd == 0) {
        if (a.a > a.b) swap(a.a, a.b);
        if (b.a > b.b) swap(b.a, b.b);
        if (a.b < b.a || b.b < a.a) return 0;
    }

    return 1;
}

int main() {
    memset(p, -1, sizeof(p));

    int n;
    scanf("%d", &n);

    int ans = 0;
    line t;
    for (int i = 0; i < n; i++) {
        scanf("%d %d %d %d", &t.a.first, &t.a.second, &t.b.first, &t.b.second);
        vec[i] = t;

        for (int j = 0; j < i; j++) {
            int tmp = isInter(vec[i], vec[j]);
            if (tmp) {
                ans++;
                if (find(i) != find(j)) {
                    merge(i, j);
                    ans--;
                }
            }
        }
    }

    printf("%d", ans);
}

// author: rdd6584

오일러 지표를 이용하여 풀 수 있는 문제들입니다.

달고나(링크)

Hoarse Horses와 비슷한 문제이지만, 원도 등장합니다. 원에 대한 처리만 다를 뿐 문제 풀이는 거의 동일합니다.

삼분 그래프(링크)

어떤 쿼리에 대해, 컴포넌트의 개수를 구하는 문제이니. 점, 선, 면의 개수의 변화량을 구하면 컴포넌트의 변화량도 구할 수 있습니다.

선의 변화량은 직선 $A$를 지나는 간선 개수 $+$ $B$를 지나는 간선 개수이고, 점의 변화량은 선의 변화량의 $2$배입니다. 면의 변화량은 $A$를 지나거나 $B$를 지나는 면의 개수만큼 감소하게 됩니다.

데이터 제작(링크)

오일러 지표에 의해, $N-M+K=C$입니다. 평면 그래프에서 $M \leq 3N - 6$이 성립합니다. 따라서, $N$개의 정점에 대해 $3N - 6$개의 간선을 좌표 범위 내에 전부 표현할 수 있다면, 그 이하의 간선을 가지는 평면 그래프도 마찬가지로 찾을 수 있게 됩니다.

읽어주셔서 감사합니다.