cheetose's profile image

cheetose

July 19, 2021 00:00

서론

지난 글에서 아주 기본적인 (noise가 없는) Binary modulation / demodulation에 대해서 알아보고, 현재 통신 시스템에서 가장 쉽게 볼 수 있는 AWGN 채널에 대해서 간략하게 알아보았습니다.

이번 글에서는 지난 글에서 짧게 언급한 AWGN 채널에 대해 좀 더 자세히 다룰 예정입니다. 또한 AWGN 채널에서의 Binary modulation / demodulation에 대해서 데이터가 잘못 전송될 확률을 구하고, 기존 Binary에서 이를 M개의 bit로 확장시킨 M-ary modulation / demodulation에 대해서 알아보도록 하겠습니다.

본론

AWGN 채널

지난 글에서 작성한 내용을 잠깐 언급하고 가자면, AWGN은 Additive White Gaussian Noise 의 약자로, 어떤 메시지를 송신했을 때 수신단에서 받는 메시지는 해당 메시지에 단순히 Gaussian random variable이 더해진 값을 받게됩니다.

이를 binary antipodal에 적용해보면, 우리가 어떤 메시지 $s_m(t)$를 보낼 때 수신단에서 받는 메시지는 $r(t) = s_m(t) + n(t) = s_m\psi(t) + n(t)$입니다. 이를 demodulation하기 위해서 noiseless 채널에서와 마찬가지로 $\psi(t)$를 곱한 뒤에 해당 구간에 대해서 적분을 해주면 됩니다. 이를 도식화 하면 아래 그림처럼 표현할 수 있습니다.

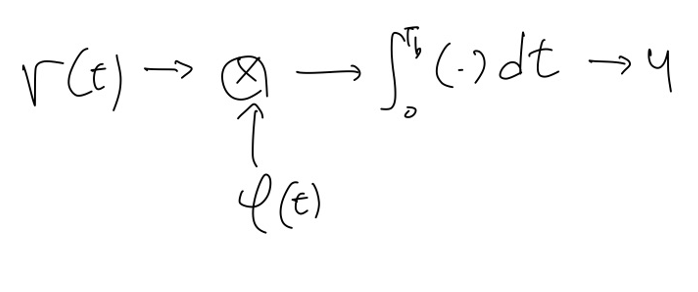
이 과정을 수식으로 좀 더 자세히 써보겠습니다.

$y = \int_{0}^{T_b}{r(t)\psi(t)dt}$

$= \int_{0}^{T_b}{(s_m\psi(t) + n(t))\psi(t)dt}$

$= \int_{0}^{T_b}{s_m\psi^2(t)dt} + \int_{0}^{T_b}{n(t)\psi(t)dt}$

$= s_m\int_{0}^{T_b}{\psi^2(t)dt} + \int_{0}^{T_b}{n(t)\psi(t)dt}$

여기서 $\int_{0}^{T_b}{\psi^2(t)dt} = 1$ 이므로 첫 번째 항은 $s_m$이 됩니다. 두 번째 항을 $n$으로 표현하면 최종적으로 아래와 같이 간단하게 됩니다.

$y = s_m + n$

여기서 $n(t)$는 random process이고, $n$은 random variable이라는 차이점이 있습니다. 여기서 나온 $n$은 평균이 0이고 분산이 $\sigma_n^2$인 RV입니다. 이제 정확한 $\sigma_n^2$의 값을 구해봅시다.

$\sigma_n^2 = E[n^2] - (E[n])^2$인데 $E[n] = 0$이므로 $\sigma_n^2 = E[n^2]$입니다. 고로 본격적으로 $E[n^2]$를 구해보겠습니다. 해당 식에 $n=\int_{0}^{T_b}{n(t)\psi(t)dt}$를 대입하여 전개하겠습니다.

$E[n^2] = E[\int_{0}^{T_b}{n(t_1)\psi(t_1)dt_1}\int_{0}^{T_b}{n(t_2)\psi(t_2)dt_2}]$

$= E[\int_{0}^{T_b}{\int_{0}^{T_b}{n(t_1)n(t_2)\psi(t_1)\psi(t_2)dt_1}dt_2}]$

$= \int_{0}^{T_b}{\int_{0}^{T_b}{E[n(t_1)n(t_2)\psi(t_1)\psi(t_2)]dt_1}dt_2}$

$= \int_{0}^{T_b}{\int_{0}^{T_b}{E[n(t_1)n(t_2)]\psi(t_1)\psi(t_2)dt_1}dt_2}$

$n(t)$의 correlation은 $R_n(\tau)=\frac{N_0}{2} \delta(\tau)$이라고 지난 글에서 설명했습니다. 따라서 $E[n(t_1)n(t_2)] = R_n(t_1 - t_2) = \frac{N_0}{2} \delta(t_1 - t_2)$가 됩니다. 따라서

$E[n^2] = \frac{N_0}{2} \int_{0}^{T_b}{\int_{0}^{T_b}{\delta(t_1 - t_2)\psi(t_1)dt_1}\psi(t_2)dt_2}$

$= \frac{N_0}{2} \int_{0}^{T_b}{\int_{0}^{T_b}{\delta(t_1 - t_2)\psi(t_2)dt_1}\psi(t_2)dt_2}$

$= \frac{N_0}{2} \int_{0}^{T_b}{\psi^2(t_2)dt_2} = \frac{N_0}{2}$

즉, $n$의 분산은 $\frac{N_0}{2}$임을 알 수 있습니다. 이를 한 마디로 정리하자면 “y는 평균이 $s_m$이고 분산이 $\frac{N_0}{2}$인 Gaussian RV를 따른다”고 할 수 있습니다.

하지만 이 y값이 우리가 송신한 신호인 x와 정확히 일치하지 않기 때문에 y를 보고 송신 신호를 “추측”해야합니다. 우리는 이 추측을 할 때, 수신 메시지가 y일 때, 송신 메시지가 $m_i$일 확률이 가장 큰 $i$를 선택하게 될 것입니다. 이를 MAP detection이라 하고 수식으로는 $P_{x \vert y}(i \vert y)$와 같이 씁니다.

해당 식은 베이즈 정리에 의해 $\frac{P_{y \vert x}(y \vert i)P_x(i)}{P_y(y)}$로 변형이 가능하고, 이 때 분모에 해당하는 값은 상수이므로 $P_{y \vert x}(y \vert i)P_x(i)$가 최대가 되는 $m_i$를 선택하면 됩니다. 여기서 $y=x+n$임을 이용하여 $P_{y \vert x}(y \vert i)$을 간단히 바꿔보겠습니다.

$P_{y \vert x}(y \vert i) = \frac{P(y=y, x=x_i)}{x=x_i}$

$= \frac{P(n=y-x_i, x=x_i)}{P(x=x_i)}$

$= \frac{P(n=y-x_i)P(x=x_i)}{P(x=x_i)} (\because x,n$ 은 서로 독립적$)$

$=P_n(y-x_i)$

n의 PDF는 평균이 0이고 분산이 $\frac{N_0}{2}$인 Gaussian RV를 따르므로 $P_n(u) = (\pi N_0)^{\frac{N}{2}exp(-\frac{\vert u \vert^2}{N_0})}$ 입니다. 여기서 $N$은 constellation의 차원을 의미합니다.

이제 $P_n(y-x_i)P_x(i)$ 를 최대화 하는 $i$를 고르는 것이 목표입니다. 이는 $exp(-\frac{\vert y-x_i \vert^2}{N_0})P_x(i)$ 또는 $-\frac{\vert y-x_i \vert^2}{N_0}+ln P_x(i)$를 최대화 하는 $i$를 고르는 것과 동치이고, 결과적으로 $\vert y-x_i \vert^2 - N_0 ln P_x(i)$를 최소화하는 문제로 바뀝니다.

어떤 신호 x를 송신할 확률이 uniform distribution을 따른다고 가정하면 (실제로도 거의 그렇습니다.) $P_x(i)$ 역시 상수로 취급할 수 있기때문에 결과적으로 $P_{y \vert x}(y \vert i)$값이 가장 큰 $m_i$를 선택하는 ML detection 문제로 바뀝니다. MAP detection에서 했던 것과 같은 방식으로 우리는 이를 $\vert y-x_i \vert^2$를 최소화하는 문제로 바꿀 수 있습니다. 즉, constellation 상에서 유클리드 거리가 가장 가까운 점을 선택하면 된다는 뜻입니다.

예를 들어 constellation과 수신된 $y$가 아래 그림과 같이 이루어져있다고 가정해봅시다.

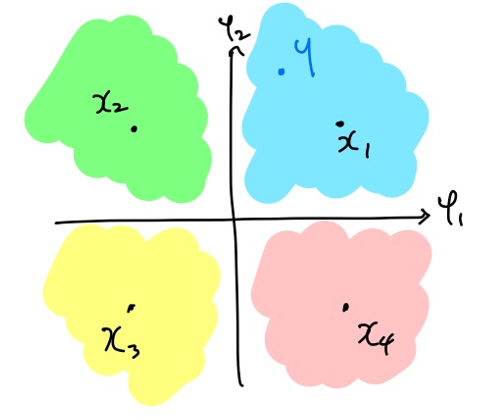
그러면 우리는 $y$와 가장 가까운 $x_1$을 송신한 신호라고 추측할 수 있습니다. 위와 같은 경우에는 $y$가 속해있는 사분면에 해당하는 점에서 송신한 것으로 추측하면 될 것입니다.

Probability of error

Binary antipodal의 경우를 예로 들어 에러가 발생할 확률을 구하는 방법을 알아보겠습니다.

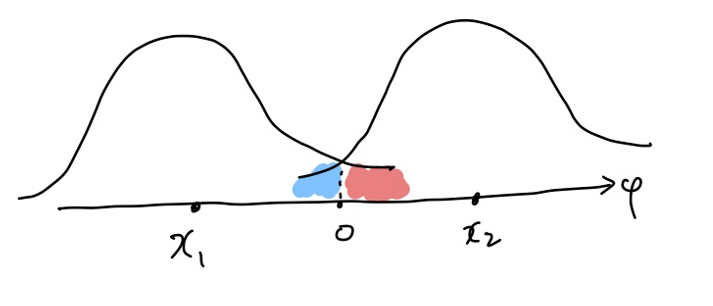
Binary antipodal은 constellation이 위 그림과 같은 형태를 띕니다. 여기서 에러가 발생하기 위해서는 $x_1$을 송신했는데 빨간색 부분에 해당하는 값이 수신이 되거나, $x_2$를 송신했는데 파란색 부분에 해당하는 값이 수신되면 됩니다. 이를 수식으로 표현하면 $P(e) = P(y>0 \vert x=x_1)P(x=x_1) + P(y<0 \vert x=x_2)P(x=x_2)$입니다. $P(x=x_1)=P(x=x_1)=\frac{1}{2}$이고, $P(y>0 \vert x=x_1)= P(y<0 \vert x=x_2)$이므로 $P(y>0 \vert x=x_1)$ 값을 구해주면 에러가 발생할 확률이 나옵니다. 해당 값은 빨간색 부분의 면적과 같기 때문에 적분을 통해 구할 수 있습니다.

$\int_{0}^{\infty}{\frac{1}{\sqrt{2 \pi \sigma^2}}exp(-\frac{(y+\sqrt{\epsilon_b})^2}{2 \sigma^2})dy}$ 을 구하면 해당 넓이를 구할 수 있고, 여기서 $y’ = \frac{y+\sqrt{\epsilon_b}}{\sigma}$ 로 치환하면

$\int_{\sqrt{\epsilon_b} / \sigma}^{\infty}{\frac{1}{\sqrt{2 \pi}}exp(-\frac{y’^2}{2 })dy’}$ 로 정리됩니다. 이 적분식을 직접 구할 수는 없기 때문에 Q 함수라는 새로운 함수를 도입해서 식을 표현해야 합니다. Q 함수는 $Q(x)=\frac{1}{\sqrt{2 \pi}}\int_{x}^{\infty}{exp(-\frac{u^2}{2 })du}$ 로 정의되는 함수로, 이를 이용하면 $P(e) = Q(\frac{\sqrt{\epsilon_b}}{\sigma})$ 임을 알 수 있습니다.

위의 내용은 Binary system에서 적용한 방식이지만, M-ary system에서도 같은 방식으로 구할 수 있습니다. (사실 $P(e)$를 계산할 때 $\sqrt{\epsilon_b}$를 이용하는 것보다 두 점 사이의 거리인 $d$ 또는 가장 가까운 두 점 사이의 거리인 $d_{min}$을 더 많이 사용합니다. $d$를 이용한 경우 $d=2\sqrt{\epsilon_b}$ 이므로 에러가 발생할 확률은 $Q(\frac{d}{2\sigma}))$ 가 됩니다.)

M-ary system

지금까지 설명했던 내용은 한 번에 전송하는 데이터의 비트 개수가 1인 Binary modulation / demodulation에 관련된 내용이었습니다. 하지만 이는 데이터 전송률이 그닥 좋지 않기때문에 한 번에 여러 개의 비트를 전송하는 방식을 택하게 됩니다. 그 중에 가장 대표적인 방식 2가지를 이번 글에서 설명하겠습니다. (본 글에서는 M=4인 경우를 예로 들어 설명하겠습니다.)

M-ary PAM

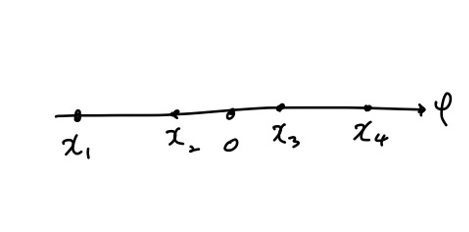
M-ary PAM 은 constellation이 위 그림과 같은 전송방식을 의미합니다. 위 예시에서는 M=4이므로 한 번에 보내는 신호의 비트의 개수가 2개입니다. (각 점이 00, 01, 10, 11에 대응합니다.) M-ary PAM의 에러 발생 확률을 구해보겠습니다.

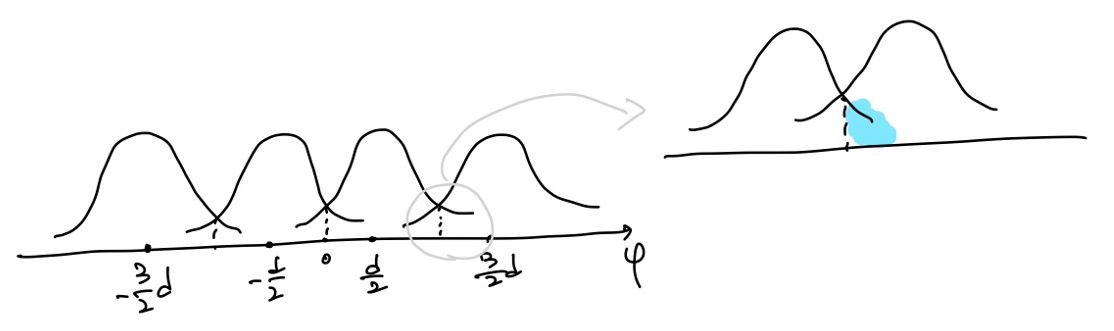
위 그림에서 보는 것처럼, 양 끝 점과 그 외의 점의 에러 발생 확률이 다릅니다. 양 끝 점은 송신 신호를 잘못 추측하는 경우가 1가지이지만, 나머지는 모두 2가지이기 때문입니다. 오른쪽 그림의 파란색 부분에 해당하는 넓이가 $Q(\frac{d}{2\sigma}))$임을 위에서 보였고, 이것이 총 6개 있기 때문에 에러가 발생할 확률은 $\frac{6}{4}Q(\frac{d}{2\sigma}))$입니다. 4로 나눈 이유는 각 점이 송신될 확률이 $\frac{1}{4}$로 동일하기 때문입니다. 이를 M-ary PAM으로 확장한다면 에러가 발생할 확률은 $2\frac{M-1}{M}Q(\frac{d}{2\sigma}))$이 됩니다.

M-ary PSK

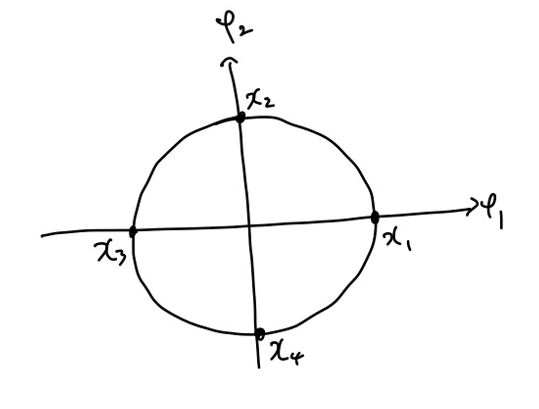
M-ary PSK는 위의 그림처럼 M개의 점이 원점을 중심으로 한 원의 둘레를 일정한 간격으로 놓여있는 형태입니다. M이 8 이상인 경우에는 정확한 에러 발생 확률을 구하기 매우 어렵기 때문에 M=4인 경우에 대해서 에러 발생 확률을 구해보겠습니다. (M=2인 경우는 Binary antipodal과 동일합니다.)

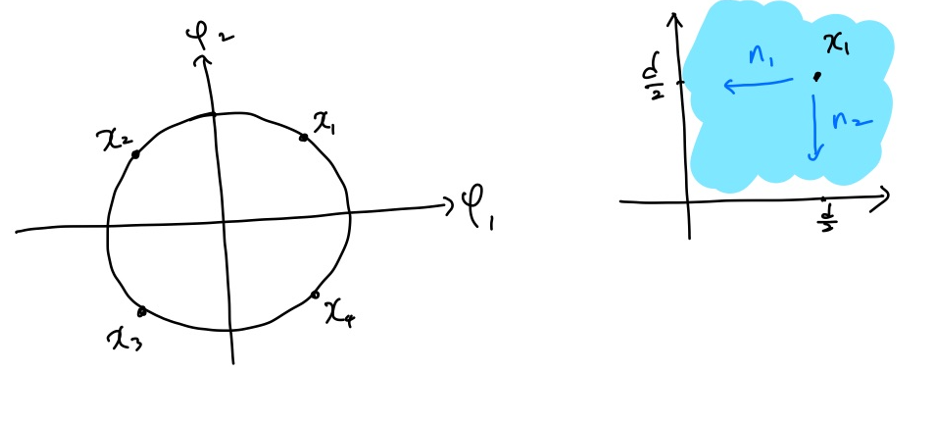
왼쪽 그림처럼 constellation을 회전시켜도 성능에는 변화가 없다는 사실을 이용하겠습니다. 그러면 오른쪽 그림에서의 $n_1$ 방향과 $n_2$ 방향의 노이즈를 확인해서 두 방향 모두 정확한 추측을 한 것이 아니라면 해당 신호는 에러가 난 것입니다. 따라서 1에서 에러가 나지 않을 확률을 빼주면 에러 발생 확률이 됩니다.

정확한 추측을 할 확률은 $P_c = P(n_1 < \frac{d}{2}, n_2 < \frac{d}{2})$입니다. $n_1, n_2$는 서로 독립적이므로 $P_c = P(n_1 < \frac{d}{2})P(n_2 < \frac{d}{2})$ 로 쓸 수 있고, $P(n_1 < \frac{d}{2})$과 $P(n_2 < \frac{d}{2})$는 $(1-Q(\frac{d}{2\sigma}))$로 같으므로 $P_c = (1-Q(\frac{d}{2\sigma}))^2$ 이 됩니다. 따라서 에러 발생 확률은 $P(e) = 1- (1-Q(\frac{d}{2\sigma}))^2 = 2Q(\frac{d}{2\sigma}) - Q^2(\frac{d}{2\sigma})$ 입니다.

대부분의 경우 Q 함수의 값이 $10^{-5}$ 이하이기 때문에 $P(e) \simeq 2Q(\frac{d}{2\sigma})$ 로 근사시켜서 계산합니다.

Union bound

하지만 모든 constellation에 대해 이런 식으로 정확하게 구할 수는 없기 때문에 에러 발생 확률의 상한을 계산하여 그 값으로 근사시켜 계산하는 방법을 주로 사용합니다. $d_{min}$을 constellation 상에서 가장 가까운 두 점 사이의 거리라고 했을 때, $P(e) \leq (M-1)Q(\frac{d_{min}}{2\sigma})$ 가 성립합니다. 증명은 다음과 같습니다.

$\epsilon_{ij}$를 $x_i$를 송신했는데 $x_j$라고 추측하는 사건이라고 정의하고, $d_{ij}=\vert x_i - x_j \vert$라 정의하겠습니다. 그러면 $x_i$를 송신했을 때 에러가 발생할 확률은 $P(e \vert i) = \sum_{j \neq i} P(\epsilon_{ij}) = (M-1)P(\epsilon_{ij})$ 입니다. 여기서 $P(\epsilon_{ij}) \leq P(\vert y - x_i \vert^2 \geq \vert y - x_j \vert^2) = Q(\frac{d_{ij}}{2\sigma})$ 이고, $d_{ij} \geq d_{min}$ 이므로 $P(e) \leq (M-1)Q(\frac{d_{min}}{2\sigma})$ 를 만족합니다.

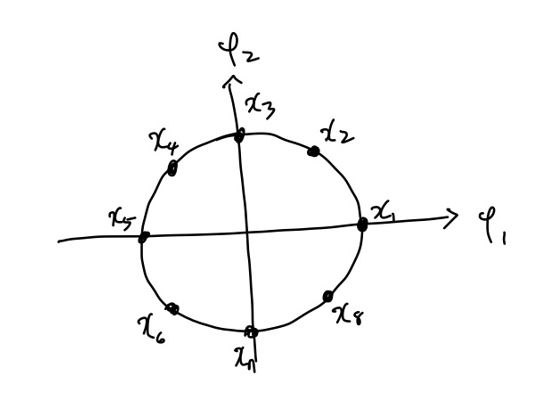
앞에서 8PSK의 에러 발생 확률을 정확히 구하기 매우 어렵다고 했지만, union bound를 이용하면 그 확률의 상한을 구할 수 있습니다.

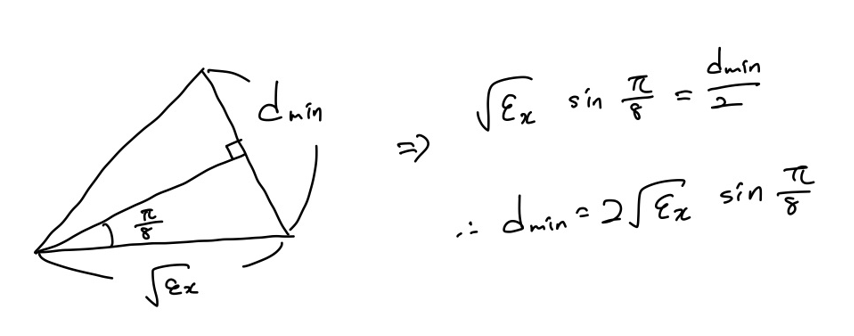
$d_{min}$은 위에서 구한대로 $2\sqrt{\epsilon_x}sin \frac{\pi}{8}$이므로 $P(e) \leq 7Q(\frac{\sqrt{\epsilon_x}}{\sigma}sin \frac{\pi}{8})$ 임을 알 수 있습니다.

Nearest Neighbor Union Bound (NNUB)

기존 union bound보다 더 엄밀한 상한을 제시하는 NNUB에 대해 설명하겠습니다. 우선 $N_i$를 $x_i$에서 거리가 $d_{min}$인 점의 개수라고 정의하겠습니다. 그리고 $N_i$의 평균을 $N_e = \sum_i N_i P(x=x_i)$라 하면 $P(e) \leq N_e Q(\frac{d_{min}}{2\sigma})$ 가 성립합니다. 증명은 다음과 같습니다.

$P(e) = P(e \vert i)P(x=x_i) \leq \sum_i N_i Q(\frac{d_{min}}{2\sigma})P(x=x_i) = N_e Q(\frac{d_{min}}{2\sigma})$

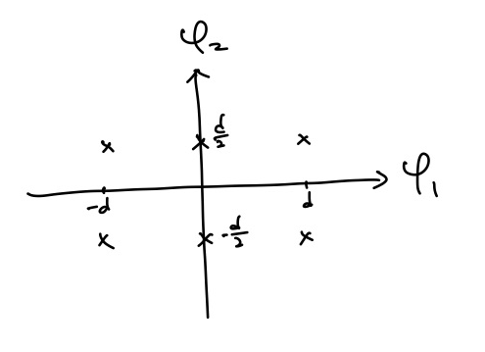
예제로 constellation이 위 그림과 같을 때의 NNUB를 구해보겠습니다. 4개의 점에 대해서 $N_i=2$ 를 만족하고, 2개의 점에 대해 $N_i=3$ 을 만족합니다. 따라서 $N_e = \frac{1}{6}(2 \times 4 + 3 \times 2) = \frac{7}{3}$ 이므로 $P(e) \leq \frac{7}{3} Q(\frac{d}{2\sigma})$ 를 만족합니다.

그냥 union bound를 통해 구하면 $P(e) \leq (M-1)Q(\frac{d}{2\sigma}) = 5Q(\frac{d}{2\sigma})$ 와 같은 상한을 구할 수 있는데, 이보다 더 엄밀한 상한을 제시하는 것을 볼 수 있습니다.

결론

본 글에서는 지난 글에 이어 AWGN채널, M-ary system, 그리고 에러 발생 확률을 구하는 방법과 대략적인 상한에 대해서 알아보았습니다.

다음 글에서는 현재 사용되고 있는 constellation인 QAM과 특정 주파수 사이의 신호만 통과시키는 passband system에 대해 작성하겠습니다.

Reference

• Fundamentals of Communication Systems, John G Proakis