알고리즘 문제 접근 과정 2
알고리즘 문제 접근 과정 2
이번 포스트에서도 ‘알고리즘 문제 접근 방법’에서 진행했듯이 특정 문제를 해결하기 위해 가장 낮은 단계의 접근에서부터 최종 해법까지 해결해나가는 과정을 작성합니다.
최대한 다양한 유형의 문제들을 다루어, 많은 문제 유형에서의 접근 방법에 대한 실마리를 드리는 역할을 하려 합니다.
나무 막대 - Taejon Asia Regional 2001 B번
관찰
우리는 문제를 이해할 때, 복잡하게 주어진 조건을 머리에 표상하기 쉬운 형태로 변경하는 것이 중요합니다.
주어진 조건에서, 한 번 기계를 작동할 때, 그 다음에 오는 막대의 길이와 무게가 모두 더 크거나 같다면 따로 시간을 들이지 않고 막대를 가공할 수 있습니다. 그리고 만약 그렇지 않다면 도구를 바꾸기 위한 1분의 준비시간이 필요하다고 되어있습니다.
하지만 이를 다르게 말한다면, 우리는 다른 도구를 사용하는 하나의 기계가 더 필요하다는 말이 되는 것이고, 우리는 위와 같은 일을 할 수 있는 기계의 수를 늘리는 것으로 준비 시간의 개념을 피할 수 있습니다.
즉, 우리는 위 문제를
- 첫 막대를 가공하고나면 그 이후에는 항상 길이와 무게 모두 더 크거나 같은 막대만 가공할 수 있는 기계를
- 최소로 사용하여 목재들을 모두 가공할 때, 필요한 기계의 수
의 형태로 생각할 수 있게 됩니다.
이제, 주어진 막대들도 좀 더 편하게 이해할 수 있도록 문제를 생각해봅시다. 우리가 문제를 해결할 때 큰 걸림돌이 되는 부분은, 바로 현재 가공한 막대 뒤에 어떤 막대를 가공할 것인지입니다.
주어진 예시처럼 (4,9), (5,2), (2,1), (3,5), (1,4)의 막대가 존재한다면, (2, 1) 막대 뒤에 바로 (5, 2)를 사용하는 방법도 있지만, (3, 5)를 사용하는 방법도 있을 것이며, 이 두 막대는 서로의 뒤에 올 수 없는 경우이기 때문에 어떤걸 먼저 사용한다는 개념도 없어, 우리에게 어려움을 줍니다.
우리는 위와 같은 경우의 우선순위를 처리하기 위해, 특별한 조건으로 막대들을 나열해줄 필요가 있습니다.
만약 막대들을 길이를 기준으로 정렬한다면 어떤 일이 일어날까요? (4,9), (5,2), (2,1), (3,5), (1,4)의 막대들이 (1, 4), (2, 1), (3, 5), (4, 9), (5, 2)로 놓이게 될 것입니다. 혹시 다음과 같이 놓인 막대들에서 특별한 조건을 발견할 수 있을까요?
우리가 기계에서 다음으로 사용할 수 있는 막대는 항상 길이, 무게 모두 이전보다 크거나 같아야 한다는 조건이 있었습니다. 이 때, 우리가 길이 순서대로 막대를 정렬해놓는다면, 위 순서에서 뒤에 있는 막대들은 항상 앞에 있는 막대들보다 무게가 더 크다면, 그 막대 뒤에 사용할 수 있게 됩니다. (위 막대들은 길이 순으로 1 ≤ 2 ≤ 3 ≤ 4 ≤ 5를 만족하므로)
즉, 우리는 길이와 무게 2가지 조건을 고려하던 문제를, 길이 순으로 정렬하고 나면 무게만을 고려하는 문제로 바꿀 수 있습니다. (무게 4, 1, 5, 9, 2인 막대들을 사용하는 문제)
길이순으로 정렬한 이후, 우리는 문제를 다음과 같이 표상할 수 있습니다.
- 막대들의 무게가 길이 순서대로 주어져있을 때, 기계를 최소한으로 사용해서 가공하기
풀이
우리는 관찰 과정에서 문제에서 주어진 길이, 무게 조건 중 길이를 고려하지 않을 수 있도록 자료를 처리했습니다. 이제 주어진 무게들만을 이용하여 어떻게 문제의 답을 구할 수 있을까요?
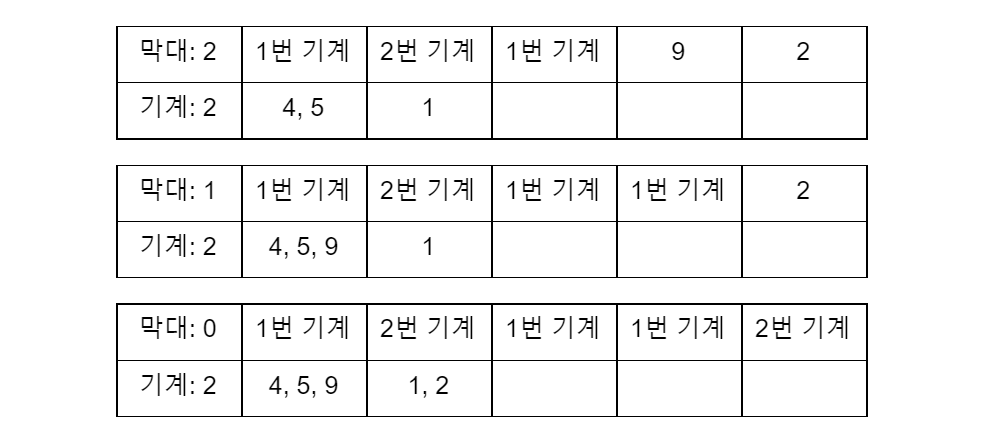
앞선 예시인 4, 1, 5, 9, 2인 막대가 길이 순으로 놓여있는 상황을 보겠습니다.
위 표는 현재 가공이 되지 않은 막대들과, 현재까지 사용한 기계의 수와 각 기계가 가공한 막대들을 나타내는 표 입니다 이제 각 막대를 무게가 4인 막대의 경우 4와 같이, 무게라는 단어를 빼고 부르겠습니다.
우리는 4인 막대를 다른 막대 뒤에 사용할 수 있을까요? 정답은 ‘그럴 수 없다’ 입니다. 위 막대들은 길이 순서대로 나열되어있고, 4는 길이가 가장 작은 막대이기 때문에, 그 이후에 다른 막대가 올 수 없습니다. 즉, 우리는 4를 처음으로 사용하는 기계가 적어도 하나 필요하다는 것을 알 수 있습니다.
그러므로, 우리는 1개의 기계를 준비하고, 그 기계에 4인 막대를 가공하도록 해야합니다.
이제 4개의 막대가 남고, 1개의 기계가 4인 막대를 가공하였습니다.
이 상태에서, 두 번째 막대인 1인 막대는 어떻게 될까요? 우리가 현재 존재하는 기계에서 가공을 할 수 있다면 새로운 기계를 들이지 않고 해결할 수 있으므로, 기존의 기계들을 살펴보겠습니다.
하지만 1번 기계는 4인 막대를 가공하였으므로, 1인 막대는 처리할 수 없습니다. 또한 1인 막대는 이 이후에 오는 막대들보다 항상 길이가 작기 때문에 다른 막대들을 먼저 처리하더라도 1인 막대를 가공할 수 없습니다.
즉, 우리는 막대들을 순서대로 보면서 남은 기계들이 현 막대를 처리할 수 없다면 새로운 기계를 사용하여 가공해줘야 합니다.
그렇다면 세번째 막대인 5는 어떨까요? 5인 막대는 앞선 막대들보다 길이도 더 길고, 무게도 크므로, 1번 기계와 2번 기계에서 모두 가공할 수 있습니다.
만약 이 막대를 2번 기계에서가공했다고 합시다. 그러고 나면 각 기계들은 항상 무게가 4, 5 보다 큰 막대들만 가공할 수 있게 되므로, 2, 3인 막대들은 처리할 수 없게 됩니다.
하지만 만약 이 막대를 1번 기계에서 가공한다면 어떻게 될까요? 각 기계들은 무게가 5, 1보다 큰 막대들만 가공할 수 있게 되므로, 2번 기계에서는 길이가 2, 3인 막대들을 처리할 수 있게 됩니다.
이 경우, 어떤 기계에서 5인 막대를 처리하더라도, 그 기계는 앞으로 5 초과인 막대들만 처리할 수 있게 되므로, 원래 그 막대가 1인 막대를 처리했든, 4인 막대를 처리했든 상관이 없게 됩니다. 우리는 가능한 이후에 더 많은 종류의 막대를 처리할 수 있도록 하고 싶으므로, 여러 기계가 처리할 수 있다면, 이전에 처리한 무게가 가장 큰 기계에서 가공하는 것이 좋습니다. (새로운 기계를 추가하는 것은, 이전에 0인 무게를 가공한 기계로 간주할 수 있기 때문에, 다른 기계를 사용할 수 있다면 그 기계를 사용하는 것이 항상 좋습니다.)
이제 위 규칙들에 맞추어 예시를 이어나가겠습니다.
이제 모든 경우가 끝나며, 우리는 주어진 예시가 2개의 기계, 즉, 2분에 처리가 가능함을 알 수 있습니다.
우리는 위 경우들을 통해서 다음과 같은 과정으로 문제를 처리해나가는 것이 최선이 됨을 확인할 수 있었습니다.
- 항상 길이 순서대로 막대를 가공해나간다.
- 만약, 현재 막대를 처리할 수 있는 기계가 없다면 새로운 기계를 추가한다.
- 여러 기계에서 막대를 처리할 수 있다면, 그 중 이전에 처리한 무게가 가장 큰 기계에서 가공한다.
우리가 막대들을 순서대로 처리해나갈 때, 위 경우들 이외에 상황이 발생하지 않는 다는 것은 어렵지 않게 알 수 있고(막대는 현재 기계들에서 가공할 수 있거나, 없거나 둘 중 하나이므로), 우리는 언제나 위 방법으로 정답을 찾을 수 있게 됩니다.
막대들을 정렬하는데 $O(NlgN)$, 각 $N$개의 막대들마다 자신을 가공할 기계를 찾는데 최대 $N$번의 탐색이 필요하므로, 우리는 $O(N^2)$에 문제를 해결할 수 있습니다.
ps. 만약 주어진 기계가 가공 가능한 길이와 무게의 조건이 $l ≤ l’$ 이며 $w ≤ w’$ 라면 어떻게 될까요? 이 경우 우리가 길이 순서대로 정렬하더라도, 항상 뒤에 있는 막대가 앞에 있는 막대보다 앞에 올 수 없다는 조건이 성립하지 않습니다.
하지만 우리가 제약조건을 약간 추가한다면, 위 상황도 우리가 진행했던 그대로 해결할 수 있게됩니다. 한 번 생각해보시길 바랍니다.
또한, 막대들마다 자신을 가공할 기계를 찾는 과정에서 완전이진탐색트리를 사용하는 방법으로 $O(lgN)$번의 탐색으로 사용할 기계를 찾아줄 수도 있어 $O(NlgN)$에도 해결할 수 있습니다.
쇼핑몰 - KOI 2019 1차대회 고등부 1번
관찰
실제로 위와 같은 쇼핑몰에서 계산이 진행된다면 어떤 식으로 이루어지게 될까요?
모든 사람들이 처음에는 줄을 서있다가, 가장 앞에 있는 사람부터 계산대에 자리가 남아있는지 확인하고, 만약 남아있는 자리가 있다면 이 중 가장 번호가 작은 계산대에 들어가게 될 것입니다.
이렇게 앞에 서있는 사람부터 계산대에 들어가다가, 만약에 계산대에 아무런 빈 자리가 없다면, 우리는 계산대에서 계산을 마치고 빈 자리가 날 때까지, 줄을 서있는 어떤 사람도 물건을 계산할 수 없게 됩니다.
즉, 우리는 다음과 같은 전략을 세워볼 수 있습니다.
- 계산대에 빈 계산대가 존재한다면 가장 앞에서부터 사람들을 채워넣는다
- 계산대에 빈 계산대가 존재하지 않다면 각 계산대에서 물건을 하나씩 계산하여 빈 계산대가 생길 때까지 계산을 진행하고, 동시에 빈 계산대가 생길 때에는 번호가 큰 계산대에서부터 손님이 나가도록 한다
- 빈 계산대가 생긴다면 줄의 가장 앞에 서 있는 사람을 가장 작은 계산대부터 다시 채워넣는다
- 줄에 아무런 사람도 서있지 않다면 모든 계산대에서 계산을 진행한다.
그렇다면, 이러한 방법으로 문제를 해결할 수 있을까요?
모든 $K$개의 계산대에 대해 여러 물건이 아닌 1개의 물건씩 계속해서 계산해주어야 하며, $N$명의 손님을 받을 수 있기 때문에 꽤 오랜 시간이 걸릴 수 있다는 생각을 해볼 수 있습니다.
우리가 문제에서 나올 수 있는 한 계산대가 최대로 계산해야하는 시간이 $NW$까지 나올 수 있다는 점과, 우리가 $K$개의 계산대에 대해 시뮬레이션 해야하므로, 꽤나 오랜 시간이 걸릴 수도 있을 것 같습니다.
그렇다면, 어떤 방법으로 문제를 생각해볼 수 있을까요?
우리는 주어진 문제를, 빈 계산대를 만들어 줄의 앞 사람을 추가하는 방식이 아니라, 처음부터 어떤 사람이 어느 계산대에서 계산할 지 알려주는 방법은 없을까요?
풀이
모든 줄을 서있는 사람들이 자신이 어떤 계산대에 서게 될지 배정해 줄 방법을 생각해봅시다.
우리는 어떤 사람이 이용할 계산대는 비어있는 계산대이기 때문에, 다르게 생각한다면 남아있는 물건의 양이 가장 적은 계산대를 사용하는 것으로 생각할 수 있습니다. 즉, 이를 이용하여 모든 사람들을 순서대로 계산대에 다음 조건을 만족하면서 배정해봅시다.
- 남아있는 물건이 가장 적은 계산대 중
- 가장 번호가 앞선 계산대
즉, 처음에 $K$명의 사람들을 모두 순서대로 계산대에 배정해주고 나면, $K+1$번 사람은 모든 계산대 중에 남은 물건이 가장 적고, 번호가 작은 계산대에 배정을 해주는 식으로 어떤 계산대에서 계산을 할지 먼저 알려주는 방법을 사용할 수 있습니다.
이 과정에서, $N$명의 사람들에 대해 $K$개의 계산대를 모두 확인하여 한 명씩 배정해주므로 총 $O(NK)$의 시간이 걸리게 됩니다.
그렇다면 계산대에서 빠져나갈 때에는 어떻게 될까요?
우리는 물건을 계산한 시간이 가장 이르고, 같은 경우 번호가 가장 큰 계산대부터 나간다는 사실을 알 수 있습니다. 즉, 다음을 고려해봅시다.
- $K$개의 계산대에 가장 앞에 서있는 사람 중
- 계산이 끝나는 시간이 가장 이른 사람들 중
- 번호가 가장 큰 계산대에 서 있는 사람
어차피 계산대의 뒤에 서 있는 사람은 앞에 서 있는 사람보다 더 늦게 계산이 끝나게 되므로, 우리는 위와 같은 방법으로 $K$개의 계산대를 확인 하는 것으로, 다음에 나갈 사람을 알 수 있게 됩니다.
이 때에도 총 $K$개의 계산대를 $N$번 보게 되므로, $O(NK)$의 시간이 들어 총 $O(NK)$에 문제를 해결할 수 있습니다.
허나 이러한 경우도 아직 문제를 빠르게 해결하기엔 느려보입니다. 그렇다면 어떤 방법을 이용해야 할까요?
우리는 이전에 다음 작업을 빠르게 하는 자료구조를 생각할 필요가 있습니다.
- N개의 원소 중 가장 작은 값을 $O(lgN)$에 구하는 자료구조
만약 위 작업을 사용할 수 있다면, 우리는 사람들을 계산대에 배정할 때에, $K$개의 계산대 중 가장 남아있는 물건이 적은 계산대를 $O(lgK)$에 구할 수 있고, 계산대에서 나오는 사람을 구할 때에도 가장 앞에 서 있는 최대 $K$명의 사람 중 가장 이르게 나오는 사람을 $O(lgK)$에 구해줄 수 있게 되어 총 $O(NlgK)$에 문제를 해결할 수 있게 됩니다.
우리는 위 연산을 할 수 있는 자료구조로 heap 구조를 사용할 수 있습니다. 이를 이용하면 충분히 빠른 시간을 갖는 시간복잡도를 구할 수 있어, 시간내에 문제를 해결할 수 있게 됩니다.
번외 풀이
사실 우리가 관찰에서 생각한 실제로 시뮬레이션을 통해 물건을 하나씩 계산하며 배정해주는 풀이는 한 사람이 가진 물건의 수가 작을 때에 꽤나 빠르게 동작한다는 사실을 알 수 있습니다.
관찰에서 엄밀히 언급하지는 않았지만, 우리가 우려했던 부분은 $N$명의 사람들이 있고 $K$개의 계산대가 있을 때에, 물건을 하나씩 시뮬레이션으로 계산하게 되므로 최악에 $K$개의 계산대에 대해 $NW$만큼의 시간을 시뮬레이션 해줘야하므로 $O(NKW)$ 만큼의 시간이 걸릴 수도 있을 것이라는 우려에서 시작합니다.
허나 실제로는 위 시간보다 훨씬 빠르게 동작합니다.
우리는 최대 $NW$만큼의 시간을 시뮬레이션 해야할 수도 있지만, 이 경우는 계산대가 하나 존재할 때에 발생합니다. 즉, $K$가 최대가 되는 상황에서도 $NW$의 시간이 유지가 되지는 않습니다.
잘 생각해보면 우리는 $K$개의 계산대가 존재할 때에, 최대로 오래 걸리는 계산대는 $NW / K + W$를 넘지 않는 다는 것을 알 수 있습니다. 모든 계산대들의 물건의 수 차이가 $W$보다 크다면, 가장 큰 계산대의 마지막 고객이 다른 계산대에서 줄을 서게 될 것이기 때문에, 모든 계산대는 $W$를 넘지 않는 선에서 고르게 물건이 분포되어야 합니다.
즉, 실제로 시뮬레이션 해줄 물건의 최대 수는 $NW / K + W$이므로, 우리가 고려할 최대 시간을 $O((NW / K + W) * K)$ = $O((N+K)W)$ 가 되어, 물건의 수가 충분히 작을 때에 꽤나 빠르게 문제를 해결 할 수 있습니다.
코드
나무 막대
#include <bits/stdc++.h>
using namespace std;
struct data{ int l, w; } arr[5010];
int T, n, m;
int warr[5010];
bool compare(data d1, data d2){ if(d1.l == d2.l) return d1.w < d2.w; return d1.l < d2.l; }
int main(){
int p, i, j, now, idx;
scanf("%d", &T);
for(p = 0; p < T; p++){
scanf("%d", &n);
for(i = 0; i < n; i++) scanf("%d %d", &arr[i].l, &arr[i].w);
sort(arr, arr + n, compare);
m = 1; warr[0] = arr[0].w;
for(i = 1; i < n; i++){
now = -1; idx = m;
for(j = 0; j < m; j++) if(warr[j] <= arr[i].w && warr[j] > now) now = warr[j], idx = j;
if(idx == m) warr[m++] = arr[i].w;
else warr[idx] = arr[i].w;
}
printf("%d\n", m);
}
return 0;
}
쇼핑몰
#include <bits/stdc++.h>
#define ll long long
using namespace std;
struct data{ ll a, s, d; };
struct cmp{
bool operator()(data d1, data d2){
if(d1.a == d2.a) return d1.s > d2.s;
return d1.a > d2.a;
}
};
int n, m;
priority_queue <data, vector<data>, cmp> pq1, pq2;
int main(){
int i;
ll a, s, res = 0;
data now;
scanf("%d %d", &n, &m);
for(i = 0; i < m; i++) pq1.push((data){0, i, 0});
for(i = 0; i < n; i++){
scanf("%d %d", &a, &s);
now = pq1.top(); pq1.pop();
pq1.push((data){now.a + s, now.s, a});
pq2.push((data){now.a + s, -now.s, a});
}
i = 1;
while(!pq2.empty()){
now = pq2.top(); pq2.pop();
res += i * now.d;
i++;
}
printf("%lld", res);
return 0;
}
쇼핑몰 - 번외풀이
#include <bits/stdc++.h>
#define ll long long
using namespace std;
struct data{ int v, idx; };
ll sum;
int n, k, cnt, ncnt = 1;
data arr[100010], counter[100010];
int main(){
int i, v, idx, flag = 1;
scanf("%d %d", &n, &k);
for(i = 0; i < n; i++){
scanf("%d %d", &idx, &v);
arr[i] = (data){v, idx};
}
for(i = 0; cnt < n && i < k; i++){
counter[i] = arr[cnt++];
}
while(flag){
flag = 0;
for(i = k - 1; i >= 0; i--){
if(counter[i].v) counter[i].v--, flag = 1;
if(!counter[i].v && counter[i].idx){
sum += 1ll * ncnt++ * counter[i].idx;
counter[i].idx = 0; flag = 1;
}
}
for(i = 0; cnt < n && i < k; i++){
if(!counter[i].v) counter[i] = arr[cnt++], flag = 1;
}
}
printf("%lld", sum);
}