cheetose's profile image

cheetose

August 22, 2021 00:00

서론

지난 글에서는 AWGN 채널의 특성에 대한 내용과, Probability of error 구하는 방법을, 혹시 정확한 계산이 어렵다면 그 상한을 계산하는 방법(Union Bound, Nearest Neighbor Union Bound)에 대해서 알아보았습니다.

이번 글에서는 현재 통신 시스템에서 사용하고 있는 constellation인 QAM과, 특정 주파수 사이의 신호만 통과시키는 passband system에 대해 알아보겠습니다. 아마 지금 passband system을 왜 설명하는지 헷갈릴 수 있지만, 나중에 작성할 글들을 이해하는 데에 있어 필수적인 내용이므로 꼭 이해하고 넘어가야 합니다.

본론

Quadrature Amplitude Modulation (QAM)

여태까지 저희가 알아본 변조 방식은 진폭만 조절하거나(PAM), 위상만 조절하거나(PSK), 주파수만 조절하는(FSK) 방식을 이용했습니다. 즉, 변조할 수 있는 파라미터 3개(진폭, 위상, 주파수) 중에서 1개만 적절히 조절해서 데이터를 변경해서 통신했습니다. 지금 알아볼 QAM은 위의 3개 중에서 진폭과 위상을 같이 조절해서 변조하는 방식을 말합니다. 2개의 PAM을 직교 상태로 결합시켰다고 생각하면 편할 것 같습니다. 따라서 QAM은 $2k$비트로 구성된 $2^{2k}$개의 심볼을 진폭과 위상으로 구별하게 됩니다.

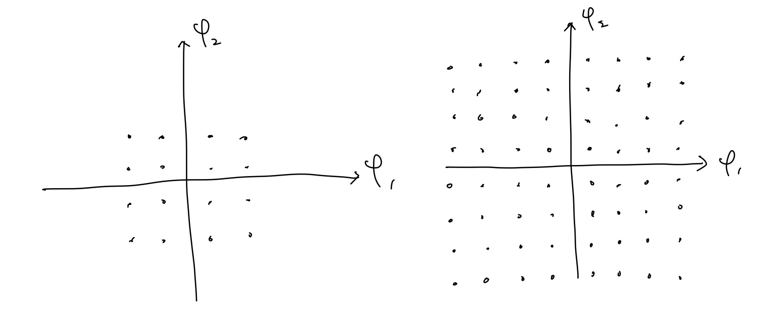
위는 16-QAM과 64-QAM의 constellation입니다. 현재 사용하고 있는 방식은 64-QAM 방식입니다. 32-QAM도 존재하지만, 그냥 이런 것이 있다는 것만 알고 넘어가면 될 것 같습니다. (16-QAM의 상하좌우에 4개의 심볼이 추가된 형태입니다.)

우선 M-QAM의 에러 발생 확률을 구해봅시다. 먼저 아래 그림과 같이 constellation을 3개의 부분으로 나누겠습니다. (Nearest Neighbor의 개수에 따라서 나눴습니다.)

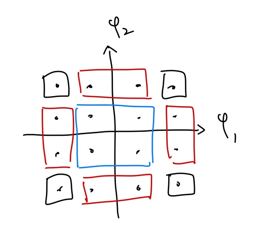
편의상 $Q \triangleq Q(\frac{d_{min}}{2\sigma})$로 정의하겠습니다. 우변의 의미는 이전 글에서 확인할 수 있습니다.

에러 발생 확률을 구하기 위해서는 정확한 추측을 할 확률을 구하고 그 값을 1에서 빼주면 됩니다. 따라서 그 확률 $P_c$를 구해보겠습니다.

• corner points (검은색 부분)

  

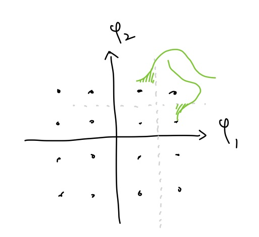
  $\psi_1$, $\psi_2$ 방향 모두 에러가 발생할 확률이 $Q$입니다. 따라서 에러가 발생하지 않을 확률은 $(1-Q)^2$입니다. 이러한 점이 4개 있습니다.

• edge points (빨간색 부분)

  

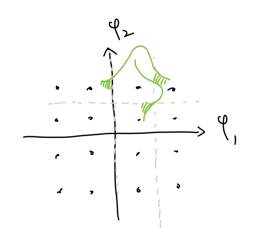
  $\psi_1$, $\psi_2$ 두 방향 중 한 방향으로는 에러가 발생할 확률이 $Q$, 다른 방향으로는 에러가 발생할 확률이 $2Q$ 입니다. 따라서 에러가 발생하지 않을 확률은 $(1-Q)(1-2Q)$ 입니다. 이러한 점이 $4 \times (\sqrt{M}-2)$개 있습니다.

• inner points (파란색 부분)

  

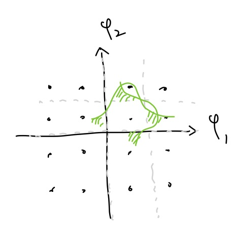
  $\psi_1$, $\psi_2$ 방향 모두 에러가 발생할 확률이 $2Q$입니다. 따라서 에러가 발생하지 않을 확률은 $(1-2Q)^2$입니다. 이러한 점이 $(\sqrt{M}-2)^2$개 있습니다.

이를 종합해보면

$P_c = \frac{1}{M} \times (4(1-Q)^2 + 4(\sqrt{M} - 2)(1-2Q)(1-Q) + (\sqrt{M}-2)^2 (1-2Q)^2)$

$=1-4(1-\frac{1}{\sqrt{M}})Q+4(1-\frac{1}{\sqrt{M}})^2Q^2$

여기서 $Q^2$은 매우 작은 값이므로 무시하면

$P_c \approx 1-4(1-\frac{1}{\sqrt{M}})Q$

$\therefore P_e = 1-P_c \approx 4(1-\frac{1}{\sqrt{M}})Q(\frac{d_{min}}{2\sigma})$

라는 결과를 얻을 수 있습니다.

위 과정을 NNUB를 통해서 구해보겠습니다.

corner points 의 경우, NN이 2이고, 이러한 점이 4개 있습니다. edge points 의 경우, NN이 3이고, 이러한 점이 $4 \times (\sqrt{M}-2)$개 있습니다. inner points 의 경우, NN이 4이고, 이러한 점이 $(\sqrt{M}-2)^2$개 있습니다. 따라서 $N_e = \frac{1}{M} (4 \times 2 + 4(\sqrt{M}-2) \times 3 + (\sqrt{M}-2)^2 \times 4) = 4(1-\frac{1}{\sqrt{M}})$ 이므로 위에서 구한 식과 정확히 같은 결과를 내는 것을 보았습니다.

여기를 잘 이해했으면 의문점이 하나 들어야합니다.

$M$이 커질 수록 에러가 발생할 확률이 줄어드는데 그럼 $M$을 무한히 크게 하면 좋은 거 아니야?

아쉽게도 에너지 관점에서 보면 $M$은 커질수록 불리해집니다. 왜 그런지 알아봅시다. 이에 대한 설명을 이해하기 위해 우선 1차원의 PAM을 통해 그 원인을 알아보고 이를 2차원으로 확장시켜보겠습니다. (미리 말씀드리자면, 유도 과정이 완벽히 동일합니다.)

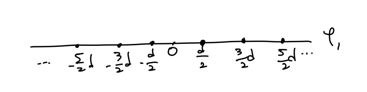
M-PAM의 constellation은 위 그림과 같습니다. 해당 constellation의 평균 에너지를 구하면

$\epsilon_x = \frac{2}{M} \sum_{k=1}^{M/2}(\frac{2k-1}{2})^2d^2 \text{(}\because \text{좌우 대칭)}$

$=\frac{d^2}{2M}\sum_{k=1}^{M/2}(2k-1)^2$

$=\frac{d^2}{12}(M^2-1)$

여기서 $M = 2^b$, ($b$는 비트 개수) 이므로 $M^2-1 = 2^{2b}-1$을 대입하면

$\epsilon_x = \frac{d^2}{12} \times 4^b -\frac{d^2}{12}$, 즉 비트 개수가 1개 늘어날 때마다 필요한 에너지가 약 4배 증가하는 것을 알 수 있습니다.

(참고: 보통 PAM에서 $\psi(t) = \frac{1}{\sqrt{T}}sinc(\frac{t}{T})$ ($sinc(x) = \frac{sin \pi x}{\pi x}$) 을 사용하는데, 이는 Nyquist condition을 만족하는 아무 함수로 설정한 것입니다. Nyquist condition은 OFDM에서 매우 중요한 조건으로, 추후에 다시 설명할 예정입니다.)

같은 방식으로 QAM에 대해서 계산해보겠습니다.

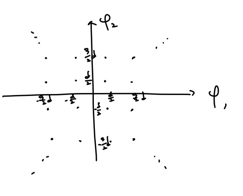
M-QAM의 constellation은 위 그림과 같습니다. PAM에서와 마찬가지로 위 constellation의 평균 에너지를 구하면

$\epsilon_x = \frac{1}{M}\sum_{i=1}^{\sqrt{M}} \sum_{j=1}^{\sqrt{M}}(x_i^2+x_j^2)$

$=\frac{1}{M}(\sqrt{M}\sum_{i=1}^{\sqrt{M}}x_i^2 + \sqrt{M}\sum_{j=1}^{\sqrt{M}}x_j^2)$

$=\frac{d^2}{6}(M-1) = 2\epsilon_{\sqrt{M}-PAM}$

따라서 QAM에서는 비트 개수가 1개 늘어날 때마다 필요한 에너지가 약 2배 증가합니다.

즉, $M$ 값을 키우면서 에러가 발생할 확률을 줄일 수 있지만, 그만큼 통신시에 더 많은 에너지가 들기 때문에 적절한 $M$ 값을 설정하는 것도 하나의 목표가 될 수 있습니다.

Passband systems

지금까지 설명했던 내용들은 통신을 하는 데에 있어서 모든 주파수 대역을 사용한다는 가정을 하고 내용을 설명했습니다. 하지만 모든 통신 시스템은 carrier frequency $\omega_c$ 중심으로 모여있습니다. 이를 passband system이라 합니다. 그리고 $\omega_c$ 중심으로 basis function이 이루어져 있으면 이를 passband modulation이라고 합니다. 여기서 중요한 점은 $\omega_c$가 채널의 bandwidth $W$보다 커야한다는 사실입니다. 곧 그림으로 설명할테지만, 그렇지 않으면 채널 대역이 음의 주파수 영역까지 도달하는 불상사(?)가 생길 수 있게됩니다. 예를 들어 CDMA 같은 경우에는 $\omega_c$= 1.9 GHz, $W$= 1.25 MHz 인 시스템이고, WCDMA는 $\omega_c$ = 2.1 GHz, $W$ = 5 MHz인 시스템입니다.

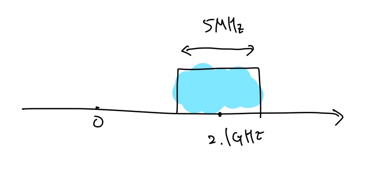
위의 그림처럼 WCDMA는 2.1 GHz를 중심으로 일정 범위의 주파수 대역만 사용할 수 있습니다. 이런 식으로 사용할 수 있는 주파수 대역을 제한 해놓는 모델을 bandlimited channel model이라 합니다.

이러한 passband signal의 큰 특징이 있습니다. 이는 시간 도메인에서의 신호 $x(t)$가 real function이면 이를 푸리에 변환한 함수 $X(\omega)$는 Hermitian function이라는 것입니다. Hermitian function은 $X(-\omega) = X^*(w)$를 만족하는 함수인데, 이를 풀어서 설명하면 magnitude는 even function이고, phase는 odd function이라는 것을 의미합니다.

우리는 이 어떤 carrier frequency를 중심으로 modulated된 신호 $x(t)$를 아래와 같이 표현할 것입니다.

• $x(t)=a(t)cos(\omega_c t + \theta(t))$

여기서 $a(t)$는 신호의 amplitude, $\omega_c$는 carrier frequency, $\theta(t)$는 phase입니다. 이를 전개하면 아래와 같습니다.

• $x(t) = a(t)cos(\theta(t))cos(\omega_c t) - a(t)sin(\theta(t))sin(\omega_c t)$

여기서 $a(t)cos(\theta(t))$를 $x(t)$의 inphase ($x_I(t)$), $a(t)sin(\theta(t))$를 $x(t)$의 quadrature ($x_Q(t)$)라고 정의하겠습니다. 그러면 $a(t)$와 $\theta(t)$를 다음과 같이 inphase와 quadrature로 표현할 수 있습니다.

• $a(t) = \sqrt{x_I^2(t) + x_Q^2(t)}$
• $\theta(t) = tan^{-1}(\frac{x_Q(t)}{x_I(t)})$

이를 이용하여 신호를 다른 방식으로 설명할 수 있는 표기법이 있는데, 이를 baseband equivalent signal 이라고 합니다. 해당 신호의 정의는 다음과 같습니다.

• $x_{bb}(t) \triangleq x_I(t) + j x_Q(t)$

위 식에서 볼 수 있듯이 해당 신호는 complex 신호입니다.

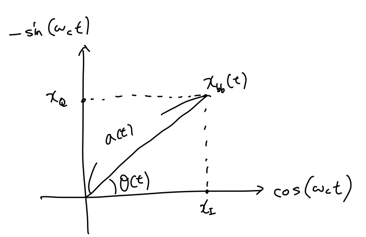
x축을 $cos(\omega_c t)$, y축을 $-sin(\omega_c t)$로 했을 때, $x_{bb}(t) \text{, } x_I(t)\text{, } x_Q(t)\text{, } a(t)\text{, } \theta(t)$의 관계를 위의 그림처럼 정리할 수 있습니다.

Hilbert transform

Hilbert transform은 잠시 뒤에 나올 신호의 또 다른 표현법인 Analytic equivalent signal을 구하는 데에 사용되는 변환법입니다.

이는 $\bar{h} = \begin{cases} \frac{1}{\pi t} & \text{if } t \neq 0 \ 0 & \text{else} \end{cases}$ 를 $x(t)$와 convolution 시키는 변환이며, 변환된 결과를 $\check{x}(t) = x(t) * \bar{h}(t)$ 로 정의합니다. 이를 직접 계산하기는 어렵기 때문에 약간의 트릭을 사용할 것입니다. $sgn(t)$의 Fourier transform 결과가 $\frac{2}{jw}$ 이므로, Fourier transform의 duality 관계 ($x(t) \leftrightarrow X(w) \text{일 때, } X(t) \leftrightarrow 2\pi x(-w)$)를 이용하면 $\frac{1}{\pi t}$의 Fourier transform 결과는 $-j \text{ } sgn(w)$ 가 됩니다. 그러므로 $\check{X}(w) = -j\text{ }sgn(w)X(w)$ 라는 아주 간단한 식을 통해서 $x(t)$의 hilbert transform을 구할 수 있습니다.

조금 더 살펴보자면 $\check{x}(t)$의 hilbert transform은 $-x(t)$가 되고, $\bar{h}(t)$의 역함수는 $-\bar{h}(t)$가 되는데, 이는 $\bar{H}(w)^2 =-1$임을 이용해서 쉽게 유도할 수 있습니다.

Analytic equivalent signal

앞에서 언급했듯이, $\check{x}(t)$을 이용하여 신호를 표현하는 방식을 Analytic equivalent signal이라 하고 그 정의는 다음과 같습니다.

• $x_A(t) \triangleq x(t) + j\check{x}(t)$

결론부터 말하자면 $x_{bb}(t) = x_A(t)e^{-j\omega_c t}$를 만족합니다. 즉, $x_A(t)$는 복소평면 상에서 $x_{bb}(t)$를 반시계 방향으로 $\omega_c t$ 만큼 회전시킨 것을 의미합니다.

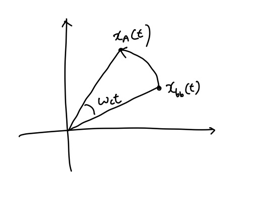
지금부터 위의 식이 성립함을 설명하겠습니다.

우선 $x(t) = x_I(t)cos(\omega_c t)-x_Q(t)sin(\omega_c t)$를 푸리에 변환을 하면

$X(\omega) = \frac{1}{2}(X_I(\omega+\omega_c)+X_I(\omega - \omega_c)) - \frac{1}{2j}(X_Q(\omega-\omega_c)-X_Q(\omega+\omega_c))$ 를 구할 수 있고, 이를 hilbert transform 해주면

$\check{X}(\omega) = X(\omega)\bar{H}(\omega) = -\frac{j}{2}(-X_I(\omega + \omega_c)+X_I(\omega - \omega_c))+\frac{1}{2}(X_Q(\omega-\omega_c)+X_Q(\omega + \omega_c))$ 입니다. 여기서 푸리에 역변환을 하면

$\check{x}(t) = x_I(t)sin(\omega_c t)+x_Q(t)cos(\omega_c t)$ 를 얻을 수 있습니다. 이제 이 값을 $x_A(t)$에 대입해서 실수부와 허수부로 나눠 정리해주면

$x_A(t) = [x_I(t)cos(\omega_c t)-x_Q(t)sin(\omega_c t)] + j[x_I(t)sin(\omega_c t)+x_Q(t)cos(\omega_c t)]$

$=(x_I(t)+jx_Q(t))(cos(\omega_c t)+j\text{ }sin(\omega_c t))$

여기서 $(x_I(t)+jx_Q(t)) = x_{bb}(t)$ 이고, $(cos(\omega_c t)+j\text{ }sin(\omega_c t)) = e^{j\omega_c t}$ 이므로 $x_A(t) = x_{bb}(t)e^{j\omega_c t}$ 가 되고, 위의 식이 성립함을 알 수 있습니다.

즉, 저희는 $x(t)$를 알면 $a(t)$와 $\theta(t)$를 알 수 있고, 이를 알면 $x_I(t)$와 $x_Q(t)$를 알 수 있고, 이를 통해 $x_{bb}(t)$와 $x_A(t)$를 구할 수 있습니다. 즉, 아무거나 하나만 알아도 자유로운 변환이 가능합니다.

$x(t), x_A(t), x_{bb}(t)$를 주파수 영역에서 보면 그 특징을 확인할 수 있습니다. $x_A(t) = x(t)+j\check{x}(t)$를 푸리에 변환하면

$X_A(\omega) = X(\omega) + j(-j\text{ }sgn(\omega)X(\omega)) = (1+sgn(\omega))X(\omega) = \begin{cases} 2X(\omega) & \text{if } \omega > 0 \ 0 & \text{else} \end{cases}$

또한 $x_{bb}(t) = x_A(t)e^{-j\omega_c t}$를 푸리에 변환하면

$X_{bb}(\omega) = X_A(\omega + \omega_c)$ 입니다. 이를 그림으로 표현하면 아래 그림과 같습니다.

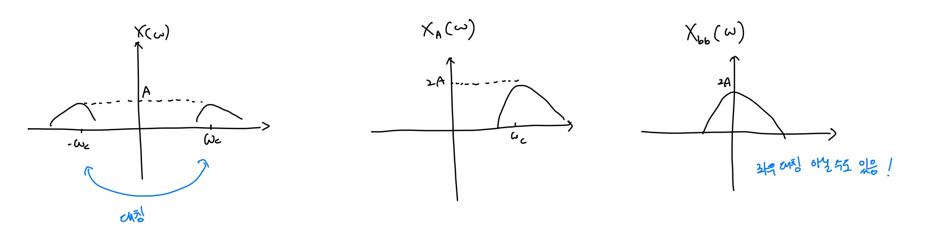
이제 말하는 사실이지만 $X_{bb}(\omega)$는 정보가 DC$(\omega = 0)$을 중심으로 모여있기 때문에 baseband라고 말하는 것입니다.

결론

이번 글에서는 QAM과 passband 시스템에 대해서 알아보았습니다. 앞으로 passband 시스템에서 사용한 표현법을 자유자제로 사용할 예정이기 때문에 앞으로의 글을 이해하기 위해서는 오늘 글을 이해하고 넘어갔으면 하는 바람이 있습니다.

다음 글에서는 주로 ISI(신호간 간섭)와 Nyquist criterion에 관한 내용을 다룰 예정입니다. 미리 말씀을 드리자면 통신 속도를 빠르게 하면 ISI가 커지고, 대부분 통신 에러는 이 ISI 때문에 생기게 됩니다. 그렇기 때문에 ISI를 줄이는 것이 통신 세대가 4G, 5G로 넘어갈수록 점점 더 큰 과제가 되고 있습니다.

Reference

• Fundamentals of Communication Systems, John G Proakis