Wireless Digital Communication 4
서론
지난 글에서는 QAM과 Passband 시스템, 그리고 하나의 신호를 표현하는 여러가지 방식들에 대해서 알아보았습니다.
이번 글에서는 ISI와 Nyquist criterion에 대해서 작성할 것입니다. 제가 이 시리즈를 쓰고 있는 최종 목표인 OFDM 자체가 ISI를 줄이기 위함이고, 이를 위해서 Nyquist condition 을 만족해야합니다. 따라서 이번 글이 제가 생각하기에 가장 중요한 내용 중 하나라고 생각합니다.
본론
Intersymbol Interference (ISI)
저희는 지금까지 어떤 신호를 표현할 때 $x(t) = \sum_{k=0}^{K-1} x_k \psi(t-kT)$, 즉 가중치가 있는 basis function을 연속적으로 나열한 형태로 표현했습니다. basis function $\psi(t-kT)$이 orthogonal하기 때문에 변조와 복조가 용이했다는 사실을 기억하실 겁니다. 하지만 이는 $x(t)$가 지나는 채널이 존재하지 않음을 가정했을 때의 경우이고, 현실적으로 신호는 아래 그림처럼 항상 어떠한 채널 $h(t)$를 지나게 됩니다. 이 경우에는 $\psi(t-kT)$의 orthogonality가 보장되지 않기 때문에 변조/복조가 더욱 어려워집니다.
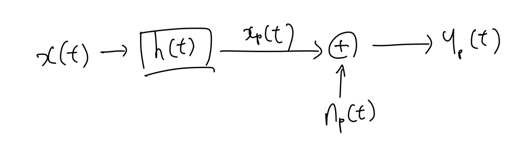
위 도식에서 $x_p(t) = x(t) * h(t)$인데, $x(t) = \sum_{k=0}^{K-1} \sum_{n=1}^{N} x_{kn} \psi_n(t-kT)$ 이므로
$x_p(t) = \sum_{k=0}^{K-1} \sum_{n=1}^{N} x_{kn} \psi_n(t-kT) * h(t)$ 로 표현할 수 있습니다. 여기서 $\psi_n(t) * h(t) = p_n(t)$로 정의하면 $x_p(t) = \sum_{k=0}^{K-1} \sum_{n=1}^{N} x_{kn} p_n(t-kT)$ 로 표현할 수 있습니다. 이 과정을 하나로 합치면 아래처럼 표현할 수 있습니다.
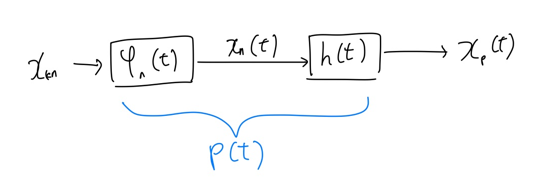
사실 이러한 신호를 송신할 때 주기를 굉장히 길게 해서 보내면 수신단에서도 복조가 그리 어렵지는 않을 겁니다. 하지만 통신의 목표 중 하나는 data rate ($R=\frac{b}{T}$)를 키우고, symbol period ( $T$ )를 줄이는 것입니다. 그 결과 신호와 신호 사이에 겹치는 부분이 발생하여 ISI (신호간 간섭)이 발생하게 됩니다.
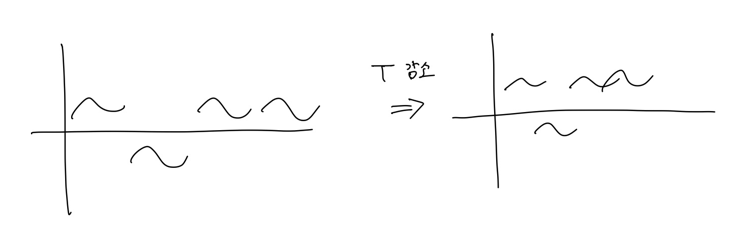
왼쪽 그림은 $T$가 큰 상황, 오른쪽 그림은 $T$가 작아 ISI가 발생한 상황의 예시입니다.

위 그림은 ISI 채널 모델을 도식화한 것입니다. 여기서 $\psi_p(t)$는 $p(t)$를 normalize한 함수, 즉 $\psi_p(t) = \frac{p(t)}{\vert p \vert}$입니다. 위 도식을 따라가며 $y(t)$을 구해보면 그 식은 아래와 같습니다.
$y(t) = \sum_k \vert p \vert x_k \psi_p(t-kT)* \psi_p^(-t) + n_p(t) * \psi_p^(-t)$
여기서 $\psi_p(t) * \psi_p^(-t) = q(t), n_p(t) * n_p^(-t) = n(t)$ 로 정의하면 $y(t) = \sum_k \vert p \vert x_k q(t-kT) + n(t)$로 정리할 수 있습니다. 그리고 이 함수를 $t=kT$에 대해 샘플링한 결과가 $y_k$가 됩니다. 여기서 중요한 사실이 있는데, $y(t)$를 샘플링해서 $y_k$를 구했는데 이 때 정보 손실이 전혀 없습니다. 따라서 $y(t)$ 대신에 $y_k$를 이용해서 정보들을 처리해도 전혀 문제가 없습니다.
$y_k$를 식으로 표현하면 아래와 같습니다.
$y_k = y(t) \vert {t=kT} = \sum_m \vert p \vert x_m q(kT-mT) + n(kT) = \sum_m \vert p \vert x_m q{k-m} + n_k$
$ = \vert p \vert x_k * q_k + n_k$
$ = \vert p \vert (\cdots + q_{-1} x_{k+1} + q_0 x_k + q_1 x_{k-1} + \cdots) + n_k$
여기서 $q(t)$가 Hermitian function 이므로 $q_0 = 1$입니다. 따라서
$y_k = \vert p \vert x_k + \vert p \vert \sum_{m \neq k} x_m q_{k-m} + n_k$ 로 표현할 수 있습니다.
위 식에서 $\vert p \vert \sum_{m \neq k} x_m q_{k-m}$에 해당하는 부분이 $y_k$에 대한 ISI 입니다. ($x_k$ 이외의 신호에서 영향을 받아 이상적으로는 $x_k$만 와야하는데, 간섭이 일어납니다.)
Nyquist criterion
Nyquist criterion에 대해 설명하기에 앞서 Discrete time Fourier transform (DTFT)에 대해 잠깐 설명하고 가겠습니다.
$x_a(t)$를 푸리에 변환한 결과를 $X_a(\omega) = \int_{-\infty}^{\infty} x_a(t)e^{-jwt} dt$라고 했을 때, $x_a(t)$는 $X_a(\omega)$의 푸리에 역변환으로, $x_a(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X_a(\omega)e^{jwt} d\omega$ 입니다. (여기서 $a$는 아날로그 신호임을 의미합니다.)
$x_a(t)$를 $t=kT$에 대해 샘플링한 결과가 $x_k = x_a(kT)$라고 했고, 이를 $x[k]$라고 표현하겠습니다. 그러면 $x[k]$는 위 결과에 $t=kT$를 대입한 결과와 같으므로
$x[k] = x_a(kT) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X_a(\omega)e^{jwkT} d\omega$
$ = \frac{1}{2\pi} \sum_{n = -\infty}^{\infty} \int _{\frac{(2n-1)\pi}{T}}^{\frac{(2n+1)\pi}{T}} X_a(\omega) e^{jwkT} d\omega$ ($-\infty$ 부터 $\infty$ 의 구간을 주기 $T$의 무한한 구간으로 나눴습니다.) 여기서 $\omega - \frac{2n\pi}{T} = \omega’$으로 치환하면
$x[k] =\frac{1}{2\pi} \sum_{-\infty}^{\infty} \int_{-\frac{\pi}{T}}^{\frac{\pi}{T}} X_a(\omega’ + \frac{2n\pi}{T}) e^{j(\omega’ + \frac{2n\pi}{T})kT} d\omega$ 이고, $e^{j(\omega’ + \frac{2n\pi}{T})kT} = e^{j\omega’kT} \cdot e^{j2\pi nk} = e^{j\omega’kT} (\because e^{j2\pi nk} = 1)$ 이므로
$x[k] = \frac{1}{2\pi} \sum_{-\infty}^{\infty} \int_{-\frac{\pi}{T}}^{\frac{\pi}{T}} X_a(\omega + \frac{2n\pi}{T}) e^{j\omega kT} d\omega$ 가 됩니다.
이번엔 다른 방식으로 $x[k]$에 대한 식을 구해보겠습니다. DTFT의 정의에 의해 $X(e^{j\Omega}) = \sum_{k = -\infty}^{\infty} x[k]e^{-j\Omega k}$ 이고 이를 역변환하면 $x[k] = \frac{1}{2\pi} \int_{-\pi}^{\pi} X(e^{j\Omega}) e^{j\Omega k} d\Omega$ 입니다. 구간이 [$-\pi, \pi$]인 이유는 $e^{j\Omega}$의 주기가 $2\pi$이기 때문입니다. 여기서 $\omega = \frac{\Omega}{T}$ 를 대입하면 $x[k] = \frac{T}{2\pi} \int_{-\frac{\pi}{T}}^{\frac{\pi}{T}} X(e^{j\omega T})e^{j\omega Tk} d\omega$ 를 구할 수 있습니다.
이를 앞에서 구한 식과 비교를 해보면
$X(e^{j\omega t}) = \frac{1}{T} \sum_{n= -\infty}^{\infty} X_a(\omega + \frac{2n\pi}{T})$ 라는 등식을 얻을 수 있고, 두 식의 주기는 모두 $\frac{2\pi}{T}$입니다.
이를 이용하여 $q_k = q(kT) = \frac{1}{2\pi} \sum_{n = -\infty}^{\infty}\int_{-\frac{-\pi}{T}}^{\frac{\pi}{T}} Q(\omega + \frac{2n\pi}{T}) e^{j\omega kT} d\omega$ 를 구할 수 있습니다. 여기서 $\sum_{n = -\infty}^{\infty} Q(\omega + \frac{2n\pi}{T})$ 는 equivalent frequency response 라고 하며 이를 $Q_{eq}(\omega)$로 정의했습니다. 이를 앞에서 구했던 등식에 적용하면 $\frac{1}{T} Q_{eq}(\omega) = Q(e^{j\omega t}) = \sum_{k = -\infty}^{\infty} q_k e^{-j\omega kT}$ 를 구할 수 있습니다.
앞에서 ISI의 정의가 $\vert p \vert \sum_{m \neq k} x_m q_{k-m}$ 라고 했습니다. 즉, $m \neq k$ 에 대해서 $q_{k-m} = 0$이면 ISI는 발생하지 않습니다. 즉, $q_k = \delta_k$이면 ISI가 발생하지 않는다는 뜻이고, 이는 더 간단하게 $Q(e^{j\omega T}) = 1$이면 ISI가 발생하지 않는다는 것을 의미합니다.
이를 만족하는, 즉 주파수 영역에서의 함수가 상수인 신호들을 Nyquist pulse라 하고, 모든 Nyquist pulse는 ISI가 발생하지 않습니다.
가장 대표적인 Nyquist pulse는 sinc 함수입니다. sinc 함수는 $sinc(t) = \frac{sin(\pi t)}{\pi t}$로 정의되는 함수입니다.

$sinc(\frac{t}{T})$은 왼쪽과 같은 함수인데, 이를 푸리에 변환을 하면 $T \sqcap(T\omega)$로 오른쪽 형태의 함수를 띄게 됩니다. 모든 신호를 합치면 빨간 선에 해당하는 신호가 만들어지는데 이는 상수값으로 Nyquist criterion을 만족합니다. (참고로 sinc 함수는 모든 Nyquist pulse 중에서 bandwidth가 가장 작습니다.)
하지만 이렇게 완벽히 딱딱 들어맞게 만들기는 어렵기 때문에 그 대안책으로 Raised cosine pulse를 이용합니다. 이 함수에 대한 설명은 아래 그림을 통해 하겠습니다.
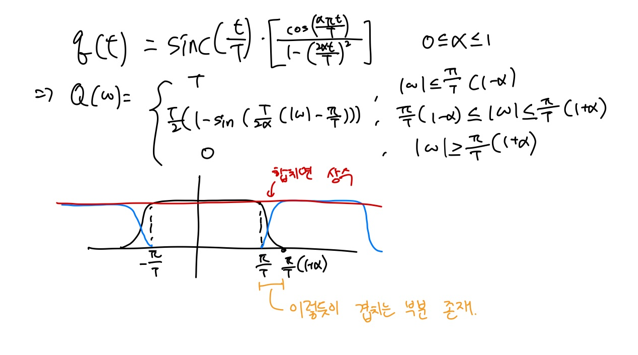
결론
이번 글에서는 ISI가 무엇인지, 그리고 ISI를 없앨 수 있는 조건인 Nyquist criterion이 무엇인지에 대해 설명했습니다.
이번 글까지 해서, 최종 목표인 OFDM이 무엇인가? 를 공부하기 위해 알아야만 하는 내용들을 다뤘습니다. 다음 글부터는 본격적으로 OFDM에 관련하여 글을 작성하도록 하겠습니다.
Reference
- Fundamentals of Communication Systems, John G Proakis