Wireless Digital Communication 5
서론
지난 글에서는 ISI와 Nyquist criterion에 대해 설명을 했습니다. 지난 글까지 잘 따라오셨다면 OFDM을 공부하기 위한 기초적인 지식을 다 공부한 것입니다.
이번 글과 다음 글, 두 번에 걸쳐 OFDM에 대한 내용을 다룰 예정입니다. 이번 글에서는 OFDM이란 무엇인가, 그리고 DFT/IDFT와 어떤 관계가 있는가에 대해서 다룰 예정입니다.
본론
OFDM은 Orthogonal Frequency Division Multiplexting의 약자로, FDM은 FDM인데 신호들을 Orthogonal 하게 중첩시켜 Bandwidth를 절반 정도로 줄인 기법을 의미합니다. FDM은 어떤 주파수 대역을 겹치지 않는 하부 대역으로 나눠 분리된 대역을 각각 1개의 신호를 전달하는데 사용하는 기술입니다.
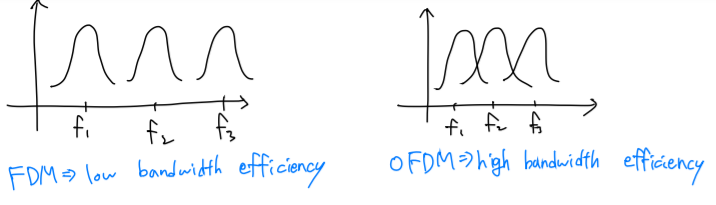
위 그림에서 알 수 있듯이 FDM과 비교했을 때 OFDM은 같은 주파수 대역에 더 많은 신호를 전달할 수 있어 효과적입니다.
Discrete Fourier tranform (DFT)
OFDM은 기본적으로 DFT를 사용합니다. DFT 관련된 내용은 여기서 공부하실 수 있습니다. DFT가 OFDM을 설명하는 도구로 이용되는만큼 자세한 내용을 설명하진 않겠으나 핵심적인 내용만 요약해서 설명하고 넘어가겠습니다.
길이가 $N$인 $x[n]$과 $h[n]$의 circular convolution은 $x[n] \circledast h[n]$ 으로 표현하고, 그 결과는 $y_c[n] = \sum_{m=0}^{N-1} h[m]x[(n-m)\%N]$ 입니다. 이 때 $(n-m)\%N$이 음수라면 자연스럽게 $N$을 더해주시면 됩니다. 예를 들어 $x[n]= {1, 2, 0, 1}, h[n] = {2, 2, 1, 1}$ 이라면 $y_c[n] = {6, 7, 6, 5}$ 가 됩니다.
$x[n]$을 DFT하면 $X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N}$ 이고 $X[k]$를 IDFT하면 $x[n] = \frac{1}{N} \sum_{n=0}^{N-1} X[k]e^{j2\pi kn/N}$이 됩니다. 또한 $x[n]$과 $h[n]$의 circular convolution인 $y_c[n]$을 DFT한 결과는 $Y_c[k] = H[k]X[k]$가 되고, $y_c[n]$은 $H[k]X[k]$를 IDFT 함으로써 구할 수 있습니다.
DFT를 하는데 $O(N^2)$의 시간복잡도가 필요하지만, FFT를 사용하면 $O(N log N)$의 시간복잡도로 계산할 수 있으며, OFDM은 이 FFT를 활용한 기술입니다.
OFDM

OFDM은 송신부에서 기본적으로 위 그림처럼 데이터들을 병렬로 처리해서 보냅니다. 여기서 ${\psi_n(t) }$는 orthogonal set이고, $\psi_i(t) = e^{j2\pi(f_c + k \Delta f)t}$ 입니다.
passband signal $s(t)$는 $d_k$와 $\psi_k(t)$의 곱의 합으로 표현 가능합니다. 이를 식으로 표현하면 $Re{ \sum_{k=0}^{N-1} d_k e^{j2\pi (f_c + k \Delta f)t} w(t)}$ 가 됩니다. 여기서 $d_k$는 $k$번 째 송신 신호이고, $w(t)$는 window function입니다. window function은 일부 구간을 제외하고는 전부 0으로 만들기 위해 곱해주는 함수입니다. 주파수 대역에서의 filter와 비슷한 개념이라고 생각하시면 되겠습니다. 본 글에서는 주로 rectangular window를 이용할 것입니다.
이전 글에서 어떤 신호를 baseband equivalent signal를 이용해 $s(t) = Re{s_b(t)e^{j2\pi f_c t}}$로 표현할 수 있음을 배웠습니다. 따라서 이걸 위 신호에 대입하면 $s_{bb}(t) = \sum_{k=0}^{N-1} d_k e^{j2\pi k \Delta ft} w(t)$ 라는 식을 유도할 수 있습니다. $e^{j2\pi f_0 t} x(t)$를 푸리에 변환 하면 $X(f-f_0)$이 되는 점을 이용하면 $s_{bb}$를 푸리에 변환 했을 때 $S_{bb}(f) = \sum_{k=0}^{N-1} d_k W(f-k \Delta f)$가 됩니다. 이를 그림으로 그려보면 아래와 같습니다.
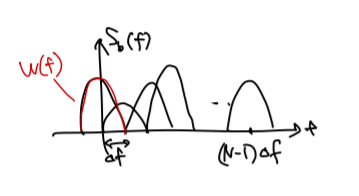
위에서 $d_k$가 전부 다른 값이기 때문에 각 $W(f)$의 magnitude 역시 달라질 수 있습니다.

지금까지 했던 내용들을 바탕으로 $s(t)$를 구하기 위한 과정을 위 도식처럼 살짝 바꿔보겠습니다. 이제 $e^{j2\pi m \Delta ft}$를 $m$번 째 basis function, $\psi_m(t)$로 생각할 수 있습니다. symbol period가 T일 때, ${e^{j2\pi m \Delta ft}}$가 orthogonal set이 되기 위해선 $\Delta fT$가 정수 꼴이어야 합니다.
$\psi_m(t) = e^{j2\pi m \Delta ft}$라고 할 때, orthogonality를 만족하려면 $\int_0^T \psi_k(t) \psi_m^*(t) dt = T \delta_{k-m}$ 이어야합니다.
$\int_0^T \psi_k(t) \psi_m^*(t) dt = \int_0^T e^{j2\pi k \Delta ft} \int_0^T e^{-j2\pi m \Delta ft} dt = \int_0^T e^{j2\pi (k-m) \Delta ft} dt$
$k = m$일 때, $\int_0^T 1 dt = T$
$k \neq m$일 때, $\frac{e^{j2\pi (k-m) \Delta ft}}{j2\pi (k-m) \Delta f} \vert_{t=0}^T = \frac{e^{j2\pi (k-m) \Delta fT} -1}{j2\pi (k-m) \Delta f}$ 인데, $\Delta fT = l$ ($l$은 정수) 일 때만 해당 값이 0이 됩니다.
따라서 우리는 $\Delta fT$가 정수가 되는 $\Delta f$를 정해야하고, 실제 OFDM 시스템에서는 가장 효율적인 bandwidth를 위해 $\Delta f = \frac{1}{T}$를 선택했습니다.
지금까지는 OFDM의 송신단에 대한 이야기를 해봤습니다. 이제 송신단에서 $s_bb(t)$를 보냈다고 하면, 과연 수신단에서는 이를 어떻게 처리할까요? 예전에 단순한 신호를 송수신했을 때와 마찬가지로, 이번에도 역시 basis function의 complex conjugate를 곱해준 뒤 해당 구간을 적분하면 됩니다. 이를 도식화 하면 아래 그림과 같습니다.
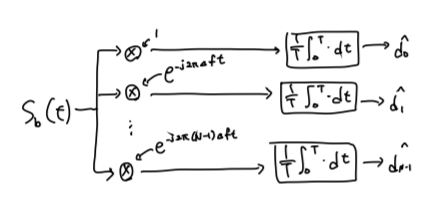
지금부터는 주파수 대역에서의 내용을 살펴보겠습니다.
매우 간단한 window function인 $w(t) = 1, 0 \leq t \leq T$ 라고 가정합시다. 그러면 m번 째 output인 $\hat{d_m}$은 다음과 같이 구할 수 있습니다.
$\hat{d_m} = \frac{1}{T} \int_0^T e^{-j2\pi m \Delta t} \sum_{k=0}^{N-1} d_k e^{j2\pi k \Delta ft} dt = \frac{1}{T} \sum_{k=0}^{N-1} d_k \int_0^T e^{j2\pi (k-m) \Delta ft} dt$
여기서 $\int_0^T e^{j2\pi (k-m) \Delta ft} dt$에 해당하는 부분이 $T \delta_{k-m}$이므로 $\hat{d_m} = d_m$이라는 결과를 얻을 수 있습니다.
앞에서 $w(t) = 1, 0 \leq t \leq T$라는 가정을 했습니다. 이를 푸리에 변환해보면 $W(f) = sinc(fT) e^{(\cdot)}$ 이 됩니다. $e^{\cdot}$으로 표현한 이유는 지금 설명할 내용은 phase보다 magnitude에 초점이 맞춰져 있기 때문이고, 고로 해당 부분을 무시하고 설명하겠습니다.
아무튼 이 내용을 바탕으로 기존 $\sum_{k=0}^{N-1} d_k e^{j2\pi kt/T} w(t)$를 푸리에 변환하면 $\sum_{k=0}^{N-1} d_k sinc(Tf-k)$가 됩니다. 이를 그림으로 표현하면 아래와 같습니다.
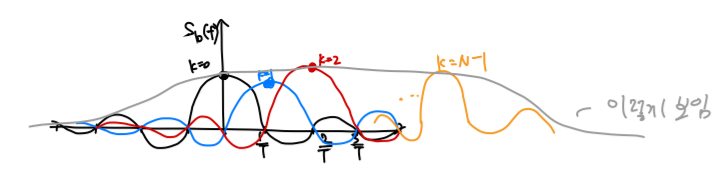
여기서 어떤 구간 T에서 사인파의 주기가 T/정수 꼴이라면 각 사인파들은 서로 orthogonal 하다는 사실을 통해 위 신호가 orthogonal한 신호라는 것을 알 수 있습니다. 해당 내용의 증명은 다음과 같습니다.
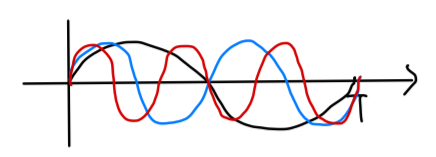
$\int_0^T cos(\frac{2\pi kt}{T}) cos(\frac{2\pi mt}{T} + \theta) dt = \frac{T}{2} \delta_{k-m} cos \theta$ . 즉, $k \neq m$ 이면 항상 이 값은 0이 되기 때문에 서로 다른 신호가 orthogonal 하다는 것을 알 수 있습니다.
또한 $\sum_{k=0}^{N-1} d_k sinc(Tf-k)$ 의 그림을 보면 각 subcarrier의 극점에서 자기 자신을 제외한 subcarrier는 0임을 알 수 있고, 이는 곳 subcarrier 간의 간섭이 일어나지 않아 Nyquist criterion을 만족하고, intercarrier interference(ICI, carrier간 간섭)이 없음을 알 수 있습니다.
송신단에서의 이산 신호 표현
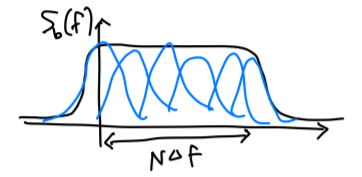
N개의 subcarrier의 신호를 모두 더하면 $s_{bb}(t)$는 위의 그림처럼 보일 것입니다. 이 때 $\Delta f = \frac{1}{T}$입니다. 기존에 알고있던 지식 상에서, 이 신호를 alias가 나타나지 않도록 (Nyquist condition을 만족하도록) 샘플링을 하기 위해서는 $f_s$를 $2f_m$으로 잡아야합니다. 이 때 $f_m$은 신호의 최대 주파수로, 위 상황에서는 $N \Delta f$를 의미합니다.
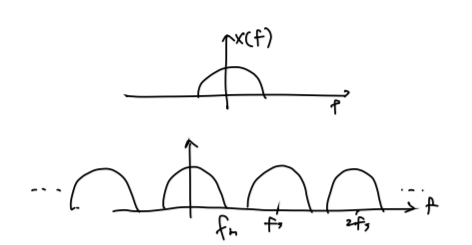
사실 $f_s$를 $2f_m$으로 잡는 이유는 위와 같은 이유에서였지만

이런 식으로 양의 주파수 대역만 사용하는 경우에는 $f_s$가 $f_m$이 되어도 충분히 alias 없이 원래 신호로 복원이 가능해집니다. 우리는 앞으로 이러한 상황을 고려할 것입니다.
이를 이용하여 위 신호를 샘플링해보겠습니다. $f_m = N \Delta f = \frac{N}{T}$ 이므로 $f_s$ 역시 $\frac{N}{T}$입니다. 샘플링된 신호를 $s_n$이라고 하면, $s_n$은 다음과 같이 표현할 수 있습니다.
$s_n = s_{bb}(t) \vert_{t = n/f_s = nT/N} = \sum_{k=0}^{N-1} d_k e^{j \frac{2\pi k}{T} \frac{nT}{N}} = \sum_{k=0}^{N-1} d_k e^{j2\pi kn/N}$
이는 $d_k$의 IDFT 형태입니다. 즉, 각각 따로 샘플링하는 대신에 IDFT를 해주면 모든 $d_k$에 대한 샘플을 구할 수 있습니다.
수신단에서의 이산 신호 표현
$m$번 째 수신단에서는 $\hat{d_m} = \int_0^T s_{bb}(t) e^{-jw\pi mt/T} dt$라는 신호를 받습니다. 마찬가지로 이를 $t=\frac{nT}{N}$에 대해 샘플링 해보면 $\sum_{n=0}^{N-1} s_n e^{-j2\pi nm/N}$ 이 되는데, 이는 $s_n$에 대해서 DFT를 한 결과입니다.
앞서 언급했던대로 일반적인 방법으로 IDFT와 DFT를 하기 위해서는 $O(N^2)$의 시간복잡도가 필요하지만, FFT를 이용하면 $O(NlogN)$이라는 시간복잡도에 두 작업을 할 수 있습니다.
지금까지 알아본 과정을 도식화 하면
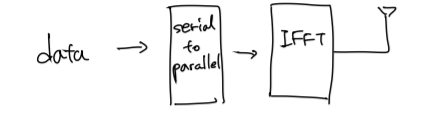
송신단에서의 과정은 위의 그림처럼

수신단에서의 과정은 위의 그림처럼 될 것입니다.
하지만 실제로는 ISI를 없애고, noise의 영향을 최대한 덜 받기 위한 여러가지 기법들을 추가해서 사용하고, 이를 다음 글에서 설명할 예정입니다.
결론
이번 글에서는 OFDM에 대한 기본적인 내용을 다뤄봤습니다.
다음 글에서는 ISI와 ICI를 없애는 기법들을 소개하며 실제로 어떤 방식으로 OFDM이 동작하나 알아보고 오랫동안 작성했던 이 시리즈를 마무리하겠습니다.
Reference
- Fundamentals of Communication Systems, John G Proakis