kipa00's profile image

kipa00

November 21, 2021 19:30

제가 최근에 작업을 하면서 큰 문자열에서 다른 작은 문자열을 많이 찾을 필요가 있었습니다. 정확히는, 이런 일을 해야 할 필요가 있었습니다.

• 문자열 $T$가 주어집니다.
• 문자열 $S_{1}$, $S_{2}$, $\cdots$, $S_{K}$가 $T$에서 등장하는 횟수를 구해야 합니다.
• 모든 정수 $1 \leq i < K$에 대해, $S_{1}$, $S_{2}$, $\cdots$, $S_{i}$에 대한 답을 구한 이후에야 $S_{i+1}$을 알 수 있습니다.
  • 이 조건은 실제 문제 상황보다는 조금 빡빡한 제한이지만, 이렇게 가정해도 큰 무리는 없습니다.

이 상황이 다른 일반적인 상황과 크게 다른 점은 이렇습니다.

• $\log_{10} |T| \approx 8\text{ or }9$ 정도입니다. 즉, 문자가 수억 개에서 십수억 개 정도 됩니다.
• $K \approx 10^{7}$ 정도이고, $\sum_{i} |S_{i}|$ 역시 수억 정도 됩니다. 즉 구해야 하는 대부분의 문자열의 길이가 그렇게 짧지도 않고, 가끔씩 매우 긴 문자열이 들어올 때도 있습니다.

실제로는 $S$를 $100$개 정도씩 묶어서 처리할 수 있지만, $K$가 일반적으로 너무 컸기 때문에 online으로 구하는 것과 큰 차이는 없다고 판단했습니다.

생각할 수 있는 알고리즘

Suffix Array는 사실 다른 선형 시간 알고리즘보다 굉장히 느리게 돌아가는 알고리즘이었기 때문에, 다른 대안부터 고려하기 시작했습니다.

KMP

KMP는 단일 문자열을 찾는 데에는 최고의 알고리즘입니다. 수행 시간은 $\mathcal{O}(|T| + |S|)$이고 locality도 훌륭하기 때문에 매우 빠르게 동작합니다. 이 알고리즘은 대강 다음과 같이 동작합니다.

1. 문자열 $S$를 전처리한다. ($\mathcal{O}(|S|)$ 시간)
2. 문자열 $T$를 훑으면서, 문자열 $S$를 찾는다. ($\mathcal{O}(|T| + |S|)$ 시간)

1번 과정의 수행 시간의 합은 $\sum_{i} |S_{i}|$에 비례하기 때문에 큰 문제는 없습니다. 이 시간이 곧 입력을 읽어들이는 시간이고, 입력도 다 읽지 않고 문자열을 찾겠다는 것은 어불성설이니까요. 문제는 2번 과정의 수행 시간의 합이 $K|T| + \sum_{i} |S_{i}|$에 비례한다는 것입니다. 기준 문자열인 $T$를 매번 읽지 않는 방법이 필요합니다.

Aho-Corasick

이 방법을 개선해서 만든 알고리즘이 Aho-Corasick입니다. 수행 시간은 $\mathcal{O}(|T| + \sum_{i}|S_{i}|)$입니다. $S$들에 대한 locality가 훌륭하지는 않지만 $T$에 대한 locality는 여전히 훌륭합니다. 대강 다음과 같이 동작합니다.

1. 문자열 $S$들을 전처리한다. ($\mathcal{O}(\sum_{i}|S_{i}|)$ 시간)
2. 문자열 $T$를 훑으면서, 각 문자열 $S$를 찾는다. ($\mathcal{O}(|T| + \max_{i} |S_{i}|)$ 시간)

이 알고리즘의 큰 문제는 실제로 답을 구하기 시작하는 2번 과정 이전에 모든 문자열을 들고 1번 과정의 전처리를 해야 하기 때문에, 우리 문제 상황에서는 시행하기 어렵다는 것입니다.

KMP와 Aho-Corasick에 대한 구체적인 설명은 이 글에서 확인할 수 있습니다.

Suffix Array

Suffix Array는 문자열의 모든 접미사를 사전순 정렬한 배열입니다. 문자열이 주어지면, 접미사는 문자열의 시작 위치만으로 완전히 나타낼 수 있습니다. 따라서 아래 표의 오른쪽처럼 문자열을 모두 저장해서 $\mathcal{O}(|T|^{2})$의 공간을 쓰기보다는, 왼쪽처럼 시작 위치만 저장해서 $\mathcal{O}(|T|)$의 공간을 사용할 수 있습니다. 아래 표는 $T$가 abacaba일 때의 Suffix Array입니다.

$k$	$j_{k}$	$T[j_{k}\dots]$
$0$	$6$	a
$1$	$4$	aba
$2$	$0$	abacaba
$3$	$2$	acaba
$4$	$5$	ba
$5$	$1$	bacaba
$6$	$3$	caba

우리의 목표 역시 왼쪽의 수열을 구하는 것입니다. 이 수열이 있을 때, 우리 문제 상황을 어떻게 해결할 수 있는지 생각해 봅시다.

문제 상황을 조금 다르게 생각하면, 모든 $i$에 대해 $T[j\dots{j+|S_{i}|}] = S_{i}$인 $j$의 개수를 구하라는 것입니다. 중간의 등식은 $T[j\dots]$가 $S_{i}$로 시작한다는 말과 동치이므로,

모든 $i$에 대해, $T[j\dots]$가 $S_{i}$로 시작하는 $j$의 개수를 구하라.

가 됩니다. 만일 접미사 $T[j\dots]$가 사전순 정렬되어 있다면, 이 접미사들이 $S_{i}$로 시작하는 위치는 구간이 될 것입니다.

예를 들어 $S_{1}$이 ab라 합시다. 각 접미사가 첫 번째 글자만 보아도 정렬되어 있다는 사실을 생각합시다. 처음에 찾고자 하는 구간을 전체 구간으로 잡고, 이분 탐색을 시행해서 a로 시작하는 구간을 전부 찾습니다. 표에서는 $[0, 4)$ 구간이 됩니다. 이 구간 안에서는 두 번째 글자들이 모두 정렬되어 있습니다! 그러면, 이번에는 두 번째 글자를 기준으로 이분 탐색을 시행할 수 있습니다. 이런 식으로 그 다음 글자가 정렬되어 있음을 이용해서 마지막 문자까지 반복하면 됩니다.

최종 답은 마지막 문자까지 구간을 줄여 가며 전부 찾았을 때 $[s, e)$ 구간이 나왔다면, $(e - s)$가 됩니다. 여기에서는 $[1, 3)$ 구간이 최종 구간이므로 ab는 $2$번 등장했음을 알 수 있습니다.

이런 식으로 시행한다면, Suffix Array가 주어진다면, 각 문자열에 대해 $|S_{i}| \log |T|$ 정도의 시간에 개수를 구할 수 있으므로, 시간 복잡도가 $\mathcal{O}\left(\left(\sum_{i}|S_{i}|\right) \log |T|\right)$ 정도가 됩니다. 이 정도면 아주 훌륭한 시간복잡도입니다!

그러면 우리에게는 이런 질문이 남습니다.

Suffix Array는 얼마나 빨리 구할 수 있죠?

이 단락에서는 더 이상 $S_{i}$를 생각할 필요가 없기 때문에 $S_{i}$에 대한 논의는 잊어버리고, $|T| =: n$이라 두겠습니다.

경쟁적 프로그래밍(CP)과 문제 풀이(PS)에 익숙하시다면, Suffix Array를 구하는 $\mathcal{O}(n \log^{2} n)$과 $\mathcal{O}(n \log n)$ 알고리즘을 잘 알고 계실 것입니다. 이 알고리즘족에 대한 설명은 이 글이 굉장히 잘 설명하고 있습니다. 이 글에서 소개하는 구체적인 알고리즘과 여기서 소개할 알고리즘은 거리가 상당히 멀지만, 속도를 더 높이기 위한 technique들을 링크한 글에서 잘 설명하고 있으므로 이 알고리즘을 전혀 모르신다면 숙독하고 오시는 것을 권장합니다. 링크한 글에서는 LCP Array를 구성하는 선형 시간 알고리즘인 Kasai’s algorithm까지 같이 다루고 있으나 이 글에서는 필요하지 않습니다.

한편, 이런 알고리즘이 나오기 전부터 이미 Suffix Array를 구하는 $\mathcal{O}(n)$ 알고리즘이 매우 잘 알려져 있었는데, 이것은 Suffix Tree를 구성하고 이것을 DFS로 preorder 순회해서 시작 위치를 뽑아내는 방법입니다. (링크의 글은 관심이 생긴다면 읽어보시면 되고, 이 글의 주제와 크게 관련은 없습니다.) 35페이지라는 방대한 분량이 시사하듯, 이 알고리즘은 매우 복잡하며, 수행 시간(흔히 말하는 “상수”)도 그렇게 빠르지는 않은 방법입니다.

우리의 목표는, 글의 제목이 시사하듯이, Suffix Array를 명시적인 Suffix Tree의 구성 없이 선형 시간에 구하는 것입니다.

Skew Algorithm ($2/3$-SA)

먼저 소개할 알고리즘은 Skew Algorithm [1] 입니다. 이 방법은 Suffix Tree를 만드는 방법 중 두 Suffix Tree를 합쳐서 더 큰 Suffix Tree를 만드는 방법 [2] 에서, 어마어마한 수정을 가해 Suffix Tree를 모두 없앤 방법입니다. 이 알고리즘은 문제풀이를 하는 사람들 사이에서도 아는 사람들은 아는 것 같습니다. $2/3$-SA는 뒤에 소개할 알고리즘과의 비교를 위해 제가 임의로 붙인 이름입니다.

다음과 같은 과정으로 동작합니다.

1. Triplet을 정렬한다.
2. Triplet으로 새 문자열을 구성한 후, 이것을 재귀 호출한다. (재귀 호출하는 문자열의 길이는 기존 문자열의 $2/3$ 정도.)
3. (전체 문자열의 $2/3$에 해당하는 접미사의 순서를 알게 된다.) 나머지 $1/3$에 해당하는 접미사를 정렬한다.
4. 2번 과정에서 구한 정렬된 접미사의 $2/3$와 3번 과정에서 구한 나머지 $1/3$을 합쳐 Suffix Array를 완성한다.

Triplet 정렬

문자열에서의 Triplet $T_{j}$를 문자열 내의 위치 $j$에서 뒤로 세 글자까지의 substring으로 정의합니다. 문자가 없으면 모든 문자보다 작은 가상의 문자 $를 삽입해서 생각합니다. 예를 들어 $T$가 abacaba인 경우 Triplet을 정렬된 순서로 나타내면 다음과 같습니다.

$k$	$j_{k}$	$T_{j_{k}}$
$0$	$6$	a$$
$1$	$0$	aba
$2$	$4$	aba
$3$	$2$	aca
$4$	$5$	ba$
$5$	$1$	bac
$6$	$3$	cab

이 과정은 Counting Sort를 활용하여 $\mathcal{O}(n)$에 시행할 수 있습니다. 이것이 실제로 $\mathcal{O}(n)$이 되는 이유는 조금 더 복잡한데, 시간복잡도 분석을 하면서 짚고 넘어가겠습니다. 그러면 이 정렬된 배열에서 인접한 Triplet을 비교해서 각 Triplet이 몇 번째인지를 알 수 있습니다. $0$번 문자를 2번 과정에서 특수한 목적으로 사용할 것이기에, 순서는 $1$번부터 세겠습니다.

$k$	$j_{k}$	$T_{j_{k}}$	순서
$0$	$6$	a$$	$1$
$1$	$0$	aba	$2$
$2$	$4$	aba	$2$
$3$	$2$	aca	$3$
$4$	$5$	ba$	$4$
$5$	$1$	bac	$5$
$6$	$3$	cab	$6$

이것을 구한 뒤에 다시 $j$들을 기준으로 배열을 바꿉니다. 이 과정까지 시행하고 나면, 알고리즘을 진행하는 데는 $T_{j_{k}}$를 잊어버려도 상관없습니다.

$j$	$T_{j}$	순서
$0$	aba	$2$
$1$	bac	$5$
$2$	aca	$3$
$3$	cab	$6$
$4$	aba	$2$
$5$	ba$	$4$
$6$	a$$	$1$

새 문자열 구성 후 재귀 호출

새 문자열 $T_{\text{new}} = T_{0}T_{3}T_{6}\cdots 0 T_{1}T_{4}T_{7} \cdots$와 같이 구성합니다. 이 문자열에 대해 Suffix Array를 구할 수 있습니다.

• 문자열의 크기가 충분히 작아진 경우 기존에 알려진 $\mathcal{O}(n \log^{2} n)$이나 $\mathcal{O}(n \log n)$ 알고리즘을 돌리거나,
• $n \geq 6$인 경우는 재귀 호출을 통해 구할 수 있습니다.

위 예제에서는 $T_{\text{new}}$가 261052가 될 것이고, 이에 대해 Suffix Array를 그리면 다음과 같습니다.

$k$	$\jmath_{k}$	$T_{\text{new}}[\jmath_{k}\dots]$
$0$	$3$	052
$1$	$2$	1052
$2$	$5$	2
$3$	$0$	261052
$4$	$4$	52
$5$	$1$	61052

그런데 이 과정에서 우리가 뭘 구한 걸까요? 수들을 다시 원래의 triplet으로 대체해 봅시다. $0$은 기존에 정의되지 않았고 모든 문자보다 앞서므로 $$$으로 대체하겠습니다.

$k$	$\jmath_{k}$	$T_{\text{new}}[\jmath_{k}\dots]$	Triplet을 원래대로
$0$	$3$	052	$$$bacaba
$1$	$2$	1052	a$$$$$bacaba
$2$	$5$	2	aba
$3$	$0$	261052	abacaba$$$$$bacaba
$4$	$4$	52	bacaba
$5$	$1$	61052	caba$$$$$bacaba

그리고 원래 문자열 $T_{\text{new}}$은 abacaba$$$$$bacaba가 됩니다! 이 문자열의 세 번째 위치마다의 접미사를 순서대로 정렬한 것입니다.

그런데 $T_{0}T_{3}T_{6} \cdots$ 이런 식이라면 세 번째 위치는 원래 위치의 $0$, $3$, $6$ 등 $3$의 배수 위치이고, $T_{1}T_{4}T_{7} \cdots$ 이런 식이라면 세 번째 위치는 원래 위치의 $1$, $4$, $7$ 등 $3$의 배수에 $1$을 더한 것 위치겠죠. 그러므로, 이 정보를 가지고 이들 위치만 정렬한 Suffix Array의 부분수열을 구할 수 있습니다! 이때 새로 구한 Suffix Array의 맨 앞은 항상 $$$로 시작할 것이므로 무시해도 좋습니다.

$k$	$\jmath_{k}$	$j_{k}$	$T[j_{k}\dots]$
$0$	$3$	N/A	N/A
$1$	$2$	$6$	a
$2$	$5$	$4$	aba
$3$	$0$	$0$	abacaba
$4$	$4$	$1$	bacaba
$5$	$1$	$3$	caba

주목해야 할 점이 몇 가지 있습니다:

• 세 번째 열인 $j_{k}$를 보면, 맨 위에서 계산한 Suffix Array $[6, 4, 0, 2, 5, 1, 3]$의 부분수열임을 알 수 있습니다. 이는 네 번째 열인 $T[j_{k}\dots]$가 [작은 문자열의 경우인 $T_{\text{new}}[\jmath_{k}\dots]$에서의 triplet을 원래대로 돌린 문자열]의 접두사가 되기 때문입니다. 이것이 모두 맞아떨어지도록 triplet과 $T_{\text{new}}$를 설계한 것입니다.
• $Z := \lfloor(n + 2)/3\rfloor + 1$ (즉 $Z$는 0이 나타난 위치 바로 다음 위치)라 할 때, $j_{k}$는 다음과 같은 식으로 구해집니다.\[j_{k} = \left\{\begin{array}{cr}3\jmath_{k}&\text{if }\jmath_{k} < Z\\3(\jmath_{k} - Z) + 1&\text{otherwise}\end{array}\right.\]즉, $\jmath_{k}$로부터 $j_{k}$를 계산할 때, $T_{j}$, 심지어 $T_{\text{new}}$의 정보도 전혀 필요하지 않습니다. 앞서 $T_{j}$의 정보를 잊어버려도 된다고 했을 때 정말로 완전히 잊어버려도 된다고 얘기한 것이었습니다. 1번 과정 이후에서 이 메모리 공간을 다른 유익한 공간으로 사용할 수 있습니다.

나머지 접미사를 해당 접미사들끼리 정렬

정렬이 필요한 접미사는 $2$, $5$, $8$ 등 $3$의 배수에 $2$를 더한 것들입니다. 이 접미사들은 이렇게 비교할 수 있습니다.

• 만일 $T[a]$와 $T[b]$가 다르면, 첫 번째 글자가 작은 것이 더 앞에 옵니다.
• 만일 첫 번째 글자가 같으면, $T[a+1\dots]$와 $T[b+1\dots]$의 크기를 비교해야 하며, 이것은 2번 과정에서 이미 계산되어 있기 때문에 빠르게 계산할 수 있습니다.

두 번째 경우를 빠르게 계산하기 위해 먼저 $2/3$-rank $R_{j}$를 구해 놓습니다. $2/3$-rank는 단순히 2번 과정에서 계산한 전체의 $2/3$에 해당하는 접미사에 대해, 그 위치의 접미사가 몇 번째인지를 계산한 것입니다.

$j$	$R_{j}$
$0$	$2$
$1$	$3$
$2$	N/A
$3$	$4$
$4$	$1$
$5$	N/A
$6$	$0$

그러면 $R_{j}$가 정의되지 않은 각 위치를, 위의 아이디어를 사용해서 pair로 나타낼 수 있습니다. 본질적으로는 다르지만, 이 값 역시 그냥 $R_{j}$라고 부르겠습니다.

$j$	$R_{j}$
$0$	$2$
$1$	$3$
$2$	(a, $4$)
$3$	$4$
$4$	$1$
$5$	(b, $0$)
$6$	$0$

이렇게 정렬하고 나면 이 pair 역시 Counting Sort를 통해 $\mathcal{O}(n)$에 정렬할 수 있습니다. 이렇게 하면 우리에게는 두 개의 정렬된 배열 $S_{2/3} = [6, 4, 0, 1, 3]$과 $S_{1/3} = [2, 5]$가 생깁니다. 이 두 개의 배열을 합치기만 하면 Suffix Array가 만들어집니다.

두 정렬된 부분 접미사 배열을 병합

두 배열이 각 배열 안에서는 모두 정렬되어 있기 때문에 Merge Sort의 병합 아이디어를 사용합니다. Wikipedia commons의 animation이 정말 잘 되어 있어서 가져와서 병합 부분만 잘랐습니다. 만일 이 아이디어를 전혀 모르신다면, 이 animation을 한 번쯤 볼 만한 가치가 있습니다.

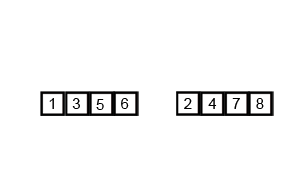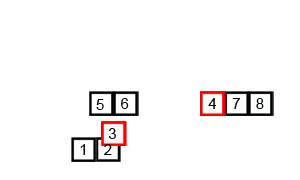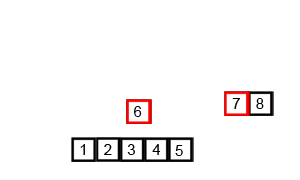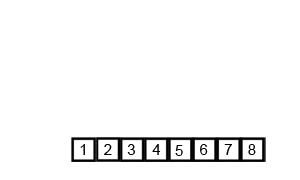
이제 문제는 두 배열에서 뽑은 원소를 어떻게 비교할 것인가입니다. $S_{2/3}$에서 뽑은 원소를 $a$, $S_{1/3}$에서 뽑은 원소를 $b$라 합시다.

1. $T[a]$와 $T[b]$가 다르다면 비교가 끝났습니다. 둘 중 작은 쪽을 먼저 집어넣습니다.
2. $a$가 $3$으로 나누어떨어진다면, $R_{a+1}$과 $R_{b+1}$을 비교하고 비교를 끝냅니다. 비교가 되었다면, 둘 중 작은 쪽을 먼저 집어넣습니다.
3. $T[a+1]$과 $T[b+1]$이 다르다면 비교가 끝났습니다. 둘 중 작은 쪽을 먼저 집어넣습니다.
4. $R_{a+2}$와 $R_{b+2}$를 비교하고 비교를 끝냅니다. 둘 중 작은 쪽을 먼저 집어넣습니다.

이렇게만 적으면 “??? 이게 왜 돼?“가 첫 감상일 것입니다.

core idea는, 증가 횟수 $\iota$를 초기에 $0$으로 두고 $1$씩 늘려 가면서, [$R$ 배열에 정수 값이 있다면 비교하고 종료하고, 실제 문자열인 $T$의 각 인덱스를 비교하고 종료하는] 과정의 반복을 매우 최적화해 적은 것입니다. 이렇게 비교하면, $a$와 $b$는 나머지가 다르기 때문에 $\iota$가 $3$이 되기 전에 비교 과정이 종료합니다. 불필요한 부분을 모두 넣어서 다시 쓰면 다음과 같습니다.

1. $\iota = 0$이고, $R_{a}$와 $R_{b}$에 모두 정수 값이 존재한다면, 이 둘을 비교하고 비교를 끝냅니다. $b$가 $3$으로 나눴을 때 $2$이므로 $R_{b}$가 존재할 리가 없으며 따라서 삭제되었습니다.
2. $\iota = 0$이고, $T[a]$와 $T[b]$가 다르다면 비교를 끝냅니다. 위 비교 과정의 1번 단계입니다.
3. $\iota = 1$이고, $R_{a+\iota}$와 $R_{b+\iota}$에 모두 정수 값이 존재한다면, 이 둘을 비교하고 비교를 끝냅니다.
   • $R_{a+\iota}$와 $R_{b+\iota}$에 대한 상기 조건은 $(a + \iota)$가 $3$으로 나눈 나머지가 $2$가 아니고, $(b + \iota)$가 $3$으로 나눈 나머지가 $2$가 아니라는 것입니다.
   • $b$는 $3$으로 나눈 나머지가 $2$이므로 $b + \iota$는 $3$으로 나눈 나머지가 $0$입니다. 따라서 최적화된 조건은 “$(a + \iota)$를 $3$으로 나눈 나머지가 $2$가 아니다”입니다.
   • $\iota = 1$이므로 “조건은 $a$를 $3$으로 나눈 나머지가 $1$이 아니다”입니다.
   • $a$는 나머지가 $0$ 혹은 $1$이므로, 조건은 “$a$가 $3$으로 나누어떨어진다”입니다. 조건을 최적화한 것이 위 비교 과정의 2번 단계입니다.
4. $\iota = 1$이고, $T[a+\iota]$와 $T[b+\iota]$가 다르다면 비교를 끝냅니다. 위 비교 과정의 3번 단계입니다.
5. $\iota = 2$이고, $R_{a+\iota}$와 $R_{b+\iota}$에 모두 정수 값이 존재한다면, 이 둘을 비교하고 비교를 끝냅니다.
   • 앞선 단계에서 $a$를 $3$으로 나눈 나머지가 $0$인 경우는 처리되었으므로 $a$를 $3$으로 나눈 나머지는 $1$입니다. $b$를 $3$으로 나눈 나머지는 $2$입니다.
   • $R_{a+\iota}$와 $R_{b+\iota}$에 대한 상기 조건은 $(a + \iota)$가 $3$으로 나눈 나머지가 $2$가 아니고, $(b + \iota)$가 $3$으로 나눈 나머지가 $2$가 아니라는 것입니다.
   • $(a+\iota)$를 $3$으로 나눈 나머지는 $0$이고, $(b+\iota)$를 $3$으로 나눈 나머지는 $1$입니다.
   • 따라서 무조건 시행할 수 있습니다. 조건을 없앤 것이 위 비교 과정의 4번 단계입니다.
6. $\iota = 2$이고, $T[a+\iota]$와 $T[b+\iota]$가 다르다면 비교를 끝냅니다. 이 과정에 올 일이 없으므로, 이 과정과 이후 과정이 모두 삭제되었습니다.

비교가 조금 복잡하지만, 이미 있던 배열만 참조해서 비교하므로 상수 시간에 비교를 시행할 수 있고, 따라서 전체 병합을 $\mathcal{O}(n)$에 시행할 수 있습니다.

시간 복잡도 분석

시간 복잡도는 재귀 호출을 제외하고 대체로 선형 시간 안에 동작함을 이미 확인하셨을 것입니다. 1번 과정과 3번 과정에서 의심스러운 부분은 문자를 기준으로 Counting Sort를 시행하는 부분입니다.

이를 해결하기 위해 $|\Sigma|$를 의도적으로 $n$ 이하로 떨어뜨릴 수 있습니다. 최초에 Counting Sort를 한 번 시행한 후 문자를 상대적인 순서를 유지하며 $n$ 이하로 바꿀 수 있기 때문입니다. 이렇게 하는 데에 시간복잡도는 비교 정렬을 이용하면 $\mathcal{O}(n \log n)$ (그러나 $n \log n$은 정렬에만 소모되는 시간이기 때문에 locality가 좋은 수많은 방법을 사용할 수 있고 굉장히 빠름) 혹은 문자의 개수가 적은 경우 Counting Sort를 여기에도 활용하면 $\mathcal{O}(n + |\Sigma|)$입니다. 이렇게 전처리할 수 있으므로 본 알고리즘에서는 $|\Sigma| \leq \frac{3}{2}n + \mathcal{O}(1)$을 가정합니다.

이 technique에도 불구하고 $|\Sigma|$를 크게 잡는 이유는, 2번 과정에서 $|\Sigma_{\text{new}}| = n$을 사용해서 $|T_{\text{new}}| = \frac{2}{3}n + \mathcal{O}(1)$인 문자열을 만들고 이를 재귀함수에 넣기 때문입니다. 즉, 재귀 호출된 함수의 입장에선 $|T_{\text{new}}| = n$인 문자열의 문자 집합이 $|\Sigma| = \frac{3}{2}n + \mathcal{O}(1)$인 상황입니다.

어쨌든, 전체 과정은 $T(n) = \mathcal{O}(n) + T\left(\frac{2}{3} n\right)$이 됩니다. 시간 복잡도는 $T(n) = \mathcal{O}(n)$입니다.

SA-IS ($1/2$-SA)

SA-IS는 Ko와 Aluru의 Suffix Array 알고리즘 [3] 을 Nong et al. [4] 이 Induced Sorting idea로 더 빠르게 확장한 것입니다. 이름의 SA는 Suffix Array이고, IS는 Induced Sorting입니다. $1/2$-SA라는 이름은 역시 비교를 위해 제가 임의로 붙인 이름입니다.

별도로 알아야 할 것이 없어서 알고리즘을 쭉 훑기만 하고 단순하게 지나갔던 Skew Algorithm과는 달리, SA-IS는 새로 정의할 용어가 좀 있습니다.

Suffix Type

각 접미사 $j$가 작다 혹은 크다라는 것을 다음과 같이 정의합니다.

• 작다: $T[j\dots]$가 $T[j+1\dots]$보다 작다.
• 크다: $T[j\dots]$가 $T[j+1\dots]$보다 크다.

원문인 [3]에서는 Small과 Large의 앞 글자를 따서 S-type과 L-type이라고 부릅니다. 짚고 넘어가야 하는 점이 몇 가지 있습니다.

• 모든 접미사는 작거나 큽니다. $T[j\dots]$는 $T[j+1\dots]$보다 크거나 작거나 같은데, 두 문자열은 길이가 다르므로 같을 수 없습니다. 따라서 둘을 비교하면 한쪽이 클 수밖에 없습니다.
• 만일 $T[j]$와 $T[j+1]$이 다르다면 접미사 $j$가 큰지 작은지를 곧바로 알 수 있습니다. $T[j]$가 크다면 접미사 $j$는 크고, $T[j+1]$이 크다면 접미사 $j$는 작습니다.
• $T[j]$와 $T[j+1]$이 같다면 $T[j\dots]$와 $T[j+1\dots]$를 비교하기 위해 $T[j+1\dots]$와 $T[j+2\dots]$를 비교해서 어느 쪽이 큰지를 확인해야 하는데, 이는 접미사 $(j+1)$이 큰지 작은지의 여부와 일치합니다. 이 성질을 보존성이라고 부르겠습니다.
• 접미사 $(n-1)$은 무조건 큽니다. $T[n\dots]$이 빈 문자열이고, 빈 문자열은 어떤 문자열보다 작기 때문입니다.

벌써 머릿속에서 Suffix Type을 분류하는 선형 시간 알고리즘을 구상하신 분도 있을 것입니다. 다음과 같습니다.

1. 접미사 $(n-1)$은 큽니다.
2. $j$를 $(n-2)$부터 $0$까지 $1$씩 줄여 가며 다음을 반복합니다.
   • $T[j] > T[j+1]$이면 접미사 $j$는 큽니다.
   • $T[j] < T[j+1]$이면 접미사 $j$는 작습니다.
   • $T[j] = T[j+1]$이면 접미사 $j$는 바로 이후 접미사인 접미사 $(j+1)$과 크기(Suffix Type)가 같습니다.

굉장히 중요한 사실 하나가 있는데, 이건 예측하기 어려우셨을지도 모르겠습니다.

정리. 두 접미사 $i$와 $j$에 대해 접미사 $i$가 크고 접미사 $j$가 작으며 $T[i] = T[j]$라면, $T[i\dots] < T[j\dots]$이다.

아이디어: 문자 $c$에 대해 큰 접미사 중 $c$로 시작하는 최대 접미사를 생각하면, $ccccccc\cdots$와 같은 형태가 될 것입니다. 여기서 어떤 위치에 $c$보다 큰 문자가 등장하면 접미사가 작아지고, $c$보다 작은 문자 $d$가 등장해서 $ccccd\cdots$와 같은 접미사가 만들어졌다면 맨 앞에 $c$를 하나 덧붙인 $cccccd\cdots$는 이 접미사보다 크면서 여전히 큰 접미사니까요. 그런데 비슷한 이유로 작은 접미사 중 $c$로 시작하는 최소 접미사는 $ccccccc\cdots$와 같은 형태입니다. 즉, $ccccccc\cdots$를 기준으로 큰 접미사가 앞에, 작은 접미사가 뒤에 오게 됩니다.

증명. 이 단락은 엄밀한 증명입니다. 위 아이디어를 이해했다면, 아래 증명을 읽지 않고 가장 가까운 $\square$를 찾아서 빠져나가셔도 됩니다.

접미사 $i$가 크기 때문에 $T[i]$가 $T[i+1]$보다 작을 수는 없습니다. 만일 그랬다면 첫 글자를 비교해서 $T[i\dots] < T[i+1\dots]$가 되었을 것이므로 접미사 $i$가 작아지기 때문입니다. 비슷한 이유로 접미사 $j$가 작기 때문에 $T[j]$가 $T[j+1]$보다 클 수는 없습니다. 즉 $T[i] \geq T[i+1]$, $T[j] \leq T[j+1]$입니다. 따라서\[T[i+1] \leq T[i] = T[j] \leq T[j+1]\]이므로 $T[i+1]\leq T[j+1]$입니다. 이제 $T[i\dots]$의 길이에 대한 수학적 귀납법을 적용합니다.

• $T[i] \neq T[i+1]$ 혹은 $T[j] \neq T[j+1]$인 경우. 이 경우가 $T[i\dots]$의 길이가 $1$인 경우를 포함하기 때문에 base case라고 할 수 있습니다.
  • $T[i+1] = T[j+1]$이라고 하면, 위 부등호 수식을 다시 쓰면\[T[i+1] \leq T[i] = T[j] \leq T[j+1] = T[i+1]\]이므로 $T[i] = T[i+1] = T[j] = T[j+1]$입니다. 이것은 가정에 모순이므로, $T[i+1] \neq T[j+1]$이며 따라서 $T[i+1] < T[j+1]$입니다.
  • 이제 $T[i\dots]$와 $T[j\dots]$를 비교해 봅시다. $T[i] = T[j]$이므로 다음 문자를 비교하면, $T[i+1] < T[j+1]$이므로 여기서 비교가 끝나며, $T[i\dots] < T[j\dots]$라는 결론이 얻어집니다.
• $T[i] = T[i+1]$이고 $T[j] = T[j+1]$인 경우. 수학적 귀납법을 적용합니다.
  • $T[i] = T[i+1]$이므로 보존성에 의해 접미사 $(i+1)$는 크며, 마찬가지로 $T[j] = T[j+1]$이므로 접미사 $(j+1)$은 작습니다. 또한\[T[i+1] = T[i] = T[j] = T[j+1]\]입니다. 마지막으로 $T[i+1\dots]$는 $T[i\dots]$보다 길이가 더 작으므로, $(i+1)$과 $(j+1)$에 대해 귀납 가정을 적용할 수 있는 모든 조건이 만족됩니다. 여기서 얻을 수 있는 결론은 $T[i+1\dots] < T[j+1\dots]$입니다.
  • 이제 $T[i\dots]$와 $T[j\dots]$를 비교해 봅시다. $T[i] = T[j]$이므로 이 둘을 비교하는 것은 $T[i+1\dots]$와 $T[j+1\dots]$를 비교하는 것과 같습니다. 그런데 위 귀납 결론에 의해 $T[i+1\dots] < T[j+1\dots]$이므로, $T[i\dots] < T[j\dots]$라는 결론이 얻어집니다.

$\square$

정리가 말해주는 것은 아래 그림과 같이, 완성된 SA에서 시작 글자가 같은 접미사들끼리 모으면 항상 큰 접미사가 작은 접미사보다 앞에 온다는 뜻입니다.

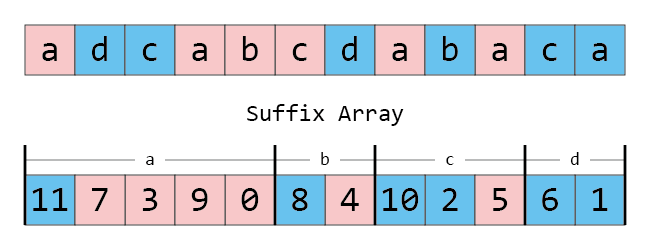
즉, 큰 접미사와 작은 접미사를 각각 정렬할 수 있으면, 전체를 합치는 것은 이제 아무 문제가 없습니다! 정렬된 각 접미사를 첫 번째 문자를 기준으로 모은 다음, 첫 번째 문자가 같은 배열 안에선 큰 접미사를 작은 접미사 앞에 놓으면 되기 때문입니다.

Induced Sorting

이 단락이 Ko and Aluru가 밝혀낸 부분입니다. 구체적인 정의와 엄밀한 증명이 필요하시면 [3]을 참조하세요.

그런데 만일 큰 접미사만 정렬되어 있는 경우, 작은 접미사를 이를 이용해서 정렬할 수 있을 것 같습니다. 왜냐하면 어쨌든 모든 작은 접미사 뒤엔 언젠가는 큰 접미사가 뒤따라오니까요! (접미사 $(n-1)$이 큰 접미사라는 사실을 기억하시나요?) Induced Sorting이라는 말은 이렇게, 이미 정렬된 큰 접미사에서부터 정렬 순서를 유도해 작은 접미사를 정렬하겠다는 뜻입니다.

이제 반대로도 발상해 봅시다. 작은 접미사만 정렬되어 있는 경우, 큰 접미사를 이를 이용해서 정렬할 수 있을까요? 우선 모든 큰 접미사 뒤에 작은 접미사가 뒤따라오지 않는다는 점이 약간 문제가 될 수 있으므로, 가상의 접미사인 접미사 $n$을 작은 접미사로 정의합니다. 정의 확장의 관점에서는 오히려 큰 접미사로 정의하는 것이 자연스러우나 접미사 $n$을 실제로 사용할 것은 아니므로 원하는 대로 정의해 줄 수 있습니다.

먼저 작은 접미사를 이용해서 큰 접미사를 정렬하는 것부터 해 봅시다. 큰 접미사를 쭉 뽑으면 그림의 가로 행과 같이 스택이 여럿 있고, 가장 높은 위치의 stack부터 뽑아서 정렬하는 multi-way merge가 됩니다.

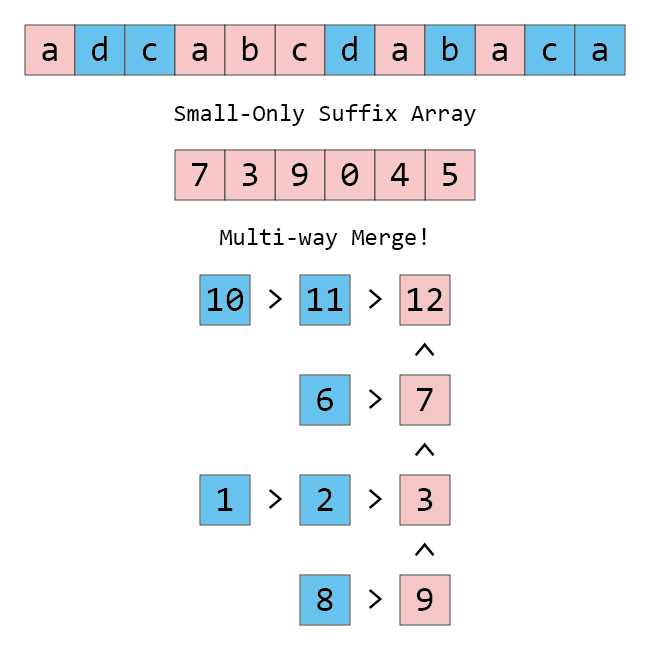
그러면 맨 위에 있는 스택의 맨 위 값을 순서대로 빼서 정렬하면 작은 접미사를 모두 정렬할 수 있는 건 알겠는데, 빼고 남은 스택을 새로 넣을 때 어디에 넣어야 할까요? 다음과 같이 넣으면 됩니다.

• 스택을 맨 위 접미사의 (a) 첫 글자 순서로 나누면 자연스레 정렬이 됩니다.
• 맨 위 접미사의 첫 글자가 같은 스택끼리는, 새로 삽입되는 위치는 (b) 모든 작은 접미사 앞, 그리고 (c) 모든 큰 접미사 뒤입니다.

(a)와 (b)는 정리 덕분에 당연한 얘기이고, 실제로 효과도 있을 거 같습니다. 그런데 (c)는 왜일까요?

주장. 기준 (c)는 올바릅니다.

아이디어. 지금 스택에서 막 접미사 $p$가 빠졌다고 해 봅시다. 그러면 현재 스택의 맨 위에 있는 비교 대상이 되는 접미사는 접미사 $(p-1)$입니다. 우리가 증명하고 싶은 것은 접미사 $(p-1)$이 첫 글자가 접미사 $(p-1)$과 같은 큰 접미사 $q$보다 크다는 것입니다. 접미사 $q$와 접미사 $(p-1)$의 대소 관계는, 첫 글자가 같으므로 접미사 $(q+1)$과 접미사 $p$의 대소 관계와 같습니다.

그런데 초기 상태에서 모든 스택의 맨 위는 작은 접미사임에도 불구하고 접미사 $q$가 큰 접미사라는 말은, 접미사 $q$ 앞에 이미 접미사 $(q+1)$이 있었고, 이것이 접미사 $p$보다 훨씬 먼저 빠졌다는 얘기입니다. (접미사 $p$는 스택에서 막 빠졌고 접미사 $(q+1)$이 스택에서 빠졌어야 이게 말이 되는 상황이니까요.) 따라서 접미사 $(q+1)$이 $p$보다 작습니다. 그러면 접미사 $q$ 역시 접미사 $(p-1)$보다 작아야 합니다!

증명. 아이디어와 같이 하면 되는데, 위 알고리즘 전체를 고려해 수학적 귀납법을 적용하여, 맨 위의 스택에서 맨 위를 반복해서 빼는 알고리즘을 적용했을 때 “스택에서 막 접미사 $p$를 빼서 정렬된 배열에 넣은 시점”에 배열 전체가 올바른 순서를 가지고 있음을 같이 증명할 필요가 있습니다. 구체적인 증명은 매우 tedious하므로 생략하며, 궁금하신 경우 [3]의 Lemma 2, Corollary 3, Lemma 4 및 그 아래의 알고리즘을 읽어보시면 됩니다.

$\boxtimes$ $\square$

그런데 이 상황에서 어떤 큰 접미사를 스택에서 뺀다면, 빠진 큰 접미사의 구체적인 위치까지 알 수 있습니다. 각 문자의 개수와 큰 접미사/작은 접미사 개수를 세어서 Suffix Array에 구간도 나누고 색칠도 할 수 있기 때문입니다. 정말로, 적절한 필기구가 있다면 안에 들어갈 정수 빼고 다 그릴 수 있습니다.

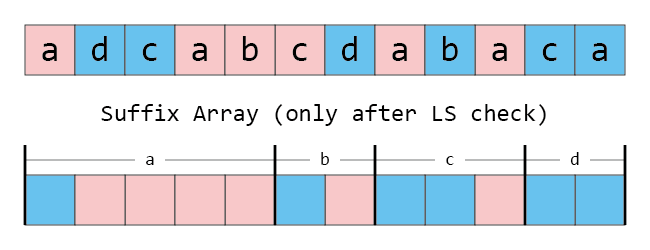
그렇다면, 작은 접미사를 모두 올바른 위치에 넣어 두고 큰 접미사를 저 배열에 곧바로 쓰면 안 될까요? 즉,

1. (일부 혹은 전부가 비어 있을 수 있고, 파란색 자리는 모두 비어 있는) Suffix Array $J$에 대해 $(n-1)$을 $(n-1)$번째 글자와 일치하는 가장 왼쪽의 파란색 자리에 쓴다. (이 과정은 원래 맨 앞에 있는 가상의 접미사 $n$에 대해, $(n-1)$이 큰 접미사이므로 이를 처리하는 과정입니다.)
2. $J$의 모든 원소 $J_{i}$를 순서대로 $i = 0$부터 $i = n-1$까지 보면서
   • 만일 접미사 $(J_{i} - 1)$이 $0$ 이상이며 큰 접미사이면 접미사 $(J_{i} - 1)$의 첫 글자와 일치하는 파란색 자리 중 가장 왼쪽의 비어 있는 자리에 $(J_{i} - 1)$을 쓴다.

를 시행하면, 스택을 명시적으로 관리하지 않고도 똑같은 효과를 누릴 수 있습니다! 현재 보고 있는 $i$ 이후에 적힌 수를 남아 있는 스택들이라고 생각하면, 스택에서 원소 하나를 빼서 쓰는 과정은 이미 처리되었고 ($J_{i}$가 바로 그 자리이니) 다음 스택은 자연스레 위에 표시된 자리에 쓰여야 합니다.

큰 접미사를 이용해서 작은 접미사를 정렬하는 것도 똑같이 해 주면 되는데, 아래 그림에서 보시다시피 스택의 가장 아래가 가장 작기 때문에, 큰 것부터 거꾸로 쓰는 것이 조금 더 자연스럽습니다.

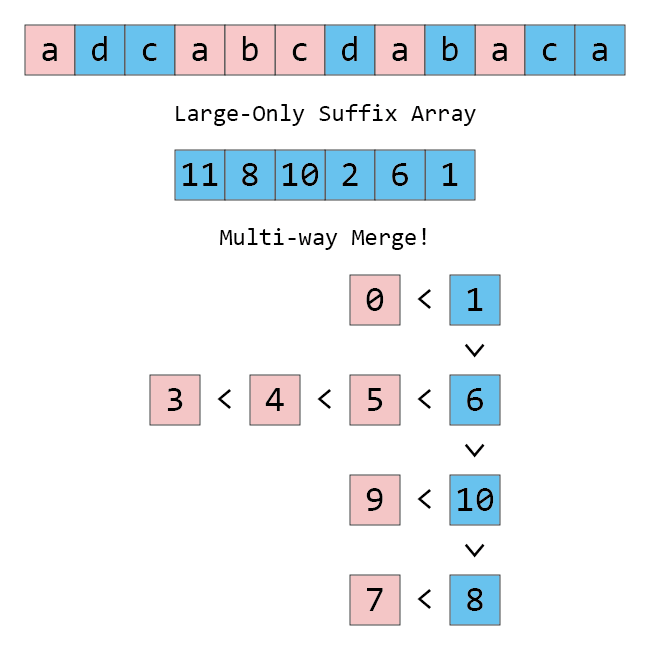
큰 접미사를 작은 접미사 기준으로 정렬한 다음, 정렬된 큰 접미사를 기준으로 작은 접미사를 정렬한다면 알고리즘은 다음과 같습니다. 아래 알고리즘을 IS 알고리즘이라고 부르겠습니다.

1. (일부 혹은 전부가 비어 있을 수 있고, 파란색 자리는 모두 비어 있는) Suffix Array $J$에 대해 $(n-1)$을 $(n-1)$번째 글자와 일치하는 가장 왼쪽의 파란색 자리에 쓴다.
2. $J$의 모든 원소 $J_{i}$를 순서대로 $i = 0$부터 $i = n-1$까지 보면서
   • 만일 접미사 $(J_{i} - 1)$이 $0$ 이상이며 큰 접미사이면 접미사 $(J_{i} - 1)$의 첫 글자와 일치하는 파란색 자리 중 가장 왼쪽의 비어 있는 자리에 $(J_{i} - 1)$을 쓴다.
3. 빨간색 자리를 모두 비운다.
4. $J$의 모든 원소 $J_{i}$를 역순으로 $i = n-1$부터 $i = 0$까지 보면서
   • 만일 접미사 $(J_{i} - 1)$이 $0$ 이상이며 작은 접미사이면 접미사 $(J_{i} - 1)$의 첫 글자와 일치하는 빨간색 자리 중 가장 오른쪽의 비어 있는 자리에 $(J_{i} - 1)$을 쓴다.

위 애니메이션은 이 과정을 보여줍니다. 주의해서 보셔야 할 점이 하나 있습니다.

• 2번 과정에서, 작은 접미사가 앞에 있는 작은 접미사는 무시됩니다.
  • 조건을 만족하지 않기도 하지만, 작은 접미사가 앞에 있는 작은 접미사는 어쨌든 빨간색 자리에 있을 것인데, $J$가 개수가 딱 맞게 색칠되었기 때문에 2번 과정에서 빨간색 자리에 쓰는 일은 없습니다! 따라서 정말로 있으나 마나입니다.
  • 그렇다면 4번 과정에서 작은 접미사를 다시 정렬하니 굳이 정렬 대상에 넣지 않아도 됩니다! 따라서 직전 접미사가 큰 접미사인 작은 접미사들만 정렬하면 됩니다. 이 접미사들을 작아진 접미사라고 부르면 그럴 듯해 보입니다. 앞으로 작아진 접미사에 집중하겠습니다.
  • 위 애니메이션에서도 처음에 작아진 접미사만 정렬된 상태로 들어가 있습니다.

자명하지만 놓치기 쉬운 부분을 설명드리면, 접미사 $0$은 작아진 접미사가 될 수 없습니다. 정의상 “접미사 $(-1)$이 큰 접미사이다”가 맞는 말이 아니기도 하고, 우리가 최초에 작아진 접미사를 정렬하려는 목적이 앞에 있는 큰 접미사를 정렬하기 위함이기 때문에 목적에도 별로 맞지 않습니다.

작아진 접미사의 개수

이 단락은 SA-IS가 평균적인 상황에서 얼마나 더 강력해지는지를 계산하는 부분이므로, 수식이 어마무시하게 많습니다. 최악의 경우만 분석해도 괜찮다면, 다음 문단만 읽고 이 단락을 통째로 넘기셔도 좋습니다.

작아진 접미사는 몇 개 있을까요? 최악의 경우, 큰 접미사 다음에 작은 접미사가 나와야 작은 접미사를 작아진 접미사로 부를 수 있고, 접미사 $(n-1)$이 언제나 큰 접미사이므로 무시하면, 작아진 접미사의 개수는 $(n-1)/2$를 넘을 수 없습니다.

평균적으로 몇 개 있는지는 답하기 조금 어렵습니다. 문자 집합이 $\Sigma = \{0, 1, \cdots, k-1\}$로 총 $k \geq 2$개인 상황에서 $S_{i, j}$를 길이가 $i$이고 첫 문자가 $j$이며 접미사 $0$이 작은 문자열의 개수로 정의하고, $L_{i, j}$를 길이가 $i$이고 첫 문자가 $j$이며 접미사 $0$이 큰 문자열의 개수로 정의합니다. 그러면 $i \geq 2$일 때\begin{align}S_{i, j} &= S_{i-1, j} + \sum_{\jmath = j+1}^{k-1}\left(S_{i-1, \jmath} + L_{i-1, \jmath}\right)\\L_{i, j} &= L_{i-1, j} + \sum_{\jmath = 0}^{j-1}\left(S_{i-1, \jmath} + L_{i-1, \jmath}\right)\end{align}입니다. 일단 이 식을 풀어서 각 접미사가 몇 개 있는지에 대해 답합시다.

$(S_{i, j} + L_{i, j})$가 구하기 쉬운데, 이것이 의미하는 바는 “길이가 $i$이고 첫 문자가 $j$인 문자열의 개수”이므로 $k^{i-1}$입니다. 그러면 위 식은 이렇게 정리됩니다.\begin{align}S_{i, j} &= S_{i-1, j} + (k-j-1)k^{i-2}\\L_{i, j} &= L_{i-1, j} + j \cdot k^{i-2}\end{align}

각각을 $i = 2$까지 계차 대입해서 풀면 다음이 얻어집니다. 다행히도 아래 식들은 $i = 1$에서 모두 잘 성립하므로, $i \geq 1$에서 성립한다고 생각해도 좋을 것입니다.\begin{align}S_{i, j} &= \frac{k-j-1}{k-1}\cdot(k^{i-1} - 1)\\L_{i, j} &= 1 + \frac{j}{k-1}\cdot(k^{i-1} - 1)\end{align}

이제 $\mathcal{S}_{i,j}$를 길이가 $i$이고 첫 문자가 $j$이며 접미사 $0$이 작은 문자열의 작아진 접미사의 개수의 합으로 정의하고, $\mathcal{L}_{i,j}$를 길이가 $i$이고 첫 문자가 $j$이며 접미사 $0$이 큰 문자열의 작아진 접미사의 개수의 합으로 정의합니다. 그러면 $i \geq 2$일 때\begin{align}\mathcal{S}_{i, j} &= \mathcal{S}_{i-1, j} + \sum_{\jmath=j+1}^{k-1}\left(\mathcal{S}_{i-1,\jmath}+\mathcal{L}_{i-1,\jmath}\right)+\sum_{\jmath = j + 1}^{k-1}L_{i-1,\jmath}\\\mathcal{L}_{i,j} &= \mathcal{L}_{i-1,j}+\sum_{\jmath=0}^{j-1}\left(\mathcal{S}_{i-1,\jmath}+\mathcal{L}_{i-1,\jmath}\right)\end{align}입니다.

우리가 필요한 것은 $\mathcal{T}_{i,j} := \mathcal{S}_{i,j} + \mathcal{L}_{i,j}$의 값입니다. 따라서 그냥 두 식을 더하겠습니다.\[\mathcal{T}_{i, j} = \sum_{\jmath=0}^{k-1} \mathcal{T}_{i-1,\jmath} + \sum_{\jmath = j + 1}^{k-1}L_{i-1,\jmath}\]

$L_{i,j}$는 closed form을 알고 있어서 계산할 수 있습니다.\[\mathcal{T}_{i, j} = \sum_{\jmath=0}^{k-1} \mathcal{T}_{i-1,\jmath} + (k - j - 1) + \frac{(k+j)(k-j-1)}{2(k-1)} \cdot (k^{i-2} - 1)\]

식 내에 있는 커다란 시그마가 거슬리는데 이 시그마가 $j$에 의존하지 않으므로, 먼저 $(\mathcal{T}_{i, j} - \mathcal{T}_{i, 0})$를 구하면 식을 정리할 수 있습니다.\[\mathcal{T}_{i, j} - \mathcal{T}_{i, 0} = -j -\frac{j(j+1)}{2(k-1)} (k^{i-2} - 1)\]

\begin{align}\mathcal{T}_{i,0} &= k\mathcal{T}_{i-1, 0} + \sum_{\jmath=0}^{k-1} \left(\mathcal{T}_{i-1,\jmath} - \mathcal{T}_{i-1,0}\right) + (k - 1) + \frac{k}{2} \cdot (k^{i-2} - 1)\\&= k\mathcal{T}_{i-1,0} - \frac{k(k-1)}{2} - \frac{k(k+1)}{6} \cdot (k^{i-3} - 1) + (k - 1) + \frac{k}{2} \cdot (k^{i-2} - 1)\\&= k\mathcal{T}_{i-1,0} + \frac{k^{i-1}}{3} - \frac{k^{i-2}}{6} + \left(-\frac{k^{2}}{3} + \frac{7}{6}k - 1\right)\end{align}

위 전개를 $i - 1 \geq 2$에 대해서 사용했으므로 이 식은 $i \geq 3$이 됩니다. 식 전체를 $k^{i}$으로 나누고 계차 대입해서 풀면 $\mathcal{T}_{i, 0}$에 대한 식을 얻을 수 있습니다. $\mathcal{T}_{2, 0} = k-1$입니다. \begin{align}\frac{\mathcal{T}_{i,0}}{k^{i}} &= \frac{\mathcal{T}_{i-1,0}}{k^{i-1}} + \frac{1}{3k} - \frac{1}{6k^{2}} + \left(-\frac{k^{2}}{3} + \frac{7}{6}k - 1\right)\frac{1}{k^{i}}\\\frac{\mathcal{T}_{i,0}}{k^{i}} &= \frac{1}{k} - \frac{1}{k^{2}} + \sum_{i=3}^{i}\left(\frac{1}{3k} - \frac{1}{6k^{2}} + \left(-\frac{k^{2}}{3} + \frac{7}{6}k - 1\right)\frac{1}{k^{i}}\right)\\&=\left(\frac{i+1}{3k} - \frac{i+4}{6k^{2}}\right) + \left(-\frac{k^{2}}{3} + \frac{7}{6}k - 1\right)\frac{1}{k^{i}} \cdot \frac{k^{i-2} - 1}{k - 1}\end{align}

최종적으로 구하고자 하는 길이 $i$인 문자열에서의 작아진 접미사의 개수의 합은\[\sum_{\jmath=0}^{k-1} \mathcal{T}_{i,\jmath} = \mathcal{T}_{i+1,0} - (k-1) - \frac{k}{2} \cdot (k^{i-1} - 1)\]입니다. 이 값을 구체적으로 계산할 수 있겠지만 합 자체는 너무 크기도 하니, $k^{i}$로 나누어 평균으로 만들고 $i$로 한 번 더 나누어 길이에 대한 비율을 구해 봅시다.

\begin{align}\lim_{i\rightarrow \infty}\frac{1}{ik^{i}}\sum_{\jmath=0}^{k-1}\mathcal{T}_{i,\jmath} &= \lim_{i \rightarrow \infty}\frac{1}{ik^{i}} \left(\mathcal{T}_{i+1,0} - (k-1) - \frac{k}{2} \cdot (k^{i-1} - 1)\right)\\&=\lim_{i \rightarrow \infty}\frac{1}{ik^{i}} \mathcal{T}_{i+1,0}\\&=\lim_{i \rightarrow \infty}\frac{k}{i} \left(\left(\frac{i+2}{3k} - \frac{i+5}{6k^{2}}\right) + \left(-\frac{k^{2}}{3} + \frac{7}{6}k - 1\right)\frac{1}{k^{i+1}} \cdot \frac{k^{i-1} - 1}{k - 1}\right)\\&= \frac{1}{3} - \frac{1}{6k}.\end{align}

즉, 예를 들어 A, C, G, T로만 이루어진 염기 서열을 다룰 때는 작아진 접미사의 비율이 $\frac{7}{24}$ 정도로 수렴하고, 그렇지 않고 $k$가 매우 큰 일반적인 상황에서도 평균 비율이 $\frac{1}{3}$을 넘지 않습니다. $k \geq 2$인 경우부터 이 식이 의미를 가지므로 평균 비율의 하한은 $\frac{1}{4}$입니다.

Induced Sorting, Again!

이 단락이 Nong et al.이 밝혀낸 부분입니다. 구체적인 정의와 엄밀한 증명이 필요하시면 [4]를 참조하세요.

$J$가 굳이 정렬되어 있지 않아도 IS 알고리즘을 시행할 수는 있습니다. 시행하면 어떻게 될까요? 즉, 빨간색 자리에 작은 접미사들을 첫 글자를 만족하게 아무 순서로 넣고 IS 알고리즘을 시행하면 어떻게 될까요?

얼추 정렬이 되는 것 같습니다. 그러나 이 과정을 한 번 거친다고 작은 접미사가 완전히 정렬되는 것은 아닙니다. (위 애니메이션에서는 6 2 0 4 8 순서로 있을 때, 최종 상태가 2 6 0 8 4가 됩니다. 접미사 2는 접미사 6보다 큽니다.)

조금 더 깊이 생각해 보겠습니다. 먼저 접미사 $i$의 접미사 크기 문자열 $\phi_{i}$을 다음과 같이 귀납적으로 정의합니다.

• $\phi_{n-1}$은 L입니다.
• $0 \leq i \leq n - 2$에 대해
  • 접미사 $i$가 작은 접미사인 경우 $\phi_{i}$는 S와 $\phi_{i+1}$을 이어붙인 문자열입니다.
  • 접미사 $i$가 큰 접미사인 경우 $\phi_{i}$는 L과 $\phi_{i+1}$을 이어붙인 문자열입니다.

쉽게 얘기하면 그림에서 각 접미사 위치의 색을 S와 L로 문자열로 나타낸 것입니다. 위 애니메이션에서 접미사 $2$의 접미사 크기 문자열은 SLSLSLSLLL입니다.

작은 접미사의 첫 글자만이 올바른 위치로 정렬되어 있다면,

• 문자열을 작은 접미사를 기준으로 모두 끊어서 연속된 큰 접미사 구간만 보면 (c)는 여전히 맞습니다. 따라서 2번 과정을 완전히 시행하면 연속된 파란색 부분까지 정렬됩니다. 즉 접미사 크기 문자열에서 L⁺S만 보았을 때 올바르게 정렬되어 있습니다.
• 그런 뒤 작은 접미사를, 4번 과정에서 연속된 파란색 부분만 맞는 큰 접미사를 기준으로 정렬합니다. 따라서 작은 접미사는 연속된 빨간색 이후 연속된 파란색 부분이 등장할 때까지만 보면 정렬된 상태입니다. 즉 접미사 크기 문자열에서 S⁺L⁺S만 보았을 때 올바르게 정렬되어 있습니다.

그런데 맨 앞에 있는 L을 제외하면, 전체 문자열을 (S⁺L⁺)⁺와 같은 형태로 쓸 수 있습니다. 그리고 우리는 작아진 접미사의 순서만이 필요하기 때문에, 맨 앞에 있을 수 있는 L을 무시할 수 있습니다. 다시 말하면, 우리는 작아진 접미사를 다음 작아진 접미사가 나올 때까지 정렬했다는 뜻이 됩니다.

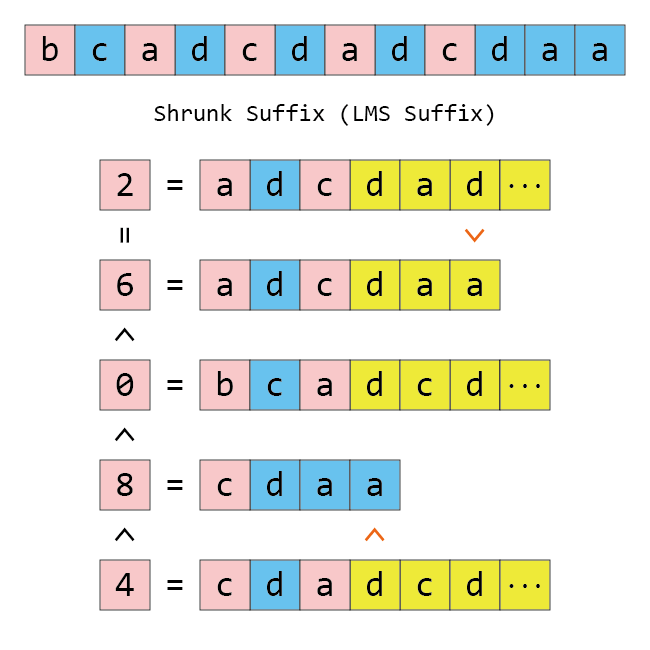
먼저 사소하지만 중요한 점을 짚고 넘어갑시다. Shrunk Suffix는 “작아진 접미사”의 영문 번역을 제가 마음대로 붙인 것입니다. 논문에서는 저희가 작아진 접미사라고 부르는 걸 LMS Suffix라고 부르는데, LMS는 LeftMost S-type의 준말입니다. S-type Suffix는 작은 접미사이니까 그렇다고 하더라도, 가장 왼쪽의 작은 접미사? “작아진 접미사”는 접미사 $0$을 절대로 포함하지 않고, LMS Suffix도 그렇습니다! LMS Suffix와 작아진 접미사의 정의는 같습니다. 따라서 가장 왼쪽이라는 말은 약간 부적절한 감이 있습니다.

다음으로, 작아진 접미사 위치가 두 번 등장했다면 그 다음부터는 노란색 칠을 해서 구분했습니다. 접미사 $2$와 접미사 $6$을 보면, 위에서도 적혀 있듯이, 접미사 $2$가 명백히 큰데 접미사 $6$보다 앞에 와 있습니다. 하지만 처음으로 달라지는 위치가 모두 노란색으로 칠해져 있으므로 작아진 접미사 사이만 볼 때는 아무래도 괜찮고 두 접미사는 같다고 볼 수 있습니다.

마지막으로 접미사 $8$과 접미사 $4$를 보면, 접미사 $9$와 접미사 $5$가 이미 올바르게 정렬되어 있었기 때문에 두 작아진 접미사 사이의 크기가 맞아 보이지 않습니다. 하지만 우리는 작아진 접미사 사이의 구간을 정확하게 정렬하고자 하는 게 아니고, 만일 노란색 부분을 포함해서 올바르게 정렬되었다면 그것도 그것대로 괜찮습니다. 왜냐하면, 어떤 문자열을 만들었는지가 아니라, 이 문자열의 Suffix Array가 작아진 접미사를 올바르게 정렬하느냐만 중요하기 때문입니다. 만일 두 작아진 접미사 사이가 다르다면, 두 작아진 접미사 사이의 실제 크기에 관계없이 먼저 정렬된 쪽이 작다고 가정해도 좋습니다. 그래서 그림의 왼쪽 부분은 cdaa가 cda보다 큼에도 불구하고 접미사 $8$이 접미사 $4$보다 작은 것으로 표시되어 있습니다.

이 그림의 노란색을 제외하고 필요한 부분, 특히 가장 왼쪽의 부등호를 알아내는 데에는 시간이 얼마나 걸릴까요? 작아진 접미사를 다음 작아진 접미사까지만 보았을 때 같은지를 비교하는 데 전체 $\mathcal{O}(n)$밖에 걸리지 않습니다. 노란색이 아닌 각 문자는 위 그림에서 최대 두 번 등장했고, 각 문자는 최대 두 번 (이전 문자열이 있으면 그 문자열과 한 번, 이후 문자열이 있으면 그 문자열과 한 번) 비교되므로 문자열의 문자를 참조하는 횟수가 $4n$ 이하가 되기 때문입니다. 따라서 큰 문제는 없습니다.

이렇게 같은지를 비교해서 새로운 문자를 지정하면, 이 문자들만으로 전체 문자열을 표현할 수 있습니다. 이 문자열의 특징은

• 최대 길이는 $\frac{n-1}{2}$를 넘지 않고, 평균 길이는 $\frac{n}{3}$ 정도입니다.
• 이 문자열의 Suffix Array는 작아진 접미사의 상대 순서를 알려줍니다.

그렇다면 이 문자열로 재귀 호출을 돌리면, 작아진 접미사의 상대 순서를 알 수 있고, 이 순서를 알 수 있으면 이 순서대로 접미사를 넣고 IS 알고리즘을 돌리면 Suffix Array가 완성됩니다! 이렇게 하면 SA-IS 알고리즘이 완성되었습니다…?

Base Case

언제까지고 재귀 호출을 돌릴 수는 없습니다. SA-IS의 Base Case는 속도를 위해서 조금 특이한 조건을 택했습니다. SA-IS의 Base Case는 문자의 종류 $k$가 $n$과 일치하는 경우입니다. Skew algorithm에서 논의한 대로 문자 집합을 반드시 $\Sigma = \{0, 1, \cdots, k-1\}$을 쓰도록 강제하면 $\mathcal{O}(n)$만에 이 Base Case를 처리할 수 있는데, 첫 글자를 기준으로 나누면 첫 글자가 모두 다르기 때문에 재귀 호출을 진행할 필요없이 첫 IS 알고리즘 이후 종료해도 결과가 올바르기 때문입니다.

이 경우 문자열의 길이 $n = 0$으로 재귀 호출이 일어나는 것이 가능한데, 이렇게 해도 전체 결과가 올바를 수밖에 없습니다. $n = 0$으로 재귀 호출이 일어났다면 큰 접미사 다음 작은 접미사가 오는 일이 없다는 뜻이고, 그렇다면 $\phi_{0}$이 S^*L⁺이 되어야 합니다. 이러면 IS 알고리즘을 두 번 돌렸을 때 S^*L^*S^*L^*S가 정렬되므로, 전체 길이의 접미사가 모두 고려된 채 정렬됩니다.

전체 알고리즘 정리

전체 알고리즘을 정리하면 다음과 같습니다.

1. 만일 사용된 문자의 수 $k = n$이라면,
   • 첫 글자를 기준으로 각 접미사를 첫 글자의 순서에 해당하는 위치에 집어넣습니다.
   • 이것이 곧바로 Suffix Array가 됩니다. 이 배열을 반환합니다.
2. 각 접미사의 크기를 구합니다.
   • 접미사 $(n-1)$는 큽니다.
   • $i = n-2$부터 $i = 0$까지 $1$씩 줄여 가면서,
   • $i$번째 문자가 $(i+1)$번째 문자보다 크다면, 접미사 $i$는 큽니다.
   • $i$번째 문자가 $(i+1)$번째 문자보다 작다면, 접미사 $i$는 작습니다.
   • $i$번째 문자가 $(i+1)$번째 문자와 같다면, 접미사 $i$의 크기는 접미사 $(i+1)$의 크기와 같습니다.
3. 작은 접미사를 Suffix Array의 첫 번째 문자가 일치하는 위치에 집어넣고, IS 알고리즘을 시행합니다.
4. 각 작아진 접미사에 대해,
   • 다음 작아진 접미사 직전까지 일반적인 문자열 비교를 시행합니다.
   • 이렇게 비교했을 때, 각 작아진 접미사가 몇 번째로 큰지 저장해 둡니다.
5. 각 작아진 접미사를 새로 정의된 순서로 바꾸어 쓴 뒤, 이 문자열로 SA-IS 알고리즘을 재귀 호출합니다.
6. 작아진 접미사를 Suffix Array의 첫 번째 문자가 일치하는 위치에 순서대로 집어넣고, IS 알고리즘을 시행합니다.
7. 이제 Suffix Array는 올바릅니다. 이 배열을 반환합니다.

시간 측정

위에서 소개한 두 개의 알고리즘은 Skew 알고리즘과 SA-IS 알고리즘입니다. 이 두 알고리즘은 여기에 구현되어 있습니다. 구현은 메모리가 굉장히 최적화되어 있으며, 전처리 $\mathcal{O}(\min(n \log n), n + \Sigma)$ 이후 Skew의 경우 $4n + \mathcal{O}(1)$ 워드, SA-IS의 경우 $3n + \mathcal{O}(1)$ 워드와 $2n + \mathcal{O}(1)$ 비트만을 추가로 사용합니다.

구현된 프로젝트에서 ./test를 이용해서 시간 측정을 해 볼 수 있습니다. 아래 표는 그 결과입니다. 염기 서열 분석에 사용되는 상황을 가정하고 모든 테스트에서 $|\Sigma| = 4$를 사용했습니다.

$n$	Skew ($2/3$-SA, sec)	SA-IS ($1/2$-SA, sec)
$40960$	0.00	0.00
$81920$	0.01	0.01
$163840$	0.02	0.01
$327680$	0.05	0.03
$655360$	0.11	0.06
$1310720$	0.24	0.13
$2621440$	0.56	0.29
$5242880$	1.54	0.74
$10485760$	5.09	1.98
$20971520$	14.97	4.51
$41943040$	36.17	9.89
$83886080$	81.17	21.50

Skew 알고리즘은 locality가 거의 보장되지 않는 Counting Sort가 굉장히 빈번하게 활용되어, $n$이 커질수록 SA-IS에 비해 기대하는 $1.5$배 차이보다 훨씬 긴 시간이 걸리는 것을 알 수 있습니다.

결론

어쨌거나 저는 작업하는 프로젝트에 SA-IS를 C++로 구현하고, Python의 ctypes를 활용해서 나머지 구현의 편의까지 모두 챙겨갔습니다. 처음에는 Skew를 구현했는데, 기다려 줄 만했지만 그래도 오래 걸린다는 생각에 SA-IS를 재구현했고 이제 더 이상 이 프로젝트의 병목은 문자열 검색이 아닙니다. 이처럼 Suffix Array를 선형 시간에 구성하는 것은 실질적인 도움도 있다 할 수 있겠습니다.

또 SA-IS는 Skew 알고리즘에 비해 이론적으로도, 실질적으로도 훨씬 빠르다는 것을 알 수 있었습니다.

References

[1] Kärkkäinen, J., & Sanders, P. (2003, June). Simple linear work suffix array construction. In International colloquium on automata, languages, and programming (pp. 943-955). Springer, Berlin, Heidelberg.

[2] D. K. Kim, J. S. Sim, H. Park, and K. Park. Linear-time construction of suffix arrays. In Proc. 14th Annual Symposium on Combinatorial Pattern Matching. Springer, June 2003.

[3] Ko, P., & Aluru, S. (2003, June). Space efficient linear time construction of suffix arrays. In Annual Symposium on Combinatorial Pattern Matching (pp. 200-210). Springer, Berlin, Heidelberg.

[4] Nong, G., Zhang, S., & Chan, W. H. (2009, March). Linear suffix array construction by almost pure induced-sorting. In 2009 Data Compression Conference (pp. 193-202). IEEE.