알고리즘 문제 접근 과정 6

이번 포스트에서도 ‘알고리즘 문제 접근 방법’ 시리즈에서 진행했듯이 특정 문제를 해결하기 위해 가장 낮은 단계의 접근에서부터 최종 해법까지 해결해나가는 과정을 작성합니다.

최대한 다양한 유형의 문제들을 다루어, 많은 문제 유형에서의 접근 방법에 대한 실마리를 드리는 역할을 하려 합니다.

Exhibition - JOI 2019 2번

주어진 문제가 영문이기 때문에 번역을 하여 문제를 첨부하겠습니다.

문제

알고박물관에서는 새해를 맞이해 여러 작품들을 특별 전시하려 합니다. 이번 특별 전시는 매우 귀한 작품들을 가지고 전시할 것이기 때문에, 전시하는 모든 작품들을 액자에 끼워서 전시하려 합니다. 알고박물관에서는 특별 전시를 위한 작품 N개의 후보를 뽑았습니다. 1번부터 N번까지의 각 작품들은 크기 Si와 작품의 가치 Vi를 가지고 있습니다. 알고박물관은 특별전시를 위한 M개의 액자를 가지고 있습니다. 각 액자는 크기 Cj를 가지고 있고, 이 액자에는 크기가 Cj이하인 작품들만 넣을 수 있습니다. 또한 한 액자에는 최대 하나의 작품만 넣을 수 있습니다.

특별전시는 관람객의 편의를 위해 다음과 같은 순서로 전시하려 합니다.

액자들은 크기가 항상 작거나 같아지는 순서로 놓기(액자 번호순일 필요는 없음)
액자 내 작품의 가치들이 항상 작거나 같아지는 순서로 놓기

알고박물관은 위 두 조건을 만족하면서 최대한 많은 작품을 전시하고 싶습니다. 알고박물관이 전시할 수 있는 작품의 수는 몇 작입니까?

예시

각 작품이 (크기, 가치)를 가지고 있다고 할 때, 3개의 작품이 각각 (10, 20), (5, 1), (3, 5)를 가지고 있고, 4개의 액자가 각각 4, 6, 10, 4의 크기를 가지고 있으면, 3번째 액자에 1번 그림을, 2번 액자에 2번 그림을 넣으면 총 2개의 작품을 전시할 수 있습니다.

입력

첫 번째 줄에 공백을 사이에 두고 작품의 수 N(1 <= N <= 10^5), 액자의 수 M(1 <= M <= 10^5)가 주어집니다. 두 번째 줄부터 N개의 줄에 거쳐 각각의 작품의 크기 $S_{i}(1 <= S_{i} <= 10^9)$, 작품의 가치 $V_{i}(1 <= V_{i} <= 10^9)$가 주어집니다. 이후 M개의 줄에 거쳐 각 액자의 크기 $C_{j}(1 <= C_{j} <= 10^9)$이 주어집니다.

출력

첫 번재 줄에 알고박물관이 전시할 수 있는 최대 작품의 수를 출력합니다.

풀이

만약 전시를 한다면 어떤 액자들을 사용하는 것이 좋을까요?

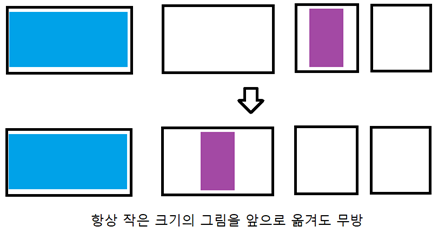
5개의 액자가 크기가 큰 순서대로 놓여있을 때, 실제론 3개의 그림을 각각 첫번째, 네번째, 다섯 번째 액자에 넣는다고 해봅시다. 그렇다면 이 때, 네번째 그림과 다섯 번째 그림을 각각 두번째, 세번째 액자에 넣을 수는 없을까요? 현재 액자는 크기 순서대로 정렬되어있기 때문에 위처럼 옮기는 일은 항상 가능합니다. 즉, 답이 어떻게 되든 간에 우리는 항상 액자를 가장 큰 액자부터 써도 무방하다는 것을 알 수 있습니다.

또한, 항상 액자에 들어가는 그림은 가치가 큰 것에서 작은 것으로 작아져야하기 때문에, 그림도 가치가 내림차순이 되도록 정렬을 해줄 수 있습니다.

여기에서, 우리는 다음에 해당하는 값을 구해볼 수 있을까요?

$F[i, j]$ = (i번 그림까지 봤을 때, j번 액자까지 넣을 수 있는 그림의 최대 개수)

만약 위 식을 모든 i, j에 대해 답을 알게된다면, N번 그림까지 봤을 때 M번 액자까지 넣을 수 있는 그림의 최대 개수가 곧 우리가 구하고자 하는 답이므로, $F[N, M]$이 답임을 알 수 있습니다.

그러면 어떻게 $F[i, j]$를 구할 수 있을까요? 만약 1 ~ i, 1 ~ j까지의 $F[i, j]$가 다 구해져있고, $F[i, j]$만 구하지 못한 상태라면 어떻게 할 수 있을까요? 특히 이 때, i번 그림을 j번 액자에 넣을 수 없다면, F[i, j]는 어떻게 될까요?

이 때는 항상 두 가지 경우가 있을 수 있을 것입니다. 1번부터 i-1번 그림들을 j번 액자까지 넣었을 수도 있고, 혹은 1번부터 i번 그림들을 j-1번 액자까지에 넣었을 수도 있습니다(다른 모든 경우는 이 두 경우 중 하나에 포함됩니다).

위 두 경우를 통해 우리는

F[i, j] = MAX(F[i – 1, j], F[i, j – 1]) 이 된다는 것을 알 수 있습니다.

그렇다면, 만약 i번 그림을 j번 액자에 넣을 수 있다면 어떻게 될까요? 이 때에는 1 ~ i-1번을 1 ~ j-1번 액자에 넣고, i번 그림을 j번 액자에 넣을 수도 있기 때문에 앞선 경우에 하나를 더 추가해줘야 합니다. 즉, 이를 통해 $F[i, j]$는

$F[i, j] = MAX(F[i – 1, j – 1] + 1, F[i – 1, j], F[i, j – 1])$

이 됩니다.

우리는 결국 모든 i, j에 대해서 $F[i, j]$를 구해줄 수 있고, 답은 F[N, M]이 될 것입니다. 이 때, $F[N, M]$을 구하는데 걸리는 시간은 모든 i, j를 계산하는 시간과 같으므로, 총 O(NM)이 됩니다.

풀이 - 최적화

위 방법을 문제의 특수한 성질을 통해 더 빠르게 계산할 수 있을까요?

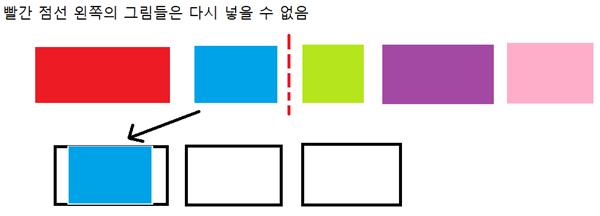
만약 정렬을 한 이후, 첫 액자에 하나의 그림을 넣어야 한다면, 어떤 그림을 넣는 것이 좋을까요? 당연히 그 액자에 넣을 수 있는 최대 가치를 가진 그림을 넣어야 할 것입니다. 이 때, 1번 액자에 넣은 그림을 i번이라고 한다면, 2번 액자에 1 ~ i-1번에 있는 그림을 넣을 수 있을까요? 이는 특별전시의 두 번째 조건인 항상 가치가 낮은 순서가 되어야한다는 것을 만족하지 못하므로, i번 그림을 첫 액자에 넣고 나면, 2번 액자에 넣을 수 있는 그림은 항상 i+1번 이후의 그림이 됩니다.

그림을 항상 증가하는 방향으로만 보게 됨

즉, 우리는 앞에서부터 그림을 살펴보면서 액자에 넣게 된다면, 그 이후에도 항상 다음 그림들만 보면 된다는 것을 알 수 있습니다.

여기서 액자에 넣는 조건은 항상 넣을 수 있는 크기이기만 하면 되므로(가치순서로 정렬되어있으므로) 앞에서부터 순서대로 그림을 보면서 액자에 넣어주는 것으로 문제를 해결할 수 있어, 전체 시간복잡도는 정렬은 하는데 걸리는 시간인 $O(NlgN + MlgM)$이 됩니다.

이 때 추가로, 같은 가치를 가지는 그림들은 항상 크기가 큰 순서가 앞에 오도록 정렬하면, 액자에 넣는 순서가 변하지 않게 되어 항상 답을 구할 수 있습니다.

[화장실]

해당 문제는 번역본이 아닌, 비슷한 유형으로 증명되고 적용되는 많은 경우들을 대표해서 알려드리기 위해 제작한 문제입니다. 여러분이 문제를 푸시다가 이와 같거나 비슷한 유형의 아이디어와 증명 방법을 사용할 일이 많을 것입니다.

문제와 입출력 형식을 같이 첨부하겠습니다.

문제

알고공원 화장실에는 한 개의 변기만 존재한다. 이에 공원 화장실을 이용하는 사람들은 한 줄로 서서 화장실을 이용하며, 자기의 앞에 서있는 사람들이 모두 이용하고 나야지만 화장실을 이용할 수 있다.

사람들은 각자 화장실을 이용하는 시간이 모두 다르므로, 어떤 사람은 적은 시간만에 이용을 할 수도 있고, 어떤 사람은 오랜시간동안 화장실을 사용할 수도 있다.

어느날, 알고공원 화장실에는 N명의 사람들이 동시에 화장실을 이용하려고 도착하여 줄이 엉망이 되었다. 이에 공원관리자 민솔이는 어떻게 줄을 서게 하면 좋을까 생각하다가, ‘모든 사람들이 화장실을 이용하는데 걸리는 시간의 합’을 최소화하게 줄을 세우기로 하였다.

예를 들어 총 4명이 있고, 각 사람들이 화장실을 이용하는데 1, 4, 3, 8 만큼의 시간이 걸린다 하면, 이를 순서대로 이용하게 하면 1번 사람은 0분만에, 2번 사람은 1분만에, 3번 사람은 1 + 4 = 5분만에, 4번 사람은 1 + 4 + 3 = 8분만에 화장실을 이용할 수 있으므로, 모든 사람들이 화장실을 사용하기 위해 기다린 시간의 합은 0 + 1 + 5 + 8 = 14가 된다.

하지만 만약 줄을 1번, 3번, 2번, 4번 순으로 세우면, 1번 사람은 0분, 3번 사람은 1 = 1분, 2번 사람은 1 + 3 = 4분, 4번 사람은 1 + 3 + 4 = 7분이 되므로 총 합은 0 + 1 + 4 + 7 = 12분이 되고, 이 때가 모든 가능한 경우들 중 최소가 된다.

화장실을 이용하는 사람의 수 N과 각 사람들이 화장실을 이용하는데 걸리는 시간이 주어졌을 때, 민솔이가 최적으로 줄을 세웠을 때의 ‘모든 사람들이 화장실을 사용하기 위해 기다린 시간’의 최솟값을 구하여라.

예시

원문에서 나온 예시가 주어진 4명의 사람들이 화장실을 사용하는데 걸린 시간의 합을 최소로 만드는 방법이다.

입력

첫째 줄에 사람의 수 N(1 <= N <= 10^5)이 주어진다. 둘째 줄에 각 사람이 화장실을 이용하는데 걸리는 시간 $T_{i}(1 <= T_{i} <= 10^3)$가 공백을 사이에 두고 주어진다.

출력

각 사람이 화장실을 사용하기까지 걸리는 시간의 합의 최솟값을 출력한다.

입력 예제

1 4 3 8

출력 에제

관찰

어떤 한 사람이 화장실을 이용하는데 걸린 시간은 자신의 앞에 줄 서 있던 사람들이 이용하기까지 걸린 시간과 자기 자신이 화장실을 사용하는데 걸린 시간의 합이 됩니다.

사람들이 화장실을 가는 최소의 시간을 구하는 가장 쉬운 방법은 무엇일까요? 만약 우리가 사람들이 줄을 서게되는 모든 경우를 다 따지게 된다면 총 N! 만큼의 경우의 수들이 있고, 각 사람들이 화장실을 이용하는데 얼마의 시간이 걸리는지 확인하기 위해 N명의 사람들을 순서대로 보면서 사용하는데 걸린 시간을 다 구해주어야하기 때문에 총 $O(N * N!)$ 만큼의 시간이 걸리게 됩니다.

하지만 이러한 방법은 사람들이 10명만 넘어가도 시간이 굉장히 오래 걸리게 됩니다. 우리는 각 사람들이 화장실을 이용하는데 걸리는 시간을 이용하여, ‘모든 경우를 따지지 않고, 최적의 방법을 찾아내야합니다.’

그렇다면 어떤 식으로 줄을 세워야할까요? 이를 위해선 우린 주어진 정보를 살펴볼 필요가 있습니다.

각 사람들마다 화장실을 이용하는 시간은 천차만별이 될 수 있습니다. 어떤 사람은 이용하는 1분이면 모두 이용하는데 반해, 어떤 사람은 1시간이 걸리는 경우도 있을 것입니다. 이처럼 각 사람들이 ‘화장실을 이용하는데 걸리는 시간이 정보’ 가 될 수 있습니다. 또한, 우리는 이 사람들이 ‘화장실을 이용하는데 걸리는 시간 외에는 아무런 정보도 없다’ 는 사실도 정보가 될 수 있습니다. 즉, 우리는 주어진 이 시간들을 이용해 최적의 방법을 찾아내야만 합니다.

주어진 문제에서 사람들이 굉장히 많이 나오기 때문에 이 모든 경우를 생각해보는 것은 쉽지 않은 일입니다. 그렇기 때문에 우리는 굉장히 단편적인 상황을 예시로 들어 생각해보는 것도 좋은 접근방법입니다.

풀이

만약 2명의 사람이 화장실을 이용하기 위해 대기하고 있고, 1번 사람은 1만큼의 시간이, 2번 사람은 2만큼의 시간이 걸린다고 합시다. 이 때, 줄을 세울 수 있는 방법은 2가지만 존재하게 되는데, 이 중 어떤 경우가 최적이 되는지 살펴봅시다.

만약 1, 2번 순으로 줄을 세운다면 1번 사람은 0, 2번 사람은 1만큼의 시간이 걸려 총 1의 시간이 걸리게 됩니다.
하지만 2, 1번 순으로 줄을 세운다면 2번 사람은 0, 1번 사람은 2만큼의 시간이 걸리므로 총 2의 시간이 걸려 위의 경우보다 더 좋지 않은 결과를 내게 됩니다.

이는 일반화된 2명의 사람일 때를 고려하더라도, 항상 더 시간이 적게 걸리는 사람이 먼저 화장실을 이용하는 것이 좋은 결과를 내게 됩니다. 그렇다면 우리는 다음과 같은 방법을 생각해 볼 수 있습니다.

항상 이용하는 시간이 작은 순서대로 화장실을 사용하는 것이 최소가 되지 않을까?

만약 앞서 사용한 사람이 일짝 나온다면, 그 다음 사람도 일찍 이용할 수 있게 되고, 그 다음 사람도 더 일찍 이용할 수 있으므로 어느정도 합리적인 것 같은 방법입니다. 그렇다면 이 방법이 실제 답이되는지는 어떻게 증명할 수 있을까요?

모든 사람들을 이용하는 시간이 작은 순서대로 배치한다는 것은, 어느 사람이라도 자기의 앞 사람이 항상 자신보다 이용시간이 작거나 같다는 것과 같은 말이 됩니다. 우리는 이 바뀐 조건을 이용해 증명해봅시다.

만약 화장실을 a 시간동안 이용하는 사람 바로 앞에, 이보다 이용시간이 긴 b인 사람이 있다고 생각해봅시다(a < b).

이 때, 각 사람들을

b 앞에 있는 사람들
a, b
a 뒤에 있는 사람들

로 나누어 생각해보면,

a, b 앞에 있는 사람들은 a와 b가 어떤 순서로 있든 영향을 받지 않으므로 고려할 필요가 없게 됩니다
a 앞에 b가 있으면, b가 a 앞에 있을 때보다, b - a만큼 더 오랜시간이 걸리게 됩니다
a, b 뒤에 있는 사람들은 a와 b가 어떤 순서로 있든 영향을 받지 않으므로 고려할 필요가 없게 됩니다.

결국, 서로 연달아 있는 a, b 두 사람은 어떤 순서로 있든지 나머지 사람들에게 영향을 주지 않으므로, 항상 a, b 두 사람이 이용하는 시간이 작은 때가 더 좋은 결과를 내게 됩니다. 이 때에, 항상 이용시간이 더 긴 b가 뒤에 있으면 좋다는 것을 알 수 있습니다.

이를 모든 앞뒤로 있는 사람들에게 적용한다면, 언제나 뒤에 있는 사람이 앞 사람보다 이용시간이 길거나 같아야하고, 이는 앞서 말한 ‘이용시간이 작은 사람부터 이용한다’ 는 것이 됩니다.

즉, 우리는 이 문제를 모든 사람들이 이용하는데 걸리는 시간을 정렬하는 것으로 순서를 바로 확정할 수 있고, 정렬에 걸리는 $O(NlgN)$ 시간복잡도에 해결할 수 있습니다.

코드

Exhibition

#include <bits/stdc++.h>
using namespace std;

struct Data{ int s, v; };

int n, m, res;
int carr[100010];
Data arr[100010];

bool compare(Data d1, Data d2){
	if(d1.v == d2.v) return d1.s < d2.s;
	return d1.v < d2.v;
}
int main(){
	int i, j;
	scanf("%d %d", &n, &m);
	for(i = 0; i < n; i++) scanf("%d %d", &arr[i].s, &arr[i].v);
	for(i = 0; i < m; i++) scanf("%d", &carr[i]);
	sort(arr, arr + n, compare);
	sort(carr, carr + m);
	j = n - 1;
	for(i = m - 1; i >= 0; i--){
		for(; j >= 0; j--){
			if(carr[i] >= arr[j].s){
				res++;
				break;
			}
		}
		j--;
	}
	printf("%d", res);
	return 0;
}

화장실

#include <bits/stdc++.h>
#define ll long long
using namespace std;

int n;
ll res;
int arr[100010];

int main(){
	int i, sum = 0;
	scanf("%d", &n);
	for(i = 0; i < n; i++) scanf("%d", &arr[i]);
	sort(arr, arr + n);
	for(i = 0; i < n; i++){
		res += sum;
		sum += arr[i];
	}
	printf("%lld", res);
	return 0;
}

알고리즘 문제 접근 과정 6

알고리즘 문제 접근 과정 6

Exhibition - JOI 2019 2번

문제

예시

입력

출력

풀이

풀이 - 최적화

[화장실]

문제

예시

입력

출력

입력 예제

출력 에제

관찰

풀이

코드

Exhibition

화장실

Faster and Simpler Algorithm for Sorting Signed Permutations by Reversals

Bostan-Mori Algorithm