MRI imaging과 Parallel Imaging Algorithm, 그리고 PRUNO

Introduction

MRI (Magnetic Resonance Imaging)은 X-Ray, CT와 함께 널리 쓰이는 의료 영상 기법으로 손꼽힙니다. 이미지 특성 상 가장 좋은 연부 조직 대비 (soft matter contrast)를 보여줍니다. 즉, 근육이나 뇌 등 수분을 많이 포함하는 조직에 대해 가장 월등한 이미지 품질을 낼 수 있습니다. 다만 MRI의 경우 짧게는 30분에서 1시간 정도 되는 긴 촬영 시간이 단점으로 꼽히는데, 때문에 시간 단축을 위한 다양한 기법이 제시되고 있습니다.

MRI는 촬영한 raw data가 전자기파 신호이기 때문에, 특이하게도 이를 푸리에 변환을 비롯한 몇 가지 가공을 통해 이미지를 완성해야 합니다. 번거로운 과정일 수 있지만, 반대로 생각해 보면 시간 단축을 위해 “k-space”의 데이터를 사용할 수 있다는 이점이 생긴 것이기도 합니다. 이 글에서는 MRI 이미지 생성하는 데 드는 시간을 줄이는 기법 중 하나인 PI (Parallel Imaging)에 대해 간단히 알아보고, 이 방법 중 하나인 PRUNO (Zhang et al, 2011)에 대해 간단히 리뷰합니다.

Acquiring the MR image

이 문단의 내용은 Deshmane 2012 에 의존하고 있습니다.

Key features for MR image quality

가장 일반적으로 쓰이는 2DFT Cartesian 기법의 경우, MRI 이미지에서는 $k$-space data $f(k _ {x}, k _ {y})$를 얻게 됩니다. 이 때 원래 이미지 $F(x, y)$와 $f(k _ {x}, k _ {y})$의 관계는 Fourier transform으로 연결되어, $F(x, y) = \mathcal{F}{f}(x, y) = \int e^{ik _ {x} x} e^{ik _ {y}y} f(k _ {x}, k _ {y}) dk _ {x} dk _ {y}$와 같이 표현됩니다. 하지만 모든 데이터는 이산적이고 유한하기에, 위 식과 같이 연속적인 결과를 얻을 수는 없습니다. 따라서 실제로는

Band Limit : $k _ {x}, k _ {y}$의 절댓값에 upper bound $K _ {x}, K _ {y}$가 생깁니다. $K _ {x}, K _ {y}$가 클수록 이미지의 해상도 (resolution)이 좋아집니다.
Sampling Rate : $dk _ {x}, dk _ {y}$는 충분히 작은 간격인 $\Delta k _ {x}$, $\Delta k _ {y}$로 대체됩니다. Sampling이 촘촘할수록 담을 수 있는 이미지의 크기 (FOV, Field-Of-View) 가 커지게 됩니다.

이 때 FOV가 이미지의 크기보다 작은 경우, 아래 그림의 D와 같이 이미지가 여러 번 겹쳐 보이는 aliasing 현상이 나타나게 됩니다.

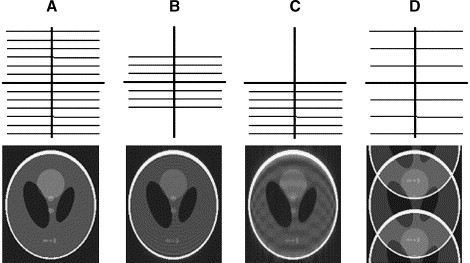
aliasing

따라서 좋은 이미지 퀄리티를 얻기 위해서는 $K _ {xy}, \Delta k _ {xy}$를 모두 신경써주어야 합니다.

Cost for MR Imaging

그렇다면, 이미지를 얻기 위해 필요한 시간을 결정하는 인자는 무엇일까요? 가장 일반적인 촬영 기법에서는 $k _ {y}$ (“phase encoding”)를 고정해놓고, $k _ {x}$축과 평행한 직선 (phase encoding line)을 따라 data point를 빠르게 읽어내는 (“readout”) 방법을 사용합니다. 때문에 촬영에 드는 시간은 phase encoding line의 개수, 즉 $K _ {y} / \Delta k _ {y}$에 가장 큰 영향을 받게 됩니다. 따라서, 오늘은 촬영 가속화 기법 중에서 phase encoding line의 개수를 줄이는 기법들을 알아볼 것입니다.

몇 가지 고전적인 기법으로는 다음과 같은 것들이 있습니다.

Phase Resolution: 위 그림의 B와 같이, $\Delta k _ {y}$를 그대로 두고 $K _ {y}$를 줄인 뒤, $k _ {y}$가 큰 영역에는 zero-padding을 하는 방법입니다. 이미지에 다소 noise가 낀 모습을 볼 수 있습니다.
Partial Fourier: 위 그림의 C와 같은 방법입니다. 이미지가 실수값을 가진다고 가정하면, k-space 데이터는 Hermitian이 됩니다. 즉 $f(-k _ {x}, -k _ {y}) = f^{*}(k _ {x}, k _ {y})$가 되므로 이를 이용해서 $k _ {y} < C$인 반쪽 (대개 5/8~7/8)영역에 대해서만 데이터를 얻고 나머지를 복원합니다.
Parallel imaging : 위 그림의 D와 같은 방법으로, $\Delta k _ {y}$를 늘린 “aliased image”를 만들고, 이러한 이미지를 여러 장 겹쳐서 복원합니다.

Reconstruction of Parallel Image

이 단원의 이미지 출처는 모두 https://mri-q.com/how-is-pi-different.html 임을 밝힙니다.

SENSE : resolving aliasing

pi1

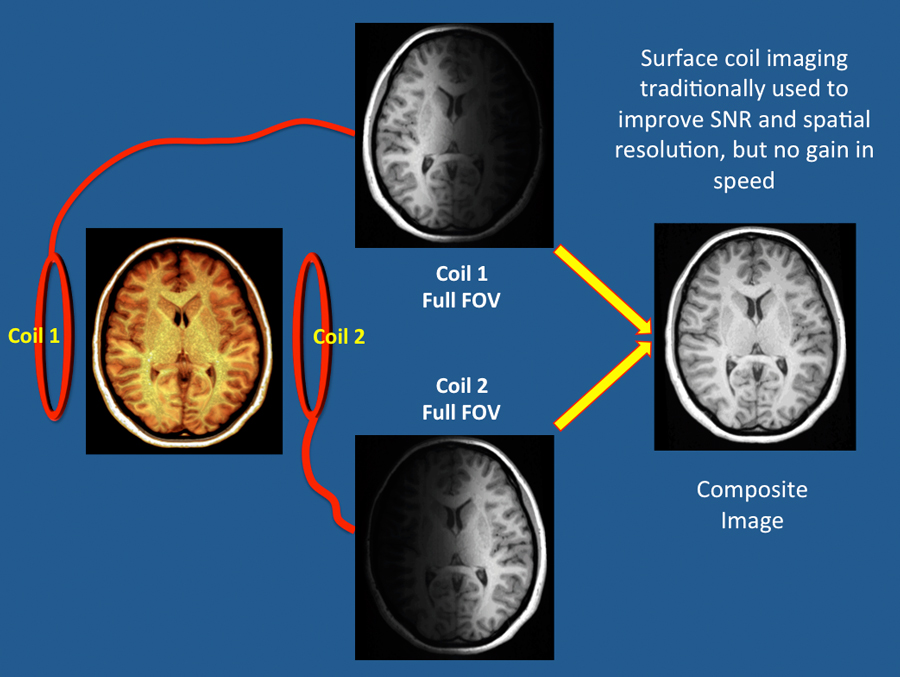
실제로 우리가 보게 되는 MR image는 사진 한 장이 아니라, 여러 개의 수신기 (코일)을 통해 얻은 이미지를 합친 것에 가깝습니다. 코일의 위치에 따라서 신호가 더 잘 잡히는 (sensitive) 영역이 다르기 때문에, 원본 이미지를 복원하기 위해서는 coil combining 과정을 거치게 됩니다. 그런데 이 과정을 aliasing 제거를 위해 사용할 수 있습니다!

pi2

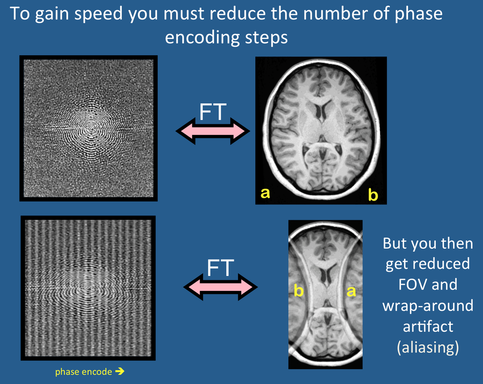
보시는 바와 같이, $\Delta k _ {y}$를 절반으로 줄이면 (undersampling) 얻게 되는 phase encoding line의 개수가 절반으로 줄어들어 촬영 시간이 감소하게 됩니다. 하지만 이 경우 아래 이미지처럼 aliasing이 발생하는 것을 알 수 있습니다.

Aliasing이라는 것은 결국 한 점 $(x, y)$의 밝기 (intensity) $I(x, y)$에 다른 여러 점이 겹쳐 보이는 것에 지나지 않습니다. 즉, $I _ {\textrm{aliased}}(x, y) = \sum _ {k = -\infty}^{\infty} \sum _ {l = -\infty}^{\infty} I(x + k \cdot\textrm{FOV} _ {x}, y + l\cdot\textrm{FOV} _ {y})$라는 식으로 나타낼 수 있습니다.

위 그림에서 undersample하기 전 FOV는 이미지 크기보다 크므로, undersample 후에도 이미지가 두 번만 겹쳐졌다고 가정할 수 있습니다. 즉, 한 코일이 측정한 이미지의 밝기는 $I _ {\textrm{aliased}}(x, y) = I(x, y) + I(x, y - \textrm{FOV} _ {y})$로 나타낼 수 있습니다.

코일마다 sensitivity가 다르므로, 코일 $k$가 측정한 이미지 $I^{k}(x, y)$는 코일의 sensitivity function $S^{k}(x, y)$에 이미지의 “진짜 밝기” (보통은 magnetization) $m(x, y)$를 곱한 값으로 취급할 수 있습니다.

즉, $I _ {\textrm{aliased}}^{k}(x, y) = S^{k}(x, y)m(x, y) + S^{k}(x, y-\textrm{FOV} _ {y})m(x, y - \textrm{FOV} _ {y})$가 됩니다. 만약 서로 다른 코일 2개로 데이터를 측정했다면 다음과 같은 연립 방정식을 얻을 수 있게 됩니다.

$ \begin{bmatrix}I _ {\text{aliased}}^{1}(x, y) \ I _ {\text{aliased}}^{2}(x, y) \end{bmatrix} = \begin{bmatrix} S^{1}(x, y) && S^{1}(x, y - \text{FOV} _ {y})\S^{2}(x, y) && S^{2}(x, y - \text{FOV} _ {y}) \end{bmatrix} \begin{bmatrix} m(x, y) \ m(x, y- \mathrm{FOV} _ {y}) \end{bmatrix} $

즉, 두 sensitivity profile이 충분히 독립적이기만 하다면 $Ax = b$ 꼴의 방정식을 풀어 원래 이미지 $m(x, y)$를 모두 복원할 수 있습니다. 이런 방법론에 기초한 이미지 복원법을 SENSE (Pruessman 1999)라고 부릅니다. 이상적으로는 $R$배 undersample했을 때, “아주 좋은 $R$개 이상의 코일” (위 식이 solvable한 경우)만 있다면 aliasing을 제거할 수 있는 셈입니다. 이 때 이 코일들이 ideal configuration을 이룬다고 합시다.

Interpolating k-space

SENSE 알고리즘이 갖고 있는 단점은 Sensitivity map을 물리적으로 측정해야 한다는 점입니다. 이는 보통 환자 사진을 찍기 전에 prescan이라는 과정을 거쳐 측정하곤 하는데, 여하튼 이미지 외에 추가적인 정보를 필요로 한다는 점이 마음에 들지 않습니다. Griswold 2002에서 제시한 알고리즘인 GRAPPA를 필두로 한 알고리즘들이 이를 보완하는 방법 중 하나입니다.

코일에 의해 측정된 이미지 $I(x, y)$는 sensitivity map $S(x, y)$와 실제 magnetization $m(x, y)$의 곱으로 나타나므로, 이를 푸리에 변환하면 $k$-space는 두 함수의 convolution 형태로 나타날 것입니다. 즉,

$\tilde{I}(k _ {x}, k _ {y}) = \sum _ {k _ {x}^{\prime}, k _ {y}^{\prime}} \tilde{S}(k _ {x}^{\prime}, k _ {y}^{\prime}) \tilde{m}(k _ {x} - k _ {x}^{\prime}, k _ {y} - k _ {y}^{\prime})$과 같이 쓸 수 있습니다. 이 때, 다음과 같은 가정을 추가합니다.

“Sensitivity kernel” $\tilde{S}(k _ {x}, k _ {y})$는 크기 $w _ {S}$가 아주 작다.
- $S(x, y)$는 비오-사바르 법칙에 의존하는 함수로, 일반적으로 매우 smooth하다고 가정할 수 있습니다. 따라서 처음 몇 개의 푸리에 계수로 쉽게 근사할 수 있다고 가정합니다.
코일들은 ideal configuration을 이룬다.

이 조건을 가정하고, 우리가 원하는 관계식을 이끌어내봅시다. 그에 앞서 용어를 간단히 정의합니다.

첨자 문제로 길이 $n$짜리 벡터들의 공간을 $\mathbb{C}(n)$, $n \times m$ 행렬 (혹은 linear map)들의 공간을 $\mathbb{C}(n, m)$으로 씁니다.
k-space image는 전체 $N _ {x} \times N _ {y}$크기이다. $\mathbf{m} \in \mathbb{C}(N _ {x}N _ {y})$는 K-space domain에서의 magnetization $\tilde{m}$를 나타내는 값이다.
$\sigma^{i} \in \mathbb{C}(N _ {x}N _ {y}, N _ {x}N _ {y})$는 $i$번째 코일의 sensitivity kernel $\tilde{S}^{i}$를 나타낸다. 행렬로 쓸 수 있지만 본질적으로는 convolution이다.
코일의 개수를 $N _ {c}$로 쓰고, $\mathbf{S} = \begin{bmatrix} \sigma^{1} \ \vdots \ \sigma^{N _ c}\end{bmatrix} \in \mathbb{C}(N _ {c}N _ {x}N _ {y}, N _ {x}N _ {y})$로 정의한다.
$\mathbf{d} \in \mathbb{C}(N _ {c}N _ {x}N _ {y})$는 실제 코일 $1, \cdots, N _ {c}$에서 관찰된 K-space 데이터를 나타낸다. $\mathbf{d} = \mathbf{S}\mathbf{m}$을 만족한다.
이 때, undersample로 인해 $N _ {c}N _ {x}N _ {y}$의 데이터 중 $a$개의 데이터만 수집되고 (acquired) $m = N _ {x}N _ {y} - a$개의 데이터는 수집되지 않았다 (missed) acquired column만 $1$인 행렬을 $I _ {a}$, missed column만 1인 행렬을 $I _ {m}$으로 쓴다. Identity matrix $I = I _ {m} + I _ {a}$가 성립한다.

이 때, $\mathbf{d} = \mathbf{Sm}$에서 아직 모르는 데이터 $\mathbf{d} _ {m} = I _ {m}\mathbf{d}$를 아는 데이터 $\mathbf{d} _ {a} = I _ {a}\mathbf{d}$를 통해 구할 수 있는지가 관건입니다. $\mathbf{d} _ {m} = I _ {m}\mathbf{S}\mathbf{m} = \mathbf{S} _ {m}\mathbf{m}$, $\mathbf{d} _ {a} = I _ {a}\mathbf{S}\mathbf{m} = \mathbf{S} _ {a}\mathbf{m}$이므로 $\mathbf{d} _ {m} = \mathbf{S} _ {m} \cdot (\mathbf{S} _ {a}^{\dagger}\mathbf{S} _ {a})^{-1}\mathbf{d} _ {a} = \mathbf{R}\mathbf{d} _ {a}$와 같이 쓸 수 있고, 결국 $\mathbf{d} _ {m}$을 $\mathbf{d} _ {a}$만 가지고 표현할 수 있다는 뜻이 됩니다. 이에 따라 $\mathbf{N}\mathbf{d} = 0$을 만족하는 nontrivial “nulling kernel” matrix $\mathbf{N}$을 찾으면 $\mathbf{N}$의 null space에서 $\mathbf{d}$를 찾을 수 있고, 꽉 찬 k-space data로부터 full-FOV 이미지를 얻을 수 있게 됩니다. GRAPPA, 그리고 오늘 리뷰할 논문인 PRUNO는 모두 nulling kernel $\mathbf{N}$을 어떻게 얻는지에 초점을 맞추고 있습니다.

PRUNO : deriving nulling kernel

여기서부터 오늘의 주인공 PRUNO의 아이디어가 시작됩니다. Sensitivity kernel은 그 특성상 k-space를 평행이동해도 변하지 않으므로, nulling kernel 역시 k-space translation에 대해 변하지 않습니다. 또한, 이어질 논증을 통해 우리는 nulling kernel 자체도 작은 크기의 convolution kernel로 나타난다는 것을 보일 것입니다.

아이디어는 이웃한 $w _ {d} \times w _ {d}$ 크기의 블록을 모두 모았을 때, $w _ {d}$가 충분히 크기만 하다면 이들 사이에 linear dependence가 생긴다는 점입니다. K-space 위의 한 점 $(k _ {x}, k _ {y})$ 주변으로 $w _ {d} \times w _ {d}$ 개의 점을 모은 local data point $\tilde{\mathbf{d}} \in \mathbb{C}(N _ {c} w _ {d}^{2})$를 생각하면, sensitivity kernel이 convolution이기 때문에 local sensitivity kernel $\tilde{\mathbf{S}} \in \mathbb{C}(N _ {c}w _ {d}^{2}, (w _ {d} + w _ {s} - 1)^{2})$과 local magnetization $\tilde{\mathbf{m}} \in \mathbb{C}((w _ {d} + w _ {s} - 1)^{2})$에 대해 $\tilde{\mathbf{d}} = \tilde{\mathbf{S}}\tilde{\mathbf{m}}$으로 쓸 수 있게 됩니다. 이 때 $r = N _ {c}w _ {d}^{2} - (w _ {d} + w _ {s} - 1)^{2} > 0$이라면, $\mathbf{S}^{\dagger}$는 최소 $r$차원의 null space를 갖게 됩니다. $r$은 $(N _ {c} - 1)w _ {d}^{2}$ 스케일로 커지기 때문에 $w _ {d}$를 충분히 키우기만 하면 쉽게 $r > 0$을 달성할 수 있습니다.

이렇게 얻은 kernel을 $\tilde{\mathbf{n}} _ {1}, \cdots, \tilde{\mathbf{n}} _ {r} \in \mathbb{C}(N _ {c}w _ {d}^{2})$이라 두면 $\tilde{\mathbf{n}} _ {i}^{\dagger} \tilde{\mathbf{d}} = 0$을 만족하게 됩니다. 이 때 $\tilde{\mathbf{n}} _ {i}$는 channel이 $N _ {c}$개, 크기가 $w _ {d} \times w _ {d}$인 convolution kernel로 생각할 수 있습니다. 따라서 local nulling kernel matrix $\tilde{\mathbf{N}} = \begin{bmatrix} \tilde{\mathbf{n}} _ {1}, \tilde{\mathbf{n}} _ {2}, \cdots, \tilde{\mathbf{n}} _ {r}\end{bmatrix}^{\dagger} \in \mathbb{C}(r, N _ {c}w _ {d}^{2})$ 이 k-space data 사이의 선형 종속성을 나타내는 convolution kernel이 되고, 이 kernel을 각 k-space point에 적용하는 것으로 global nulling kernel $\mathbf{N} \in \mathbb{C}(rN _ {x}N _ {y}, N _ {c}N _ {x}N _ {y})$를 얻을 수 있습니다.

물론 아직 어떻게 $\tilde{\mathbf{n}} _ {1}, \cdots, \tilde{\mathbf{n}} _ {r} \in \mathbb{C}(N _ {c}w _ {d}^{2})$을 얻을 수 있는지는 논의하지 않았지만, 잠시 미루고 이후 문제를 어떻게 해결할지 생각해 볼 수 있습니다.

Iteratively solving the “null equation” - composed convolution kernels

Global nulling kernel $\mathbf{N}$이 $\mathbf{Nd} = 0$을 만족하기 때문에, $0 = I\mathbf{N}I\mathbf{d} = (I _ {m} + I _ {a})\mathbf{N}(\mathbf{d} _ {m} + \mathbf{d} _ {a}) = \mathbf{N} _ {m}\mathbf{d} _ {m} + \mathbf{N} _ {a}\mathbf{d} _ {a}$로 쓸 수 있고, 결국 $\mathbf{N} _ {m}\mathbf{d} _ {m} = -\mathbf{N} _ {a}\mathbf{d} _ {a}$를 풀어야 합니다. 또하나의 커다란 $Ax = b$ 문제를 풀어야 하는데, 적어도 $\mathbf{N} _ {m}$이 tall matrix여야 문제를 풀 수라도 있습니다. 즉 $rN _ {x}N _ {y} \ge mN _ {c}$가 성립해야 하고, 일반적으로 $R$번 건너 한 번 line을 얻는 $R$-factor undersampling 경우 $m \sim \frac{R-1}{R}N _ {x}N _ {y}$이니 $r \ge \frac{R-1}{R}N _ {c}$가 성립해야 합니다. 이에 비추어 사용해야 하는 $w _ {d}$의 값 또한 예상할 수 있습니다.

이후는 전형적인 선형 대수 문제로, 양변에 $\mathbf{N} _ {m}^{\dagger}$를 곱해 positive semidefinite form을 만들어 줍니다. 이제 풀어야 하는 방정식은

$ I _ {m} (\mathbf{N}^{\dagger}\mathbf{N}) I _ {m} \mathbf{d} = -I _ {m} (\mathbf{N}^{\dagger}\mathbf{N}) I _ {a} \mathbf{d}$와 같이 정리됩니다. 이는 conjugate gradient solver 등을 이용해서 풀어줄 수 있습니다. 문제는 $(\mathbf{N}^{\dagger}\mathbf{N})$이 너무 큰 행렬이라는 건데, 다행히 우리는 $\mathbf{N} \in \mathbb{C}(rN _ {x}N _ {y}, N _ {c}N _ {x}N _ {y})$이 pointwise convolution $\mathbf{N} _ {ij}$ ($i = 1, \cdots, r, j = 1, \cdots, N _ {c}$)의 block matrix 꼴로 나타난다는 사실을 알고 있습니다. CG solver는 행렬의 값을 다 알 필요가 없이 $x \mapsto Ax$만 평가할 수 있으면 돌아가기 때문에, 매 iteration마다 $O(rN _ {c})$번의 convolution을 수행해주면 문제를 해결할 수 있습니다.

다만 $r \gg N _ {c}$인 경우가 많으니 최적화를 한 번 더 해봅시다. $\mathbf{N}^{\dagger}\mathbf{N}$은 $\mathbf{D} _ {ij} = \sum _ {k = 1}^{r} \mathbf{N} _ {ik}^{\dagger} \mathbf{N} _ {kj}$의 block matrix로 나타나게 됩니다. 이 때 아래 사실을 활용하여, $\mathbf{N}^{\dagger}\mathbf{N}$ 역시 convolution들의 block matrix일 뿐임을 알 수 있습니다.

흔히 $(f \ast g) (x, y) = \sum _ {z, w} f(z, w) g(x - z, y - w)$와는 다르게, cross-correlation $(f \star g)(x, y) = \sum _ {z, w} f(z, w) g(x + z, y + w)$를 정의하자. convolution이 더 깔끔한 연산이지만, 구현에 있어서는 cross-correlation이 더 많이 사용된다. kernel size가 $w _ {d}$인 cross-correlation operator들의 공간을 $\mathrm{Conv2d}(w _ {d})$로 쓰자. Linear operator $A \in \mathrm{Conv2d}(w _ {d})$에 대해 $A$를 kernel로 보았을 때의 $w _ {d} \times w _ {d}$의 배열을 $K(A)$로 쓴다.

편의상 $K$를 원점에 대칭한 새로운 kernel을 $\text{flip}(K)$라고 하자.

Linear operator $A \in \mathrm{Conv2d}(w _ {d})$에 대해, $A^{\dagger} \in \mathrm{Conv2d}(w _ {d})$이고 $K(A^{\dagger}) = \text{flip}(K(A))^{*}$가 성립한다.

$A, B \in \mathrm{Conv2d}(w _ {d})$에 대해 $AB \in \mathrm{Conv2d}(2w _ {d} - 1)$이고, $K(AB) = \mathrm{flip}(K(A)) \star K(B)$가 성립한다.

따라서, $\mathbf{D} _ {ij} = \sum _ {k = 1}^{r} K(\mathbf{N} _ {ik})^{*} \star K(\mathbf{N} _ {kj})$가 됩니다. $\mathbf{D} _ {ij}$를 미리 구해두면 매 iteration마다 $N _ {c}^{2}$개의 convolution만 쓰고도 문제를 해결할 수 있습니다.

Auto-Calibration: acquiring the nulling kernel

이제 Nulling weight $\tilde{\mathbf{n}} _ {1}, \cdots, \tilde{\mathbf{n}} _ {r} \in \mathbb{C}(N _ {c}w _ {d}^{2})$를 얻는 방법만 생각하면 됩니다. 이는 $\tilde{\mathbf{S}^{\dagger}}$의 null space에서 얻어지겠지만, 우리는 sensitivity kernel을 모르니까 대신 $\tilde{\mathbf{n}} _ {i}^{\dagger} \tilde{\mathbf{d}} = 0$을 이용합시다.GRAPPA나 PRUNO를 이용한 데이터를 얻을 때, K-space의 center를 중심으로 $N _ {b} \geq 2w _ {d} $ 개 정도의 phase encoding line을 undersample하지 않고 얻습니다. 이러한 phase encoding line을 ACS (auto-calibrating section)이라고 부릅니다.

앞서 기술하였듯 $\tilde{\mathbf{S}}^{\dagger}$가 K-space position과 무관하므로, $\tilde{\mathbf{n}} _ {i}$ 또한 그렇습니다. 즉, local data point $\tilde{\mathbf{d}}$를 어느 point에서 얻든 간에 $\tilde{\mathbf{n}} _ {i}^{\dagger}\tilde{\mathbf{d}} = 0$은 성립합니다. 따라서 ACS line에서 얻을 수 있는 모든 $L$개의 data point를 긁어모아 Calibration matrix $\tilde{\mathbf{D}} \in \mathbb{C}(nw _ {d}^{2}, L)$을 만들면, $\tilde{\mathbf{D}}$의 null space에서 nulling kernel을 얻을 수 있습니다.

다만 실제 데이터 상에선 여러 오차가 있기 때문에, $\tilde{\mathbf{D}}$의 singular-value decomposition을 통해 가장 작은 $r$개의 singular value를 주는 eigenvector를 nulling weight로 사용합니다.

Conclusion

이렇게 오늘은 MR imaging이라는, frequency domain (K-space) 에서 데이터를 추출하여 이미지를 만드는 특이한 이미지 가공에 대해 알아보았습니다. 흔히 imaging에서는 resolution이나 SNR 등 노이즈를 잡는 데 주로 신경을 쓰지만, MR imaging에서는 이외에도 aliasing이라는 특이한 현상이 발생하는 것도 확인해보았고, 이를 보정하기 위한 몇 가지 방법론을 알아보았습니다.

오늘 알아본 PRUNO의 경우 GRAPPA에 비해 성능 면에서 굉장히 뛰어나고, undersample factor $R$이 클 때도 robust한 모습을 보이는 좋은 알고리즘이지만, 속도 문제로 대부분의 MR 장비에서는 SENSE나 GRAPPA를 사용하고 있습니다.

또한 Parallel imaging을 수행했다고 모든 문제가 끝난 것이 아닙니다. 당장 얻은 데이터 수가 적기 때문에, Parallel imaging을 통해 복원한 이미지는 원본 이미지에 비해 훨씬 noisy합니다. 또한 코일들이 “ideal configuration”을 이루고 있다는 가정 자체도 충분한 검증을 거치지 않으면 사용할 수 없기에, real world problem에는 훨씬 다양한 문제와 다양한 방법론이 있습니다.

소스 코드는 추후 적절한 가공을 거쳐 공개하도록 하겠습니다.

Reference

mriquestions
Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J Magn Reson Imaging 2012;36:55-72. (review)
Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999 Nov;42(5):952-62. PMID: 10542355.
Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002 Jun;47(6):1202-10. doi: 10.1002/mrm.10171. PMID: 12111967.
Zhang J, Liu C, Moseley ME. Parallel reconstruction using null operations. Magn Reson Med. 2011 Nov;66(5):1241-53. doi: 10.1002/mrm.22899. Epub 2011 May 20. PMID: 21604290; PMCID: PMC3162069.