Wireless Digital Communication 6
서론
지난 글에서는 OFDM이란 무엇인지, 또 OFDM과 FFT/IFFT 와는 어떤 관계가 있는 지에 대해 알아보았습니다.
제가 처음 글에서 OFDM이라는 시스템은 ISI를 줄이기 위해 고안한 시스템이라는 설명을 했었습니다. 과연 어떤 방식으로 ISI를 줄이는 지 설명하고, OFDM의 전체적인 구조를 설명한 뒤에 글을 마치겠습니다.
이 글이 해당 시리즈의 마지막 글이 될 예정입니다. 마지막까지 잘 따라와주시면 감사하겠습니다.
본론
지난 글에서는 채널이 없다고 가정을 하였고, 따라서 ISI에 대한 생각은 하지 않아도 됐습니다. 하지만 실제로는 모든 신호는 어떤 특정한 채널을 거치게 되고 이를 그림으로 표현하면 다음과 같습니다.

위 도식의 결과는 $y(t) = \sum_k d_k h(t-kT) + n(t)$가 됩니다. 아래 그림의 오른쪽 함수를 $h(t)$라 한다면 $y(t)$의 그림은 왼쪽과 같을 것입니다. (물론 크기나 부호는 제 마음대로 설정했습니다.)

ISI는 신호 간 간섭을 의미합니다. 과연 어떤 상황에서 이 ISI가 존재할까요?
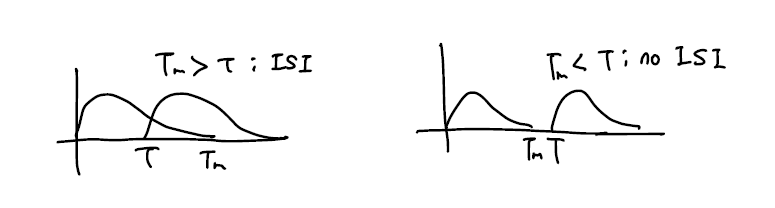
위의 그림에서 알 수 있듯이 $T_m > T$ 이면 ISI가 발생하고 그렇지 않다면 ISI는 발생하지 않습니다. 참고로 통신이 4G, 5G로 갈수록 data rate이 증가하는데, 이는 $R = \frac{b}{T}$로 세대가 지날수록 $T$가 감소하므로 ISI가 더 크게 발생합니다.
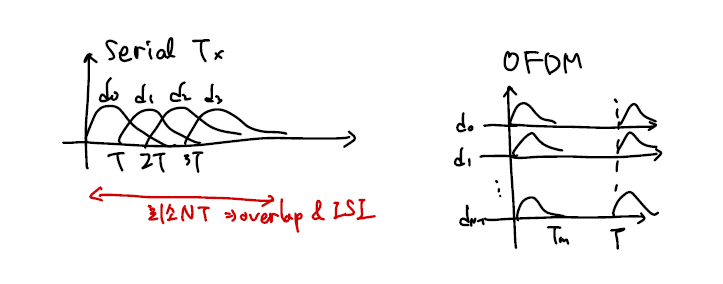
이를 해결하기 위해 OFDM은 신호를 병렬로 처리합니다. 위 그림에서 볼 수 있듯이 각 채널에서 ISI는 발생하지 않습니다. 대신에 위 방식대로 하면 캐리어 간 간섭인 ICI(Inter Carrier Interference)가 발생하게 됩니다. 어떻게 ISI는 없앴는데 이제는 새로운 숙제인 ICI를 없애는 방법을 생각해야합니다. 이 역시 캐리어 간의 신호를 전부 orthogonal하게 만듦으로써 해결할 수 있습니다.
Guard time
Guard time이란, 심볼 간 간섭을 없애기 위해 심볼과 심볼 사이에 아무런 신호도 없는 구간을 추가하는 것을 말합니다. 두 개의 신호가 짧은 간격으로 보내진다면 간섭이 더 크게 일어나지만 긴 간격으로 보내면 간섭이 약해지는 효과를 얻을 수 있기 때문에 해당 구간을 넣는 것입니다. 지금부터 다양한 guard time의 유형과 그에 대한 ISI와 ICI를 분석해보겠습니다.
첫 번째로 channel delay와 guard time이 없는 상태, 즉 $h(t) = \delta(t)$를 만족하는 상태를 생각해봅시다.
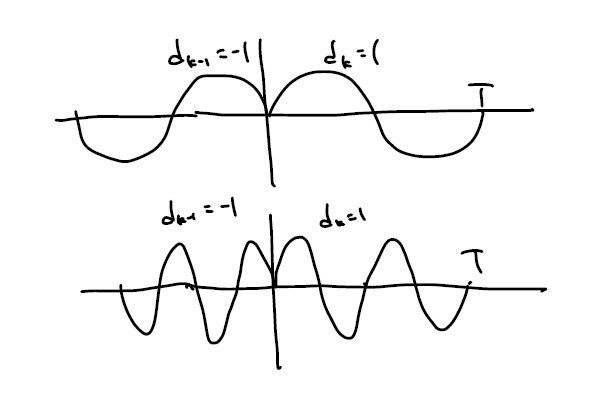
위 그림에서 심볼 간 간섭은 당연히 없을테고, 캐리어 간 간섭 역시 두 심볼이 orthogonal 하기 때문에 없습니다. 이는 지난 글에서 구간 T 동안 정수 개의 cycle을 갖는 sinusoid들은 전부 orthogonal 하다는 것을 증명했기 때문에 자명합니다.
하지만 실제로는 channel delay가 존재하기 때문에 guard time은 없지만 channel delay가 있는 상태, 즉 $h(t) = \delta(t) + a\delta(t-T_m)$ 을 만족하는 상태를 생각해봅시다.

두 서브 캐리어에서 파란색으로 그려진 부분은 channel delay에 의한 심볼입니다. 그 중에서 붉은 형광펜으로 칠해진 부분을 살펴보면, 이는 이전 심볼이 딜레이되어 현재 심볼에 영향을 주기 때문에 ISI가 발생합니다. 또한 검정색으로 그려진 심볼(원래 심볼)과 파란색으로 그려진 심볼은 서로 다른 캐리어 상에서 orthogonal하지 않기 때문에 ICI가 생깁니다.
다음으로는 ISI를 없애기 위해 아래 그림과 같이 zero-padding guard time을 추가해볼 겁니다.

channel delay를 $T_m$, guard time을 $T_g$라 했을 때, $T_m < T_g$이면 ISI는 발생하지 않습니다. 하지만 두 캐리어 간 검은색 심볼과 파란색 심볼은 앞에서와 마찬가지로 orthogonal하지 않기 때문에 ICI가 생깁니다. 따라서 우리는 zero-padding guard time이 아닌 다른 방식을 찾아야합니다.
그래서 나온 방식이 cyclic prefix이고, 실제 OFDM은 이 기법을 이용합니다.

위 그림처럼 기존에는 guard time에 zero-padding을 했다면, 이번에는 해당 심볼의 뒷부분에 해당하는 부분을 guard time에 채워주는 겁니다. 그렇게 된다면 zero-padding일 때와 마찬가지로 심볼 간에는 서로 영향을 주지 않기 때문에 ISI는 발생하지 않고, 두 캐리어 간 심볼들은 orthogonal하기 때문에 ICI 역시 발생하지 않습니다. 그림만 보면 ISI가 발생할 수 있다고 생각할 수도 있지만, 간섭이 생기는 부분은 guard time 구간으로 실제 신호 처리에서 버려지는 부분이므로 무시해도 됩니다.
다시 본론으로 돌아와서 어떤 변조된 신호 $s_{bb}(t)$가 채널 $h(t)$를 지난다고 해봅시다. 노이즈가 없는 채널에서의 결과는 $r(t) = s_{bb}(t) \ast h(t)$가 될 것입니다.

m 번째 demodulator의 도식은 위와 같고, 이를 수식으로 정리하면 다음과 같습니다.
$ \hat{d_m} = \frac{1}{T} \int_0^T r(t) e^{-j2 \pi m \Delta ft} dt $
$ = \frac{1}{T} \int_0^T \int_{-\infty}^{\infty} s_{bb}(t - \tau )h( \tau ) d \tau e^{-j2 \pi m \Delta ft} dt$
$ = \frac{1}{T} \int_0^T \int_{-\infty}^{\infty} \sum_{k=0}^{N-1} d_k e^{j2 \pi k \Delta f(t- \tau )} h( \tau ) d \tau e^{-j2 \pi m \Delta ft} dt$
$ = \frac{1}{T} \sum_{k=0}^{N-1} d_k \int_{-\infty}^{\infty} h( \tau ) e^{-j2 \pi k \Delta ft} \int_0^T e^{j2 \pi \Delta f(k-m)t}$
여기서 $\int_{-\infty}^{\infty} h( \tau ) e^{-j2 \pi k \Delta ft}$ 는 $h( \tau )$ 의 푸리에 변환인 $H(f) = \int_{-\infty}^{\infty} h( \tau ) e^{-j2 \pi ft}$ 를 $f=k \Delta f$ 에 대해 샘플링한 것이고, $\int_0^T e^{j2 \pi \Delta f(k-m)t}$ 는 $T \delta_{k-m}$ 이므로
$ = \frac{1}{T} \sum_{k=0}^{N-1} d_k H(f) \vert_{f=k \Delta f} \cdot T \delta_{k-m}$
$ = d_m H(f) \vert_{f = m \Delta f} = d_m H_m$ 이 된다.
여기서 $H_m$ 은 $h(t)$를 푸리에 변환했을 때, $f = m \Delta f = \frac{m}{T}$에서 샘플링한 결과값입니다.
실제로 $d_m$은 complex signal이지만, 편의상 frequency domain에서의 정보라고 생각하겠습니다. (그래야 $H_m$과 곱해지는 것이 말이 됩니다.)
위로부터 얻은 결론이 무엇이냐하면, 수신단이 채널 함수 $h(t)$를 알고 있다면, $\hat{d_m}$을 통해 $d_m$을 구할 수 있다는 점입니다. 단순히 $\hat{d_m}$에 $\frac{1}{H_m}$을 곱해주면 됩니다. 그리고 실제로 channel estimation을 통해서 수신단에서는 채널 함수가 무엇인지 알 수 있습니다. 송신단, 수신단 모두가 알고 있는 pilot 신호 $d_k$를 보내면 됩니다. 수신단은 $\hat{d_k}$를 수신하고, $d_k$를 알고 있으니 $H_k$ 역시 알 수 있고 이를 통해 $h(t)$를 역산할 수 있습니다.
discrete-time case
잠시 이산신호에 대한 이야기를 하고 넘어가겠습니다. 길이가 $N$ 인 두 수열 $x[n]$과 $h[n]$이 있을 때 둘의 circular convolution은 DFT와 다음과 같은 dual 관계에 있습니다.
$ x[n] \circledast h[n] \Leftrightarrow X[k] H[k] $. 여기서 $X[k]$는 $x[n]$의 DFT입니다. OFDM 과정에서 우리가 원하는 것은 이 circular convolution의 결과입니다. 우리는 이와 같은 결과를 circular convolution 없이 cyclic prefix를 통해서도 구할 수 있습니다.
예를 들어 $x[n] = { 1, 2, 3, 4, 5, 6 }, h[n] = { 1, 1, 1, 0, 0, 0 }$이라고 해보겠습니다. 이 때 $x[n] \circledast h[n] = { 12, 9, 6, 9, 12, 15 }$입니다. $x[n]$에 길이 2짜리 cyclic prefix를 추가한 배열을 $\tilde{x}[n]$이라고 해봅시다. 그러면 $\tilde{x}[n] = { 5, 6, 1, 2, 3, 4, 5, 6 }$이 됩니다. 이를 $h[n]$과 linear convolution한 결과는 $\tilde{x}[n] \ast h[n] = { 5, 11, 12, 9, 6, 9, 12, 15, 11, 6}$이 되는데, 양 끝 2개를 제외한 가운데 6개는 circular convolution과 결과가 같습니다. 본 예제에서 cyclic prefix의 길이가 2인 이유는 $h[n]$의 길이가 3(0은 제외)이기 때문이고, 보통 $h[n]$의 길이에서 1을 뺀 값으로 설정합니다. 그 이유는 단순히 $h[n]$의 길이가 $ \nu $일 때, cyclic prefix의 길이를 $ \nu - 1$ 이상으로 해야 circular convolution의 결과를 얻을 수 있기 때문입니다.
OFDM
$ { s_n^i } $를 $n$ 번째 subcarrier 에서의 $i$ 번째 OFDM 심볼이라고 해봅시다. 그리고 해당 신호가 통과하는 채널의 길이를 $\nu + 1$ 이라고 가정하면 $ \tilde{s_n}^i $는 $s_n^i$에 길이 $\nu$의 cyclic prefix를 추가하는 것입니다. 이를 그림으로 표현하면 다음과 같습니다.

이 $\tilde{s_n}$을 $h[n]$과 linear convolution을 적용하면 해당 carrier의 output $\tilde{y_n}$이 다음과 같은 형태로 나옵니다.
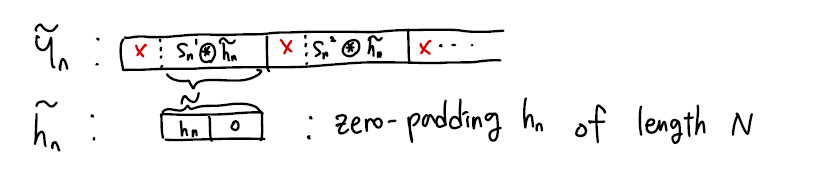
위 그림에서 x 표시는 쓰레기 값으로 $s_n^i$에서 생성된 쓰레기 값과 $s_n^{i+1}$에서 생성된 쓰레기 값은 같은 곳에 겹치게 됩니다만 추후에 이들을 싹 없애는 작업을 할 것이기 때문에 크게 신경쓰지 않아도 됩니다. 그렇게 없애고 나면 다음과 같이 깔끔한 결과가 나옵니다.
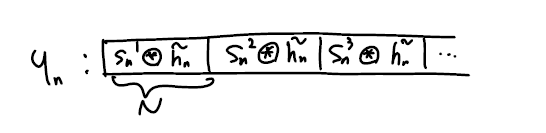
$i$ 번째 블럭의 결과를 $y_n^i$라고 하면, 이를 DFT 해서 $Y_k^i = DFT { y_n^i } = DFT { s_n^i \circledast \tilde{h_n} } = DFT { s_n^i } \cdot DFT { \tilde{h_n} }$ 를 얻을 수 있습니다.
마지막으로 $H_k = DFT { \tilde{h_n} }$을 통해 우리가 구하고 싶은 원본 $d_k^i$는 $DFT { s_n^i } = \frac {Y_k^i}{H_k} $을 통해 구할 수 있습니다. 즉, $s_n = IDFT { d_k }$입니다.
지금까지 한 내용들을 바탕으로 OFDM의 시스템을 모델링하면 다음과 같습니다.

실제로는 error의 확률을 줄이기 위해 channel coding이나 interleaving 기법들을 사용하지만 본 글에서는 생략하겠습니다.
결론
본 글에서는 ISI, ICI를 줄이기 위해 사용하는 여러가지 guard time들과 실제 OFDM에서 사용하는 cyclic prefix 기법에 대해 다뤘습니다.
본 글을 마지막으로 6개의 글에 걸쳐 무선 통신 시스템에 대한 간단한 설명을 해보았습니다.
통신에 관심이 있는 분들이 가볍게 읽고 갔으면 좋겠다는 바람을 마지막으로 글을 마치겠습니다.
Reference
- Fundamentals of Communication Systems, John G Proakis