알고리즘 문제 접근 과정 8
알고리즘 문제 접근 과정 8
이번 포스트에서도 ‘알고리즘 문제 접근 방법’ 시리즈에서 진행했듯이 특정 문제를 해결하기 위해 가장 낮은 단계의 접근에서부터 최종 해법까지 해결해나가는 과정을 작성합니다.
최대한 다양한 유형의 문제들을 다루어, 많은 문제 유형에서의 접근 방법에 대한 실마리를 드리는 역할을 하려 합니다.
버스 노선 - KOI 2014 고등부 2번
풀이
이 문제를 해결하는데 큰 어려움이 되는 부분은 구간이 원형으로 되어있다는 점일 것입니다. 그렇다면 일단, 문제가 원형으로 생겨있지 않고 0번을 기준으로 일직선으로 생긴 형태라면 어떻게 해결할 수 있을까요?
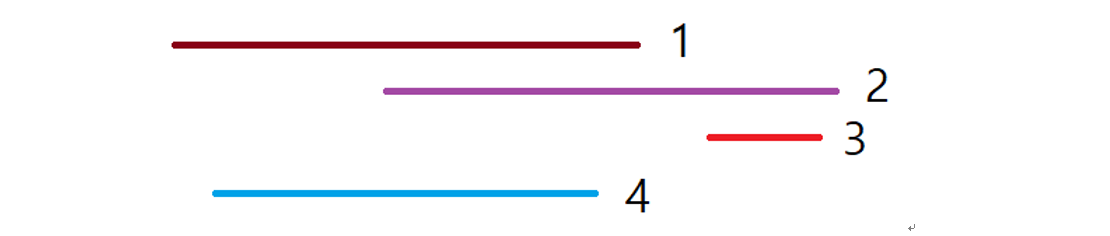
간단히, 위와 같이 생긴 일직선 구간들로만 이루어진 노선들이 존재할 경우, 특정 구간이 다른 구간에 포함된다는 것을 어떻게 찾을 수 있을까요? 가장 쉬운 방법으로는, 한 구간을 잡고 다른 모든 구간에 대해 비교하면서 현 구간을 포함하는 다른 구간이 있는지 확인하는 것으로 해결할 수 있습니다. 이 방법으로는 $O(N^2)$에 해결할 수 있지만, 노선의 수가 많을 경우 충분히 빠르게 동작하지 않을 수 있습니다. 그렇다면, 어떻게 더 빠르게 해결할 수 있을까요?
주어진 노선들을 시작점이 빠른 순서대로 정렬해줍시다.
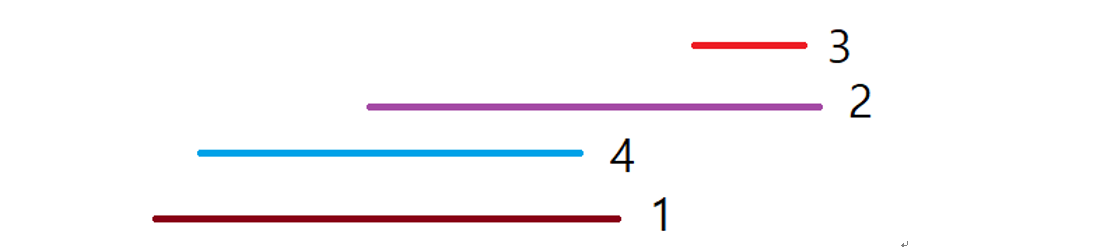
위와 같이 정렬하고 나면, 우리는 노선을 앞에서부터 순서대로 볼 때에 뒤에 나오는 노선의 시작점은 항상 앞에 나온 노선들보다 늦고, 그 뒤에 나올 노선들보다는 항상 빠르다는 것을 알 수 있습니다. 즉, 특정 노선이 포함되기 위해서는 시작점과 끝점 모두가 포함되어야 하므로, 순서대로 진행할 때 현재 우리가 보고있는 노선을 포함할 수 있는 노선은 항상 앞에나온 노선 중에 있거나 혹은 존재하지 않는다는 것을 알 수 있습니다.
- ex) 4번 노선은 시작점이 늦는 2번이나 3번은 아무리 끝점이 길어도 포함 불가
이를 통해 순서대로 진행하면서 현재까지 나온 노선들 중 끝 구간의 번호가 가장 큰 값을 저장하고 있으면, 이후에 나오는 노선의 끝 구간이 더 작을 경우 항상 포함하는 노선이 존재함을 알 수 있어 특정 노선이 취소되는지 여부를 바로 확인할 수 있습니다. 여기에서 시작점이 같을 경우에 문제가 생길 수 있지 않은지 생각해볼 필요가 있습니다. 시작점이 같은 때에는 끝 지점을 모르는 상태에서 누가 누구를 포함할지 알 수 없기 때문에 꼭 시작점 순서대로 포함이 되는 것이 아닐 수 있습니다. 하지만 여기서, 시작 구간이 같을 경우 끝 구간이 늦은 쪽이 항상 다른 모든 같은 시작구간인 노선을 포함할 수 있다는 것을 이용해 시작이 같을 경우 끝이 늦는 노선이 먼저 오도록 정렬을 해주면 이 문제를 해결할 수 있습니다.
이를 통해 모든 경우에 대해 항상 특정 노선이 포함되는지 여부를 알 수 있으며, 모든 과정은 정렬을 하는 때에 가장 많은 시간이 들어 총 $O(NlgN)$에 해결할 수 있습니다.
하지만 아직 우린 원형일 때의 문제를 해결하지 못했다. 혹시 문제를 잘 변형하는 것으로 선형일 때 해결한 방법을 원형에도 적용할 수 있을까요?
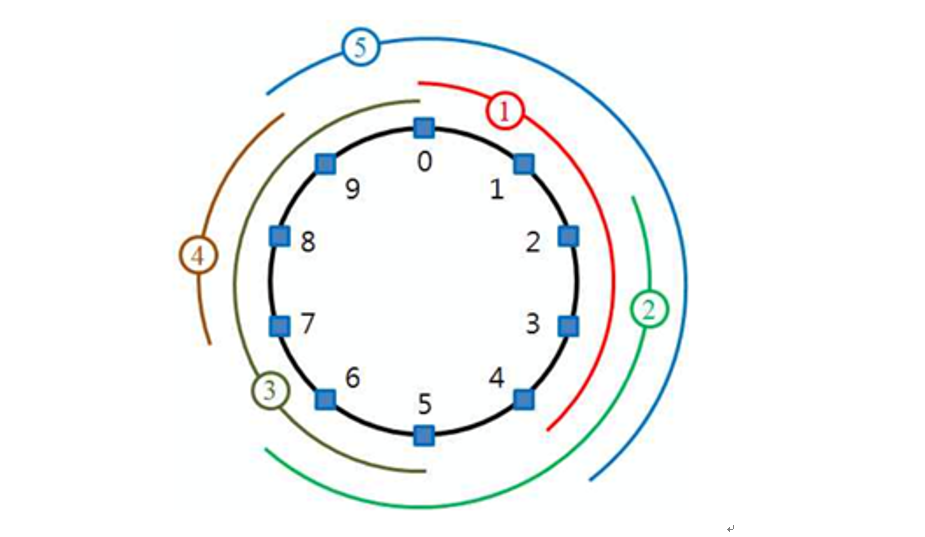
예시 그림을 한 번 살펴봅시다.
위 그림에서 5번 노선은 $[9, 4]$인 형태로 주어지며, 1번 노선 $[0, 4]$를 포함하있고, 3번 노선은 $[5, 0]$ 형태로 주어지며 4번 노선 $[7, 9]$를 포함하고 있습니다.
이 때, $[9, 4]$, $[5, 0]$은 표현하기 어렵기 때문에, 구간을 한 바퀴 더 있다고 생각하고(즉, 0은 10, 1은 11, 2는 12와 같도록) 바꿔주게 되면 $[9, 4]$는 $[9, 14]$, $[5, 0]$은 $[5, 10]$으로 바뀌게 됩니다.
이렇게 바꾸고 나면 4번 구간 $[7, 9]$는 3번 구간 $[5, 10]$에 포함되게 되지만, 1번과 5번 노선은 아직 포함 관계가 없습니다. 이 때, (0은 10)과 (4는 14)와 같다는 것을 이용해 $[0, 4]$를 $[10, 14]$로 바꿔주게되면 어떻게 될까요? 이는 5번 구간인 $[9, 14]$에 완전히 포함되게 됩니다. 즉 우리는 현재 구간을 2배 하고 대응되는 i번 정류장을 $N + i$번을 만드는 것으로 문제를 해결할 수 있습니다.
그렇다면, 이는 모든 구간에 대해서도 변함이 없을까요?
이러한 구간들이 생길 수 있는 모든 예시를 통해 포함관계에 문제가 생기는지 확인해봅시다.
위 그림과 같이 모든 경우에도 포함관계가 변하지 않는데, 이는 포함시킬 수 있는 경우가 변하지 않기 때문입니다. n을 더하기 전의 노선과 n을 더한 이후의 노선은 항상 길이가 n만큼 차이가 나지만, 노선들은 최대 길이가 n이기 때문에, 양 쪽에 n을 더하기 전의 구간과 더한 이후의 구간 둘 다에 포함 되는 경우는 존재하지 않습니다. 즉, 어떻게 존재하게 되든 새로 추가한 노선은 추가하기 전의 노선과 서로 연관되는 경우가 없어 n을 더하기 전의 노선에 일부만 포함되는 구간은 더한 이후의 노선에서 전체가 포함되는 경우는 존재하지 않습니다.
즉, 이러한 과정은 0을 걸치는 노선을 표현하는 방식으로의 역할만 하게 되므로 실제 결과에 영향을 주지 않습니다.
이를 통해, 우리는 선형일 때의 알고리즘을 그대로 정류장을 $2N$으로 늘린 상태에서의 노선을 고려하는 것으로 해결 가능합니다. 이 때, 특정 구간의 번호가 포함되는 경우가 있는지를 확인해주기만 하면 같은 시간복잡도인 $O(NlgN)$에 문제를 풀 수 있습니다.
햄버거 분배 - KOI 2020 1차 대회 고등부 2번
관찰
주어진 문제를 해결할 수 있는 가장 쉬운 방법을 생각해봅시다.
우리는 햄버거와 사람의 위치, 인접한 햄버거를 먹을 수 있는 반경 K가 주어집니다. 결국, 우리는 매 사람과 햄버거들이 자신과 연결될 수 있는 반경 내에 있는 집합들을 구해줄 수 있고, 이들 중 최대로 연결할 수 있는 때 연결의 수를 구하면 됩니다.
만약 주어진 문제에서 i명의 사람과 j개의 햄버거가 존재한다고 합시다. 이 때, 우리는 i명의 사람과 j개의 햄버거를 모두 매치시켜보는 방법을 생각해볼 수 있습니다. 즉 모든 가능한 매치 중, 실제로 연결이 가능한 햄버거와 사람의 수를 세서, 이들 중 최댓값을 이용하여 답을 구해낼 수 있습니다.
일반성을 잃지 않고 i >= j라 가정할 때, 가능한 매치의 수는 ${i}P{j}$ 가 되므로, 이들 연결을 모두 해보는 것으로도 문제를 해결할 수는 있습니다. 허나 순열의 경우, 수가 커지면 기하급수적으로 증가하므로, n이 증가할 때에 문제를 해결하기 어려울 수 있습니다.
풀이
우리가 어떤 문제에 접근할 때에는, 무언가를 시작하는 대상이 무엇인가부터 접근해보는 것이 상당히 많은 경우에 좋은 영감을 줄 수 있습니다.
앞선 문제에서 가장 해결하기 힘들었던 부분은 바로 어떤 햄버거와 어떤 사람을 연결할 것인가? 에 관한 문제였습니다. 모든 사람과 햄버거에 대해서 생각해보니 너무나도 많은 시간이 걸리게 되므로, 우리는 특별한 방법으로 햄버거와 사람을 연결시켜줄 방법을 찾아야합니다.
이를 해결하기 위해, 우리는 한 번 ‘처음으로 햄버거와 사람이 연결되는 상황’을 생각해볼 수 있습니다.
식탁의 가장 앞에 놓여있는 햄버거를 기준으로 한 번 생각해봅시다.
가장 앞에 놓인 햄버거를 먹을 수 있는 사람들이 식탁의 앞쪽에 가까운 순서대로 a, b, c, d 세 사람이라고 합시다. 이 때, 어떤 사람이 햄버거를 먹어야 가장 좋은 연결이라고 볼 수 있을까요?
굳이 햄버거와 사람을 연결할 수 있는데 연결하지 않는 것은 좋지 않다는 것을 쉽게 알 수 있습니다. 만약 a, b, c, d 모두 다른 햄버거와 연결해서 최대 사람 수를 만들 수 있다면, 우리는 그 중 a, b, c, d 와 연결된 한 쌍을 현재 햄버거와 교체해도, 최대 사람 수 자체는 변하지 않아 적어도 같은 결과를 만들 수 있기 때문입니다. 즉, 우리는 적어도 이들 중 한 명과 매칭하는 것은 사람 수를 최대로 만들기 위해 필요한 것임을 알 수 있습니다.
그렇다면 이 중 어떤 사람과 연결해야 좋은 결과를 얻을 수 있을까요? 이는 앞선 문제에서, 햄버거와 사람이 K 이하의 반경에 있는 경우에만 연결할 수 있다는 것을 이용하여 좋은 접근을 얻을 수 있습니다.
이를 해결하기 위해, 첫 햄버거 다음에 있는 햄버거들이, a, b, c, d 후보 중 어떤 사람들을 연결할 수 있는지 생각해봅시다.
- 어떤 햄버거가 a와 연결할 수 있다면, 그 햄버거는 b, c, d 또한 연결할 수 있습니다. 현재 우리가 보는 햄버거가 가장 앞에 있는 햄버거이기 때문에, 이 뒤에 있는 햄버거의 왼쪽 반경이 a를 커버하고 있다면, b, c, d 또한 커버할 수 있습니다.
- 어떤 햄버거가 a와 연결 불가하고, b를 연결할 수 있다면, 앞선 방식처럼 생각하여 그 햄버거가 c, d 또한 연결할 수 있음을 알 수 있습니다.
- 어떤 햄버거가 a, b와 연결 불가하고 c를 연결할 수 있다면, d 또한 연결할 수 있습니다.
- 어떤 햄버거가 d만 연결할 수 있을 수 있습니다.
- 어떤 햄버거가 a, b, c, d 모두가 연결 불가능할 수 있습니다.
이 중, 5번의 경우, 우리가 첫 햄버거를 어떤 사람과 연결하더라도 이후의 연결에 영향이 없습니다.
이를 제외한 나머지 경우들을 살펴봅시다.
우리는 여기에서, d는 1, 2, 3, 4번에 해당하는 햄버거들과 모두 연결이 될 수 있으며, c는 1, 2, 3번, b는 1, 2번, a는 1번의 경우에 해당하는 햄버거들과만 연결될 수 있음을 알 수 있습니다.
우리는 현재 햄버거에서의 연결이, 이후에 나오는 다른 햄버거들의 연결 후보를 줄일 수 있기 때문에 문제가 되었습니다. 허나 이렇게 연결관계를 살펴보게 되면, d를 선택하여 연결할 경우, a, b, c를 선택할 때보다 항상 더 같거나 많은 연결 후보를 줄이게 되며, c를 선택할 경우 a, b, b를 선택할 경우 a를 선택할 때보다 항상 더 많은 연결 후보를 줄이게 된다는 것을 알 수 있습니다. 이들은 모두 포함 관계이기 때문에, 항상 a < b < c < d 순으로 더 많은 후보를 줄인다는 것을 알 수 있습니다.
즉, 우리는 4명의 매치 가능한 사람 후보가 있을 때, 앞으로의 연결에서 후보를 적게 줄이기 위해서는 항상 첫 번째 햄버거가 연결 가능한 사람 중, 식탁의 시작에 가장 가까운 위치에 있는 사람인 a와 연결하는 것이 가장 좋다는 것을 알 수 있었습니다. 이는 4명을 더 많은 후보로 확장하거나 줄여도 항상 성립한다는 것을 어렵지 않게 보일 수 있습니다.
이렇게 첫 번째 햄버거의 연결을 하나 확인할 수 있었습니다. 그렇다면 나머지 햄버거의 연결은 어떻게 될까요?
우리가 첫 햄버거의 연결을 무조건 고정시키게 되면, 해당 햄버거와 사람은 모든 후보에서 제거된 상태로 볼 수 있습니다. 그렇다면 이 때에 남은 햄버거 중 가장 앞에 있는 햄버거에서 시작한다면, 우리는 이를 다시 첫 햄버거로 보고 문제를 접근할 수 있습니다.
결국 이 문제를 매 순간마다 가장 앞에 있는 햄버거를 매치시키는 문제로 본다면, 항상 가능한 후보들 중 가장 앞에 있는 사람을 매치시켜주는 방법이 항상 최선이라는 것을 알 수 있게 됩니다.
이를 매 햄버거마다 앞에 있는 사람을 매치시키는 방법으로 구현하면 최대 햄버거 $O(N)$, 사람 수 $O(N)$이므로 총 $O(N^2)$에 해결할 수 있습니다.
허나 우리는 앞선 방법으로 매 순간 가장 앞에 있는 햄버거와, 그 햄버거와 연결할 수 있는 가장 앞에 있는 사람만이 중요함을 알게 되었으므로, 매 상태에서 가장 앞에 있는 햄버거와 사람의 위치를 기록하는 두 개의 포인터(two pointer)를 이용하면, $O(N)$에 해결할 수 있습니다.
코드
버스 노선
#include <bits/stdc++.h>
using namespace std;
struct Data{ int x, y, idx; } arr[2000010];
int n, m, cnt;
int carr[500010];
bool compare(Data d1, Data d2){
if(d1.x == d2.x) return d1.y > d2.y;
return d1.x < d2.x;
}
int main(){
int i, now;
scanf("%d %d",&n, &m);
for(i = 0; i < m; i++){
scanf("%d %d",&arr[cnt].x, &arr[cnt].y);
arr[cnt].idx = i + 1;
if(arr[cnt].x > arr[cnt].y){
arr[cnt].y += n;
cnt++;
}
else{
arr[cnt + 1].x = arr[cnt].x + n;
arr[cnt + 1].y = arr[cnt].y + n;
arr[cnt + 1].idx = i + 1;
cnt += 2;
}
}
sort(arr,arr+cnt,compare);
now = arr[0].y;
for(i = 1; i < cnt; i++){
if(arr[i].y <= now) carr[arr[i].idx] = 1;
now = max(arr[i].y, now);
}
cnt = 0;
for(i = 1; i <= m; i++){
if(!carr[i]) printf("%d ", i);
}
return 0;
}
햄버거 분배
#include <bits/stdc++.h>
using namespace std;
int n, k, res;
char arr[20010];
int main(){
int i = 0, j = 0;
scanf("%d %d %s", &n, &k, arr);
while(i < n){
while(j < i - k) j++;
if(arr[i] == 'P'){
while(j <= i + k && j < n){
if(arr[j] == 'H'){ res++, j++; break; }
j++;
}
}
i++;
}
printf("%d", res);
return 0;
}