USACO 활용하여 문제 풀어보기

서론

USACO란 미국의 정보올림피아드로, 어렵지 않은 알고리즘을 이용하여 문제를 출제됩니다. 학생들은 등급별로 3개의 문제를 풀며 Bronze부터 Platinum 까지 승급하며 올라가는 방식입니다. 이번에는 2021년 12월에 진행되었던 USACO Silver, Gold 시험의 1번문제의 풀이를 하려 합니다.

Closest Cow Wins (USACO Silver #1)

이 문제는 $K$개의 풀밭이 각각 $p_i$ 위치에 $t_i$의 맛을 가지고 있습니다. Nhoj와 John은 소를 배치하는데, 각 풀밭은 가까이에 있는 소에게 먹히게 됩니다. Nhoj의 소와 John의 소가 풀밭에서 같은 거리에 있을 때에는, Nhoj의 소가 먼저 먹게 됩니다. Nhoj는 소 $M$마리를 미리 $f_i$에 배정한 상태일 때, John이 $N$마리의 소를 배정하여 먹게되는 풀밭의 맛의 합이 가장 크게 될 때의 그 값을 구하는 문제입니다.

이 문제는 Nhoj가 미리 소를 배정해 놓았기 때문에, 그에 맞추어 John이 소를 Greedy하게 배정해야 합니다. John이 놓는 소는 좌우로 인접한 Nhoj의 소와 경쟁하기 때문에, Nhoj의 소들을 기준으로 구간을 나누어 관찰할 수 있습니다.

Nhoj의 소들을 기준으로 구간을 나누어서 탐색해보면, 중요한 점은 두 가지를 알 수 있습니다.

Nhoj의 소들이 만들어낸 구간 $p_i$ ~ $p_{i+1}$ 에서 한 마리의 소는 풀밭끼리 $(p_{i+1}-p_i)/2$ 이상의 차이가 나는 것은 먹지 못한다
한 구간에 소는 2마리만 넣어도 충분하다

John이 $p_i$, $p_{i+1}$ 사이에 놓은 소가 $(p_{i+1}-p_i)/2$ 이상 차이나는 풀밭을 먹지 못하는 이유는, John의 소는 각각 $p_i$, $p_{i+1}$ 에 있는 소와 정중앙에 있는 풀밭까지만 먹을 수 있기 때문입니다. 풀밭 기준으로는 가까이에 있는 소들에게 먹히기 때문에, 최대 절반까지만 먹히게 됩니다.

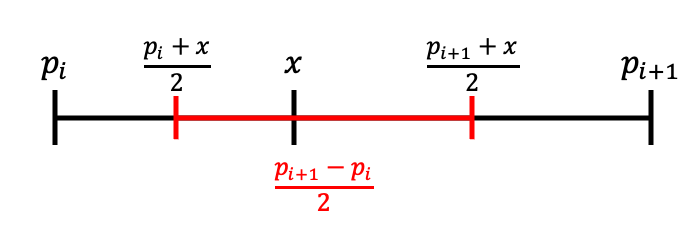
위 그림을 통해 조금 더 명료하게 알 수 있습니다.

그리고, Nhoj의 소들 사이에서는 단 두 마리로 모든 풀밭을 먹을 수 있습니다. 간단하게, $p_i+0.5$, $p_{i+1}-0.5$ 두 위치에 John이 소를 위치시킬 경우 구간에 있는 모든 풀밭을 John의 소가 먹게 되는 것은 자명하게 알 수 있습니다.

따라서 이 문제는 다음과 같이 풀 수 있습니다.

Nhoj가 배치시킨 소들의 구간별로 나누어서
각 구간에서 소를 한 마리 배치했을 때 먹을 수 있는 최대 합과
두 마리를 배치시켰을 때 얻을 수 있는 추가적인 합을 모두 구한 다음
정렬하여 가장 큰 $N$개를 골라주면 됩니다.

자세히는 Nhoj의 소들을 정렬한 다음, 각 구간에 속하는 거리가 $(p_{i+1}-p_i)/2$ 보다 작은 풀밭들의 합 중 최대값과, 구간의 합을 계산하여 (모든 풀밭들의 맛의 합) - (구간의 최댓값) 들을 수집하면 됩니다.

첫 구간과 마지막 구간은 Nhoj의 소가 한쪽에만 있기 때문에, 소 한마리로 모두 먹을 수 있다는 예외도 생각해야 합니다.

구간의 최대, 최소 차이가 특정한 값보다 작아야 하기 때문에, 투포인터로 어렵지 않게 구현할 수 있습니다.

상세한 코드는 아래에서 확인할 수 있습니다.

정답코드

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll, ll> pll;
typedef pair<int,pair<int,int>> piii;
typedef vector<ll> vl;
typedef vector<pii> vpii;
typedef vector<pll> vpll;
#define pb push_back
#define ff first
#define ss second
#define fast_io ios::sync_with_stdio(false),cin.tie(NULL)

void Solve()
{
    int K, M, N;
    cin>>K>>M>>N;
    vpll patch; 
    vl john, list;
    for(int i=0; i<K; i++) {
        ll p, t;
        cin>>p>>t;
        patch.pb({p, t});
    }
    for(int i=0; i<M; i++) {
        ll f;
        cin>>f;
        john.pb(f);
    }
    
    sort(patch.begin(), patch.end());
    sort(john.begin(), john.end());
    
    int ind=0;
    auto st = patch.begin(), ed = patch.begin();
    ll sum=0, interval_sum = 0, interval_max = 0;

    while(ed->ff<john[0]) {
        sum += ed->ss;
        ed++;
    }
    list.pb(sum);

    while(ind<john.size()-1) {  // john[ind] ~ john[ind+1] 에서의 sum
        sum=0;
        interval_sum = 0;
        interval_max = 0;
        double interval = (john[ind+1]-john[ind])/2;
        ed = lower_bound(patch.begin(), patch.end(), make_pair(john[ind]+1,0ll));
        auto fin = lower_bound(patch.begin(), patch.end(), make_pair(john[ind+1], 0ll));
        st=ed;
        while(st<fin && ed->ff < john[ind+1]) {
            while(ed<fin && ed->ff - st->ff < interval) {
                sum += ed->ss;
                interval_sum += ed->ss;
                ed++;
            }
            interval_max = max(interval_max , sum);
            sum -= st->ss;
            st++;
        }

        list.pb(interval_max);
        list.pb(interval_sum-interval_max);

        ind++;
    }

    sum = 0;
    ed = upper_bound(patch.begin(), patch.end(), make_pair(john[ind],(ll)1e9+1));
    while(ed<patch.end()) {
        sum += ed->ss;
        ed++;
    }
    list.pb(sum);

    sort(list.begin(), list.end(),greater<ll>());

    sum=0;
    for(int i=0; i<N && i<list.size(); i++ ) {
        sum += list[i];
    }
    cout<<sum;
}

int main()
{
    fast_io; 
    Solve();
    return 0;
}

Paired Up (USACO Gold #1)

이 문제는 $N$마리의 소들이 각각 $x_i$ 위치에 $y_i$의 값을 가지고 서있습니다. John은 거리가 $K$ 이하인 소들끼리 쌍을 묶는 문제입니다. 쌍이 매칭되지 않은 소들은 $K$거리 이내에 매칭되지 않은 소가 없어야 합니다. 이 때, 쌍을 맺지 못하는 소들의 값의 합의 최대, 최소를 구하는 문제입니다.

입력으로 들어오는 소들을 정렬했을 때, 이웃한 소들의 거리가 $K$보다 클 수도 있기 때문에, 이웃한 소들끼리 쌍을 맺을 수 있는 체인으로 생각해보려고 합니다. 이웃한 소의 거리가 $K$보다 클 경우, 쌍을 맺을 때 영향을 받지 않기 떄문에 체인별로 나누어 문제를 해결할 수 있습니다.

먼저 각 체인별로 쌍이 맺어지지 않는 소들의 최소를 구하는 문제를 해결해봅니다.

최소를 구하는 방법은 최대를 구하는 것에 비하여 굉장히 간단합니다. 체인의 길이가 짝수인 경우, 이웃한 소들끼리 쌍을 맺어버리면 모든 소가 쌍을 맺을 수 있기 때문에 쌍을 맺지 못하는 소가 0마리가 되어 0이 됩니다.

체인의 길이가 홀수인 경우, 1마리의 소만 없애서 해결할 수 있습니다. 체인을 이루는 소가 없어져도 쌍을 맺을 수 있는 경우는 두 가지입니다.

빠지는 소가 체인에서 홀수번째에 있는 경우
빠지는 소가 이웃한 두 소의 거리가 $K$ 이하인 경우

이 두 경우에는 체인의 길이가 짝수개로 분리되거나 유지되어, 쌍을 맺을 수 있습니다. 이러한 조건을 만족하는 소들 중 값이 최소인 것을 찾으면 간단하게 해결할 수 있습니다.

체인별로 쌍이 맺어지지 않는 소들의 최대를 구해봅시다

한 체인에서 최대한 많은 소를 빼내야 합니다. 직접적인 구현은 어떻게 생각해도 어렵고, 항상 쌍을 맺을 수 있어야 하기 때문에 DP를 떠올릴 수 있습니다. 어느 한 소가 쌍이 맺어지지 않는 소가 되려면, 두 가지의 조건이 필요합니다.

$K$거리 이내에 맺어지지 않은 소가 없을 것
이외의 소들이 쌍을 맺을 수 있을 것

이러한 두 조건을 만족시키도록 따져야 하므로, 한쪽 끝에서부터 DP를 하는 것으로 생각하면 됩니다. $i$ 번째 칸에는 1번부터 $i$번까지 조건에 맞게 빼낼 수 있는 소들의 합의 최대를 저장하였습니다.

저는 맨 앞에서부터 DP를 한다고 가정하고, 풀이를 작성하겠습니다.

DP배열을 채울 때 중요한 점은 첫 번째 조건보다 두 번째 조건입니다. 첫 번째 조건은 이전 값을 이용하여 DP배열을 채울 때 어렵지 않게 고려할 수 있습니다. 하지만 두 번째 조건은 이전 값만으로 해결할 수 있습니다. 그러므로 어떤 소를 쌍을 맺지 않을 때, 그 소보다 앞에있는 소들로 쌍을 맺을 수 있도록 고려해주어야 합니다. (DP를 앞에서부터 채우기 떄문)

특정 소가 사라지더라도 그보다 앞에 있는 소들이 쌍을 맺을 수 있는 경우는 다음과 같습니다.

특정 소가 빠져도 체인이 끊어지지 않을 경우
체인이 끊어져도, 남아있는 소가 짝수마리일 경우

2번조건 때문에 처음부터 $i$ 번째 소까지 짝수마리, 홀수마리를 제외할 때 가능한 최대 합이 달라지게 됩니다. 이를 따로 저장하기 위해서, dp를 2차원 배열로 만들어 처음부터 $i$ 번째까지 제외되는 소가 짝수, 홀수마리인지에 따라 0, 1번칸에 따로 가능한 가지수를 저장하였습니다.

편의를 위하여 소의 번호는 1번부터라고 하고, DP[0][0] 아무것도 제외하지 않는 경우의 수인 0을, DP[0][1]에는 실제로 0마리중 홀수마리를 제외할 수는 없으므로 INT_MIN을 넣어두었습니다.

그러면 이제 $i$ 번째 소를 제외시킬 때 DP를 채울 때, 고려해야하는 경우는 다음과 같습니다.

$i$ 번째 소를 빼지 않을 때
- $i-1$ 번째 값을 그대로 갖고오면 됩니다. 그리고 $i$ 번째 소를 빼내는 경우에 가능한 값과 비교합니다.
체인이 끊어질 때
- 앞에 남는 체인의 길이가 홀수일 경우, $i$ 번째 소와 거리가 처음으로 $K$ 보다 커지는 위치의 1번칸의 값을 이용하여 $i-1$ 번째 값과 비교합니다.
- 반대로 짝수일 경우, $i$ 번째 소와 거리가 처음으로 $K$ 보다 커지는 위치의 0번칸의 값을 이용하여 $i-1$ 번째 값과 비교합니다.
체인이 끊어지지 않을 때
- $i$ 번째 소가 제외가 되면, $i$의 기우성과 동일한 소가 제외되어야, 첫 번째부터 $i$ 번째 소까지 조건에 맞게 $i$ 번째 소와 나머지 소를 제외할 수 있습니다. $i$ 번째 소와 거리가 처음으로 $K$ 보다 커지는 위치에서 $i$의 기우성에 따라 0번칸, 1번칸의 값을 이용하여 $i-1$ 번째 값과 비교합니다.

$K$보다 많이 차이나는 위치를 효율적으로 찾기 위해서, 소들의 위치를 이분탐색이나 투포인터를 이용하여 구현할 수 있습니다.