queuedq's profile image

queuedq

April 17, 2022 00:00

Sum over Subsets (SOS) DP

dynamic-programming

이번 글에서는 다이나믹 프로그래밍으로 Sum over Subsets (SOS) 문제를 푸는 방법을 대해 소개하겠습니다. SOS DP는 Codeforces에서 중상급 난이도의 문제로 종종 출제되는 흥미로운 테크닉이지만, 지금껏 한국어 자료를 찾아보기 어려웠기 때문에 SOS DP를 소개하는 Codeforces 블로그 글의 구성을 참고해서 한국어 소개글을 작성해 보았습니다. 또한 기존 글에서 한발 나아가서 어떤 직관을 통해 SOS DP를 이해할 수 있는지도 소개하려고 합니다.

이 글에서는 다음과 같은 표기를 사용할 것입니다.

  • 비트마스크를 집합처럼 취급합니다. 예를 들어, $1101_{(2)} = 2^0 + 2^2 + 2^3$은 집합 ${0, 2, 3}$과 동일하게 취급할 수 있습니다.
  • 비트마스크 $x$에 대해 $x$의 부분 마스크 $i \subseteq x$는 i & x = i 를 만족하는 비트마스크를 나타냅니다.
  • 비트마스크의 가장 오른쪽의 비트부터 0번째 비트입니다.

Sum over Subsets 문제

다음과 같은 문제를 생각해 봅시다.

수 $2^n$개로 이루어진 배열 $A$가 있다. 비트마스크 $x$에 대해, 함수 $F(x)$를 $x$의 모든 부분 마스크 $i$에 대한 $A[i]$의 합으로 정의하자.

\[F(x) = \sum_{i \subseteq x} A[i]\]

모든 $x=0,\cdots,2^n-1$에 대해, $F(x)$를 구하시오.

느린 풀이: 완전 탐색

가장 간단하게 생각할 수 있는 풀이로는 모든 $x$와 $i$를 돌아보며 i & x = i 를 만족할 때에만 값을 더해주는 방법이 있습니다.

for (int x = 0; x < (1<<n); x++) {
    for (int i = 0; i < (1<<n); i++) {
        if ((i & x) == i) {
            F[x] += A[i];
        }
    }
}

시간 복잡도는 $O(2^n \times 2^n) = O(4^n)$입니다.

덜 느린 풀이: 부분 마스크만 돌아보기

위 풀이는 $i$의 값으로 $2^n$가지 비트마스크를 모두 돌아보는 과정에서 낭비가 발생합니다. $i$가 $x$의 부분 마스크인 경우만 돌아봐도 되기 때문입니다. 실제로 다음 코드를 통해 $x$의 부분 마스크만 돌아보는 것이 가능합니다.

for (int x = 0; x < (1<<n); x++) {
    F[x] = A[0];
    // 0을 제외한 x의 부분 마스크
    for (int i = x; i > 0; i = (i-1) & x) {
        F[x] += A[i];
    }
}

4번 줄의 반복문에서, $i$는 0을 제외한 $x$의 모든 부분 마스크를 역순으로 지나게 됩니다. 그래서 2번 줄에서 0을 따로 처리해 주었습니다.

어떤 원리로 $x$의 부분 마스크만 돌아볼 수 있는지 살펴보겠습니다. $x$의 부분 마스크 $i$와 그 직전 부분 마스크 $i’$을 생각하면, 두 부분 마스크에서 $x$에 포함된 비트만 봤을 때 1 차이가 나는 것처럼 보여야 합니다. 이진수에서 1을 빼면 가장 오른쪽의 1로 설정된 비트가 0으로 바뀌고, 그 오른쪽에 있는 비트들은 전부 1이 됩니다.

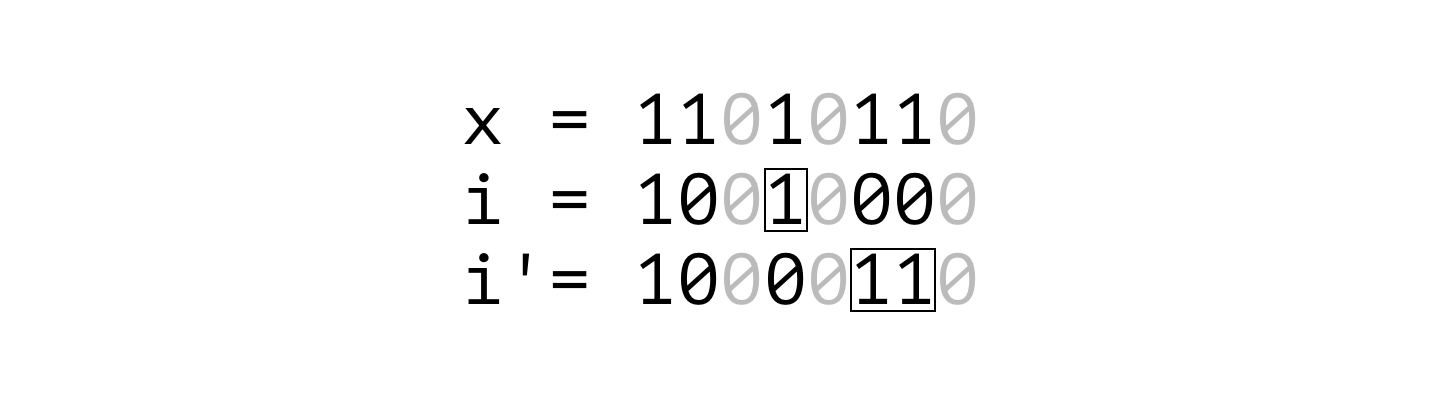
(i-1) & x 를 계산하면 동일한 효과를 얻을 수 있습니다. $i$에서 1을 빼면, 가장 오른쪽의 1로 설정된 비트는 0으로 바뀌고 그 오른쪽에 있는 비트들은 전부 1이 됩니다. $x$와 비트 AND (&)를 취하고 나면, 새롭게 1로 설정된 비트들 중 $x$에 포함되는 비트만 남게 됩니다.

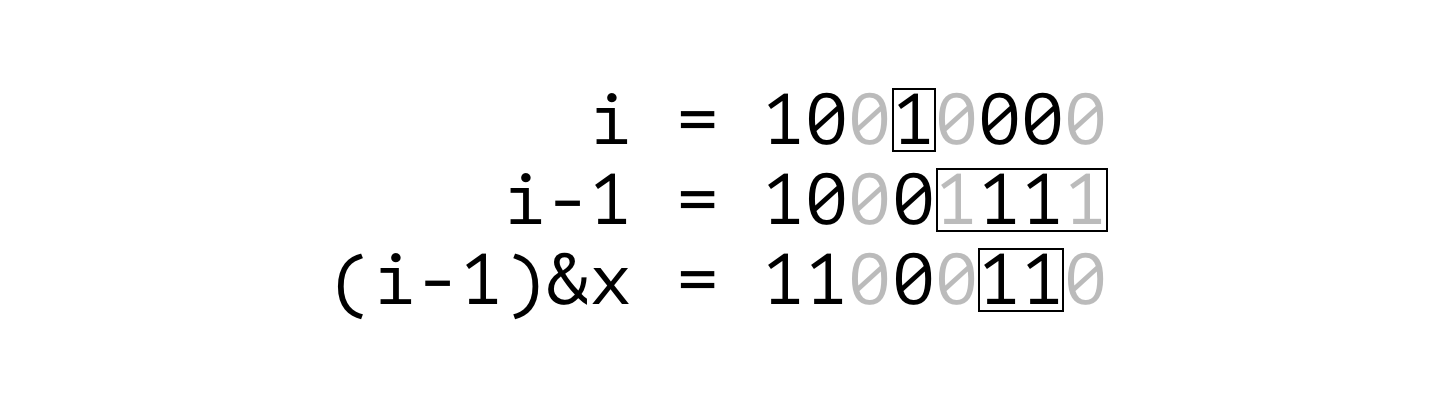
i = x에서 시작해서 위 과정을 반복하면 $x$의 부분 마스크를 역순으로 돌아보는 것이 가능합니다.

이 풀이의 시간 복잡도는 어떻게 될까요? 크기가 $k$인 집합 (1인 비트가 $k$개인 비트마스크)의 부분 마스크의 개수는 $2^k$이고, 크기가 $k$인 집합의 개수는 $\binom{n}{k}$이므로, 이항 정리에 의해 전체 연산 횟수는 $\sum_{k=0}^{n} \binom{n}{k} 2^k = (1+2)^n = 3^n$이 됩니다. 따라서 시간 복잡도는 $O(3^n)$입니다.

빠른 풀이: SOS DP

하지만 위의 풀이에는 여전히 비효율적인 부분이 있습니다. 비트마스크 $i$의 0인 비트가 $k$개라면, $A[i]$는 총 $2^k$번이나 반복해서 더해지기 때문입니다. 자주 함께 사용되는 비트마스크끼리 묶어서 $A[i]$의 합을 계산해 놓고, 이 결과를 재사용한다면 같은 덧셈을 덜 반복할 수 있을 것입니다.

$x$의 부분 마스크 집합을 $S(x)$라고 합시다. 서로 관련 있는 부분 마스크끼리 모이도록 $S(x)$를 분할할 것입니다. 이를 위해서 다음과 같이 $S(x, i)$를 정의하겠습니다. (여기서 $i$는 비트마스크가 아니라, 비트의 인덱스를 나타내는 $[0, n)$ 사이의 정수입니다.)

\[S(x, i) = \{y \subseteq x \mid y \oplus x < 2^{i+1} \}\]

간단히 말하면, $S(x, i)$는 $x$의 부분 마스크 중에서 $i$번째 비트의 왼쪽 비트들이 $x$와 일치하는 것들의 집합입니다. 예를 들어, $S(11010110, 3)$은 다음과 같습니다.

\[S(\pmb{1101}0110, 3) = \{\pmb{1101}0000, \pmb{1101}0010, \pmb{1101}0100, \pmb{1101}0110\}\]

이제 집합 $S(x, i)$를 다음과 같이 더 작은 집합 $S(*, i-1)$들로 분해할 수 있습니다.

  1. $x$의 $i$번째 비트가 0이라면, $x$의 부분 마스크의 $i$번째 비트는 0으로 $x$와 일치하고, 오른쪽 $i-1$개 비트만이 달라질 수 있습니다. 따라서 $S(x, i) = S(x, i-1)$입니다.

  2. $x$의 $i$번째 비트가 1이라면, $x$의 부분 마스크의 $i$번째 비트는 1과 0 모두 가능합니다.

    • $i$번째 비트가 1인 원소들은 오른쪽 $i-1$개 비트만이 $x$와 달라질 수 있으므로, 모으면 $S(x, i-1)$와 같습니다.
    • $i$번째 비트가 0인 원소들은 오른쪽 $i-1$개 비트만이 $x \oplus 2^i$와 달라질 수 있으므로, 모으면 $S(x \oplus 2^i, i-1)$와 같습니다.

정리하면 다음과 같습니다.

\[S(x, i) = \begin{cases} S(x, i-1) & \text{if } i^{\text{th}} \text{ bit} = 0 \\ S(x, i-1) \cup S(x \oplus 2^i, i-1) & \text{if } i^{\text{th}} \text{ bit} = 1 \\ \end{cases}\]

$S(x) = S(x, n-1)$이므로, 아래 그림처럼 $S(x)$를 재귀적으로 분할하는 것이 가능합니다.

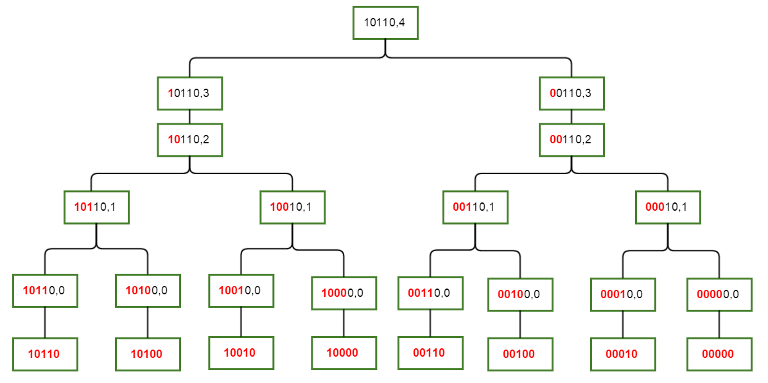
$S(x, i)$의 관계식이 항상 더 작거나 같은 $x$와 $i$ 값들에 의존하고 있으므로, $S(x, i)$들의 관계는 DAG (Directed Acyclic Graph)를 이룹니다. 이 관계를 이용하면 다음과 같은 DP 풀이를 완성할 수 있습니다.

for (int x = 0; x < (1<<n); x++) {
    // 초깃값 설정 (모든 비트가 일치하는 경우)
    D[x][-1] = A[x];
    
    for (int i = 0; i < n; i++) {
        if (x & (1<<i))
            D[x][i] = D[x][i-1] + D[x^(1<<i)][i-1];
        else
            D[x][i] = D[x][i-1];
    }
    
    F[x] = D[x][n-1];
}

덤으로, $D[*][i]$의 점화식이 $D[*][i-1]$에만 의존한다는 사실을 이용하면, 다음과 같이 DP 배열을 재사용해서 메모리 최적화된 코드를 작성할 수 있습니다. 위 코드에 비해 짧으면서, 음수 인덱스도 사용하지 않는다는 장점이 있습니다.

for (int i = 0; i < (1<<n); i++)
    F[i] = A[i];

for (int i = 0; i < n; i++) {
    for (int x = 0; x < (1<<n); x++) {
        if (x & (1<<i))
            F[x] += F[x^(1<<i)];
    }
    // 현재 F[x]에 D[x][i]와 동일한 값이 저장되어 있음
}

SOS DP는 n차원 누적합이다

위의 SOS DP 설명까지가 원글에 담긴 내용입니다. 충분히 짜임새 있는 설명이지만, 저는 처음 SOS DP를 배울 때 집합 $S(x, i)$를 정의하는 방식이 조금 작위적으로 느껴져서인지 $S(x)$의 분할 구조가 잘 와닿지 않았습니다. 그래서 댓글을 둘러보다가, SOS DP는 사실 n차원 누적합이라는 설명을 발견하고 깨달음을 얻었습니다.

이 직관을 설명하기에 앞서 잠시 2차원 누적합을 복습해 봅시다. $n \times m$ 배열 $A$가 주어졌을 때, 누적합 배열 $S$는 다음과 같이 정의됩니다.

\[S[i][j] = \sum_{a \le i} \sum_{b \le j} A[a][b]\]

흔히 2차원 누적합을 다음과 같은 방식으로 계산합니다. 포함배제의 원리를 이용하여 이전 직사각형들의 합집합을 구하는 방식입니다.

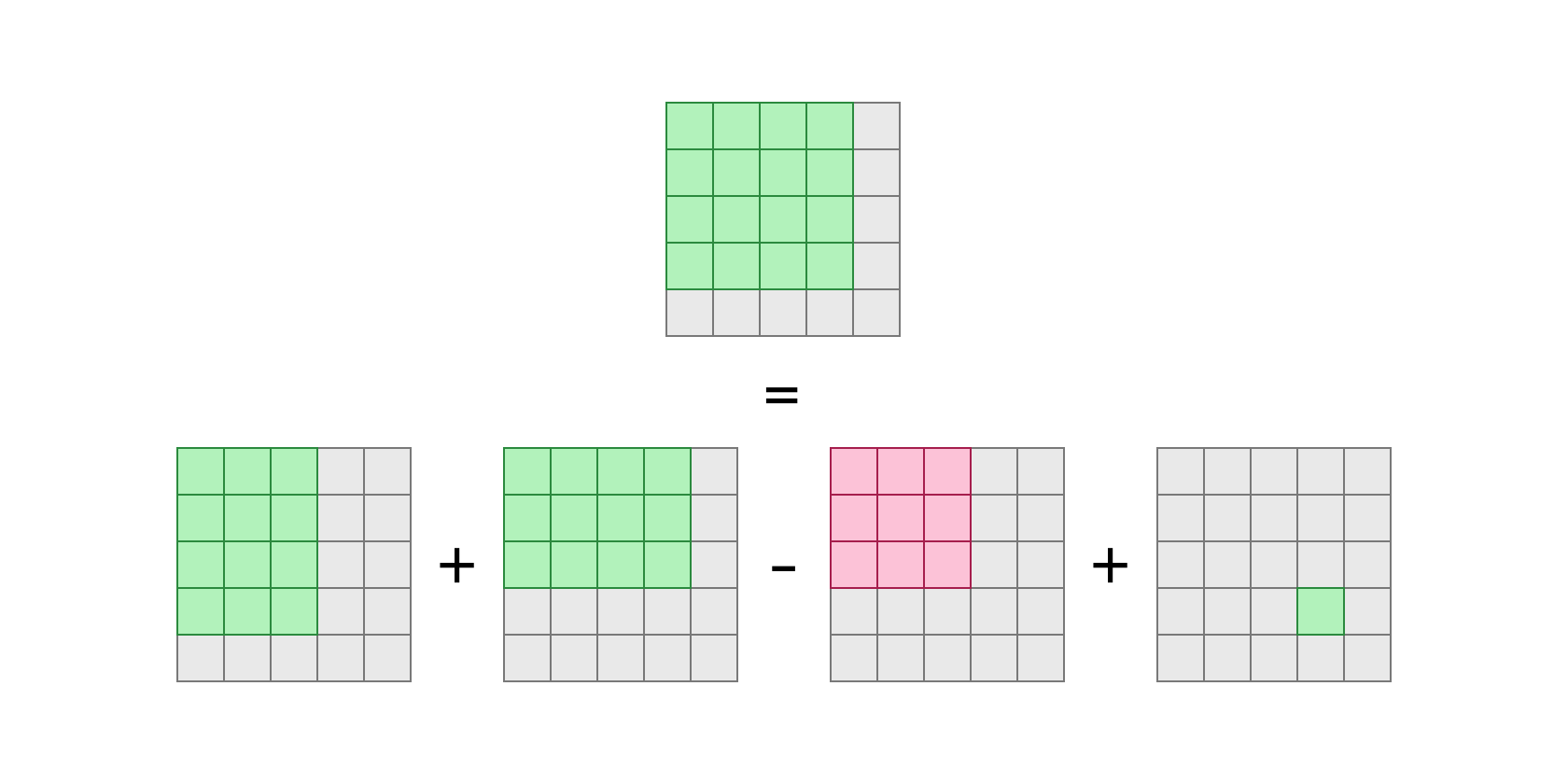
// S[i][-1], S[-1][j]들은 0으로 초기화되어 있음
for (int i = 0; i < n; i++) {
    for (int j = 0; j < m; j++) {
        S[i][j] = S[i][j-1] + S[i][j-1] - S[i-1][j-1] + A[i][j]
    }
}

하지만 위의 방법은 차원이 늘어날수록 더하고 빼야 하는 항의 개수가 지수적으로 증가한다는 단점이 있습니다. 실은 더 단순하고 직관적인 방법이 있습니다. x축과 y축 방향으로 한 번씩 훑으면서 누적합을 구하는 것입니다. 이 방법은 더 높은 차원으로 손쉽게 확장이 가능합니다.

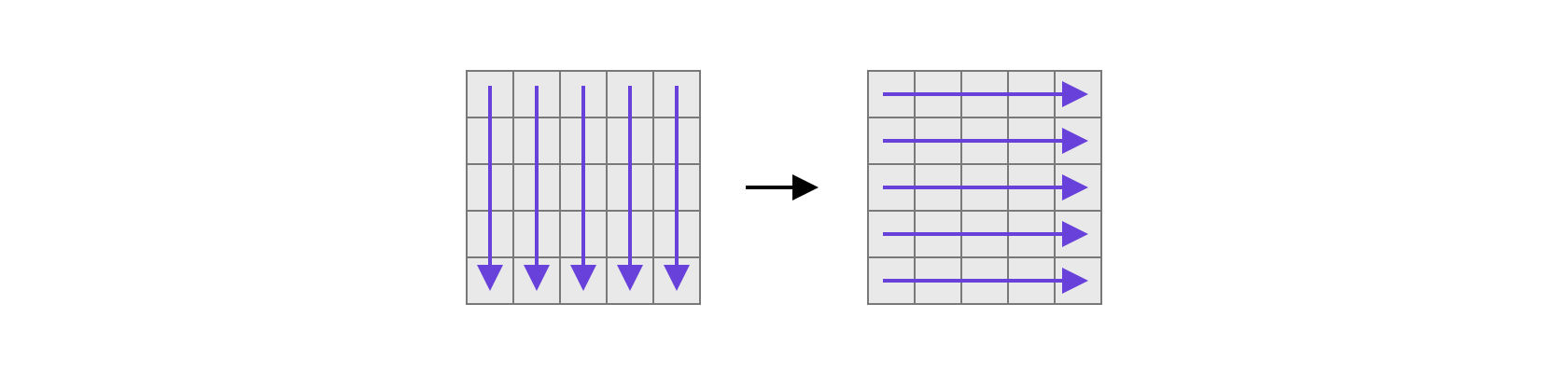
for (int i = 0; i < n; i++)
    for (int j = 0; j < m; j++)
        S[i][j] = A[i][j]
        
// x축 방향으로 훑기
for (int i = 1; i < n; i++)
    for (int j = 0; j < m; j++)
        S[i][j] += S[i-1][j]
        
// y축 방향으로 훑기
for (int i = 0; i < n; j++)
    for (int j = 1; j < m; j++)
        S[i][j] += S[i][j-1]

3차원 누적합을 예로 들어서, 각 축 방향으로 훑은 뒤 $S$에 저장되어 있는 값의 의미를 살펴봅시다.

  1. 처음에 $S[i][j][k]$에는 $a=i,\ b=j,\ c=k$를 만족하는 $A[a][b][c]$가 저장되어 있습니다.
  2. $x$축 방향으로 훑고 나면, $S[i][j][k]$에는 $a \le i,\ b=j,\ c=k$를 만족하는 $A[a][b][c]$들의 합이 저장됩니다.
  3. $y$축 방향으로 훑고 나면, $S[i][j][k]$에는 $a \le i,\ b \le j,\ c=k$를 만족하는 $A[a][b][c]$들의 합이 저장됩니다.
  4. $z$축 방향으로 훑고 나면, $S[i][j][k]$에는 $a \le i,\ b \le j,\ c \le k$를 만족하는 $A[a][b][c]$들의 합이 저장됩니다.

조금 더 나아가서 $n$차원 누적합을 구할 때 $i$번째 축까지 훑은 뒤의 상황을 살펴봅시다. $n$차원 좌표 $x$에 대해서 $S[x]$에 저장되는 값은, $1, \cdots, i$번째 축 좌표가 $x$보다 작거나 같고 $i+1, \cdots, n$번째 축 좌표가 $x$와 일치하는 위치들에 대한 $A$ 값의 합입니다. 왠지 익숙하지 않나요?

다시 Sum over Subsets 문제로 돌아와 봅시다. 각 비트를 하나의 축으로 생각하면, $n$개의 비트로 구성된 비트마스크 $x$는 각 성분이 0 또는 1의 값을 가지는 $n$차원 좌표로 생각할 수 있습니다. $x$의 부분 마스크는 각 성분이 $x$보다 작거나 같은 $n$차원 좌표가 됩니다. 따라서 비트마스크를 $n$차원 좌표로 생각했을 때 $F(x)$는 $n$차원 누적합의 정의와 일치합니다!

여기에 각 축 방향으로 훑는 누적합 알고리즘을 적용하면 위에서 소개한 메모리 최적화 풀이와 일치하는 코드를 얻을 수 있습니다. $0, \cdots, i$번째 축 방향으로 훑은 뒤의 중간 결과 역시 $D[x][i]$와 일치한다는 사실을 알 수 있습니다. 직접 한 번 비교해 보시기 바랍니다.

for (int i = 0; i < (1<<n); i++)
    F[i] = A[i];

for (int i = 0; i < n; i++) {  // 0...n-1 번째 축으로 훑기
    for (int x = 0; x < (1<<n); x++) {
        if (x & (1<<i))  // i번째 축 좌표가 1이므로 누적합 계산
            F[x] += F[x^(1<<i)];
    }
}

연습 문제

참고 자료