알고리즘 문제 접근 과정 11
알고리즘 문제 접근 과정 11
이번 포스트에서도 ‘알고리즘 문제 접근 방법’ 시리즈에서 진행했듯이 특정 문제를 해결하기 위해 가장 낮은 단계의 접근에서부터 최종 해법까지 해결해나가는 과정을 작성합니다.
최대한 다양한 유형의 문제들을 다루어, 많은 문제 유형에서의 접근 방법에 대한 실마리를 드리는 역할을 하려 합니다.
Two Machines - ICPC 2019 Seoul Nationalwide Internet Competition L번
관찰
주어진 문제를 간단히 본다면, 머신 A와 머신 B에서 각각 작업에 걸리는 시간이 다른 N개의 일을, A와 B에 적절히 할당하여 동시에 일을 진행하고, 일처리가 끝나는 시간을 최소화 시키는 문제입니다. 어떤 일은 A에서 굉장히 빨리 처리할 수 있고, 어떤 일은 B에서 빨리 처리할 수 있기 때문에, 일을 잘못 배정하면 걸리는 시간이 천차만별이 될 수 있습니다. 그렇다면, 어떻게 스케줄링해야 시간을 줄일 수 있을까요?
가장 먼저 드는 생각은, 작업들 중에서 가장 적은 시간이 걸리는 일을, 그 때 시간에 해당하는 머신에 할당해주는 것일 겁니다. (250, 1)의 시간이 걸리는 일이 4개가 있다고 한다면, 하나도 A에 할당하지 않고, B에 모두 할당해주는 것이 좋으니, 어떻게 생각하면 어느정도 좋은 답을 구해줄 수 있을 것 같습니다. 하지만 이는 위의 일이 300개 있다고 했을 때, 모든 일이 B에 배정될 것이기 때문에, 300의 시간이 걸리게 되지만, 하나의 일은 A에 할당하게 되면 299의 시간이 걸려 조금 더 줄어들어 답을 구할 수 없음을 알 수 있습니다.
그렇다면, 조금 더 좋은 방법을 생각해볼까요?
우리가 만약에 바로 다음번에 머신에 할당해야하는 일이 무엇인지 모르는 상황이라면, 어떤 방법으로 작업을 머신에 할당해줄 수 있을까요? 이를 해결하기 위해 생각해볼 수 있는 방법으로는 그 일을 A에도 할당해 보고, B에도 할당해 본 다음 가장 적은 시간이 걸리는 할당을 선택해 주는 것입니다. 현재 할당되어있는 머신에 대해서는, 현재 작업을 A에 할당하거나, B에 할당하는 항상 두 가지만 존재하기 때문에, 더 좋은 쪽에 할당해놓아 A와 B가 걸리는 시간이 비슷하게 놓는 것이 가능합니다.
이 방법을 이용하면 위의 두 예시도 실제 답을 구해줄 수 있습니다. 그리고 매 순간 두 기계의 동작시간의 최대가 작도록 할당해놓는다면, 매 순간 A와 B가 걸리는 시간의 차는 아무리 커도 (한 작업에 걸리는 가장 큰 시간)보다 작게 됩니다. 만약 A와 B에 할당된 시간의 차가 작업에 걸리는 가장 큰 시간보다 크다면, 현재와 최대 시간이 같도록 하는 상태에서, 다른 한 쪽에 완전히 포함시킬 수 있기 때문입니다.
위 작업을 B에 할당시켜주는 것이 좋다
이를 굉장히 많이 반복하다보면, A와 B에 걸리는 작업이 거의 절반씩 나눠지는 상태가 될 것이므로, ‘보통 좋은 상태’를 만들 수 있습니다.
하지만 우리에게 이미 작업이 주어졌을 경우에, 이는 ‘어느정도 좋은 것이 보장되는 답’을 구할 수는 있지만, ‘최적의 답’을 구하지는 못할 수 있습니다.
예를 들어, (1, 1)이 2개 있고, (20, 19)이 주어진다면, 위 방법으로는 A와 B에 1을 하나씩 할당한 이후, B에 19를 할당하여 총 20의 시간이 걸리게 됩니다. 하지만 만약 두 일을 모두 A에 할당하고, 세 번째 일만 B에 할당한다면 총 19의 시간이 걸려 더 좋은 답을 얻을 수 있습니다.
이처럼 좋은 방법을 쓰고, 실제 답과의 차이가 얼마 안나는 좋은 방법이 있더라도, 최적의 할당을 해주는 일은 쉽지가 않아, 실제로 할 수 있는 할당들 중 가장 좋은 최적을 찾는 방법을 사용해야 합니다.
그렇다면, 어떻게 실제 할 수 있는 할당들을 해볼 수 있는지 알아보겠습니다.
풀이
가장 쉬운 방법으로는 실제 할 수 있는 모든 할당을 해보는 것입니다. 각 작업은 각각 A, B에 할당하는 두 가지 방법이 있기 때문에 우리는 2^n 가지의 모든 매칭을 해볼 수 있습니다. 이를 실제로 각 일에 대해 걸리는 비용을 합하는 과정까지 구현하여, 그 중 최솟값을 구해줄 수 있고, 총 O(N*2^N)에 문제를 해결할 수 있습니다.
실제로 위 방법은 최적의 답을 언제나 찾을 수 있다는 장점이 있습니다만, 작업의 수가 커질수록 정말 오래걸리는 단점이 있습니다.
즉, 우리는 할 수 있는 모든 것을 해보는 것으로는 답을 구하는데 무리가 있습니다. 이를 해결하기 위해, 우리는 ‘보지 않아도 되는 것들을 제외하고’ 고려할 필요가 있습니다.
이를 구현하기 위해서는 어떤 방법이 필요할까요? 우리가 앞서 이와 비슷한 문제들을 풀어본 적이 있습니다. 이를 해결하기 위해 동적계획법을 이용해봅시다.
만약, 현재 i개의 작업을 보고 있을 때, 머신 A에 j만큼의 시간이 배정되어 있고, B에는 k만큼의 시간이 배정되어있다면, (a, b)의 시간이 걸리는 i+1번 작업을 어떻게 할당해 줄 수 있을까요?
이 때에, i+1번 작업을 A에 할당한다면, i+1개의 작업에 대해 머신 A에 j + a, B에 k만큼의 시간이 걸리게 되고, B에 할당한다면 머신 A에 j, B에 k + b만큼의 시간이 걸리게 될 것입니다.
그렇다면, 우리는 다음과 같은 방법을 생각해볼 수 있을 것입니다.
i개 작업을 쓰면서 A에 j, B에 k의 시간을 배정하는 방법이 존재하는가?
만약 존재한다면, 그 상태에서의 최대 시간은 max(j, k)가 될 것이고, 결국 우리는, n번 작업에 대한 머신 A, B에 할당되어있을 수 있는 모든 경우의 수를 고려하여, 그 중 가장 작은 값이 곧 답이 된다는 것을 알 수 있습니다.
이를 실제 동적계획법으로 구현해보겠습니다.
- F(i, j, k) = (i개 작업을 쓰면서 A에 j, B에 k의 시간을 배정할 수 있는가?)
와 같이 정의하고, 1이면 만들 수 있고, 0이면 만들 수 없다고 놓게 되면, 이는 각 i번 작업을 A에 배정했거나, B에 배정했을 두 가지 경우만 있기 때문에
- F(i, j, k) = max(F(i - 1, j - a, k), F(i - 1, j, k - b))
- F(0, 0, 0) = 1
과 같이 놓을 수 있게 됩니다. 이 때, A에 할당될 수 있는 최대 시간은, M을 (한 작업의 최대 작업시간)이라 놓게 되면, 최대 N*M의 시간까지 될 수 있음을 알 수 있습니다.
우리는 O(1)에 하나의 F를 구해줄 수 있기 때문에, 모든 F에 대해 이를 계산해준다면, 총 채워야하는 F의 수는 O(N * NM * NM) = O(N^3*M^2)이 된다는 것을 알 수 있습니다.
하지만 이는 아직도 작은 범위의 N과 M에 대해서만 답을 구할 수 있어, 아쉬움이 있습니다. 그렇다면 이를 조금 더 빠르게 만들 수 있는 방법이 있을까요?
위에 사용했던 식을 살펴봅시다.
- F(i, j, k)
여기에서 각각 j와 k에 A와 B에 할당되어있는 시간을 인자로 쓰고 있고, 실제 F에는 가능한지 여부 1과 0만 사용되고 있습니다. 하지만 만약에 F가 우리에게 필요한 값을 가지고 있다면, 더 적은 인자만 쓰고도 문제를 해결할 수 있지 않을까요?
여기에서, 우리는 원래 문제에서 한가지 생각해 볼 것이 있습니다. 만약 A에 j만큼의 시간이 할당되어 있었고, B에 k만큼의 시간이 할당되어 있다고 합시다. 그렇다면, A에 j + 1만큼의 시간을 할당할 수 있다면, B에는 k보다 큰 시간이 할당될 수 있을까요? 절대 그런 경우는 없을 것입니다. 우리는 아무리 안좋은 상황이어도, 항상 A에 j, B에 k의 시간이 할당된 상태에서, B의 작업을 0개 이상 A로 옮기기만 해도 항상 B에 k만큼의 시간을 보장해줄 수 있습니다. 즉, A에 배정된 시간이 커질수록 항상 B에는 더 작거나 같은 시간을 배정해줄 수 있기 때문에, A가 증가하면 B는 감소하는 형태로 작업이 할당이 됩니다.
이를 실제로 반영하여 F를 생각해줍시다.
- F(i, j) = (i번 작업까지 머신 A에 j만큼의 시간을 배정해줄 때, B에 배정할 최소 시간)
이와 같이 정의하게 되면, F는 다음과 같이 표현이 가능해집니다.
- F(i, j) = min{F(i - 1, j) + b, F(i - 1, j - a)}
- F(0, 0) = 0
즉, 앞서서 정의한 F를 지금까지 잘 구해놓은 상황이라면, 1~i-1번 작업까지 처리한 이후, 새로운 i번째 작업을 배정하는 경우는 이를 A 혹은 B에 배정하는 각각의 경우가 존재하게 됩니다.
이 상황에서 A가 i번 작업까지 끝났을 때에 j 시간을 사용했다면 이는 i번을 A에 배정하고, 그 이전에 j-a의 시간까지 작업을 했던 상황, 혹은 B에 배정하고 A는 이전에 j 시간 작업을 한 상황임을 의미합니다. 이 시점에, 새로운 작업을 A 혹은 B 이외에 다른 곳에 배정하는 경우는 존재할 수 없기 때문에, 우리는 모든 경우를 잘 처리했음을 알 수 있습니다.
그렇다면 위 식을 채우는데에는 얼마의 시간이 걸리게 될까요?
모든 작업을 보기 위해서는 총 N개의 작업에 대해 F를 채워야합니다. 이 때, A가 가질 수 있는 최대 작업 배정은, 모든 작업이 다 A에 배정되는 경우입니다. 이 때 A가 가지는 총 시간은 $N * M$이 되기 때문에, 전체 F의 상태 수는 $N^2 * M$이 됩니다.
F의 식은 모두 $O(1)$만에 처리가 가능하기 때문에, 총 시간 복잡도는 $O(N^2 * M)$이 되고, 문제 상황에서 N과 M 모두 250이하이기 때문에, 1초 안에 해결할 수 있음을 알 수 있습니다.
Byte Coin - ICPC Seoul Nationalwide Internet Competition 2019 C번
관찰
우리가 하루에 코인을 사는 것과 동시에 파는 것을 하는 일이 있을 수 있을까요? 만약 a개의 코인을 사고, b개의 코인을 판다고 한다면, a-b개의 코인을 사거나 혹은 b-a개의 코인을 파는 것만으로 똑같은 결과를 낼 수 있습니다. 즉, 우리는 하루에 항상 코인을 사거나 혹은 팔거나, 아무것도 하지 않는 3가지의 경우만 있을 수 있습니다.
우리는 매일마다 코인을 사고 팔고, 아무것도 안하는 세 경우가 있으므로, 이를 매일마다 결정해준다면 총 3^n만큼의 경우의 수가 있을 수 있습니다. 그렇다면, 하루에 사기로 결정했다면 얼마나 많은 코인을 사고, 판다면 얼마나 많은 코인을 팔아야할까요?
먼저, i번 날에 a개를 팔고, i + 1번 날에 b개를 파는 경우를 생각해봅시다. 이 때, i + 1번 날의 코인의 값이 더 크다면, i번 날의 a개 또한 i + 1번 날에 파는 경우가 항상 더 많은 이득을 번다는 것을 알 수 있습니다. 반대도 마찬가지로 b개를 i번 날에 한 번에 팔면 더 많은 이득을 벌 수 있습니다. 이를 일반화하면, 연속된 날들에 대해 코인을 팔거나 아무것도 안하기로 결정했다면, 이 중 가장 가격이 큰 날에 몰아서 파는 것이 항상 좋은 결과를 내게 됩니다.
반대도 마찬가지로, 연속된 날들에 코인을 사기로만 결정했다면, 이 중 가격이 가장 작은 날에 몰아서 사는 것이 가장 좋은 결과를 내게 됩니다.
- 2, 3, 4, 5일에 k개의 코인을 팔기로 결정했다면, 가장 가격이 큰 날인 2일째에 팔면 총 7 * k만큼의 비용을 벌게 됩니다.
- 2, 3, 4, 5일에 k개의 코인을 사기로 결정했다면, 가장 가격이 작은 5일째에 산다면 총 2 * k만큼의 비용만을 사용하여 코인을 구매할 수 있습니다.
이제 우리는 시간 구간들을, 연속된 파는 경우, 연속된 아무것도 안하는 경우, 연속된 사는 경우들로 나눌 수 있게 되었습니다. 하지만 사실 아무것도 안하는 경우는 양쪽에 존재하는 파는 경우, 혹은 사는 경우에 항상 포함시키는 것이 더 좋은 결과를 냅니다.
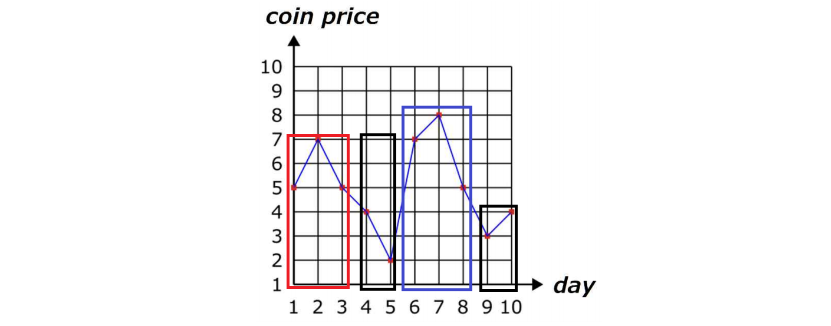
파는 구간을 파란색, 사는 구간을 붉은색, 아무것도 하지 않는 구간을 검은색으로 표시하게 되면, 첫 검정 구간은 항상 왼쪽에 있는 붉은 구간에 합치는 것이 더 좋은 결과를 내게 됩니다. 위 상황에는 검정 구간에 있는 값들이 붉은 구간의 최솟값보다 작기 때문에 더 싼 값에 코인을 살 수 있고, 막약 더 크다 하더라도 붉은 구간의 최솟값에 영향을 주지 않으므로 결과는 항상 더 좋은 방향으로 만들어집니다. 이는 파는 경우에도 똑같이 적용되어, 파란 구간의 최댓값 이상일 경우 더 많은 돈은 얻을 수 있습니다. 결국 우리는 모든 구간을 연속된 사거나 혹은 파는 구간으로 만들 수 있게 됩니다.
풀이
우리는 사고 파는 일자들을 연속된 구간들로 나누어 사고 파는 것을 번갈아 해야한다는 것을 알게 되었습니다. 하지만 우리는 아직도 각 구간에서 얼마나 많이 사고, 얼마나 많이 팔아야하는지는 알아보지 않았습니다.
처음에 우리는 아무 코인도 가지고 있지 않기 때문에, 첫 구간에는 항상 코인을 사는 붉은색 구간을 가지게 됩니다. 일단 얼마를 사는지 생각하지 않고, 이 구간에 사는 코인의 최소 가격 a만을 두고 생각해보도록 합시다. 그리고 이 다음 파는 코인의 최대 가격을 b라고 합시다. 만약, a가 b보다 크다고 한다면, 우리는 절대로 돈을 벌 수 없습니다. 이 경우에는 오히려 a에서 사서 b에서 파는 것보다, b에서 사는 것이 코인을 더 싸게 살 수 있게 됩니다. 즉, 우리는 다음 구간의 가격이 감소할 때, 이를 붉은 구간과 합쳐줘야 한다는 사실을 알 수 있습니다. 이와 마찬가지로 파란 구간에 대해서는, c에서 팔고 d에서 사는게 손해일 경우, c에서 팔지 않고 d에서 파는게 더 효율적이므로 파란 구간에 합쳐주는게 더 많은 이익을 볼 수 있습니다.
즉, 우리는 빨간 구간과 파란 구간이 반복될 때, 항상 빨간 구간 뒤에는 가격이 더 올라가고, 파란 구간 뒤에는 가격이 더 내려가야 한다는 것을 알 수 있습니다.
이를 만족하는 구간에서는
항상 살 때가 팔 때보다 더 가격이 싸고 판 이후에는 코인의 가격이 감소함
위 두 성질을 만족하게 되는데, 이 때문에 우리는 최대한 많이 사서 모두 파는 것이 가장 많은 이득을 볼 수 있게 됩니다. 이를 더 자세히 살펴보겠습니다.
다음과 같은 붉은색-파란색 구간들로 나누어져 있을 때, 1번에서 사서 4번에서 팔면 더 많은 이득을 볼 수 있지 않을까라는 생각이 들 수 있습니다.
하지만 우리에게는 중요한 조건이 있습니다. 바로, ‘판 이후에는 코인의 가격이 감소함’이 이에 중요한 역할을 합니다. 우리가 첫 구간에서 3개의 코인을 샀다고 합시다. 만약 하나의 코인을 4번 구간까지 기다린 이후에 판다고 했을 때, 우리는 [4번] - [1번]의 가격을 벌어들일 수 있습니다. 하지만, 이 중간 과정에 [2번] - [3번] = 1을 더하게 된다면, 우리는 [4번] - [1번] + [2번] - [3번] = [4번] - [1번] + 1로 1원을 더 벌 수가 있게 됩니다. 즉, ‘판 이후에는 코인의 가격이 감소함’을 통해, 항상 이 사이에 있는 [파란 구간 - 빨간 구간]은 양수를 만족하게 되므로, 이 중간에 있는 사고 파는 과정을 하는 것이 항상 더 많은 돈을 벌 수 있게 해줍니다.
따라서 우리는 매 번, 가능한 많은 코인을 산 이후에 바로 다음번에 파는 것이 결과적으로 항상 이득을 내게 되기 때문에, 매 순간 사고 팔 수 있을 때마다 모두 사고 한 번에 되파는 것이 가장 큰 이익을 낼 수가 있게 됩니다.
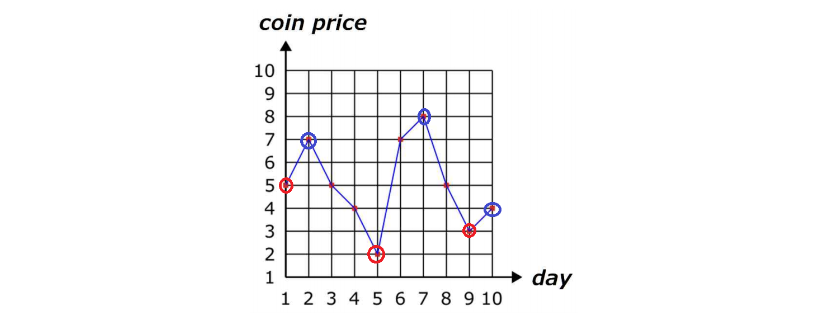
주어진 그래프에서 붉은 구간과 파란 구간을 찾는 방법은, 항상 붉은 구간은 최솟값을 찾아야하므로, 내림차순을 만족하는 가장 끝 값들을, 파란 구간은 최댓값을 찾아야하므로 오름차순을 만족하는 가장 끝 값들을 정하게 되면, 매 구간의 최솟값과 최댓값을 구해줄 수가 있습니다. 내림차순의 끝 이후에는 오름차순이, 오름차순의 끝 이후에는 내림차순이 이어지므로 항상 새로운 파란 구간, 빨간 구간으로 이어지게 되어, 이와 같은 선택이 항상 최선이 됩니다.
이는 이전 원소와의 크기 비교를 이용해서 매 순간 O(1)에 붉은 구간인지 파란 구간인지 판단해줄 수 있고, 모든 원소들을 한 번씩만 보게 되어, O(N)에 문제를 해결할 수 있습니다.
다만, 마지막 날이 내림차순의 끝이 될 경우 코인들을 사고 날짜가 끝나게 되는데, 산 코인들을 다시 모두 되팔아서 마지막 날에 아무것도 하지 않은 것과 같은 역할을 수행해줘야 합니다.
보석 도둑 - COCI 2010/2011 COCI 2013/2014 Contest #1 4번 LOPOV
관찰
우리가 문제에서 주어진 조건을 통해서 살펴볼 수 있는 것이 있을까요?
- 가방에는 아무리 많아도 최대 1개의 보석만을 넣을 수 있습니다.
- 가방에는 최대 무게가 Ci인 보석만을 넣을 수 있습니다.
위에 주어진 조건을 본다면, 가방 하나에는 아무리 많아도 1개의 보석만을 넣을 수 있으므로, 보석 하나를 가방에 넣게 된다면, 남아있는 보석과 가방은 이전에서 1개씩 사라진 것들 중 고려하면 된다는 것을 알 수 있습니다.
즉, 우리는 가방과와 보석들을 각각 한 개씩 매치하여 상덕이가 가지는 가격이 최대가 되도록 매치하는 문제로 표상할 수 있습니다.
그렇다면 주어진 보석들을 가방과와 어떻게 매치해주면 좋을까요?
앞선 예시에서 나왔던 보석들과 가방들을 살펴보겠습니다.
우리는 위의 5개의 보석이 있을 때, 각 가방들을 보석에 매치시키는 방법으로 문제를 해결할 수 있습니다. 그렇다면, 어떤 방법으로 매치를 진행할 수 있을까요?
우리는 가장 먼저, 가장 가격이가 큰 보석을 매치시켜주는 방법을 생각해볼 수 있습니다. 어차피 가격을를 최대화시키는 문제이므로, 가장 가격이가 큰 보석을 넣을 수 있다면 어느정도 합리적으로 보입니다. 이 방법대로 문제를 해결해보겠습니다.
먼저, 무게가 5인 가방을 보면, 모든 보석을 담을 수 있습니다. 그러므로 가장 가격이가 큰 5번을 가방에 매치 시켜주겠습니다.
다음으로는 무게가 3인 가방을 보겠습니다. 이 때엔 가격이가 8인 1번 보석이 가장 좋아 보입니다. 2번 가방을 1번 보석에 매치 시켜주겠습니다.
이제 무게가 1인 가방을 보겠습니다. 하지만 이 때에는 남은 보석들 모두 가방에 넣을 수 없으므로, 우리는 더 이상 보석을 담을 수 없습니다.
하지만, 만약 우리가 1번 보석을 무게가 1인 가방에 담았다면, 우리는 무게가 3인 가방에 2번 보석을 담아 25의 가격을 만들 수 있었습니다.
분명 가격이가 가장 큰 보석을 담는 것은 어느정도 합리적으로 보였었습니다. 그렇다면 왜 이런 결과가 나온 것일까요? 가격이 가장 큰 보석을 담는다는 접근이 잘못된 것일까요?
그 이유는 우리가 가방을 매치시킨 순서에 있습니다. 우리는 지금 가방의 무게에 상관없이 무작위 순서대로 매치를 시켰습니다. 이를 통해 우리는 ‘더 작은 가방에도 담을 수 있는 보석을 큰 가방에 담는다’라는 문제가 생겼습니다. 1번 보석은 무게가 1인 가방에도 담을 수 있었지만, 3인 가방에 담아, 1인 가방이 다른 보석을 담지 못했기 때문입니다.
풀이
그렇다면 이 문제를 어떻게 해결할 수 있을까요?
우리는 가방을 무게 순으로 정렬한 뒤, 무게가 작은 가방부터 매치를 진행하는 것으로 해결할 수 있습니다.
앞선 예시를 다시 한 번 살펴보겠습니다.
우리는 가방을 무게 순으로 정렬하여, 1, 3, 5인 가방을 보석에 매치시켜야 합니다.
먼저 무게 1 가방을 매치시킬 후보를 찾으면, (1, 8)만이 가능합니다. 그러므로 1번 보석을 1인 가방과와 매치해주겠습니다.
다음으로 무게 3인 가방을 보겠습니다. 후보는 (2, 7), (3, 6)이 있습니다. 이 때, 가격이가 가장 큰 것은 (2, 7)이므로 2번 보석에 매치시켜 주겠습니다.
이제 무게 5인 가방을 보겠습니다. 이 때, 새로이 후보에 추가될 수 있는 보석으로는 (4, 9)와 (5, 10)이 있습니다. 이 때, 무게 3인 가방 후보였던 (3, 6)도 무게 5인 가방의 후보가 될 수 있을까요?
답을 ‘물론 될 수 있다’입니다. 우리는 가방들을 무게 순으로 보고 있기 때문에 항상 다음에 확인하게 되는 가방은 이전의 가방보다 더 무게가 커지게 됩니다. 즉, 우리는 현재 보고 있는 가방이가 이전 가방의 후보들 또한 항상 포함시킬 수 있음을 알 수 있습니다.
앞선 (1, 8)을 무게 3인 가방에 담아서, (2, 7), (3, 6)을 무게 1인 가방에 담을 수 없었던 경우같은 일은 발생할 수 없다는 것이죠.
결국, 우리는 무게가 작은 가방부터 순서대로, ‘자신이 담을 수 있는 보석 중 가장 가격이가 큰 보석을 담기’를 적용시킨다면, 어떠한 경우에도 항상 남아있는 후보군 들 중에서 가장 가격이가 큰 보석들을 담을 수 있습니다.
어차피 다음으로 오는 가방들에서 이전에 있던 후보군들을 모두 포함시킬 수 있는데, 굳이 현재 남아있는 가장 가격이가 큰 보석을 담지 않을 이유가 없음은 쉽게 알 수 있고, 이로써 현 방법이 최선임을 알 수 있습니다. (만약 모든 가방들에 대해, 가격이가 최선이 아닌 (a1, b1)인 보석이 있고 이 보석을 c라는 가방에 담아야 최선이 된다면, c인 가방에서 (a1, b1)인 보석이 아닌 가격이가 더 크거나 같은 보석을 사용한다면 항상 가격의 합이 더 크거나 같아지므로, 항상 최선을 선택하는 것이 답이 됨을 알 수 있습니다)
이로써, 가방들을 순서대로 정렬하는데 O(KlgK), K개의 가방을 각각 N개의 보석에 매치시켜 주는데 O(NK)가 필요하므로, 시간복잡도는 $O(NK+KlgK)$가 걸리게 됩니다.
개미 - Waterloo’s local Programming Contests 2004 September 19 B번 Ants
관찰
어떤 개미는 다른 개미를 마주치는 것을 반복하여 계속해서 왼쪽, 오른쪽으로 방향을 바꾸게 될 수 있습니다. 개미가 항상 처음 방향대로만 이동하지 않을 수 있으므로, 우리가 어떤 개미가 막대 위를 언제 벗어나는지 알고 싶다면, 그 개미가 이동하게 되는 경로를 실제로 구하는 것으로 문제를 해결할 수 있습니다.
하지만 한 개미가 이동하게 되는 경로는 다른 개미들의 이동에 따라 바뀌고, 어디에서 마주치냐에 따라서도 달라지므로 각 개미들이 막대를 빠져나오는 시간을 하나하나 계산하기에는 어려움이 있을 수 있습니다. 그러나 만약 우리가 개미들이 이동하는 것을 시간에 따라 시뮬레이션 해줄 수 있다면, 어떤 시간에 어떤 개미가 어디에 있는지, 어디에서 마주치는지 알 수 있으므로 이를 쉽게 해줄 수 있습니다.
그러나 예시에서 봤듯, 개미들은 꼭 정수의 시간만큼씩 흐르지 않을 수 있어 정수 시간을 이용해 시뮬레이션 하는 것은 어려움이 있습니다. 그렇다면, 어떻게 시뮬레이션을 잘 할 수 있을까요?
이를 알기 위해서는 각 개미들이 언제 마주치는지 알아야 합니다. 처음 모든 개미들은 정수 위치에 있으므로 어떠한 두 개미도 늘 1, 2, 3 과같이 정수 거리 떨어져있게 됩니다. 이 때, 2 이상의 거리는 항상 1초 후에도 정수위치에 존재하고, 바로 마주치거나 아직 마주치지 못했을 것이므로, 거리 1의 경우를 생각합시다.
1만큼 떨어진 두 개미는 0.5초 후에 0.5만큼 거리에서 마주치게 됩니다.
이 때, 다른 개미들은 이 두 개미와 1 이상 떨어져있으므로, 다른 개미들은 두 개미가 마주친 위치에서 적어도 1이상 떨어져있게 됩니다. 즉, 우리는 두 개미가 마주친 이후 0.5초가 지나더라도 거리는 1만큼 밖에 차이가 나지 않으므로, 이 두 개미와 다른 개미들이 그 순간 마주치게 되거나, 만나지 않는 경우만 존재한다는 것을 알 수 있습니다. 즉, 우리는 개미들이 마주치는 순간은 항상 0.5초 단위로 나눌 수 있게 되어, 우리는 0.5초씩 진행하여 시뮬레이션 하는 것으로 모든 개미들이 막대를 나가는 순간을 계산해줄 수 있습니다.
1.5의 개미와 2.5의 개미는 1만큼 떨어져있으므로, 0.5초 후에 마주침
이는 결국 모든 개미들의 0.5초후의 위치를 계산해주는 것을 반복하는 것이므로, (막대에서 빠져나가는 시간) * N 만큼의 시간이 걸리는 것으로, 문제를 해결할 수 있습니다.
풀이
사실 우리는 실제로 시뮬레이션 하지 않고, 약간의 관찰만을 해주게 되면, 문제를 쉽게 해결할 수 있습니다. 앞선 관찰에서 각 개미들의 위치를 알기 어려웠던 이유는 한 개미가 보고있는 방향을 바꾸는 일이 굉장히 많이 일어날 수 있어, 각 개미들이 어떤 경로를 통해 이동하는지 알기 쉽지 않았다는 점입니다. 하지만 우리에게 중요한 것은 각 개미가 어떤 경로로 언제 막대에서 떨어지는지가 아닌, 모든 개미가 막대에서 떨어지는 시간이라는 것을 이용하면, 문제를 좀 더 쉽게 생각할 수 있습니다.
아까의 그림 예시를 봅시다.
두 개미가 마주쳐서 1번 개미는 오른쪽을 보고 있다가, 1.5의 위치에서 마주쳐 왼쪽을 보고 이동하게 됩니다. 하지만 이것을 개미의 번호가 없다고 생각하고 본다면 어떻게 될까요? 1번과 2번 개미는 서로 마주쳐 반대로 걸어갔지만, 만약 반대로 걸어가지 않고 그대로 걸어갔다면 어떻게 될까요?
그 결과는 위 그림과 하나도 빠짐없이 같아질 것입니다. 두 개미는 원래 걸어가던 대로 걸어가면서, 매겨져있던 번호만 바뀔 뿐, 마주친 이후에 왼쪽으로 이동하는 개미와 오른쪽으로 이동하는 개미가 한 마리씩이라는 점은 달라지지 않으므로, 그냥 지나쳐 간다 생각해도 문제가 없게 됩니다.
이를 이용하여, 모든 개미들에 대해, 다른 개미들이 없이 보고있는 방향으로 걷는다고 생각해도 모든 개미들이 막대에서 나가는 것에는 영향을 주지 않게 되어, 각 개미가 혼자 걸을 때 벗어나는 시간들 중 가장 큰 값이 되는 순간, 모든 개미들이 막대에서 벗어난다는 것을 알 수 있습니다.
결국 막대의 길이와 상관없이, 각 개미들과 막대의 거리만 중요하게 되므로, 총 O(N)에 문제를 해결할 수 있습니다.
코드
Two Machines
#include <bits/stdc++.h>
#define INF 1e9
using namespace std;
int n, res = 1e9;
int dp[300][70000];
int main(){
int i, j, k, a, s;
scanf("%d", &n);
for(i = 1; i <= n; i++){
scanf("%d %d", &a, &s);
for(j = 0; j <= 250 * i; j++){
dp[i][j] = dp[i-1][j] + s;
if(j - a >= 0) dp[i][j] = min(dp[i][j], dp[i-1][j-a]);
}
}
for(i = 0; i <= 250 * n; i++) res = min(res, max(dp[n][i], i));
printf("%d", res);
return 0;
}
Byte Coin
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int n;
ll w, a, c = 1e9;
int main(){
int i;
scanf("%d %lld", &n, &w);
for(i = 0; i < n; i++){
scanf("%lld", &a);
if(a > c) w = (w / c) * a + w % c;
c = a;
}
printf("%lld", w);
}
보석 도둑
#include <bits/stdc++.h>
#define ll long long
using namespace std;
struct data{int m,v;};
ll sum;
int n,k;
int carr[300010];
data arr[300010];
bool compare(data d1,data d2){
return d1.m<d2.m;
}
priority_queue <int,vector<int>,less<int>> pq;
int main(void){
int j=0;
scanf("%d %d",&n,&k);
for(int i=0;i<n;i++)scanf("%d %d",&arr[i].m,&arr[i].v);
for(int i=0;i<k;i++)scanf("%d",&carr[i]);
sort(arr,arr+n,compare);
sort(carr,carr+k);
for(int i=0;i<k;i++){
while(j<n&&arr[j].m<=carr[i]){
pq.push(arr[j++].v);
}
if(!pq.empty())sum+=pq.top(),pq.pop();
}
printf("%lld",sum);
return 0;
}
개미
#include <bits/stdc++.h>
using namespace std;
int T, l, n;
int main(){
int i, min1, max1, a;
scanf("%d", &T);
while(T){
scanf("%d %d", &l, &n); min1 = 0; max1 = 0;
for(i = 0; i < n; i++){
scanf("%d", &a);
min1 = max(min1, min(a, l - a));
max1 = max(max1, max(a, l - a));
}
printf("%d %d\n", min1, max1);
T--;
}
return 0;
}