Differential Privacy
들어가며
IT기술들이 발전하며 개개인의 데이터 가치는 나날이 높아지고, 그만큼 관심이 많아지고 있습니다. 얼마 전에는 구글과 메타가 개인정보 불법수집으로 인해 과징금을 내는 등, 회사들에서도 개인정보에 관심을 가지고 있습니다.
개인정보들 중에서도 조금더 민감한 정보들이 있을 수 있습니다. 이름이나 생일같은 정보는 하나만 있으면 개인을 특정하기 굉장히 어렵지만, 희귀병이 있다거나 하는 등 한 가지의 정보만 있더라고 개인을 특정할 수 있는 문제들도 있습니다.
이번에는 이러한 데이터들을 어떻게 privacy를 지키면서 관리할 수 있는지에 대해 알아보려고 합니다.
Differential privacy
이전부터는 Database에 데이터를 관리하면서, privacy를 어떻게 보장할 수 있는지에 대해 연구하였습니다. Database에서 몇 개의 쿼리를 통해서 어느 한 사람의 정보를 얻을 수 있다면, 그 사람의 privacy는 보장되지 못하는 것입니다.
예를 들어, Database에서 희귀병에 걸린 사람의 수를 count하는데, 어느 Alice라는 사람이 Bob으로 바뀌었을 떄 숫자가 증가한다면, Bob이라는 사람이 희귀병이라는 사실을 알 수 있습니다.
위와 같이 Database에서 모르는 정보를 얻을 수 있는 경우는 privacy하지 않기 때문에, 이러한 것을 불가능하도록 noise를 추가하여 데이터 하나 하나가 쿼리 결과물에 큰 영향을 미치지 않도록 하는 것이 Differential privacy입니다.
이를 수식으로 표현한다면, 다음과 같습니다.
데이터셋 $D_1$이 있습니다. 그리고 $D_1$과 하나의 데이터를 제외한 나머지 데이터가 전부 같은 데이터셋 $D_2$가 있습니다.
그리고 데이터셋을 입력으로 가지는 알고리즘 $A$라고 가정합니다.
해당 조건하에서, 다음 식을 만족하는 만족하는 경우, $D_1$을 $\epsilon$-differential privacy라고 합니다.
$ Pr[A(D_1) \in S] \leq e^\epsilon \times Pr[A(D_2) \in S]$
이 식에서, $\delta$항을 추가한다면 $(\epsilon, \delta)$-differential privacy 라고 합니다.
$ Pr[A(D_1) \in S] \leq e^\epsilon \times Pr[A(D_2) \in S] + \delta$
위 식들에서, $\epsilon$이 작다는 것은 결국 두 Dataset에서 임의의 결과물이 나올 확률이 비슷하다는 것을 의미하게 됩니다. 즉, 식에서 $\epsilon, \delta$가 작을수록 privacy가 지켜지는 database가 됨을 판단할 수 있습니다.
Sensitivity
위에서는 privacy의 기준을 제시하였습니다. 그러면 저 기준을 통해서 Dataset의 privacy를 더욱 강화할 때, 어느정도의 noise를 더해야 원하는 만큼 $\epsilon$이 변화하게 되는걸까요?
이것을 측정하기 위해서는 데이터셋의 Sensitivity가 필요합니다. Sensitivity는 데이터셋 $D_1$과 하나의 원소만 다른 $D_2$, 그리고 함수 $f$가 있을 때, 다음과 같이 정의합니다.
$\Delta f = max|f(D_1) - f(D_2)|_1 $
어떤 함수 $f$에 대해서 이 Dataset의 원소 하나가 만들어낼 수 있는 가장 큰 차이를 계산하는 값입니다. 원소 하나가 많은 차이를 만들어 낸다는 것은 그만큼 특이한 데이터라는 의미이고, 그 데이터는 공격자에 의해 알려질 가능성이 높다고 볼 수 있습니다.
Noise
위에서 본 Differential privacy와 어떤 dataset과 함수의 Sensitivity를 통하여 이를 안전하게 만들 수 있는 노이즈를 추가할 수 있습니다.
만약에 Gaussian noise를 더한다고 가정해봅시다. Dataset $D$, 함수 $f$에 대해서, 원하는 $(\epsilon,\delta)$-differential privacy가 되기 위해서는, 다음과 같은 노이즈를 더해야 합니다.
$N(0, (\Delta f)^2 \cdot \sigma ^2 )$
그 외에도 Laplace noise 등 여러가지 방법을 통해서 분포를 해치지 않으며 노이즈를 추가할 수 있습니다. 노이즈는 적게 더할수록 데이터의 손상이 적어지고, 많이 더할수록 데이터의 손상이 커질 수 밖에 없습니다. 그렇기 때문에,
Deep learning with differential privacy
등장개요
인공지능이 발달함에 따라서, 이곳 저곳에서 인공지능을 사용하기 위해 데이터를 모으고, 인공지능을 적용시키고 있습니다. 하지만 인공지능의 기술 발전에 비해서 보안은 큰 관심을 받지 못하고 있습니다.
생체 데이터와 같이 개인에게 민감한 정보도 많이 다루고 있는 인공지능에 대해서, 모델을 통해 학습 데이터를 복원하는 Inversion attack은 치명적인 취약점입니다. 이러한 공격을 통해서 학습데이터 중에서 모르는 데이터를 추가적으로 알 수 있다면 Privacy가 보장되지 않게 됩니다.
그래서 기존의 Database와 마찬가지로, 어떤 학습에 사용된 데이터들을 알고있을 때, 나머지 하나의 데이터를 알지 못하게 하는 것이 Privacy를 보장하기 위한 방법이 동일한 $(\epsilon, \delta)$-differential privacy 입니다.
Deep learning에 적용
Differential Privacy를 적용하기 위해서, SGD를 진행하는 과정에서 gradient를 일정 크기로 제한하는 Clipping을 진행하고, Gaussian noise를 추가하여 Gradient가 갖는 특징을 옅게 만드는 것입니다. 다음의 사진은 Differentially private SGD의 의사코드입니다.

SGD의 경우는 random sampling을 통해 dataset을 일부만 뽑아서 진행하기 때문에, 실제로는 $\epsilon, \delta$가 아닌 더 큰 값이 됩니다.
해당 과정으로 학습을 진행하였을 경우, $\epsilon, \delta$의 값에 따라서 학습률이 달라지게 되는데, 해당 결과는 다음과 같습니다.
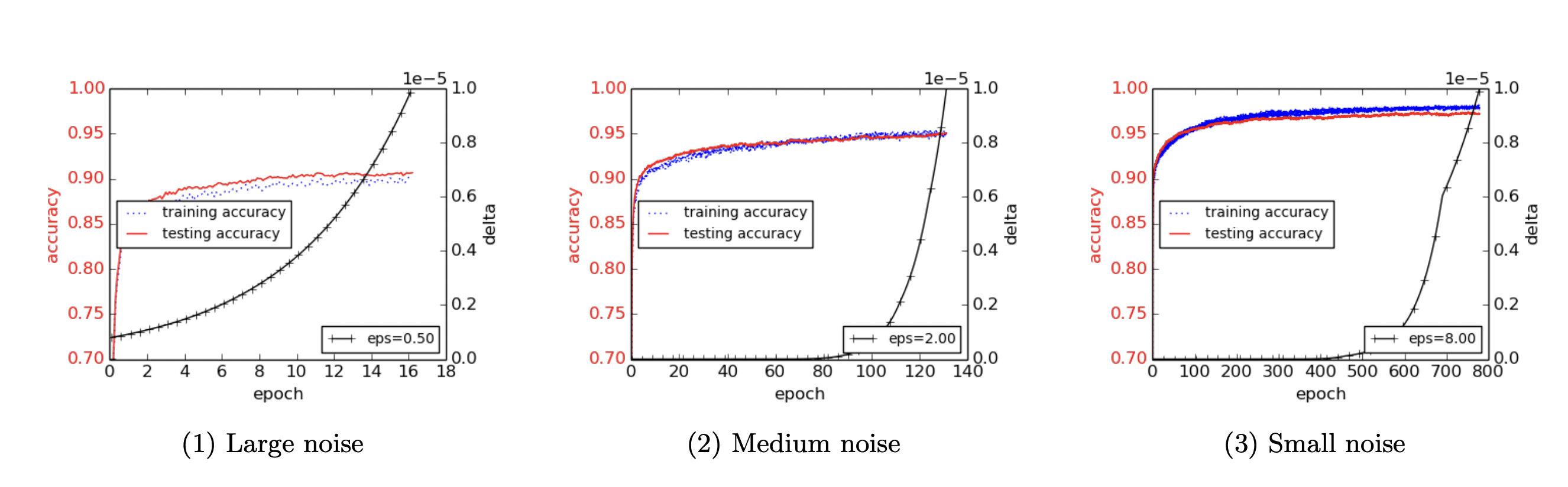
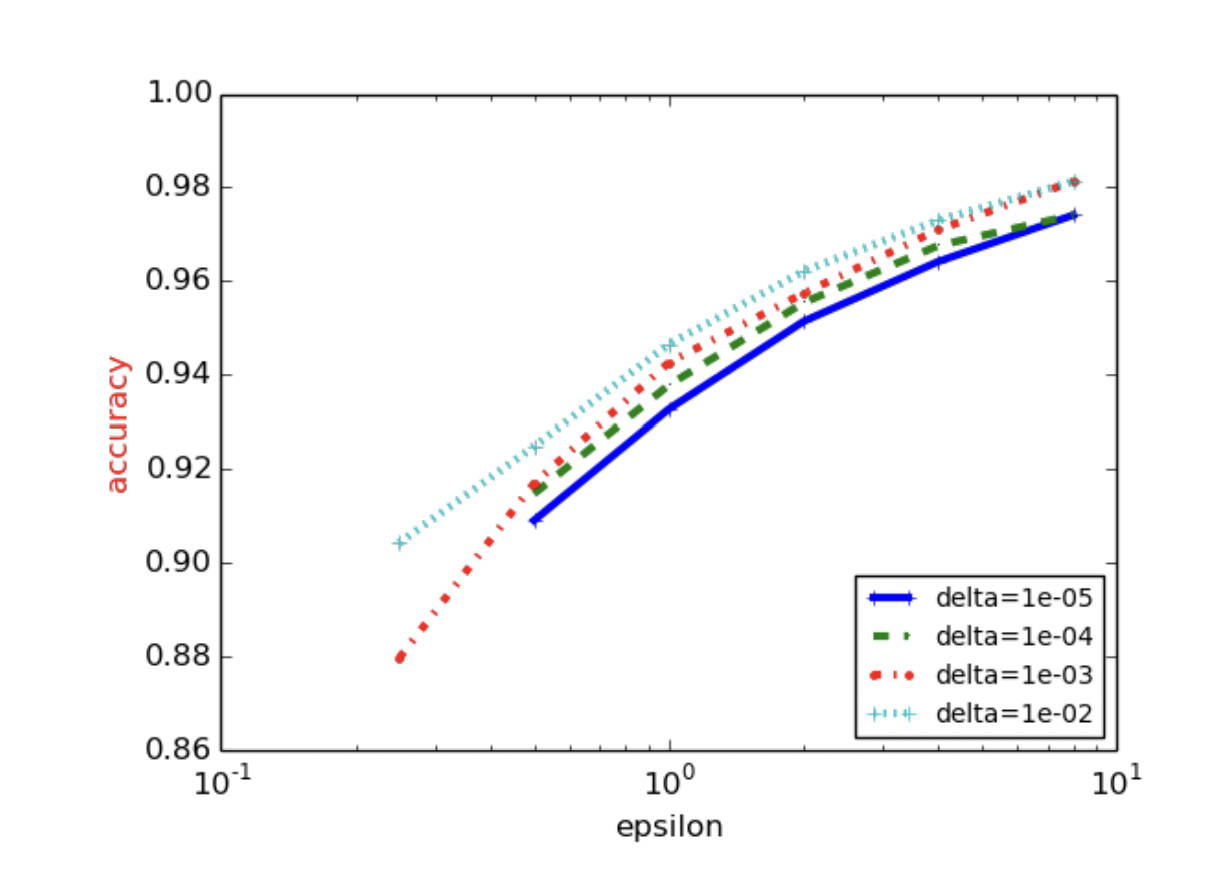
위에서 이야기하였듯이 당연한 이야기이지만, $\epsilon$이 작아질 경우 그만큼의 큰 노이즈가 들어간 것이기 때문에, 학습률이 떨어지는 모습을 볼 수 있습니다. 목표로 할 $\epsilon$과 학습률을 잘 조율한다면, 기존의 SGD보다 더욱 privacy하면서도 학습률은 떨어지지 않는 인공지능이 개발될 수 있습니다.
결론
차분 프라이버시라고 불리는 Differential privacy는 현재 여러 방면으로 사용되고 있습니다. Privacy를 위한 Split learning, 그리고 이를 활용한 SplitFed 등등 수많은 방식이 Differential privacy와 연관되고 있습니다. 정보를 사용하는 만큼, 그것을 보호하여야만 합니다. 이번에는 Dataset에서의 보안과 이것을 어떻게 측정하고 보장하는지에 대해 알아보았습니다. 다음에는 Federated Learning과 Split Learning, 그리고 그 둘을 응용한 SplitFed에 대해 조금 더 알아보고자 합니다.