ICPC World Finals 2021 풀이

algorithm , icpc , competitive-programming

11월에 ICPC World Finals 2021에 참가했습니다. 이후 11월 말까지 한 문제를 제외한 나머지를 모두 풀었고, 이 글에서 모든 문제의 풀이를 정리합니다.

최근 3년과 달리 상대적으로 쉬운 (플래티넘 하급 이하) 문제가 좀 더 많이 나왔는데, 그것들을 푸느라 더 어려운 문제에 쓸 시간이 부족했습니다.

A: Crystal Crosswind

바람의 방향이 $(w_x, w_y)$, 가장자리의 집합이 $S$라고 하면 다음과 같은 정보를 얻습니다.

(1) $(x, y) \in S$일 경우, $(x, y)$은 분자고, $(x - w_x, y - w_y)$는 빈칸입니다.
(2) $(x, y) \notin S$일 경우, $(x, y)$가 빈칸이거나 $(x - w_x, y - w_y)$가 분자입니다.

두 번째 조건은 “(2A) $(x, y)$가 분자면 $(x - w_x, y - w_y)$도 분자”, 혹은 “(2B) $(x - w_x, y - w_y)$가 빈칸이면 $(x, y)$도 빈칸”과 동치입니다.

먼저 분자가 가장 적은 경우부터 구해봅시다. 우선 (1)로부터 무조건 분자여야 하는 칸이 정해집니다. 그리고 (2A)로부터 추가로 무조건 분자여야 하는 칸이 어디인지 알 수 있습니다. (2A)를 반복적으로 적용시키다가 더 이상 무조건 분자여야 하는 칸이 안 생길 때가 바로 답입니다. 나머지 모든 칸을 빈칸으로 둬도 모든 규칙이 만족되기 때문입니다. 따라서 (2A)에 해당하는 각 칸 $(x, y)$에서 $(x - w_x, y - w_y)$로 간선을 긋고, (1)에 해당하는 칸들을 시작점으로 하여 그래프 순회를 해주면 됩니다. 이때 각 칸이 적어도 한 번 방문되었을 경우 그 칸에는 분자가 있고, 아니면 빈칸입니다.

분자가 가장 많은 경우도 비슷합니다. (1)로부터 무조건 빈칸이어야 하는 칸이 정해지고, 여기에 (2B)를 반복적으로 적용시켜야 합니다. 하지만 여기서 끝나는 게 아니라, (3) 격자의 바깥은 전부 빈칸입니다. 격자의 바깥에는 칸이 너무 많으니까 이걸 일일이 다 체크하지 말고, 여기다가 (2B)를 한 번 적용시켜서, 각 칸 $(x, y)$에 대해 $(x - w_x, y - w_y)$가 격자 바깥이면 $(x, y)$를 빈칸으로 두면 됩니다. 이제 (2B)에 해당하는 간선들을 긋고, (1)과 (3 + 2B)에 해당하는 칸들을 시작점으로 하여 그래프 순회를 해주면 됩니다.

시간 복잡도는 $O(d_x d_y k)$입니다.

B: Dungeon Crawler

시작점을 루트로 잡읍시다.

열쇠와 함정을 무시할 경우, 트리 순회를 하는데 가장 깊은 (루트에서 가장 먼) 점에서 멈추는 것이 최적입니다. 따라서 답은 2*(간선 길이의 합) - (가장 깊은 점의 깊이)입니다.

이제 함정과 열쇠가 있다고 합시다. 우선 함정이 열쇠의 조상이면 impossible입니다. 아닐 경우, 가장 마지막으로 방문하는 정점이 d라고 합시다. 가장 깊은 점이 아닐 수도 있습니다. 열심히 케이스 분석을 해보면서, 각 경로를 지나는 횟수를 아래 그림에서 빨간 글씨로 표시해보면 다음과 같습니다.

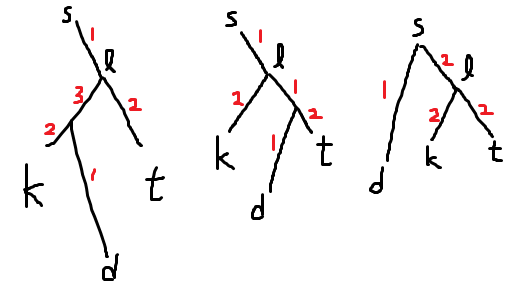
함정과 열쇠의 LCA를 $l$, 열쇠와 $d$의 LCA를 $z$라고 하면 답은 2*(간선 길이의 합) - (d의 깊이) + 2*(z에서 l까지 거리)입니다. 모든 $d$에 대해 이걸 계산하고 최솟값을 찾으면 됩니다.

쿼리를 같은 시작점들끼리 묶어, 각 시작점마다 $O(n)$ 시간 전처리를 한 번씩 해줄 수 있다고 합시다. 그 후 각 쿼리를 어떻게든 $O(n)$에 수행하면 $O(n^2 + qn)$이고, 이는 약 4억이므로 시간 내에 돌아갑니다.

저기서 시간이 걸리는 요인은 (1) LCA 계산, (2) 거리 계산입니다.

(1) LCA의 경우, 모든 정점과 열쇠의 LCA를 구하는 것이 문제입니다. LCA는 희소 배열 외에도 오일러 투어 + 구간 최솟값 쿼리로 풀 수 있음이 알려져 있습니다. 이 구간 최솟값도 범위의 한쪽 끝이 정해져 있기 때문에, 세그먼트 트리 같은 걸 쓸 필요 없이 그냥 범위를 하나씩 늘려 주면서 최솟값을 갱신하면 전체 $O(n)$에 모든 LCA를 구할 수 있습니다.

(2) 거리 계산의 경우, $z$와 $l$은 조상 관계이기 때문에 두 정점의 깊이의 차를 구하면 됩니다.

C: Fair Division

첫 번째 해적이 받는 금화의 비율은 $\sum_{i=0}^{\infty}(1-f)^{ni} = \frac{1}{1-(1-f)^n}$입니다. $(j+1)$번째 해적이 받는 금화의 비율은 $\frac{(1-f)^j}{1-(1-f)^n}$입니다. 따라서 금화의 비는 $1 : (1-f) : \cdots : (1-f)^{n-1}$입니다. $f = \frac{p}{q}$이고 $p$와 $q$가 서로소라고 하면, 금화의 비는 $q^{n-1} : q^{n-2}(q-p) : \cdots : (q-p)^{n-1}$입니다. 이 수들은 서로소이므로 $q^{n-1} + \cdots + (q-p)^{n-1}$의 합이 $m$의 약수여야 합니다.

그러려면 일단 $q^{n-1} \leq m$이어야 되는데, $n-1 \geq 5$이고 $m \leq 10^{18}$이기 때문에 $q \leq 3981$까지만 보면 됩니다. (1000이 아닙니다!) 오버플로우를 막으려면 저 $n$개 항을 통째로 합하는 게 아니라, 하나하나 더하면서 $m$을 넘을 때 바로 끊어줘야 합니다. 시간 복잡도는 $O(m^{2/(n-1)})$입니다.

D: Guardians of the Gallery

대회 당시 유일하게 아무도 못 푼 문제였고, 이 글을 쓰는 현재 백준 온라인 저지에 제출된 정답 코드가 없습니다. 아쉽게도 딱 한 테스트케이스에서 틀린 팀이 있었다고 합니다.

우선 조각상이 보이는 영역을 구해야 합니다. 조각상에서 각 꼭짓점으로 반직선을 긋습니다. 각 반직선에 대해, 그 반직선이 미술관의 어디까지 닿는지를 계산합니다. 간단하게 생각하면 반직선과 각 선분의 교점을 구하고 가장 가까운 교점을 구하면 되는데, 실제로는 반직선의 왼쪽과 오른쪽 영역이 모두 막히는 교점까지 가야 합니다. 예를 들어 아래 그림에서 A 방향으로 그은 반직선은 A에서 끝나는 게 아니라 오른쪽 영역까지 막히는 B까지 가야 합니다. 각 선분이 어느 방향에서 교차하는지를 구하고, 교점을 가까운 순으로 정렬한 다음 하나씩 확인하면 됩니다. 시간 복잡도는 $O(n^2)$이고, 이 다각형에는 변이 $O(n)$개 있습니다.

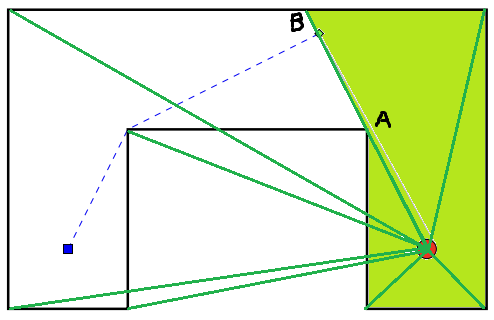
이제 출발점에서 목표 영역까지 가는 최단거리를 구해야 합니다. 최단경로는 다음과 같은 형태입니다. (1) 우선 미술관의 꼭짓점 몇 개를 거치고, (2) 마지막에 목표 영역의 한 변에 수직인 방향으로 직진합니다.

(1)은 출발점, 목표 영역의 꼭짓점 및 미술관의 꼭짓점들을 정점으로 잡고, 서로 이동 가능한 정점 쌍을 이어 그래프를 만든 뒤 데이크스트라 알고리즘을 돌려서 구할 수 있습니다. 정점 쌍이 서로 이동 가능한지 판별하려면 둘을 잇는 선분이 미술관의 각 변과 (끝점 제외하고) 안 겹치는지 판별하면 됩니다. 시간 복잡도는 $O(n^3)$입니다.

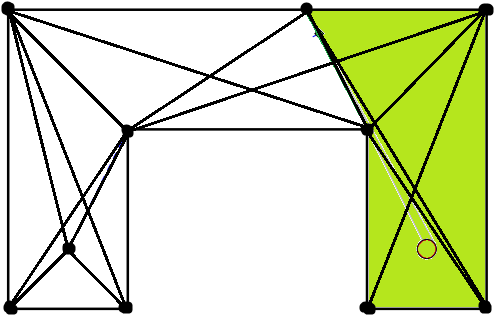
마지막으로, (2)는 각 정점에서 목표 영역의 각 변으로 수선을 긋고, 마찬가지로 미술관의 각 변과 안 겹치는지 + 수선이 실제로 그 변과 만나는지 판별하면 됩니다. 시간 복잡도는 $O(n^3)$입니다.

E: Hand of the Free Marked

우선 Fitch Cheney trick의 원본부터 분석해 봅시다. 이 마술은 본질적으로 52개 카드 집합에서의 크기 5의 조합에서 52개 카드 집합에서의 크기 4의 순열로 가는 일대일함수를 만드는 문제입니다. 조교는 조합에서 순열로 함수를 적용하고, 마술사는 그 순열에서 다시 조합으로 역함수를 적용하는 것이죠.

카드가 전체 $n$개이고 그중에서 $k$개를 뽑는다면, 전자는 $A := \frac{n!}{k!(n-k)!}$개이고, 후자는 $B := \frac{n!}{(n-k+1)!}$인데, $A \leq B$이면 일대일함수가 존재할 것 같이 생겼습니다. 계산해보면 $n = k!+k-1$일 때 정확히 $A = B$이고, $n$이 그보다 커지면 $A > B$라서 일대일함수가 존재할 수 없습니다. 물론 순열을 이루는 카드 4개가 모두 조합에 속해야 하기 때문에, $A \leq B$라고 해서 아무렇게나 일대일함수를 만들면 안 됩니다. 다행히도 조건을 만족하는 일대일함수가 항상 존재합니다. 왜냐?

전자와 후자를 잇는 이분그래프를 생각합시다. 카드가 많을 때 가능하다면 적을 때도 가능하니까, $n = k!+k-1$, $A = B$라고 합시다. 이제 이 그래프에 완전 매칭이 존재함을 홀의 정리로 증명합니다. 각 전자 조합은 정확히 $k!$개의 후자 순열과 인접하고, $A = B$니까 각 후자 순열도 정확히 $k!$개의 전자 조합과 인접합니다. 즉 이 그래프는 $k!$-regular graph입니다. 이제 전자 조합을 $s$개 골랐다고 하면, 이 조합들은 $k!s$개의 간선과 연결되어 있기 때문에, 적어도 $s$개의 후자 순열이 이 조합들과 인접해야 합니다. 따라서 홀의 정리에 의해 완전 매칭이 존재합니다.

$A > B$일 경우, 마술이 성공할 확률은 $\frac{B}{A}$입니다. 함숫값이 가능한 한 안 겹치도록 함수를 만들었으면, 전자의 원소 중에서 함수를 취하고 “역함수”를 취했을 때 자기 자신으로 돌아올 수 있는 원소가 $B$개이기 때문입니다.

이제 이 문제에서는 카드가 너무 많아서, ~~덱에서 카드를 몇 개 뺄 생각은 안 하고~~ 카드에 마킹을 해놓아서 마술사가 마지막 카드의 마킹을 알 수 있습니다. 얼핏 생각해보면 전자는 그대로 조합이고, 후자는 순열에다가 마킹 하나가 추가로 주어진 거니까 그대로 $A$와 $B$를 구하면 될 것처럼 생겼지만, 이러면 regular graph가 아니라서 위의 증명이 통하지 않습니다.

그 대신, 마술사가 마지막만이 아니라 모든 카드의 마킹을 알 수 있다는 사실에 주목합시다. 무슨 카드에 무슨 마킹이 있는지 외우면 그만이니까요. 따라서 마킹의 조합은 마술사와 조교가 공유하는 정보입니다. 그뿐만 아니라, 마킹의 조합을 고정하고 나면 원본 Fitch Cheney trick과 동일한 문제가 됩니다. 마킹의 조합을 백트래킹으로 뽑아내고, 각 조합에 대해 그 조합이 실제로 뽑힐 확률과 그 조합에서 마술이 성공할 확률을 곱하여 모두 더하면 답을 얻습니다.

마킹의 조합의 개수는 $m$과 $k$의 중복조합인데, $m=k=10$일 때 이는 $\binom{19}{10}=92378$이므로 충분히 모두 뽑아낼 수 있습니다. 이제 각 마킹 $i$에 대해, 그 마킹이 된 카드가 전체 $A_i$개이고 그중에서 $C_i$개를 뽑았다고 하면, 그 조합이 뽑힐 확률은 $\frac{1}{\binom{n}{k}} \prod \binom{A_i}{C_i}$이고, 그 조합에서 마술이 성공할 확률은 $\min(1, \frac{1}{\prod \binom{A_i}{C_i}} (k-1)! \prod \binom{A_i}{C_i} \sum_{C_i > 0} \frac{\binom{A_i}{C_i - 1}}{\binom{A_i}{C_i}})$ $= \min(1, (k-1)! \sum_{C_i > 0}\frac{C_i}{A_i - C_i + 1})$입니다.

저는 여기에 log를 씌워서 계산한 다음 exp로 되돌리는 식으로 구현했는데, long double도 안 되고 __float128까지 써야 $10^{-10}$ 정도의 절대오차로 통과했습니다. 모범 코드는 double만 쓴 걸로 봐서 식을 어떻게 정리했느냐에 따라 double로도 충분히 통과되는 것으로 보입니다.

시간 복잡도는 $O(\binom{m+k-1}{k}m)$입니다.

Fitch Cheney trick을 직접 선보이고 싶다면 이 문제와 이 문제를 풀어보시면 되겠습니다. 참고로 간선이 너무 많아서 이분 매칭 알고리즘을 직접 돌리는 식으로는 풀 수 없고, 매칭을 머리로 찾아내야 합니다.

F: Islands from the Sky

지문이 무서워 보이지만 (3차원 기하???), 정작 읽어보면 대부분이 지문을 무서워 보이게 만드는 장치라고 느껴집니다.

$\theta$에 대해 이분탐색을 합니다. $\theta$를 정하면 각 사다리꼴 영역이 정해집니다. 비행기의 높이가 $h$이면 밑변의 길이는 $2h \tan \theta$이고, 방향은 비행 경로를 90도씩 회전시켜서 구할 수 있습니다. 이제 각 섬이 적어도 한 사다리꼴의 내부에 속하는지 판별합니다. 사다리꼴은 볼록다각형이므로 섬의 모든 꼭짓점만 확인하면 됩니다.

시간 복잡도는 $O((\sum_{i=1}^n n_i) m\log X)$입니다.

저희 팀의 다른 팀원 분은 이분탐색 없이 풀었는데, 손 계산이 좀 들어갈 것 같습니다.

G: Mosaic Browsing

패턴과 격자의 높이가 1일 경우 와일드카드 문자열 매칭 문제와 동일하고, FFT로 풀 수 있습니다. 이 문제에서는 격자에 와일드카드가 없으므로 $T_j$는 안 곱해도 됩니다. 계수가 꽤 큰 편이므로 주의하세요.

높이가 2 이상일 경우, 그냥 격자를 일렬로 펴고 패턴에 와일드카드 패딩을 붙이면 높이 1 문제로 환원됩니다. 예를 들어 예제는 이렇게 될 겁니다. 물론 몇몇 인덱스는 격자에 안 맞기 때문에 매칭이 되어도 출력하지 말아야 합니다.

패턴: 1 0 0 0 0 1
격자: 1 2 1 2 2 1 1 1 2 2 1 3

bitset으로 푸는 방법도 있다고 합니다. (…)

H: Prehistoric Programs

AtCoder Beginner Contest 167F와 같은 문제이고, 다른 대회에서도 몇 번 나왔다고 합니다. 심지어 2016년 월드 파이널 Swap Space와도 거의 같은 문제입니다!

우선 주어진 문자열이 올바른 괄호 문자열인지 판별하는 문제를 생각해봅시다. PS를 입문할 때 접해보셨을 유명한 문제입니다. 문자를 차례대로 보면서 (이면 카운터를 1 증가시키고 )이면 1 감소시킬 때, 카운터가 단 한 번도 음수가 되지 않으면서 마지막에는 0이 되어야 합니다.

이제 이 문제로 돌아와보면, 각 조각은 다음과 같은 정보로 표현할 수 있습니다. “이 조각을 사용하려면 카운터가 $x$ 이상이어야 하고, 사용하면 카운터가 $d$만큼 변한다.”

모든 $d$의 합이 0이 아니면 당연히 impossible입니다. 이제 합이 0이라고 가정합시다. $d \geq 0$인 조각들을 올라가는 조각, $d < 0$인 조각들을 내려가는 조각이라고 합시다. 그러면 먼저 올라가는 조각이 다 나오고, 그 다음에 내려가는 조각이 다 나와야 합니다. 어떤 올바른 해에서 내려가는 조각 바로 다음에 올라가는 조각이 나왔다면 그 둘을 교환해도 여전히 올바른 해가 되기 때문입니다.

이 조건대로 나열하면 카운터는 올라가는 조각을 다 쓰면서 정점을 찍고 다시 내려가는 조각을 다 써서 0으로 돌아오게 됩니다. 그 정점을 기준으로 둘로 나누고, 내려가는 조각을 쓰는 과정을 뒤집으면, 올라가는 조각을 쓰는 과정만 두 번 있는 형태가 됩니다. 따라서 올라가는 조각만 쓰는 문제를 두 번 풀면 됩니다.

이제 올라가는 조각들을 잘 정렬해야 되는데, 그 순서는 바로 $x$에 대한 오름차순입니다. 어떤 올바른 해에서 $(x_1, d_1)$ 바로 다음에 $(x_2, d_2)$이 나오고 $x_1 > x_2$라면, $(x_1, d_1)$을 쓰는 순간에 카운터는 $c \geq x_1$인데, 둘을 교환하면 $c \geq x_1 > x_2$, $c + d_2 \geq c \geq x_1$이라서 여전히 올바른 해가 되기 때문입니다.

이렇게 정렬했는데도 올바른 괄호 문자열이 안 되면 impossible이고, 되면 그 순서를 그대로 출력해주면 됩니다.

I: Spider Walk

편의를 위해, 거미줄이 원형이 아니라 1번과 $N$번 가닥이 안 이어진 선형이라고 합시다. 풀이는 거의 달라지지 않습니다. 이제 우리가 풀어야 하는 문제는 다음과 같습니다.

사다리타기를 하는데, $i$번째 가닥에서 시작해서 $s$번째 가닥의 맨 밑에 도착하려고 합니다. 그어야 하는 다리의 최소 개수를 각각의 $i$에 대해 구하세요.

위에서 아래로 움직이면서 각 가닥으로부터 $s$번째 가닥까지 가는 게 아니라, 거꾸로 아래에서 위로 움직이면서 $s$번째 가닥으로부터 각 가닥까지 간다고 생각합시다.

DP[i][j]를, 첫 $i$개의 다리만 고려하고 나머지 다리를 자유롭게 그을 수 있을 때 $j$번째 가닥에 오는 최소 비용이라고 합시다. DP[0][..]은 $s$를 시작으로 양옆으로 하나씩 늘어나는 형태일 것입니다.

우선 DP[i][..]은 이웃한 DP 값들의 차이가 1 이하임을 염두에 둡시다. 이웃한 DP 값이 2 이상 차이가 날 경우, 낮은 쪽에서 높은 쪽으로 다리를 이어주면 더 좋은 해가 나오기 때문입니다.

DP[i][..]가 계산되었을 때 DP[i+1][..]을 계산하려면,

i번째 다리가 $a$와 $a+1$을 잇는다고 합시다.
DP[i+1][a+1]과 DP[i+1][a]에 각각 DP[i][a]와 DP[i][a+1]을 넣고, 나머지 DP[i+1][..] 값들은 DP[i][..]를 그대로 따라갑니다.
두 DP 값이 교환되면서 이웃한 DP 값의 차이가 2가 될 수 있습니다. 이 경우 높은 쪽을 하나 낮춰줍니다. 일단 DP[i+1][a]와 DP[i+1][a+1]만 낮춰줍시다.
그런데 저 값들을 낮추면서 또 다른 이웃한 DP 값의 차이가 2가 될 수 있습니다. 얘네들은 한꺼번에 낮춰줍시다. DP[i+1][a] = v라고 할 때, 각 DP[i+1][..]를 다시 계산합니다. DP[i+1][b]에는 현재 값과 v + (a에서 b까지의 거리) 중 최솟값을 넣으면 됩니다.
DP[i+1][a+1] = v'도 마찬가지로 써서 각 DP[i+1][..]를 다시 계산합니다.

여기까지 하면 $O(nm)$입니다.

네 번째, 다섯 번째 과정에서 DP[i+1][b]들을 효율적으로 계산해야 합니다. v + (a에서 b까지의 거리)는 절댓값 함수이기 때문에, 기울기가 1 또는 -1인 일차함수 여러 개로 표현할 수 있습니다. 따라서 이는 세그먼트 트리 lazy propagation으로 최적화할 수 있습니다. Lazy 값을 (p, q)로 둬서 min(현재 값, x+p, -x+q)을 표현하면 됩니다. 시간 복잡도는 $O(n + m \log n)$입니다.

이외에도 DP 값의 차이가 1인 이웃한 인덱스들을 그룹으로 묶어서 std::set으로 관리하는 풀이가 있습니다. 네 번째 과정에서 최대 하나의 그룹이 통째로 내려갈 것입니다. 따라서 내려갈 때 양옆의 그룹과 합쳐야 되면 합치고, DP 값을 교환할 때 그룹을 분리하는 식으로 구현할 수 있습니다.

J: Splitstream

우선 각 노드에 들어가는 수의 개수를 계산합니다. 1번을 입력으로 받는 노드는 정확히 $m$개의 수를 받습니다. Split 노드는 자신이 입력으로부터 받은 양을 두 출력 노드에 대강 반씩 나눠줍니다. 정확한 양은 자신에 들어가는 수의 개수의 홀짝성에 따라 다릅니다. Merge 노드는 출력 노드에 자신이 두 입력으로부터 받은 양 만큼 넘겨줍니다. 이 모든 것은 재귀 DP를 돌리거나, 위상 정렬하고 그 순서대로 DP를 돌려서 구할 수 있습니다.

쿼리를 처리하려면, $x$에서부터 입력 노드를 타고 거꾸로 거슬러 올라가면서 $k$를 관리하면 됩니다. 현재 보고 있는 입력이 split 노드의 출력일 경우 그 노드의 입력으로 올라가고, $k$는 대강 두 배가 됩니다. 정확한 양은 그 입력이 split 노드의 어느 방향 출력인지에 따라 다릅니다. Merge 노드일 때는 조금 복잡합니다. Merge 노드의 두 입력에 들어가는 수가 각각 $a$, $b$개라고 합시다. $k \leq 2 \times \min(a, b)$라면, $k$의 홀짝성에 따라 어느 입력으로 올라가는지가 다르고 $k$는 대강 절반이 됩니다. 아니라면, 둘 중 개수가 큰 입력으로 올라가고 $k$는 $\min(a, b)$만큼 감소합니다.

거슬러 올라가다가 한 번이라도 $k$가 현재 입력에 있는 수의 개수를 넘어가면 none이고, 넘어가는 일 없이 1번 입력까지 올라갔으면 그 $k$를 그대로 출력하면 됩니다. $O(qn)$인데 $q$와 $n$이 모두 작기 때문에 시간 내에 잘 돌아갑니다.

K: Take On Meme

각각의 밈은 벡터로 볼 수 있습니다. 노드 $v$의 최종 밈으로 가능한 모든 벡터의 집합을 $S_v$라고 합시다.

우선 벡터의 집합 $S$와 $T$에 대해,

$-S = {-p : p \in S}$, 즉 모든 벡터를 180도 뒤집은 집합,
$S + T = {p+q : p \in S, q \in T}$, 즉 두 집합에서 하나씩 뽑아 합치는 모든 경우를 담은 집합이라고 합시다. 이를 “집합의 덧셈”이라고 합시다. 마찬가지로 3개, $\cdots$, $k$개의 집합에 대해서도 덧셈을 정의할 수 있습니다.

이제 $S_v$를 다음과 같이 계산합니다.

리프 노드이고 해당하는 밈이 $p$일 경우, $S_v = { p }$입니다.
자식 노드가 $1, \cdots, k$라고 합시다. 어떤 $i$에 대해, $S_1, \cdots, S_k$ 중 $S_i$만 그대로 두고 나머지를 $-S$로 뒤집은 다음, 그 집합들을 전부 더한 것을 $T_i$로 정의합니다. 이제 $S_v = \bigcup_i T_i$입니다.

참 쉽죠? 아쉽게도 밈이 9,000개를 넘는데, 이러면 절대로 문제를 풀 수 가없으니 출제자가 치명적인 약점을 남겨 놨죠. 이 문제의 치명적인 약점은 바로 좌표 범위와 차수가 작다는 것입니다. 우리는 결코 이 문제를 포기하지도, 실망시키지도, 마음 바꿔 버리고 떠나지도 않을 겁니다.

사실 우리가 구해야 되는 건 $S_1$의 원소 중 원점에서 가장 먼 것입니다. 그러면 $S_v$의 원소를 다 들고 있지 말고, “원점에서 먼” 것들만 적당히 들고 있으면 되지 않을까요? 맞습니다. 각 벡터를 점으로 생각했을 때 볼록 껍질을 이루는 것들만 들고 있으면 됩니다. 그러니까 $S_v$는 그냥 벡터의 집합이 아니라 볼록다각형이라고 생각해도 충분합니다.

볼록다각형으로 생각하면 둘을 더하는 것도 간편합니다. 이를 민코프스키 합이라고 하고, 선형 시간에 구할 수 있습니다. 합집합은 그냥 볼록 껍질 알고리즘을 아무거나 쓰면 됩니다.

이렇게 하면 최적화가 매우 많이 된다는 건 짐작 가능하지만, 정확한 시간 복잡도를 구하기는 어렵습니다. 대충 어림잡아 봅시다.

좌표 범위가 $X$일 때 볼록 다각형의 점의 개수는 $O(X^{2/3})$임이 알려져 있습니다.
어떤 노드 $v$의 자식 노드가 $k$개이고, $v$ 서브트리 안에 리프 노드가 $f$개라고 하면, 좌표 범위는 $Xf$이므로 최종적으로 $O((Xf)^{2/3})$개의 점이 남고, 이는 $O(k \log k(Xf)^{2/3})$ 정도에 계산할 수 있습니다.
따라서 $S_1$은 $O(n \log k(Xn)^{2/3})$ 정도에 계산할 수 있습니다.
$n = 10^4, k = 100, X = 10^3$을 넣으면 약 32억이 나옵니다.
서브트리가 작을 때는 $O((Xn)^{2/3})$개보다 훨씬 적은 점이 쓰이고, 서브트리가 클 때도 매번 최악의 케이스가 나오는 건 불가능에 가깝기 때문에, 실제로는 32억보다 훨씬 적은 연산이 들 것임을 짐작할 수 있습니다. 이론적으로도 더 작은 상한을 얻는 게 가능할 것 같습니다.

실제로 돌려 보면 별다른 최적화를 하지 않아도 여유롭게 통과합니다. 제 구현은 약 200 ms가 걸립니다.

L: Where Am I?

각 시작점에서 출발했을 때 각 마커를 언제 방문하는지 계산합니다. 이 문제를 풀어보시면 좋습니다. $O(N^2M)$에 구할 수 있고, 사실 $O((NM)^2)$에 시뮬레이션 돌려서 계산해도 잘 짜면 시간 내에 돈다고 합니다. ($N$은 격자의 크기, $M$은 마커의 개수)

각 시작점마다 그 방문 시각들을 정렬합니다. 그 후 그 목록들을 다시 한 번 사전순으로 정렬합니다. 예를 들면 이런 식으로 나올 겁니다. (정확한 수는 아니고 그냥 아무거나 쓴 겁니다.)

[0, 1, 5, 10]: (1, 3)
[0, 1, 6, 7]: (2, 4)
[1, 5, 7, 12]: (3, 3)
[1, 5, 9, 13]: (4, 1)
[1, 7, 10, 12]: (2, 1)
[1, 9, 12, 15]: (4, 4)
...

(3, 3)과 (4, 1)을 처음으로 구별 가능한 시점은 7입니다. 6까지는 둘 다 마커를 1, 5에서 방문해서 서로 구별할 수 없지만, 7이 되면서 (3, 3) 쪽만 마커를 방문하기 때문입니다. 이를 일반화해보면, 목록이 $A$와 $B$인 두 지점을 구별 가능한 최초의 시점은 $A[i] \neq B[i]$인 가장 작은 $i$에 대해 $\min(A[i], B[i])$입니다.

이 비교 과정을 모든 목록으로 확장해봅시다. 시점 0이 되면 (1, 3)과 (2, 4)가 나머지 전부와 구별이 됩니다. 이제 재귀적으로 (1, 3)과 (2, 4)를 구별하고, 나머지 전부를 서로 구별하면 됩니다.

$solve(t, l, r)$을 현재 시각이 $t$일 때 $l$번째부터 $r$번째 목록까지 구별하는 함수라고 합시다. $l > r$일 경우 할 게 없습니다. $l = r$일 경우 $l$번째 목록이 시각 $t$에서 유일하게 결정됩니다. $l < r$일 경우, $l$번째 목록이 마커를 다시 방문하는 순간까지 시각을 올렸다가, 그 시각 $t’$에 마커를 방문하는 목록이 $l$부터 $k$번째라면, $solve(t’, l, k)$와 $solve(t’, k+1, r)$을 재귀적으로 호출해주면 됩니다.

출력할 때 $y$ 순으로 먼저 비교해서 정렬해야 한다는 점을 주의하세요.