Exploring Simulated Annealing for Derivative-free Optimization 1
Exploring Simulated Annealing for Derivative-free Optimization 1
현대 과학 및 수학에서, 많은 종류의 하이퍼파라미터를 갖는 문제의 최적의 솔루션을 찾는 것은 매우 중요한 문제입니다. 특히, 머신러닝, 딥러닝의 등장으로, 굉장히 어려운 형태의 최적화 문제의 좋은 솔루션을 구하는 것은 모델의 품질 향상과 밀접한 연관을 갖게 됩니다. 이 과정에서 다양한 종류의 optimizatino problem을 해결하게 되고, 그 과정에서 gradient 기반 접근 방법이 굉장히 많이 사용되고 있습니다.
그러나 최적화 문제 중에서는 특정 상태에 대한 gradient를 구하는 것이 어려운 문제들이 있습니다. 이러한 형태의 문제를 최적화하는 것을 Derivative-free Optimization, 혹은 Black Box Optimization이라고 부릅니다. 이러한 문제들의 경우, 현재 위치에 대한 gradient 기울기를 구하는 것이 불가능하기 때문에, 이전에 탐색한 좌표들의 결과값만을 가지고 최적점을 찾는 시도를 해야합니다.
이러한 derivatie-free optimization에는 다양한 종류의 접근 방법이 있습니다. 가장 기초적인 방법으로는 랜덤하게 주어진 좌표들을 탐색하는 Random Search부터, 다양한 종류의 휴리스틱 기반 기법들도 존재합니다.
본 글에서는 여러가지 접근 방법들 중, 자연에서 아이디어를 얻어 derivatie-free optimization에서 굉장히 좋은 성능을 내는 확률적 메타 휴리스틱인 Simulated Annealing에 대해 설명한다. Simulated annealing은 random search보다 평균적으로 압도적으로 좋은 성능을 보이며, 많은 종류의 함수에서 parameter 최적화가 되어있을 시 global optima에 가까운 점을 굉장히 빠르게 찾을 수 있다.
본 글에서는 이러한 simulated annealing의 기본적인 접근 방법부터, 최근에는 어떻게 더 향상되었는지에 대한 여러 동향에 대해 다룹니다.
Simulated Annealing의 거시적 해석
Optimization problem에서 가장 중요한 점은, 해당 상태에서 빠른 시간에 원하는 optimal point를 찾아내는 것입니다. 이 과정에서, Derviative를 사용할 수 있다면 특점 지점에서 시작하여 어느 수준의 local optimal point를 찾아내는 것은 크게 어렵지 않을 수 있습니다. 그러나 gradient를 사용하여 찾은 local optimal point의 경우, 가까운 neighbor point들에 비해서 더 좋은 상태를 가지기 때문에 해당 점을 탈출할 수 없고, 이로 인해 global optimal point를 찾는 것이 불가능할 수 있습니다.
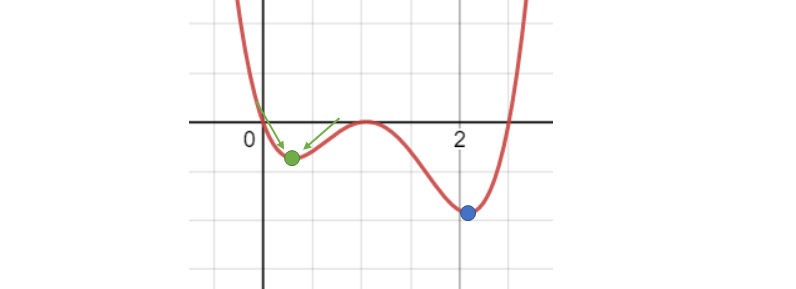
그 예시로 위 Fig 1을 살펴볼 수 있습니다. 해당 그림에서, 주어진 4차 함수의 global optimal point는 파란색 포인트이지만, 만약 우리가 gradient descent 등의 search를 사용하여 green point 왼쪽에서부터 찾기를 시작했다고 봅시다. 그러면 우리는 값이 더 작아지는 방향으로 이동하면서 초록색 포인트를 찾아내게 될 것입니다. 이 때, 초록색 포인트의 경우, 주변의 모든 가까운 점들이 자기보다 값이 크면서, gradient descent 방향이 초록색 포인트로 향한다는 것을 알 수 있습니다.
즉, 이러한 경우에 해당하는 초록색 포인트, local optimal point를 탈출하지 못하고 그대로 빠지게 된다는 것입니다. 특히 검색 공간이 불연속적이면서 볼록한 성질을 가지고 있지 않을 때에, 많은 방법론들은 이러한 local optimal point에 빠지는 경우가 강한 문제점이 있습니다.
이러한 문제가 존재해서, 만약 빠르게 local optimal point를 찾는 것이 아닌, 조금 더 시간이 걸리더라도 global optimal point에 가까운 점을 찾아내야하는 문제가 더 중요할 수 있습니다. 그러한 경우에 적용할 수 있는 방법이 바로 Simulated Annealing입니다.
Simulated Annealing의 경우, 재료의 물리적 특성을 변경하기 위해 재료를 가열하였다가 이를 냉각시키면서 변화시키는 Annealing을 모방한 휴리스틱 기법입니다. 재료를 가열 및 냉각할 때에 열역학적 자유에너지가 변화하는 것을 과정을 에너지와 확률에 기반하여 시뮬레이션하게 됩니다.
Simualted Annealing은 실제로는 Derivative를 사용할 수 있는 상태에서도 적용할 수 있으나, 현 post에서는 derivative-free optimization을 기준으로 설명하겠습니다.
Derivative-free optimization에 대한 기본적인 simulated annealing 구현 방법은 다음과 같습니다.
먼저, 최적화 지점을 찾기 위해 시작할 start point를 정합니다. 그리고 현재 포인트의 value를 recent solution으로 지정합니다.
그리고 나서, 해당 start point에서 가까운 지점, neighbor point를 정하여 해당 point의 value를 evaluate하여 new solution으로 지정합니다.
이렇게 찾은 new solution의 경우, 기존의 recent solution보다 더 좋을 수도, 혹은 더 나쁠 수도 있습니다. 이 때, 만약 new solution이 recent solution보다 더 좋은 지점이라면 항상 그 포인트로 이동하게 됩니다.
이 때, 문제는 new solution이 recent solution보다 더 안 좋을 경우입니다. Gradeint descent 등의 많은 방법론들은 우리가 찾은 지점이 주변의 다른 점들보다 더 좋을 경우, 해당 point를 탈출하기 어렵다는 점에서 문제를 겪었습니다. 그러나 simulated annealing의 경우, 이러한 현재의 new solution이 recent solution에 비해 얼마나 안 좋은가에 대한 정도를 확률적으로 evaluate하는 것으로, 해당 확률만큼 new solution을 채택할 것인지에 대해 결정합니다. 즉, 더 좋지 않은 방향으로도 이동할 확률을 만들어주는 것입니다.
이러한 형태의 알고리즘에서, 나쁜 솔루션을 수용하는 것으로 local optimal point를 탈출할 가능성을 주어 주어진 상태 전역을 찾아보는 것이 가능하게 만들어 더 광범위한 영역을 살펴볼 수 있도록 만들어줍니다.
그리고 이 과정에서, iteration이 증가하게 되어 많은 solution space를 탐색한 이후에는, 냉각 개념을 적용하여 갈수록 나쁜 솔루션을 채택할 확률을 감소시키게 됩니다. 이러한 개념은 많은 iteration 후에 도착한 지점이 global optimal point에 가까워지게 될 것이므로, 해당 영역을 탈출할 가능성을 낮추는 냉각 시스템이 됩니다. 이를 결정하는 요소로 온도 변수를 추가하게 되고, 초기 온도에서부터 0으로 점점 줄어들면서 냉각 상태로 변하게 만들어집니다.
Simulated Annealing의 미시적 해석
이제 실제로 Simulated annealing을 어떻게 구현하는지에 대한 자세한 내용들을 살펴보도록 하겠습니다.
Simulated annealing은 새롭게 찾은 recent state를 채택할 것인지에 대한 부분을 Boltzmann Distribution을 통해 결정합니다. 볼츠만 분포란, 특정 시스템이 해당 상태의 에너지와 온도의 함수로 특정 상태에 있을 확률을 확인하는 척도입니다. 이에 해당 분포는 다음과 같은 식으로 표현됩니다.
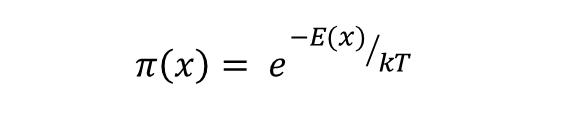
특정 상태를 x라고 한다면, 특정 상태 x에 대한 확률은 state x에 대한 에너지 E(x)를 볼츠만 상수 k와 현재 온도 T로 나눈 값에 음의 부호를 취한 값에 대한 exponential function으로 표현됩니다.
즉, 이 과정에서 에너지가 만약 높은 값을 가지게 된다면 해당 상태가 가질 수 있는 확률 또한 굉장히 작아지게 되며, 만약 상태가 낮은 에너지 준위를 가진다면 그 상태 또한 높은 확률을 가질 수 있게 됩니다.
이것이 실제 자연에서 사용되는 형태의 볼츠만 분포가 되며, simulated annealing에서도 위 식을 사용하여 확률을 구하게 됩니다.
Simulated Annealing에서 사용하는 식은 다음과 같습니다.
k번째 iteration을 통해 얻은 현재 point를 $x_{k}$, 그리고 해당 지점에서 찾은 새로운 neighbor point를 $y_{k}$ 라고 하겠습니다. 이 때에, 우리가 새로운 iteration에서 사용할 point $x_{k+1}$은 다음과 같은 과정을 통해 결정됩니다.
-
$p_{k} = exp(-\frac{E(y_{k}) - E(x_{k})}{kT_{k}})$
-
$x_{k+1} = \begin{cases} y_{k} \ with \ probability \ p_{k}
x_{k} \ with \ probability \ 1 - p_{k} \end{cases}$ -
$y_{k} \sim G(x, dy)$, when G is Markov kernel to generate a neighbor point
이 때, 정의되는 E(x)는 x state에 대한 objective function의 value입니다. 해당 objective function에 따라서 E가 결정되며, 이 때의 energy를 계산하기 위해 특별히 objective function이 수정될 수도 있습니다.
이를 통해서, 항상 energy potential이 최대한 낮아지는 상태가 더 좋은 상태로 놓게 된다면, 만약 새로운 state가 기존 state보다 더 낮은 energy를 가진다면 항상 probability가 1을 넘게 되어 새로운 상태로 채택하게 됩니다.
만약 그렇지 않다고 한다면, 볼츠만 분포에 따라서 선택된 확률 $p_{k}$에 따라서, 새로운 state를 채택하게 되거나 혹은 기존의 state를 그대로 유지하게 될 수도 있습니다.
이를 통해서 전체 N번의 iteration을 하게 된다면, 이 iteration 과정에서 살펴본 모든 x들 중에 가장 작은 objective function value를 가진 x가 simulated annealing을 통해 찾은 optimal point가 됩니다.
Simulated Annealing의 종류
Simulated Annealing 포스트는 두 차례에 걸쳐서 진행됩니다.
이번 포스트에서는 기존의 original SA의 동작 원리 및 방식, convergence 증명, 구현 방법에 대한 내용을 다루겠습니다. 다음 포스트에서는 이에 나아가 등장한 여러가지 advanced SA 기법들에 대해 정리할 예정입니다.
Original Simulated Annealing
기본적인 simulated annealing은 앞서 이야기한 것과 같이 볼츠만 분포 식을 이용하여 확률을 구하게 됩니다.
-
$p_{k} = exp(-\frac{E(y_{k}) - E(x_{k})}{kT_{k}})$
-
$x_{k+1} = \begin{cases} y_{k} \ with \ probability \ p_{k}
x_{k} \ with \ probability \ 1 - p_{k} \end{cases}$
위와 같이 정의한 식을 통해 구현하는 SA의 경우, 이들이 어떻게 수렴하는지, 그리고 temperature에 대한 부분을 어떻게 iteration에 따라서 변경할 것인지에 대한 정보가 필요합니다.
이를 구현하기 위해서 우리는 이를 정의할 필요가 있습니다.
기존의 SA에서 각 iteration이 진행되는 과정에서, 우리는 다음과 같은 수식들을 정의할 필요가 있습니다.
-
$P_{k}(x, dy) = p_{k}(y, x)G(x, dy) + (1 - r(x))\delta_{k}(dy)$, when P is Metropolis-Hastings kernel
-
$r(x) = \int_{X} p_{k}(y, x)G(x, dy)$
-
$μ_{k}(dx) = \mu_{k-1}P_{k}, \ \mu_{0} = (initial \ distribution)$
위와 같이 정의된 식이 있을 때에, 우리는 SA의 convergence를 정의할 수 있게 됩니다.
Convergence of SA
Under suitable ergodicity hypothesis on G, s.t.
- $T_{k} = \frac{(1+\xi)ΔE}{log(k + 2)}$
| then $ | \mu_{k} - \pi_{k} | \to 0$ and |
-
$\lim_{k \to \inf} \ \mu_{k}(S_{ϵ}) = 1, ϵ>0$
-
$S_{ϵ} = {x ∈ X, E(x) <= ϵ}$
위의 식들을 하나하나씩 살펴보도록 하겠습니다. 우리는 SA의 convergence를 보이기 위해서 Temperature T를 위와 같이 정의했습니다. 그리고 이 때에 함께 정의되는 S는 주어진 범위 X 내에서 에너지 준위가 특정 상수 ϵ보다 작거나 같은 것들만을 가지고 있는 level set을 의미하게 됩니다.
위에 해당하는 결과가 의미하는 바는 바로 주어진 μ가 확률 p를 추적하는 것이 가능해진다는 것을 말합니다. 우리는 μ와 p 모두 iteration을 거듭할 수록, 둘의 차이가 점점 0에 가까워진다는 것을 알 수 있습니다.
그 말인 즉슨, iteration이 반복되어 k가 무한으로 가는 과정에서, 주어진 μ의 경우 확률 p를 실제로 추적하는 것이 가능해지며, 이 과정에서 우리는 어떠한 임의의 양수 ϵ에 대해서도 항상 μ가 1로 가는 것을 살펴볼 수 있습니다. 이는 즉, 앞서 이야기한 것처럼 k가 무한으로 갈 수록, 굉장히 작은 ϵ에 대해서도 볼츠만 분포 $\pi$가 1이 되는 선택들을 할 수 있게 되면서 에너지 준위가 작아지는 (0이 되는)point를 선택하는 것이 가능해짐을 의미하고, 이는 곧 실제로 optimal solution인 $S_{*}$를 찾는 것이 가능해진다는 것입니다.
이러한 convergence가 보장되기 위해서 우리가 선택해야하는 Temperature decaying은 바로 위의 식처럼 iteration의 logarithm의 inverse에 해당하는 것을 선택하면 가능하다는 것이 보장됩니다.
SA - example
Rosenbrock Function
Rosenbrock function이란 수학적 최적화에서 최적화 알고리즘을 실험해볼 용도로 만들어진 비볼록 함수입니다. 식은 다음과 같이 표현됩니다.
- $f(x,y) = (a - x)^{2} + b(y - x^{2})^{2}$
이러한 그래프를 그려보면 기본적으로 길고 좁은 포물선 모양의 골짜기가 나오게 됩니다. 그렇기 때문에, 알고리즘이 골짜기를 찾아내면서 그 중에서도 최적의 값을 찾아내는 것을 목표로 합니다.
이 과정에서, 골짜기를 찾아내는 것은 쉬우나, 그 골짜기 중에서 global optimal point를 찾아내는 것은 어렵기 때문에, 얼마나 잘 찾아내는지에 대한 여부를 확인할 때 사용하게 됩니다.
우리는 실제 Simulated annealing을 다음과 같은 함수에서 적용하면서, 각 iteration 별로 찾아내는 optimal point의 value들과, 그 위치에 대해서 확인해볼 예정입니다.
하이퍼파라미터는 다음과 같습니다.
- max_iteration: 전체 iteration 수
- bc: 볼츠만 상수
- T: Temperature
- a, b: rosenbrock function 변수
- r: neighbor point 찾을 반경
위 configuration에서의 최적의 값은 0이며, x와 y 모두 1일 때가 최소입니다.
아래 코드에서 하이퍼파라미터를 변경하여 실행할 수 있습니다.
실행 결과에서 E와 A를 바꾸어, 주어진 함수를 다양한 각도에서 확인할 수 있습니다.
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from ipywidgets import interactive
import random
import math
def rosenbrock(x, y, a = 1, b = 100):
return (a - x)**2 + b*((y - x**2)**2)
a = 1
b = 100
r = 0.1
bc = 10
T = 1
seed = 1
max_iteration = 100
f = rosenbrock
random.seed(seed)
x1 = np.linspace(-2, 2)
x2 = np.linspace(-1, 3)
X1, X2 = np.meshgrid(x1, x2)
F = rosenbrock(X1, X2, a, b)
x = [-2.0, -1.0, 2.0, 3.0]
y = [-2.0, 2.0, -2.0, 2.0]
X = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
Y = [[[0 for _ in range(4)] for _ in range(4)] for _ in range(max_iteration + 1)]
best = [20000, 20000, 20000, 20000]
best_point = [(10, 10), (10, 10), (10, 10), (10, 10)]
def G(x, y, r):
a, b = random.uniform(-r, r), random.uniform(-r, r)
return x+a, y+b
def sa_p(E, bc, T):
return np.exp(-(E / (bc * T)))
def plotter(E, A):
global X, Y
fig = plt.figure(figsize = [12, 8])
ax = plt.axes(projection='3d')
ax.plot_surface(X1, X2, F, cmap='jet', alpha=0.8)
ax.view_init(elev=E, azim=A)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('F(X, Y)')
for i in range(4):
ax.scatter(X[max_iteration][0][i], Y[max_iteration][0][i], f(X[max_iteration][0][i], Y[max_iteration][0][i], a, b), color = 'red')
for i in range(4):
for j in range(4):
X[0][i][j] = x[j]
Y[0][i][j] = y[j]
for k in range(max_iteration):
T = 1 / math.log(k+2)
for j in range(4): #SA
x, y = X[k][0][j], Y[k][0][j]
nx, ny = G(x, y, r)
fx = f(x, y, a, b)
fy = f(nx, ny, a, b)
if fy < best[0]:
best[0] = min(best[0], fy)
best_point[0] = (nx, ny)
p = sa_p(fy - fx, bc, T)
now = random.uniform(0, 1)
if now < p:
X[k+1][0][j], Y[k+1][0][j] = nx, ny
else:
X[k+1][0][j], Y[k+1][0][j] = x, y
print('iteration %d - best score: %f / point (x, y) = (%f, %f)'%(k, best[0], best_point[0][0], best_point[0][1]))
print('\n\nlegend\n')
print('SA - red point')
iplot = interactive(plotter, E = (-20, 90, 5), A = (-20, 90, 5))
iplot
위 코드는 실제 python을 통해서 실행해볼 수 있습니다.
주어진 코드가 task에 맞춰서 최적의 하이퍼파라미터 튜닝이 되어있는 상태는 아닙니다.
이에 대해 위 조건으로 4개의 initial point에서 100회의 iteration으로 찾은 실제 결과값 및 생성된 그래프는 다음과 같습니다.
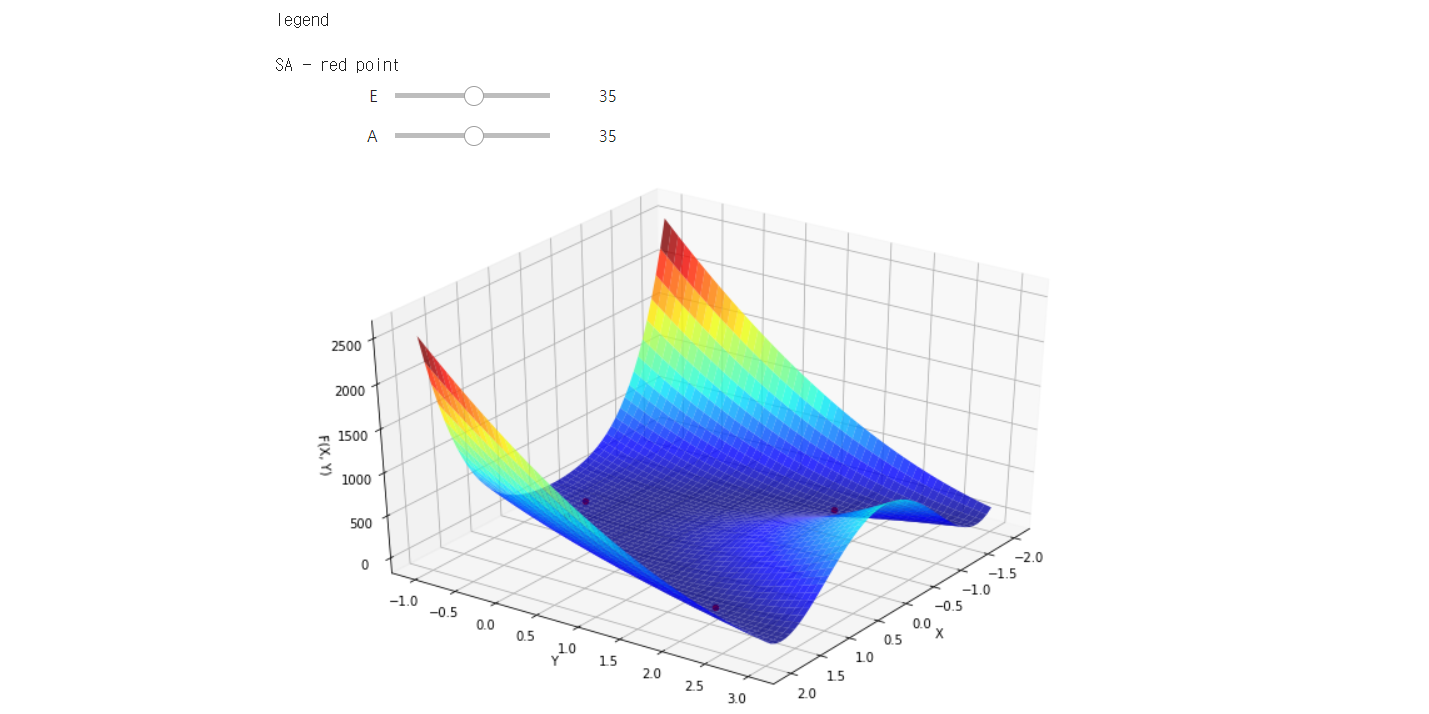
마치며
이 post에서는 derivative-free optimization problem에서 최적화하기 위한 휴리스틱 기법인 Simulated Annealing에 대해 다루었습니다.
가장 기본적인 형태의 SA에 대해 다루고, 이러한 optimization 기법들의 성능을 측정하기 위한 함수인 rosenbrock function에 대한 내용을 다루어 기본적인 최적화와 관련된 내용을 설명하였습니다.
다음 포스트에서는 이를 최적화하기 위해 나온 여러가지 아이디어들인 FSA, SMC-SA, 그리고 가장 최근에 발표된 논문들에 대해 다루면서, SA 기법을 최적화하기 위해 어떠한 방식의 접근들이 있었는지 이야기해보도록 하겠습니다.
Related Paper
2. D Bertsimas, et al. Simulated annealing. Statistical Science, 1993.