A Tree Representation for Failure Function of a String
A Tree Representation for Failure Function of a String
Introduction
KMP(Knuth-Morris-Pratt) 알고리즘은 주어진 문자열에서 패턴 문자열을 검색하는 전통적인 선형 시간 알고리즘이다. 알고리즘 대회 분야에서도 KMP 알고리즘을 응용하여 해결할 수 있는 문제는 꾸준히 출제되고 있으며, 한국 리저널만 보더라도 2017 Preliminary J번, 2021 Regional K번 등에서 등장한 바가 있다.
KMP 알고리즘을 응용하여 해결하는 문제들은 많은 경우 KMP 알고리즘의 중간 단계에서 등장하는 실패 함수(Failure function)에 대한 깊은 이해를 바탕으로 한다. 따라서, 실패 함수가 해당 문자열의 구조에 대해 어떤 점을 시사하는 가에 대해서 궁금증을 가지는 것이 자연스럽다.
이 글에서는 실패 함수의 성질과 이로부터 자연스럽게 파생되는 트리 구조에 대해서 설명한다. 실패 함수의 정의와 이를 $\mathcal{O}(N)$ 시간에 계산하는 방법을 미리 알고 있다는 가정 하에 설명한다.
Graph Representation
문자열 $S = ‘‘abcababcb’’$ 가 주어진 상황을 생각하자. 이때 $S$의 실패 함수는 $F = [0, 0, 0, 1, 2, 1, 2, 3, 0]$과 같이 계산된다.
실패 함수를 계산하는 과정을 되살펴보면, $F$의 각 원소는 $S$의 어떤 두 문자가 같은 지에 대한 여부를 알려준다. 정확히는, 다음과 같은 정보가 모든 $i$에 대해서 주어진다.
- $S[i]$는 $S[F[i - 1]]$ 과 같지 않다.
- $S[i]$는 $S[F[F[i - 1] - 1]]$과 같지 않다.
- $\cdots$
- $S[i]$는 $S[F[\cdots [F[i - 1] - 1] \cdots ]- 1]]$ ($= S[F[i] - 1]$)과 같다.
앞의 예시에서, $i = 5$인 경우 $S[5]$는 $S[F[4]] = S[2]$와 같지 않고, $S[5] = S[0]$과 같다는 정보가 얻어진다.
그리고, 우리가 실패 함수만을 보고 알 수 있는 정보는 이게 전부라는 사실도 알 수 있다. 왜냐하면 이 정보들은 실패 함수를 계산할 때 $S$의 원소 사이에 일어나는 모든 비교를 나열한 것 뿐이라, 이 정보만 가지고 실패 함수를 역으로 얻어낼 수 있기 때문이다.
다시 말해, 실패 함수가 주는 정보를 다음과 같이 정리할 수 있다.
- 몇 개의 쌍 $(i, j)$에 대하여 $S[i] = S[j]$.
- 몇 개의 쌍 $(i, j)$에 대하여 $S[i] \neq S[j]$.
| 각각을 $ | S | $개의 정점을 가진 그래프에서의 간선이라고 생각하면, 실패 함수가 주는 정보를 두 가지 종류의 간선을 가진 그래프로 생각할 수 있다. |
Recursive structure
실패 함수에 대응하는 그래프 표현을 찾았으니, 이제 모든 그래프에 대해서 대응하는 실패 함수가 존재하는 지 물어볼 수도 있겠다. 그런데 조금만 생각해보면 이는 사실이 아님을 알 수 있다.
예를 들어, $S[i] = S[j]$, $S[j] = S[k]$, $S[i]\neq S[k]$ 와 같이 간선이 형성되어 있는 경우 조건을 만족하면서 $S[i], S[j], S[k]$의 값을 결정하는 것이 불가능하다.
이는 우리가 구성한 그래프가 실패 함수의 구조를 온전히 담아내지 못하고 있다는 뜻이 된다. 즉 더 좋은 표현이 존재할 수도 있다는 가능성을 제공한다. 하나의 여지는 이 그래프가 실패 함수의 다음 재귀적인 구조를 전혀 반영하고 있지 않다는 것이다.
- $i \rightarrow \underline{F[i - 1]} \rightarrow F[\underline{F[i - 1]} - 1] \rightarrow \cdots$
이런 구조를 반영해서, 다음과 같이 구성된 그래프를 생각한다.
- 각 $i$에 대해서, $i$에서 $F[i - 1]$로 가는 방향 간선이 존재함
이때 $0\leq F[i - 1] < i$이 항상 성립하므로, 이 그래프는 정확히 $0$번 정점을 루트로 하는 트리 구조를 가진다. 이때 앞서 설계한 그래프의 간선들은 이 트리에서는 각 정점 $i$에 대해 방향 간선을 따라 올라가면서 어느 시점 이전까지 만나는 점들을 $i$랑 이어주는 형태로 나타난다.
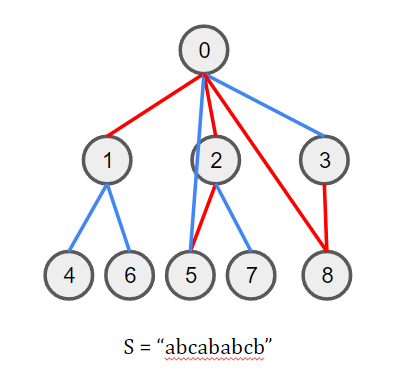
$S[i] = S[j]$인 관계를 파란색 간선, $S[i] \neq S[j]$인 관계를 빨간색 간선으로 표현하였다.
Tree structure
그래프를 트리 위에 올려놓고 보면, 다음 사실을 관찰할 수 있다.
- 각 정점 $i$에 대해서, 방향 간선을 타고 올라가면서 만나는 모든 정점들의 집합을 $V_i$라고 하자. $V_i$의 각 원소 $j$에 대해서, $S[i]$는 $S[j]$랑 반드시 다르거나, 반드시 같아야만 한다.
$0$번 정점을 만나거나 $S[i] = S[j]$인 $i$의 조상 $j$을 찾을 때까지 계속해서 빨간색 간선이 추가되므로, 이 사실을 이용하여 귀납적으로 증명할 수 있다. $V_j$의 각 정점들에 대해서 $S[j]$와 값이 같은 지의 여부가 귀납 가정에 의해 알려져 있으므로, $S[j] = S[i]$임에서 $V_i$에 속하는 모든 정점들에 대해 $S[i]$와 같은 지의 여부를 알 수 있다.
이제, 파란색 간선들로 이어진 정점들의 컴포넌트를 생각하면, 해당 정점들은 모두 값이 같아야 한다. 또한, 조상-자손 관계에 속하는 모든 두 정점의 값이 같은 지의 여부가 정해지므로, 해당 컴포넌트에 속한 정점 중 가장 루트와 가까운 정점만을 남겨도 잃는 정보가 없다는 사실을 알 수 있다.
약간의 설명을 덧붙인다.
- 각 컴포넌트에서 루트와 가장 가까운 정점 $v$는 유일하다. 모든 파란색 간선이 조상-자손 관계에 속한 점 쌍을 잇기 때문에, 해당 컴포넌트의 모든 정점은 $v$의 서브트리에 속해야만 한다.
- 어떤 정점 $x$가 해당 컴포넌트에 속한 어떤 정점과 조상-자손 관계에 있다면, $x$는 $v$와도 조상-자손 관계에 놓여 있다. 따라서 $v$가 아닌 해당 컴포넌트의 다른 정점들은 $v$가 주는 정보보다 더 많은 정보를 제공하지 않는다.
따라서 이 사실을 바탕으로 트리를 다음 그림과 같이 압축할 수 있다.
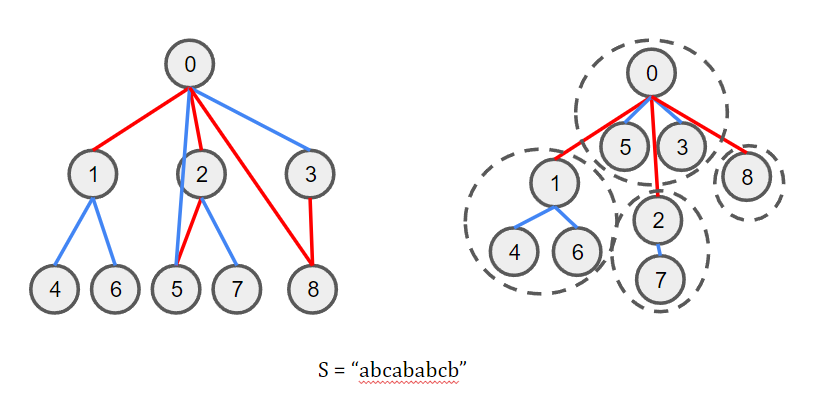
오른쪽 그림에서 점선으로 구분된 구역 안의 점은 파란색 간선들로 연결되어 있는 정점들이다. 이제 이 트리에 유일하게 남아있는 조건은 다음과 같다.
- 각 점선 구역 내부의 점들에 대해서 $S[i] = S[j]$가 성립한다.
- 조상-자손 관계에 놓여있는 두 점선 구역에 대해서 $S[i] \neq S[j]$가 성립한다.
Conclusion
실패 함수에 대한 논의에서 위 트리를 만드는 것만으로도 할 수 있는 얘기가 있다. 실패 함수가 주어졌을 때의 원본 문자열들에 대한 질문은, 위의 트리에서 조상-자손 사이의 색깔이 전부 다른 색칠에 대한 질문으로 환원할 수 있다. 이는 복잡한 문자열 문제를 트리와 연관지어 생각할 수 있는 좋은 도구가 된다.
| 대표적으로 주어진 실패 함수에 대한 가능한 원본 문자열의 개수를 묻는 질문은 가능한 색칠의 개수를 묻는 문제로 환원할 수 있고, 이는 각 정점마다 $ | \Sigma | - depth$ 를 곱하는 것으로 쉽게 해결할 수 있다. |
애석하게도 정점에 번호가 존재하는 임의의 트리를 가져왔을 때, 해당 트리에 대응하는 문자열이 존재하는 것은 아니다. 이는 여전히 해당 구조가 실패 함수의 구조를 완벽히 담고 있지 않다는 것을 의미하고, 문자열의 suffix structure과 연관이 되어있는 것으로 보인다. suffix automaton과 같은 해당 구조에 대한 좋은 표현법들과 같이 이해한다면 문자열 문제를 해결하는 좋은 도구를 얻을 수 있을 것이라고 생각된다.
Addendum
본문의 내용을 이용하여 다음 문제를 쉽게 해결할 수 있다.