A Bayesian Perspective on Federated Learning (2)

Introduction

지난 글에서는 FL을 probabilistic inference problem으로 볼 수 있다는 관점을 제시한 FedPA 알고리즘에 대해서 살펴보았습니다. FedPA는 FL에서 주로 발생하는 local device overfitting 문제를 해결하기 위해 Bayesian 방법론을 적용하였습니다.

이번 글에서는 local device에서 빈번히 발생하는 overfitting 문제가 아닌, server에서 aggregation 시 발생하는 문제를 Bayesian 방법론을 적용하여 완화한 FedBE 알고리즘을 소개해보려고 합니다.

FedAvg

본 논문 또한 지난 글의 FedPA와 유사하게 FedAvg의 문제점을 제시하고 그를 Bayesian 방법론으로 완화한 논문입니다. FedAvg가 어떤 것인지는 다루지 않고 FedAvg가 가지는 문제점들에 대해서만 짚고 넘어가겠습니다.

Communication bottleneck

FedAvg에서는 일반적으로 각 round 마다 수행되는 communication이 bottleneck입니다.

communication bottleneck을 해결하기 위해서, 각 round에 client에서 더 많은 local computation (more local SGD steps)을 수행해서 round 수를 줄이고 학습 속도를 높일 수 있습니다. 하지만 local computation을 많이 수행할수록, client data heterogeneity (non-IID)에 의해 global model이 inferior model로 수렴하는 문제가 발생합니다.

이러한 문제를 Bayesian 방법론을 적용하여 완화한 논문이 FedPA였습니다.
Model aggregation: element-wise averaging

FedAvg에서는 local model들의 weight들에 element-wise average를 취하여 하나의 global model로 aggregation합니다.

이때 user들이 iid data를 가지고 있다는 가정 하에서, FedAvg는 ideal model에 수렴하는 것이 밝혀졌습니다. 여기서 ideal model은 각 user들의 data를 모두 통합하여 centralized하게 학습된 모델을 의미합니다.

다만 user들이 iid data를 가지고 있다는 가정에서 멀어질수록, FedAvg는 ideal model로부터 멀어집니다. weight space 상에서 permutation-invariant property를 가지는 over-parameterized model에서는 element-wise averaging을 취하는 것은 오히려 역효과를 낼 수 있기 때문입니다.

추가로 FedAvg는 user들 간의 variances 등의 user들 간의 정보를 활용하지 못한다는 문제가 있습니다.

FedBE에서는 이러한 aggregation 방식의 문제점을 완화하기 위해 Bayesian 방법론을 도입하였습니다.

Bayesian model ensemble

본 논문에서는 기존 aggregation 방식의 문제점을 완화하기 위해, Bayesian inference를 사용하는 새로운 aggregation 방식을 제안합니다. 여기서 사용되는 bayesian inference란, 하나의 model을 사용하는 single point estimation에 의존하는 것이 아니라, 가능한 모든 model들의 output들을 통합하는 것을 의미합니다.

다시 말해, $p(w|D)$ 가 global model의 posterior distribution이고, $p(y|x, w)$ 가 global model $w$ 의 output probability라고 할 때, global model의 posterior distribution $p(w|D)$에서 가능한 global model을 모두 뽑아서 그에 대한 output probability $p(y|x, w)$ 들을 통합하여 최종 output probability를 구한다는 뜻입니다. 식으로 나타내면 아래와 같습니다.

\[p(y\|x, D) = \int p(y\|x, w) \cdot p(w\|D) dw\]

이때 global model의 posterior distribution $p(w|D)$에서 가능한 global model을 모두 뽑는 과정이 불가능하기 때문에, Monte Carlo method로 $M$개의 model들을 sampling하여 그것들로 model ensemble을 형성합니다.

\[p(y\|x, D) \approx {1 \over M} \Sigma_{m=1}^M p(y\|x, w^{(m)}), \ \ where \ \ w^{(m)} \sim p(w\|D)\]

여기서 2가지 문제가 발생합니다.

첫 번째로 global model을 sampling할 distribution $p(w|D)$ 을 어떻게 구할 것인가에 관한 문제가 있습니다.

두 번째로는 server에서 하나의 global model만을 client들에게 보내야 하기 때문에 Bayesian model ensemble을 바로 FL 환경에 적용할 수 없다는 문제가 있습니다. 따라서 Bayesian model ensemble의 prediction rule을 하나의 global model로 변환해야 합니다.

Constructing global model distribution $p(w|D)$

$g_i := -(w_i - \bar w)$ 라고 하면, $w_i = \bar w - g_i$ 가 됩니다.

그럼 $g_i$ 를 minibatch $D_i \subset D$ 에서의 $K$-step stochastic gradient 라고 볼 수 있습니다. 즉, 각 local model들을 $\bar w$ 로부터 $K$-step SGD를 거친 결과물들로 여기는 것입니다.

이러한 관점에서 본 논문에서는 $\bar w$, $w_i$를 이용해서 global model distribution $p(w|D)$를 근사하였습니다.

논문에서는 먼저 $p(w|D)$가 아래와 같은 가우시안 분포라고 가정하였습니다.

\[w^{(m)} \sim N(\mu, \Sigma) \\ where \quad \mu = \Sigma_i {\|D_i\| \over \|D\|} w_i, \quad \Sigma = \Sigma_i {\|D_i\| \over \|D\|}(w_i - \mu)^2\]

위 분포를 활용해서 우리는 model ensemble을 위한 $M$ 개의 model을 samping 할 수 있습니다.

\[{\{w^{(m)} \sim N(\mu, \Sigma)\}}_{m=1}^M\]

다음으로 논문에서는 $p(w|D)$가 아래와 같은 디리클레 분포를 따른다고 가정하기도 했지만, 대부분의 경우 가우시안 분포라고 가정한 것이 더 좋은 성능을 보였습니다. 이 방식은 비교적 단순하고 직관적이지만, client들 간의 variance를 고려해줄 수 있다는 점에서 단순히 $\bar w$ 를 쓰는 방식과 큰 차이가 있습니다.

Knowledge distillation

앞서, Bayesian model ensemble을 FL 환경에 적용하기 위해 server에서 Bayesian model ensemble의 prediction rule을 하나의 global model로 변환해야 한다는 문제점이 있었습니다. 본 논문에서는 Bayesian model ensemble $p(y|x, D)$의 prediction rule을 $\bar w$ 에 transfer하는 방식을 사용합니다.

일반적으로 Knowledge Transfer은 크게 Knowledge Distillation과 Transfer Learning으로 구분 가능한데, Transfer Learning은 주로 서로 다른 도메인에서 지식을 전달하는 과정에서 사용되며, Knowledge Distillation은 Model Compression 등과 같이 주로 같은 도메인 내에서 하나의 모델의 지식을 다른 모델로 전달하는 과정에서 사용됩니다.

본 논문에서도 이론적으로는 무한 개의 model로 이루어진, 실제로는 sampling된 $M$ 개의 model로 형성된 Bayesian model ensemble의 지식을 $\bar w$ 에 전달하기 위해, Knowledge distilllation 과정을 거칩니다.

본 논문에서는 server가 unlabeled data에 접근할 수 있다고 가정하였는데, 이 가정에 대한 근거를 아래와 같이 들었습니다.

server는 주로 model validation을 위해 자신만의 data를 가지고 있음
- 예를 들어 자율 주행 시스템의 경우 고객의 data를 수집하는 것이 아니라 직접 data를 생산할 수 있음
unlabeled data는 labeled data에 비해 수집하기가 쉬움

참고로 본 논문에서는 CIFAR-10, CIFAR-100, Tiny-ImageNet에 대해서 실험을 진행했는데, 2000개의 unlabeled data만으로도 FedAvg에 비해 충분한 성능 향상이 있었습니다. 이는 기존 dataset의 2~4% 정도 수준입니다.

Bayesian model ensemble $p(y|x, D)$의 prediction rule을 transfer하기 위해, server의 unlabeled data에 대한 Bayesian model ensemble의 prediction을 pseudo-label로 붙혀 생성된 dataset을 바탕으로 $\bar w$ 를 학습시킵니다.

이때 Bayesian model ensemble의 성능이 ideal model의 성능에 비해 좋지 못할 것이기 때문에 pseudo-label은 실제 label과 차이가 있을 것입니다. global model이 이런 noisy한 dataset에 over-fitting되는 것을 막기 위해 $\bar w$ 학습 시에 SWA를 적용합니다. 이로써 Bayesian model ensemble의 prediction과 유사한 prediction을 수행하도록 학습된 $\bar w$ 가 새로운 global model이 되고, 이 model이 다시 client들에게 전달되어 새로운 round를 시작합니다.

SWA

SWA은 간단하게 말하자면 model을 시간축으로 ensemble하는 알고리즘으로, 일정 시간 단위로 model의 weight들을 sampling해서 average를 취함으로써 간단하게 구현할 수 있습니다.

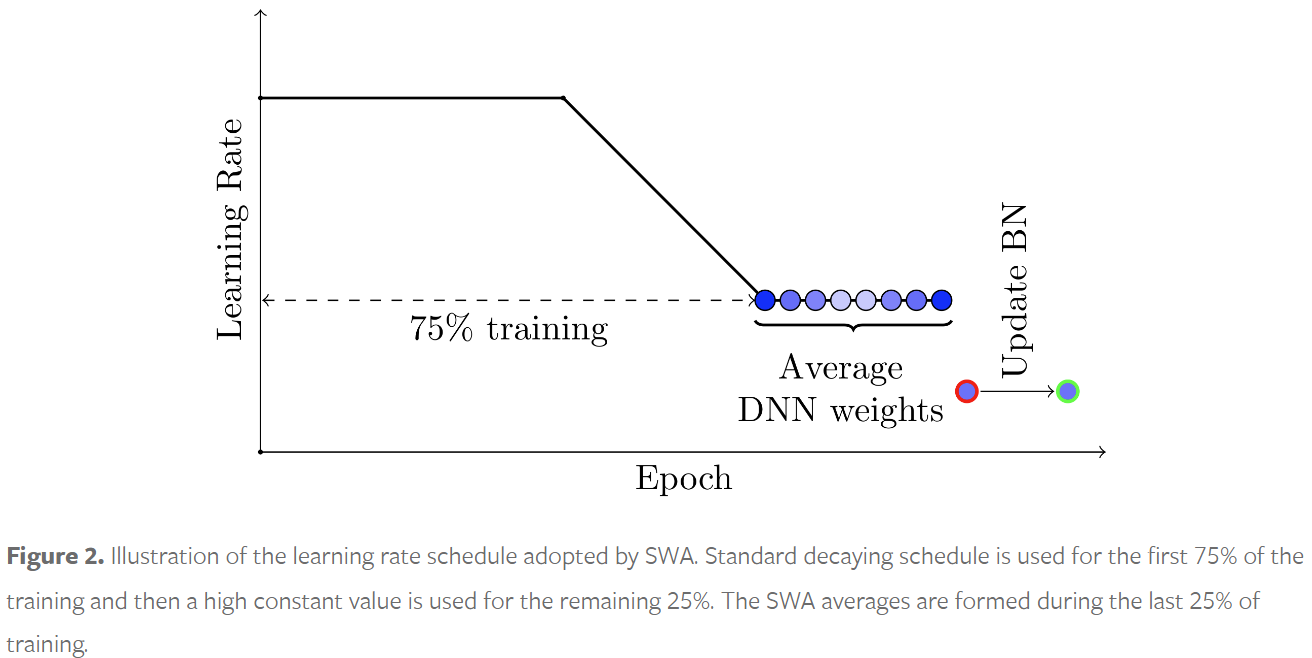
https://pytorch.org/blog/stochastic-weight-averaging-in-pytorch/

SGD에서 overfitting하거나 local minimum으로 수렴하는 것을 방지함으로써 model의 generalization을 향상시켜줍니다.

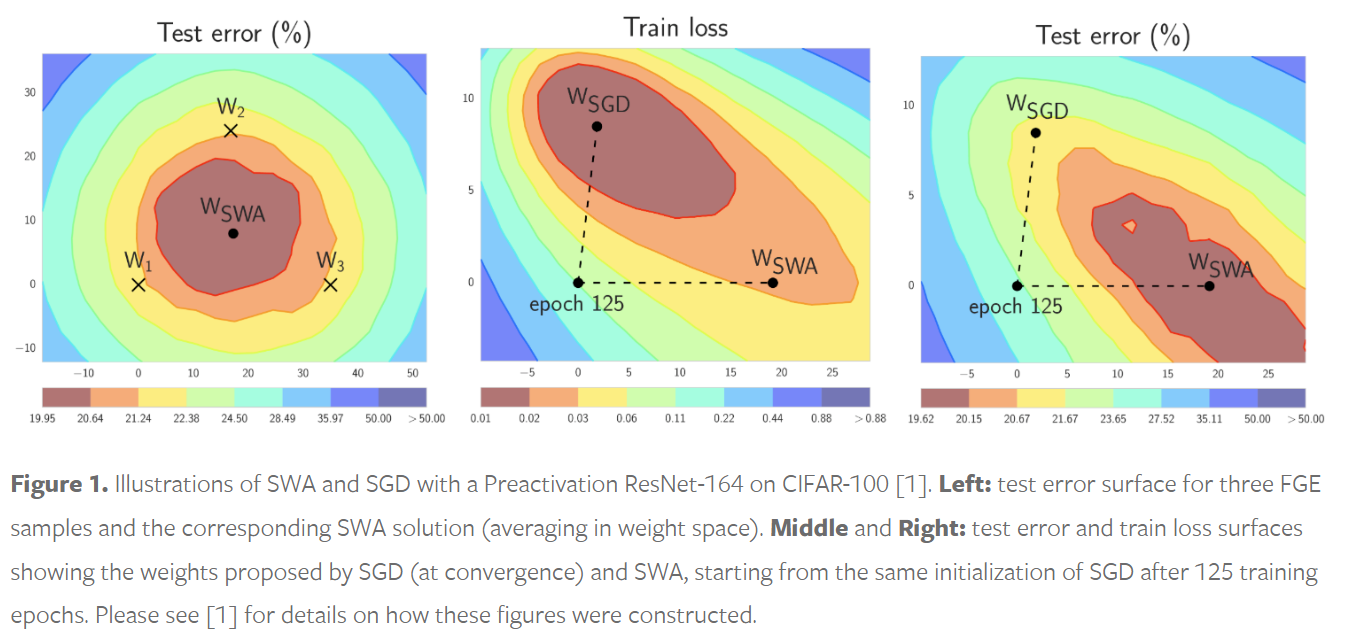
https://pytorch.org/blog/stochastic-weight-averaging-in-pytorch/

FedBE

앞서 살펴본 내용을 통합하여 FedBE 알고리즘을 정리해보겠습니다..

일단 model aggregation 이전, 즉 각 round마다 server가 global model를 sample된 client들에게 보내고, client를 그를 local data로 학습한 후, 그 결과인 local model $w_i$ 를 server에게 보내는 과정은 FedAvg와 동일합니다. 그 이후 server에 모인 local model들을 server가 aggregation하는 과정에 차이가 있습니다.

model aggregation을 위한 첫 단계로, 각 local model들을 하나의 가능한 global model (global model의 후보)로 여기고, 그들로 global model의 distribution을 구성합니다.

\[w^{(m)} \sim N(\mu, \Sigma) \\ where \quad \mu = \Sigma_i {\|D_i\| \over \|D\|} w_i, \quad \Sigma = \Sigma_i {\|D_i\| \over \|D\|}(w_i - \mu)^2\]

해당 distribution으로부터 $M$ 개의 model을 sampling 합니다. 이때 $w_i$ 들과 $\bar w$ 도 해당 distribution의 한 sample이라고 볼 수 있으므로 이들을 포함해 총 $M + N + 1$ 개의 model들로 Bayesian model ensemble을 수행하여 server의 nonlabeled data에 대한 pseudo-label을 추론합니다. server의 nonlabeled data에 이 pseudo-label을 붙혀 server의 dataset을 구성합니다.

\[p(y\|x, D) \approx {1 \over M} \Sigma_{m=1}^M p(y\|x, w^{(m)}), \ \ where \ \ w^{(m)} \sim p(w\|D)\]

생성된 server의 dataset을 사용하여 $\bar w$ 를 SWA 알고리즘으로 학습시킵니다. (Knowledge distillation) 그럼 학습된 model이 새로운 global model이 됩니다. 이 새로운 global model이 학습에 참여할 client들에게 전송되면서 새로운 round가 시작됩니다.

요약하자면 FedAvg의 aggregation 방식은 element-wise weighted averaging이고, FedBE의 aggregation 방식은 Bayesian model ensemble과 Knowledge distillation인 것입니다.

Experiment

dataset

총 50K개의 training data와 10K개의 test data로 이루어진 CIFAR-10, CIFAR-100과 200개의 class들에 대해서 각각 500개의 training data와 50개의 test data로 이루어진 Tiny-ImageNet을 사용했습니다. 간단하게 CIFAR-10에 대해서만 다루어보겠습니다.

setup

CIFAR-10의 training data 중 10K개를 server의 unlabeled data로 사용했고, 나머지 40K개의 training data를 10명의 client에게 나누어 할당했습니다. 이때 나누는 방법을 2가지 사용했는데 Step 방식과 Dirichlet 방식이 그것들입니다.

Step

각 client가 8개의 minor class와 2개의 major class를 가짐
각 minor class에 대해서 10개의 data가 할당됨
각 major class에 대해서 1960개의 data가 할당됨

Dirichlet

$\alpha = 0.1$인 디리클레 분포에 따라 training data를 할당함
각 client에게 할당된 data의 수가 다름

baselines

FedAvg
1-Ensemble
- 오직 한번의 round만 수행
FedBE
v-Distillation
- global model distribution에서 $M$개의 model들을 sampling하지 않고, 오직 local model $w_i$들만 사용
FedBE (w/o SWA)
- SWA를 사용하지 않고 knowledge distillation을 수행한 FedBE

results

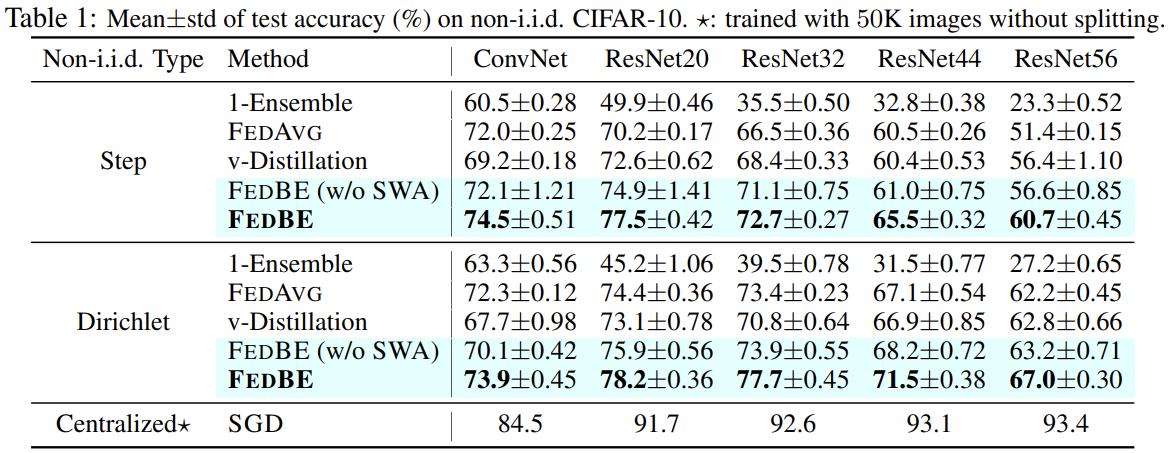
Table 1의 결과를 보면 모든 경우에서 FedBE의 성능이 다른 baseline들보다 높은 것을 확인할 수 있습니다. 또한 모델이 커질수록 성능 향상 폭이 커지는 경향성을 보입니다.

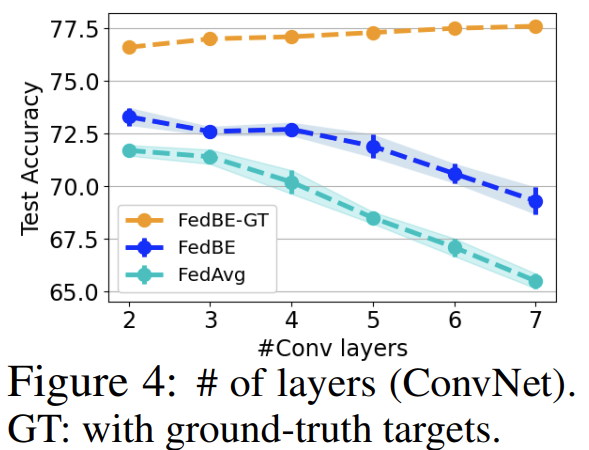
실제로 network에 layer를 추가하면서 실험해본 결과 (Figure 4), FedBE가 FedAvg에 비해서 성능이 하락하는 속도가 느렸습니다. network가 깊어질수록 성능이 나빠지는 이유는 local model이 client의 non-iid data에 over-fitting되었거나, 각 local model들이 학습되면서 서로 멀어졌기 때문입니다. 여기서 FedBE-GT는 knowledge distillation 과정에서 Bayesian ensemble (pseudo label을 쓰는 것)이 아닌 실제 ground truth label을 사용한 경우입니다. 실제 FL 환경에서는 불가능한 상황이지만, 각 local model들이 멀어지는 현상으로 server에서 방지해줌으로써 성능이 상당히 향상될 수 있음을 보이며, 또한 FedBE의 Baysian ensemble에서 noisy한 pseudo label을 어떻게 distill하는가가 FedBE의 성능에 큰 영향을 미친다는 것을 알 수 있습니다.

Conclusion

FL 환경에서 user들이 non-iid data를 가지고 있는 경우, local model들을 하나의 global model로 aggregate 하는 과정에서 어려움이 존재합니다. user들이 iid data를 가지고 있다면 local model들이 유사하게 학습되겠지만, non-iid data를 가지고 있다면 local model들의 parameter가 서로 다르게 학습될 가능성이 높기 때문에 단순한 방식으로 aggregation한다면 local model들의 성능을 유지하기 어렵습니다.

본 논문에서는, robust한 aggregation을 위해 Baysian inference를 도입해서 global model들을 sampling하고, 그들의 Bayesian Ensemble의 prediction rule을 Knowledge distillation을 통해 하나의 model에 전달하는 새로운 aggregation 알고리즘인 FedBE를 제안하였습니다.

FL에 있어서 server에서 local model들을 aggregation하는 과정은 불가피하기에, FedBE에서 제안한 방법 말고도 다른 aggregation 방법들을 찾아보시는 것도 추천드립니다. 또한 불확실성이 많은 DL에서 robustness를 확보하기 위해 Bayesian Ensemble을 적용할 수 있는 분야가 많을 것으로 기대됩니다.