TAMREF's profile image

TAMREF

April 22, 2023 00:00

Introduction

Single-Source Shortest Path (SSSP) 문제는 알고리즘 입문에서부터 다루는 아주 기초적이고, 또 중요한 문제입니다. 엄밀하게 적자면, $n$개의 정점과 $m$개의 가중치 있는 단방향 간선을 갖는 그래프 $G$와 시작 정점 $s$가 주어질 때, 모든 점 $i$에 대해 $s$에서 $i$로 가는 최단 경로의 길이 $\mathrm{dist}(s, i)$ 를 묻는 문제입니다.

일반적으로 가중치가 모두 양수인 경우에 사용할 수 있는 Dijkstra’s algorithm과 가중치의 값과 무관하게 사용할 수 있는 Bellman-Ford algorithm이 가장 유명합니다. 각각의 시간 복잡도는

• $\mathcal{T}[\text{Dijkstra}]$:
  • Practical한 선에서 $O(m \log n).$ (Johnson 1977)
  • Fibonacci Heap 등을 사용하면, $O(m + n \log n).$ (Tarjan 1987)
  • 정수 가중치를 가정하는 경우 $O(m + n \log \log n).$ (Thorup 2004)
• $\mathcal{T}[\text{Bellman-Ford}]$:
  • $O(mn)$ 시간에 shortest path를 찾거나, negative cycle을 반환. (Bellman 1958)

정도로 요약할 수 있습니다. 특히 negative weight가 있는 경우에는 total weight이 음수인 사이클이 존재하여 모든 점의 $\mathrm{dist}(s, i) = -\infty$가 되는 결과가 생길 수 있기 때문에, 음수 사이클을 detect하거나 (존재 여부 판별) 실제로 찾는 것이 또 하나의 중요한 문제가 됩니다.

일반적으로 Dijkstra-style의 shortest path는 복잡도가 사실상 optimum에 도달했기에 흥미로운 주제가 아니지만, Bellman-Ford의 경우 1958년의 결과 이후로 fully general improvement는 나오지 않은 상태입니다. 다만, 모든 가중치가 정수라는 꽤 합리적인 조건 아래서는 “Scaling Technique”이라는 종류의 기법이 발달하기 시작하며 유의미한 진보를 만들어내기 시작했습니다.

가중치의 절댓값이 $W$ 이하일 때,

• $O(m n^{3/4}\log W)$ (Gabow 1985)
• $O(m \sqrt{n} \log W)$ (Goldberg 1995)

시간 알고리즘이 개발되었습니다. 이렇듯 $\log W$ 에 대해 연산 이외에도 explicit한 다항식 시간 복잡도를 갖는 알고리즘을 weakly polynomial 알고리즘이라고 합니다. 여기까지는 (BNW 2022의 표현에 따르면) combinatorial algorithm의 면모를 잃지 않았습니다.

하지만 이후 SSSP보다 일반적으로 더 어려운 문제인 Min-Cost Flow가 2013년부터 급물살을 타며, 덩달아 SSSP의 복잡도도 개선되는 일이 일어났습니다. 가장 최신 버전에서는

• $\widetilde{O}((m + n^{1.5})\log W)$ (BLNPSSSW 2020)
• $O(m^{4/3 + o(1)})$ (AMV 2020)
• $O(m^{1 + o(1)})$ (CKLPPGS 2022 - Almost Linear Time Min-Cost Flow)

정도까지 시간복잡도가 개선되었습니다. 허나 최근 1년 사이에 combinatorial algorithm도 비약적으로 발전하였는데요, 첫 poly-logarithmic randomized algorithm이 2022년에 개발되었습니다.

• $O(m \log^{8} n \log W^{-})$ (Bernstein et al, 2022)
  • 여기서 $W^{-}$는 가장 절댓값이 큰 음수 가중치를 의미합니다.

Combinatoriality에 대해서는 명확하게 정의된 바가 없지만, 확실한 것은 이 알고리즘에 대한 코드까지 존재할 정도로 알고리즘의 명료함이 눈에 띈다는 것입니다. 하지만 1년 뒤, 그보다 더 간단한 subroutine으로 구성된 훨씬 낮은 복잡도의 (로그 개수가 적은) 알고리즘이 등장하여 주목을 받고 있습니다. 자칭 “log-shaving”의 결과물은 PS에서도 볼 수 있을 정도의 시간복잡도입니다.

• $O(m \log^{2} n \log(nW^{-}) \log\log n )$ (Bringmann et al, 2023.04)

나온지 채 한달이 되지 않은 만큼 디테일에서 많은 검증이 필요하겠으나, 논문에서 차용하는 subroutine은 하나하나가 매우 기초적이어서 읽어봄직합니다. 오늘은 이 논문의 내용을 리뷰하며, 동시에 “randomized algorithm”이 부여하는 놀라울 정도의 자유도에 대해 알아봅니다.

High-Level Description

Min-Cut, Shortest-Path Problem, Bipartite Matching 등 여러 문제를 보면 유독 weight가 존재한다는 사실만으로 복잡도에 polynomial gap이 생기는 경우가 더러 있습니다. 이를 극복하기 위한 테크닉 중 하나가 scaling technique입니다. 모든 간선의 weight를 $c < 1$ 배 shrink 시킨 문제를 재귀적으로 해결하고, 다시 $1/c$를 곱한 near-optimal solution을 구한 뒤 생기는 오차를 보정하는 방식의 방법론을 아우르는 말인데, 이 논문에서도 이와 비슷한 방법을 사용합니다.

1. (Restricted SSSP) 먼저 base case라고 볼 수 있는 “Restricted graph”에 대해서 문제를 해결합니다. 이는 평균적으로 $O(\mathcal{T}[\text{Dijkstra}]\cdot \log^{2} n)$ 정도에 high probability로 수행할 수 있습니다. 이를 $\mathcal{T}[\text{Restricted SSSP}]$로 표기합시다.
2. (NegC-Free-SSSP) 여기에 scaling technique을 활용하여 음수 사이클이 없는 그래프에 대해 high probability로 shortest path tree를 반환하는 알고리즘을 만들 수 있습니다. 이 알고리즘의 expected running time은 $O(\mathcal{T}[\text{Restricted SSSP}] \cdot \log(nW))$ 정도입니다. 하지만 이 알고리즘은 음수 사이클이 있는 그래프에 대해서는 terminate하지 않습니다. 대신 일정 시간동안 iterate하다가 멈추는 방법으로, 음수 사이클이 없는 경우에 항상 답을 찾아주고, 아닌 경우 FAIL을 리턴하는 기능을 구현할 수는 있습니다.
3. (Find-NegC) 음수 사이클이 없음에도 불구하고 억울하게 FAIL한 경우를 복원하기 위해, 음수 사이클을 실제로 명확하게 Report하는 부분이 필요합니다. $O(\mathcal{T}[\text{Restricted SSSP}]\log(nW) + \mathcal{T}[\text{Threshold}])$ 시간에 high probability로 음수 사이클을 찾을 수 있습니다.
   • 이 때 Threshold란 모든 간선의 가중치에 $M$을 더해서 negative cycle이 없도록 할 수 있는 최소 정수 $M$을 말하는데, BNW22에서는 $\mathcal{T}[\text{Restricted SSSP}] \cdot \log n \cdot \log (nW)$ 시간에, log shaving에 좀 더 진심인 Bringmann23 에서는 $\mathcal{T}[\text{Restricted SSSP}] \cdot \log(nW)$ 시간에 해결합니다.

여기서 high probability란 실패 확률이 $n^{-k}$ 꼴로 decay하는 랜덤 알고리즘을 의미합니다. 이를 도식으로 나타내면 아래와 같습니다.

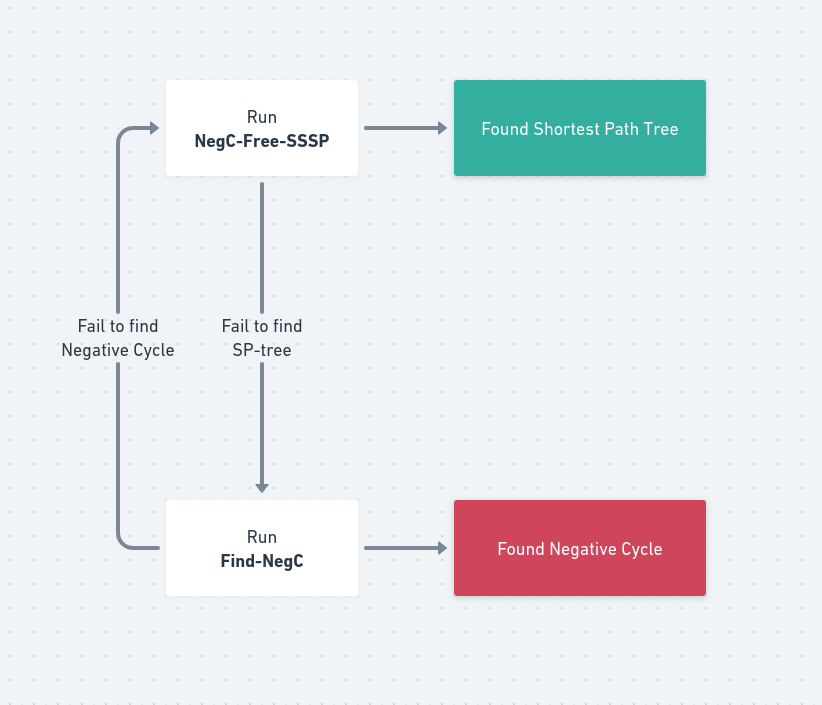
색칠된 상태는 모두 high probability로 도달할 수 있고, 계산한 shortest path tree와 negative cycle을 linear time에 검증할 수 있으므로 안전한 상태입니다. 각각이 만에 하나 실패하는 경우에도 왼쪽의 루프를 돌며 언젠가 (with high probability) 색칠된 두 상태 중 하나에 도달하게 되는 Las-Vegas Algorithm을 설계할 수 있습니다.

Base Case: Restricted Graphs

사실 위의 high-level architecture는 Bringmann에서 처음 제시한 것은 아니고, BNW22에서 처음 제시된 것이기는 합니다. 하지만 Bringmann23의 내용이 더 기초적이고, 결론도 더 강력하기 때문에 앞으로 BNW22의 context는 배제하고 설명하겠습니다.

Terms:

• $w(e)$: 간선 $e$의 가중치.
• $w(P)$: path/cycle/walk… 등이 될 수 있는 $P$에 대해 간선 가중치의 합
• $\overline{w}(C)$: cycle/closed-walk $C$에 대해 간선 가중치의 평균.

Definition of Restricted Graph

Restricted Graph란, 다음을 만족하는 그래프 $G$ (와 지정된 source $s$)를 말합니다.

• 모든 간선의 가중치는 $-1$ 이상.
• 모든 cycle의 평균 가중치는 $1$ 이상.
  • Formally, $\overline{w}(C) \ge 1$ for all cycle $C$.
• $s$에는 다른 모든 정점으로 가는 가중치 $0$의 간선이 있다.
  • 다시 말해, $\mathrm{dist} _ {G}(s, i) \le 0$.
  • 논문에서 따로 언급되진 않았으나, $s$에서 $i$로 가는 음수 간선은 없다고 가정해도 좋습니다. $s \to i$로 가는 가중치 $-1$의 간선이 존재할 경우 새로운 정점 $i^{\prime}$을 만들어 $s \to i^{\prime}$에 가중치 $0$, $i^{\prime} \to i$에 가중치 $-1$을 할당하면 최대 $2n$개의 정점을 가진 동일한 restricted graph를 만들 수 있기 때문입니다.

Decomposition of Restricted Graphs

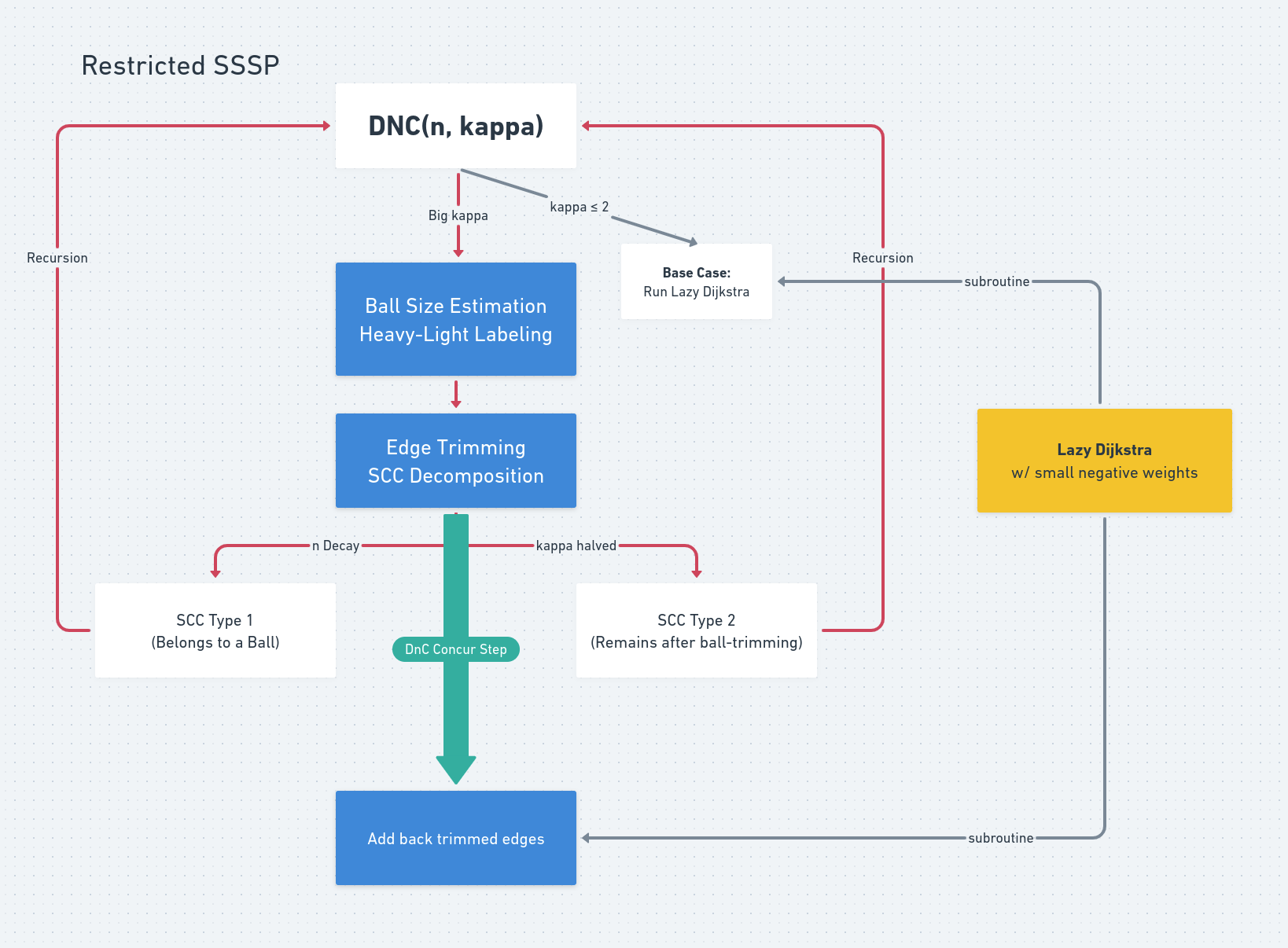
Restricted SSSP 문제를 해결하기 위해, 우선 가장 기본이 되는 building block인 Lazy Dijkstra 알고리즘에 대해 짚고 넘어가겠습니다.

Definition. (Relaxation count by negative edges)

$s$에서 $v$로 가는 shortest path 중 negative edge 개수의 최솟값을 $\eta _ {G}(v)$로 정의한다.

Definition. (Negative-abundance)

$\kappa(G)$를 $s$에서 출발하는 non-positive weight path $P$에 대해, negative edge의 개수의 최댓값으로 정의한다. 정의로부터, Restricted graph $G$에서는 모든 $v$에 대해 $\eta _ {G}(v) \le \kappa(G) \le n$임을 알 수 있다.

Algorithm. (Lazy-Dijkstra)

# Q := priority queue as normal dijkstra.

Q := PriorityQueue({dist: 0, vertex: s})
while Q is not empty:
    # run dijkstra using Q and non-negative edges only
    update_nonnegative_dijkstra(Q)

    # bellman-ford like relaxation for negative edges
    for (src, dst), weight in negative_edges:
        if dist[dst] < dist[src] + weight:
            dist[dst] = dist[src] + weight # relaxation
            Q.add({dist: dist[dst], vertex: dst}) # add relaxed vertex to Q

음수 사이클이 존재하지 않는 그래프에 대해, 다음의 알고리즘은 $O(\mathcal{T}[\text{Dijkstra}] \cdot \max _ {v} \eta _ {G}(v))$ 시간 안에 동작한다. 따라서 특히 Restricted graph의 경우 $O(\kappa(G) \cdot \mathcal{T}[\text{Dijkstra}])$ 시간에 동작한다.

직관적으로만 짚고 넘어가면, 가장 바깥의 while-loop을 $k$번째 돌았을 때 dist 배열은 Bellman-Ford 알고리즘의 성질에 따라 음수 간선을 최대 $k$개 사용하는 최단 경로를 나타내게 되고, 각 $v$에 대해 $\eta _ {G}(v)$번 loop이 지나면 더 이상 dist[v]가 갱신되지 않음을 알 수 있습니다.

우리의 전략은 다음과 같습니다.

1. 정점 개수 $n$, $\kappa(G)$의 overestimator $\kappa$ 를 key parameter로 들고 시작합니다. $\kappa \le 2$ 라면 LazyDijkstra를 이용하여 $\mathcal{T}[\text{Dijk}]$ 에 문제를 해결할 수 있습니다.
2. 앞의 두 과정 (Heavy-Light Labeling, Edge Trimming)을 거쳐 다음을 만족하는 간선의 집합 $L$을 찾아 제거합니다.
   • $G - L$의 남은 SCC들은 크기가 $3n/4$보다 작거나, $\kappa/2$보다 작은 negative abundance를 가진다.
   • $G$의 아무 shortest $s$-$v$ path $P$에 대해, $\mathbb{E}[\lvert P \cap L \rvert] = O(\log n)$. (Sparse hitting)
3. $G - L$의 SCC들에 대해 재귀적으로 Restricted SSSP를 풀어준 뒤, recursion에서 얻은 정보를 바탕으로 $L$ 이외의 간선들이 모두 non-negative인 equivalent graph $G _ {\phi}$ 로 변환합니다.
4. $L$ 이 더해진 그래프 $G$에서, $\mathbb{E}\lvert P \cap L \rvert \le O(\log n)$ 임을 이용하여 LazyDijkstra를 적용, $\mathrm{dist}(s, v)$를 계산합니다.

Equivalent graph 에 대해서 간단히 설명하고 바로 본론으로 들어갑시다.

Definition. (Equivalent Graph, Johnson’s trick)

Potential function $\phi : V(G) \to \mathbb{Z}$에 대해, 모든 간선 가중치를 $w _ {\phi}(u, v) := w(u, v) + \phi(u) - \phi(v)$로 바꾼 그래프는 기존과 equivalent하다고 하며, 특별히 $G _ {\phi}$로 표기한다.

두 equivalent graph에 대해, 어떤 경로가 한쪽에서 shortest path라면 나머지에서도 shortest path이다. 또한, equivalency에서 cycle weight는 불변이다.

위에 열거한 4개의 Step 중 Step 1, 4는 사실 더 코멘트할 것이 없습니다. Step 2와 Step 3을 주목합시다.

Step 2: Finding edges to be trimmed

보다 엄밀하게 말해, 우리는 다음을 만족하는 간선 집합 $L$을 찾아야 합니다.

• (DnC decay) $G - L$의 임의의 SCC $C$는 다음 조건 중 하나를 만족한다.
  • $\lvert C \rvert \le \dfrac{3n}{4}$.
  • $\kappa(C + \lbrace s \rbrace) \le \frac{\kappa}{2}$.
• (Sparse Hitting) 임의의 shortest path $P$에 대해, $\mathbb{E}\lvert P \cap L \rvert = O(\log n)$.

이를 위해 다음과 같이 “ball”들을 정의합니다.

• $\mathrm{OB} _ {G}(v, r)$: $\mathrm{dist}(v, x) \le r$인 정점들의 집합
• $\partial \mathrm{OB} _ {G}(v, r)$: $x \in \mathrm{OB} _ {G}(v, r), y \notin \mathrm{OB} _ {G}(v, r)$인 간선 $(x, y)$의 집합
• $\mathrm{IB} _ {G}(v, r)$: $\mathrm{dist}(x, v) \le r$ 정점들의 집합
• $\partial \mathrm{IB} _ {G}(v, r)$: $x \notin \mathrm{IB} _ {G}(v, r), y \in \mathrm{IB} _ {G}(v, r)$인 간선 $(x, y)$의 집합

음수 간선이 존재하는 경우에 Ball들은 connected가 아닐 수 있지만, ball을 생각할 때는 항상 간선 weight를 $\max(w(e), 0)$으로 바꾼 그래프 $G _ {\ge 0}$에서만 고려합니다.

편의상 $OB _ {G \ge 0}(v, r)$은 너무 기니 $\mathbf{O}(v, r)$, $\mathbf{I}(v, r)$ 등으로 줄여 쓰겠습니다.

Exploiting Decay Condition

이 때, $\min\left(\left\lvert\mathbf{O}(v, \dfrac{\kappa}{4})\right\rvert, \left\lvert\mathbf{I}(v, \dfrac{\kappa}{4})\right\rvert\right) \le \dfrac{3n}{4}$ 인 정점 $v$를 light하다고 할 때, 모든 light vertex $v$에 대해서

• $\left\lvert\mathbf{O}(v, \dfrac{\kappa}{4})\right\rvert \le \dfrac{3n}{4}$라면 $\partial \mathbf{O}(v, \dfrac{\kappa}{4})$ 를 모두 끊고,
• 그렇지 않다면 $\partial\mathbf{I}(v, \dfrac{\kappa}{4})$를 모두 끊어서

$\mathbf{O}(v, \dfrac{\kappa}{4})$ (또는 $\mathbf{I}(v, \dfrac{\kappa}{4})$)를 그래프에서 “파내고” 경계 간선들을 $L$에 포함시킨다면 DnC decay 조건을 만족할 수 있습니다. $L$을 제거하고 남은 SCC $C$들은 두 가지로 분류할 수 있는데,

Type 1. light vertex $v$의 $\mathbf{O}(v, \frac{\kappa}{4})$ $\mathbf{I}(v, \frac{\kappa}{4})$에 완전히 포함되는 경우. 이 때는 SCC의 크기가 정의에 따라 $\frac{3n}{4}$ 이하가 됩니다.

Type 2. 모든 light ball들을 파내고 남은 컴포넌트에 완전히 포함되는 경우. 이 때 $\kappa(C + \lbrace s \rbrace) \le \frac{\kappa}{2}$임을 증명하도록 합시다.

만약 가정이 거짓이라면, $C + \lbrace s \rbrace$에 음수 간선을 $\frac{\kappa}{2}$개보다 많이 포함하는 non-positive $s \to v$ path $P$가 존재할 것입니다. 이 때 $P$에서 첫 정점 $s$만을 빼내면 다른 정점 $u$에 대해 $u \to v$ path $P _ {1}$이 될텐데, $u, v$는 모두 light하지 않으니 $\mathbf{O}(v, \dfrac{\kappa}{4}), \mathbf{I}(u, \dfrac{\kappa}{4})$모두 $\frac{3n}{4}$보다 크게 됩니다. (사실은 $\frac{n}{2}$보다만 크면 되지만…) 때문에 둘의 교집합이 존재하고, 그말인즉슨 $G _ {\ge 0}$에 길이가 $\frac{\kappa}{2}$ 이하인 $v \to u$ path $P _ {2}$가 존재하고, $P _ {1}$과 $P _ {2}$를 이어붙여 만든 closed walk $Z$는 weight가 $w(P _ {1}) + w(P _ {2}) \le 0 + \frac{\kappa}{2} \le \frac{\kappa}{2}$이고, 음수인 간선만 $\frac{\kappa}{2}$보다 많으니 $\overline{w}(Z) < 1$이 됩니다. closed walk는 cycle들로 찢을 수 있으니, 이중에서 반드시 $\overline{w}(C) < 1$인 simple cycle을 찾을 수 있고 이는 Restricted Graph 조건에 모순이 됩니다.

이렇게 Decay 조건은 달성했는데, 앞으로 남은 것은 무엇일까요?

By-passing other conditions by randomness

가장 문제인 것은

• $\mathbf{O}(v, \frac{\kappa}{4}), \mathbf{I}(v, \frac{\kappa}{4})$ 의 크기를 모든 $v$에 대해서 알아내려면 $O(mn)$ 시간이 걸린다.
• 지금 전략으로는 Sparse Hitting Condition, 즉 $\mathbb{E}\lvert P \cap L \rvert$에 대한 어떠한 guarantee도 줄 수 없다.

의 두 가지 문제가 될 텐데, Bringmann23에서는 두 조건을 훌륭하게 randomness를 이용하여 우회합니다.

First bypass: random ball size estimation

(사실은 $\frac{n}{2}$보다만 크면 되지만…) 에서도 언급했듯이, 우리는 모든 ball size를 정확하게 estimate할 필요가 없고, ball의 크기가 $\frac{n}{2}$보다 큰지 / $\frac{3n}{4}$보다 작은지만 정확하게 판별하면 됩니다. 그 사이의 크기는 어떻게 분류되든 문제가 없기 때문입니다.

이를 다르게 해석하면 ball size를 $\frac{n}{8}$ 정도의 additive error로 추산할 수 있기만 하면 되는데, 이는 $O(mn)$보단 훨씬 빨리, high prob으로 수행할 수 있습니다.

Theorem. $O(\varepsilon^{-2} \log n \cdot \mathcal{T}[\text{Dijk}])$ 정도의 시간에, 주어진 $r$과 모든 $v$에 대해 $\mathbf{O}(v, r)$의 크기를 $\varepsilon n$ 정도의 additive error로 estimate할 수 있다.

Proof. $k := 5\varepsilon^{-2} \log n$ 개 정도의 정점 $u _ {1}, \cdots, u _ {k}$를 랜덤으로 샘플링하여 (중복 허용) $\mathbf{I}(u _ {j}, r)$을 계산합시다. 모든 $v$에 대해서 $\lvert \mathbf{O}(v, r) \rvert$의 estimate $\widetilde{O}(v)$를

$\widetilde{O}(v) := \frac{n}{k} \cdot \sum _ {j = 1}^{k} \left[ v \in \mathbf{I}(u _ {j}, r) \right]$로 주면, 놀랍게도 높은 확률로 additive error가 bound됩니다.

각 정점 $v$ 입장에서, 정점 $u _ {i}$를 뽑았을 때 $\mathbf{O}(v, r)$에 있을 확률이 $p _ {v} := \mathbf{O}(v, r) / n$이니, 결국 $\tilde{O}(v)$는 $\mathrm{Ber}(p)$를 따르는 독립적인 확률변수 $X _ {1}, \cdots, X _ {k}$ 의 합 $X$ (에 $n/k$를 곱한것) 이 될 것입니다. Hoeffding’s bound를 이용하면,

\(\begin{aligned} \mathrm{Pr}[\lvert \widetilde{O}(v) - \lvert \mathbf{O}(v, r) \rvert\rvert > \varepsilon n ] &= \mathrm{Pr}[\lvert X - \mathbb{E}X \rvert > \varepsilon k]\\ &\le 2\exp(-2\varepsilon^{2} k) \le 2n^{-10}. \end{aligned}\) 모든 정점에 대해서 additive error가 하나라도 튈 확률은 union bound를 생각하면 $2n^{-9}$ 정도가 됩니다.

Second bypass: randomizing $r \le \frac{\kappa}{4}$

사실 우리가 $\mathbf{O}(v, \frac{\kappa}{4})$ 를 사용했지만, $\frac{\kappa}{4}$보다 작은 어떤 값을 사용해도 문제가 없습니다. 따라서 light vertex $v$의 $\mathbf{O}(v, \frac{\kappa}{4})$를 전부 파내는 대신, $r \sim \mathrm{Geom}(20\log n / \kappa)$ 을 골라서 $\mathbf{O}(v, r)$을 파내면 어떨까요?

Geometric distribution을 고른 이유는 차치하고, 일단 $r$이 $\frac{\kappa}{4}$보다 클 확률이 $\left(1 - \frac{20\log n}{\kappa}\right)^{\kappa/4} \le n^{-5}$이므로, 파내는 ball의 크기는 높은 확률로 $3n/4$ 미만일 것이 보장됩니다. 이제 어떤 shortest path $P$에 대해 $\mathbb{E}\lvert P \cap L \rvert$를 계산해 봅시다.

보다 원론적으로는 임의의 간선 $e = (x, y)$에 대해 $\mathrm{Pr}[e \in L]$을 생각할 수 있습니다. Exhaustive case analysis를 해보면

• $y \in \mathbf{O}(v, r)$인 경우, $y$는 함께 파내어지기 때문에 $e$도 제거되고, 더 이상 $L$에 들어갈 수 없습니다.
• $x, y \notin \mathbf{O}(v, r)$인 경우, $x, y$는 이 과정에서 변화가 없습니다. 대신 다른 $\mathbf{O}(v^{\ast}, r)$을 파낼 때 영향을 받을 수는 있습니다.
• $x \in \mathbf{O}(v, r), y \notin \mathbf{O}(v, r)$인 경우 $e \in \partial\mathbf{O}(v, r)$이므로 $L$에 들어갑니다.

따라서 마지막 case에 속할 확률만 생각해보면 $\displaystyle\max _ {v} \mathrm{Pr}\left[ r < \mathrm{dist}(v, y) \mid r \ge \mathrm{dist}(v, x) \right]$ 정도로 bound할 수 있습니다. sum 등의 bound를 사용하지 않는 이유는 한번 $e \in L$이 성립하면 다시 고려할 필요가 없기 때문입니다.

Geometric distribution의 memoryless property에 의해, 이 확률의 upper bound는 $\max _ {v} \Pr[r < \mathrm{dist}(v, y) - \mathrm{dist}(v, x)] = \Pr[r < \max _ {v}(\mathrm{dist}(v, y) - \mathrm{dist}(v, x))] \le \Pr[r < w _ {G _ {\ge 0}}(e)] = 20w _ {G \ge 0}(e)\log n / \kappa$가 됩니다.

따라서 $G$의 shortest path $P$ 에 대해 $\mathbb{E}\lvert P \cap L \rvert = \frac{20\log n }{\kappa} \cdot w _ {G \ge 0}(P)$ 로 쓸 수 있습니다. 이 때 $w(P) \le 0$이고, (모든 shortest path는 직접적으로 이어진 간선 0보단 작거나 같아야 하므로) 많아야 $\kappa$개의 음수 간선이 있으므로 양수 간선도 $\kappa$개 이하가 됩니다. $w _ {G \ge 0}(P) \le \kappa$가 성립하고, 따라서 $\mathbb{E}\lvert P \cap L \rvert = O(\log n)$이 됩니다.

이렇게 기나긴 Step 2가 끝났습니다. randomized algorithm의 힘을 실감할 수 있는 순간입니다.

Step 3. “Concur step” - equivalent transformation

$L$을 잘 빼낸 것 까지는 좋았는데, 이제 LazyDijkstra를 활용하여 $L$을 다시 잘 붙이려면 음수 간선은 오직 $L$에만 있도록 가중치 변환을 잘 해줘야 합니다. 그래야 LazyDijkstra의 시간 복잡도가 깨지지 않기 때문입니다.

자세한 증명은 BNW22의 Appendix에 나와 있으나, 직관적으로 받아들이기 어려운 내용은 아니니 간단히만 읊고 넘어가겠습니다. 목표는 결국 음수 간선을 모두 없애는 것인데, DNC에서 분리한 SCC내부의 음수 간선과 SCC들로 이루어진 DAG의 음수 간선을 모두 고려해야 합니다.

SCC $C \cup \lbrace s \rbrace$ 내부의 음수 간선들은, $\phi _ {1}(v) = \mathrm{dist} _ {C \cup \lbrace s \rbrace}(s, v)$ 로 두면 정리할 수 있습니다. 정의상 $L$의 간선들은 SCC내부에 존재할 수 없으니 여기서는 굳이 같이 update해주지 않아도 됩니다.

이제 $G _ {\phi _ 1}$의 SCC 내부 간선들은 모두 non-negative weight를 갖게 되었으니, DAG 간선을 정리해줍시다. DAG의 위상 정렬을 구한 뒤, 각 $v$에 대해 내가 속한 SCC의 rank $\mathrm{rk}(v)$를 정의하여 (source에 가까울수록 큰 rank를 가집니다) $\phi _ {2}(v) = \lvert -1 \rvert \mathrm{rk}(v)$ 로 주면 됩니다. 굳이 $\lvert -1 \rvert$를 강조하여 쓴 이유는 일반적인 그래프에서도 $\varphi(v) := \lvert W^{-} \rvert \mathrm{rk}(v)$의 potential을 주면 음수 간선을 제거할 수 있기 때문입니다.

여기서는 $L$의 간선들도 업데이트를 해줘야 합니다. $L$의 간선들은 위상 정렬 순서를 역행할 수도 있기 때문에, 음수 간선이 될 수도 있음에 유념합시다.

Conclusion

알고리즘의 expected running time을 계산해보면

• 재귀 깊이가 $\log(n \kappa)$입니다.
• 각 스텝에서,
  • ball size estimation에 $\log n$번의 dijkstra가 필요합니다.
  • ball을 파내는 데에는 (amortized manner로) 한 번의 dijkstra에 상당하는 시간이면 충분합니다.
  • SCC, 위상정렬, equivalent graph로의 변환은 선형 시간에 됩니다.
  • $L$의 간선들로 Lazy Dijkstra를 돌리기 위해 $\log n$번의 dijkstra가 필요합니다.

$\kappa$의 initial guess는 $n$으로 잡으면 충분하니, 결국 $O(\log^{2} n)$ 번의 다익스트라 알고리즘으로 Restricted SSSP 문제를 해결할 수 있습니다. Practical한 선의 복잡도는 $O(m \log^{3} n)$으로, BNW의 $O(m \log^{5} n)$에 비해서는 acceptable합니다. 논문이 주장하는 복잡도는 Thorup Priority Queue를 사용한 $O(m \log^{2} n \log \log n)$이나 논외로 합시다.

이 알고리즘은 Las-Vegas algorithm으로, randomness에 의한 failure가 일어나더라도 시간 복잡도가 증가할 뿐 틀리진 않습니다. 다만 전체 알고리즘의 시간 복잡도 보장을 위해 논문에서는 주어진 time budget안에 끝나지 않으면 terminate하는 방식으로 Monte-Carlo version을 사용합니다.

이미 글의 분량이 매우 길어져, 전체 문제를 해결하는 부분은 다음 달 글에서 이어 다루어야 할 듯합니다. 앞서 말했듯 전체 문제는 Restricted SSSP를 black-box subroutine으로 사용하는 일종의 Scaling algorithm입니다. 여기서도 여러 기발한 random art들이 많으니, 이 글을 관심있게 읽으셨다면 다음 달에 올라올 속편도 기대해 주시기 바랍니다.

더불어, 이 알고리즘의 구현체도 여유가 되는대로 작업해볼 예정입니다. 관심있으신 분께서는 연락 주시면 감사하겠습니다.

Reference

• Bringmann, Karl, Alejandro Cassis, and Nick Fischer. “Negative-Weight Single-Source Shortest Paths in Near-Linear Time: Now Faster!.” arXiv preprint arXiv:2304.05279 (2023).
  • 오늘의 메인 논문입니다.
• Bernstein, Aaron, Danupon Nanongkai, and Christian Wulff-Nilsen. “Negative-weight single-source shortest paths in near-linear time.” 2022 IEEE 63rd Annual Symposium on Foundations of Computer Science (FOCS). IEEE, 2022.
  • 기존의 SOTA 논문인 BNW22로, 권위 있는 저널인 FOCS에 출판되었습니다. Bringmann23이 제시하는 대부분의 high-level structure가 이 논문에서 기인했습니다. 물론 Bringmann23은 충분히 self-contained되어 있어서 모두 읽을 필요까지는 없습니다.
• Garbow, Harold N. “Scaling algorithms for network problems.” Journal of Computer and System Sciences 31.2 (1985): 148-168.
  • Scaling algorithm를 재조명한 Gabow의 논문입니다.
• Goldberg, Andrew V. “Scaling algorithms for the shortest paths problem.” SIAM Journal on Computing 24.3 (1995): 494-504.
  • SSSP를 $m\sqrt{n} \log W$ 시간에 해결한, combinatorial algorithm 분야에서 최근 수십년간 SOTA를 차지하고 있던 논문입니다. Detrministic으로 한정하면 아직 이 논문을 뛰어넘은 결과는 없으니, 이 글의 중간 중간 나온 random trick이 영 미덥지 않은 분들께 일독을 권합니다.