TAMREF's profile image

TAMREF

May 21, 2023 00:00

Introduction

지난 글에 이어 Bringmann 2023의 near-linear time shortest single source path (SSSP) 문제를 해결하는 부분을 더 다루어보도록 하겠습니다. 간선의 가중치가 $-W^{-}$ 이상인 weighted digraph에 대해 $\mathcal{O}(\log^{2} n \log(nW))$ 번의 dijkstra algorithm으로 shortest path tree, negative cycle 중 하나를 반환하는 문제입니다.

지난 글에서는 다음의 특수한 조건을 만족하는 Restricted SSSP (RSSSP)를 $\mathcal{O}(\log^{2} n)$ 번의 dijkstra algorithm으로 해결하는 Las-Vegas algorithm을 소개하였습니다.

Definition. Directed graph $G$에 어떤 정점 $s \in V(G)$가 존재하여 다음을 만족하면 $G$를 restricted graph라고 한다.

• 모든 간선의 weight는 $-1$ 이상의 정수.
• 모든 cycle은 average weight가 $1$ 이상.
• $s$에서는 다른 모든 정점으로 가는 가중치 $0$의 간선이 존재한다.

이번에는 $\mathcal{O}(\log(nW))$번의 RSSSP subroutine으로 전체 문제를 해결하는 방법을 소개하도록 하겠습니다. unweighted graph problem을 weighted graph problem으로 변환하는 일련의 테크닉을 scaling method라고 부르는데, 그 정수를 맛볼 수 있습니다.

Graphs without negative cycle

그 첫 번째로 음수 사이클이 없는 그래프의 SSSP를 해결하여 보겠습니다. 큰 plot을 보면 아래와 같습니다.

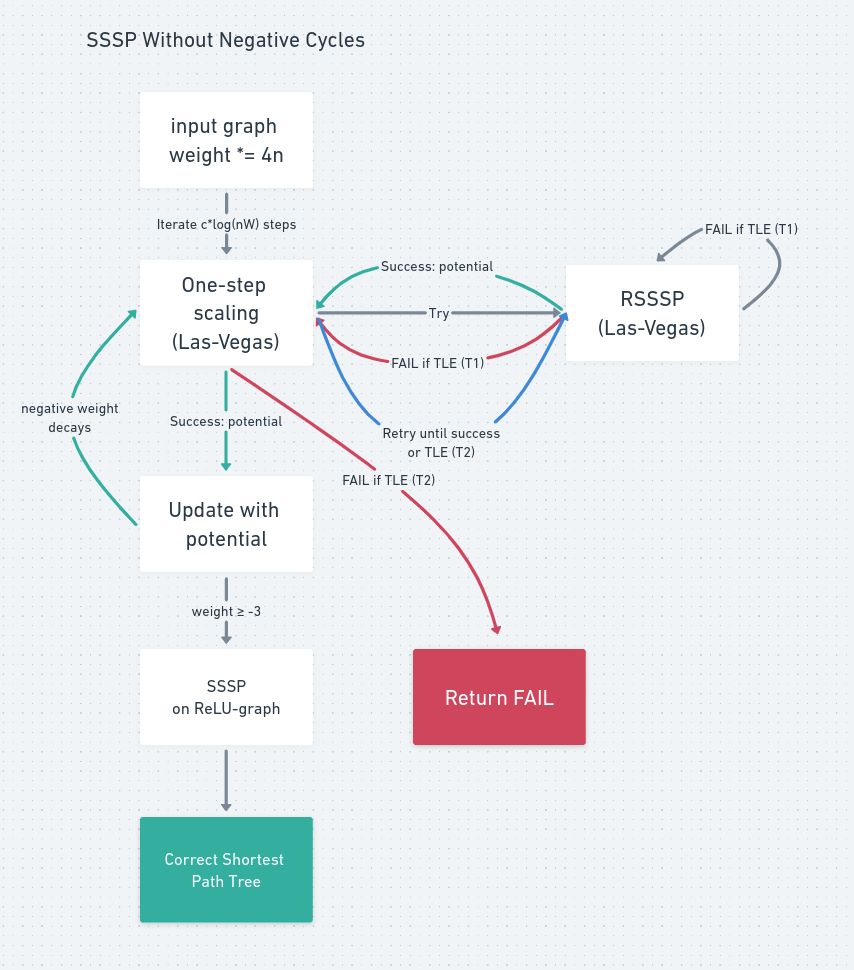
가장 핵심이 되는 것은 One-step scaling이라는 subroutine으로, $\mathcal{O}(\log(nW))$번 반복됩니다.

기본적으로 어떤 restricted graph를 만들어 RSSSP subroutine을 계속 호출하되, 정해진 time budget $T _ {1}$ 안에 종료되지 않으면 FAIL하는 Monte-Carlo 버전을 사용합니다. $T _ {1}$은 RSSSP의 expected time complexity인 $\mathcal{O}(\log^{2} n)$번의 다익스트라를 돌리기에 충분한 시간으로 설정합니다\dots

만약 성공하는 경우 RSSSP는 어떤 potential $\phi$를 반환하고, $G$를 $G _ {\phi}$로 변환하면 negative weight이 $2/3$배로 줄어들게 됩니다. 만약 전체 시간이 $T _ {2}$를 넘어서면 실패 (즉, 그래프에 음수 사이클이 존재할 것)로 판단하고 FAIL을 반환합니다. $G _ {\phi}$의 정의에 대해서는 지난 글을 참고하세요.

FAIL하지 않았다면 $\mathcal{O}(\log(nW))$번의 one-step scaling이 모두 종료되고, weight가 $-3$ 이상인 그래프가 반환됩니다. 여기서 negative weight는 전부 $0$으로 간주하고 Shortest Path Tree를 구하면 원래의 그래프에서도 올바른 SP-Tree임이 보장됩니다.

1. One-step Scaling

Theorem. $W \ge 1$에 대해 모든 간선의 가중치가 $-3W$보다 큰 negative-cycle free graph $G$를 생각하자. 이 때 한 번의 RSSSP subroutine으로 $G _ {\phi}$의 가중치가 $-2W$보다 크게 되는 potential $\phi$를 얻을 수 있다.

물론 전체 문제를 해결하기 위해서는 RSSSP가 주어진 시간 안에 성공하지 못하는 경우, $G$에 negative cycle이 들어오는 경우 등을 생각해줘야 하지만 여기서는 이상적인 케이스만 먼저 보겠습니다.

Proof. 간선 $e \in E(G)$에 대해, $w _ {H}(e) = \lceil \frac{w _ {G}(e)}{W} \rceil + 1$으로 정의된 그래프 $H$를 생각하고, 여기에 artificial source $s$를 추가해서 다른 모든 정점으로 가는 가중치 $0$의 간선을 추가합시다.

• $w _ {G}(e) > -3W$이므로 $w _ {H}(e) \ge -1$이 보장됩니다.
• $H$의 cycle $C$는 $s$를 포함할 수 없으므로 원래 그래프인 $G$에도 포함됩니다. average weight $\overline{w} _ {H}(C) \ge 1 + \frac{1}{\lvert C \rvert} \sum _ {e \in C} \frac{w _ {G}(e)}{W} = 1 + \frac{\overline{w} _ {G}(C)}{W} \ge 1$이 성립합니다.

따라서 $H$는 restricted graph가 되고, RSSSP를 실행하여 $s$에서 가는 shortest path tree $T$를 얻을 수 있습니다. 이 때 $\phi(v) := W \cdot \mathrm{dist} _ {T}(s, v)$를 생각하면, $G _ {\phi}$의 각 간선은

\[\begin{aligned}w _ {G _ {\phi}}(u, v) &= w _ {G}(u, v) + \phi(u) - \phi(v)\\ &= w _ {G}(u, v)- W(\mathrm{dist} _ {T}(s, v) - \mathrm{dist} _ {T}(s, u))\\ &= w _ {G}(u, v) - W\cdot w _ {H}(u, v)\end{aligned}\]

를 만족하게 됩니다. 이 때 $w _ {H}(e) < \frac{w _ {G}(e)}{W} + 2$에서 $w _ {G}(e) - w _ {H}(e) > -2W$를 만족하므로 Theorem의 조건을 만족합니다. $\square$

Notes

여기서 $G$에 음수 사이클이 있는 경우, One-step scaling에서 만들어진 $H$자체가 restricted graph가 아니게 됩니다. Restricted graph가 아닌 경우에 RSSSP를 돌리게 되면, 지난 글에서 다뤘듯 light ball들을 전부 파내고 난 뒤의 컴포넌트의 $\kappa$가 충분히 작아지지 않을 수 있고, TLE로 이어질 수 있습니다. 그 이외의 부작용은 우려하지 않아도 됩니다. $H$에 음수 사이클이 있다면 Shortest Path Tree부터가 제대로 return되지 않을 것이고, $G$에 음수 사이클이 있다면 $G _ {\phi}$에도 있으니, 마지막에 Shortest Path Tree를 리턴하기 직전의 validation에서 실패하게 되기 때문입니다.

2. SSSP on ReLU graph

ReLU graph란 이름처럼 간선의 negative weight를 $0$으로 대체한 그래프입니다. 여기서는 어렵지 않게 dijkstra’s algorithm을 적용할 수 있긴 한데, 왜 이렇게 할 수 있을까요?

이는 flow-chart의 맨 처음에 위치한, 가중치에 $4n$배를 해주는 이유와 관련이 있습니다. 이 순간 negative weight가 $4nW^{-}$가 되기 때문에 one-step scaling을 반드시 $\mathcal{O}(\log(nW^{-}))$번 돌려야 할 필요성이 생기는데요, 이런 비용을 감수하는 이유가 다 있습니다.

One-step scaling이 모두 끝난 그래프 $G _ {\psi}$를 생각합시다. 이는 원래 초기의 scaled graph $G$와 비교해 어떤 potential $\psi$를 적용한 상태일 것입니다. 따라서 임의의 두 $uv$-path $P _ {1}, P _ {2}$에 대해 $w(P _ {1}) - w(P _ {2})$는 $G$와 $G _ {\psi}$에서 동일할 것입니다.

따라서 어떤 non-shortest $uv$-path $P$ of $G _ {\psi}$에 대해 $w _ {G _ {\psi}}(P)$는 $\mathrm{dist} _ {G _ {\psi}}(u, v) + 4n$이상이 됩니다. 이 때 $\mathrm{dist} _ {\mathrm{ReLU}(G _ {\psi})}(u, v) \le \mathrm{dist} _ {G _ {\psi}}(u, v) + 3(n-1)$이 성립함에 주목합시다. $G _ {\psi}$의 간선은 가중치가 $-3$보다 크고, 최대 $n-1$개의 간선을 이용할테니까요. 따라서 $P$는 $\mathrm{ReLU}(G _ {\psi})$에서도 shortest path가 될 수 없고, $\mathrm{ReLU}(G _ {\psi})$의 shortest path만 찾아줘도 충분합니다.

Finding a negative cycle

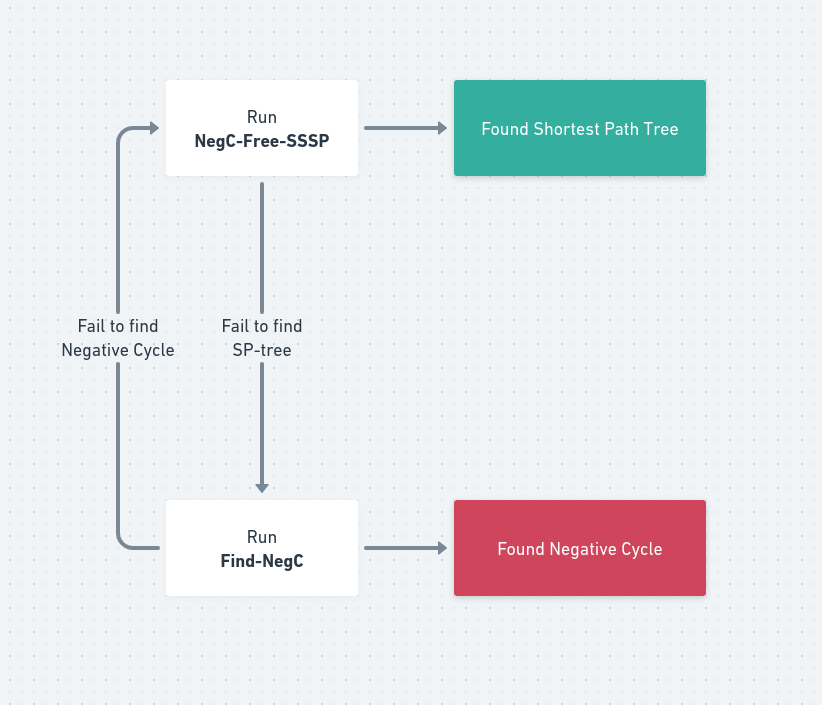
지난 글에서도 보았듯, 전체 알고리즘이 완전히 동작하기 위해서는 음수 사이클이 존재할 때 report하는 알고리즘도 존재해야 합니다. 첫 번째 조각인 negative cycle-free case의 SSSP는 증명을 마쳤으니 이제 동일한 시간복잡도에 negative cycle을 찾아주는 알고리즘을 찾아봅시다.

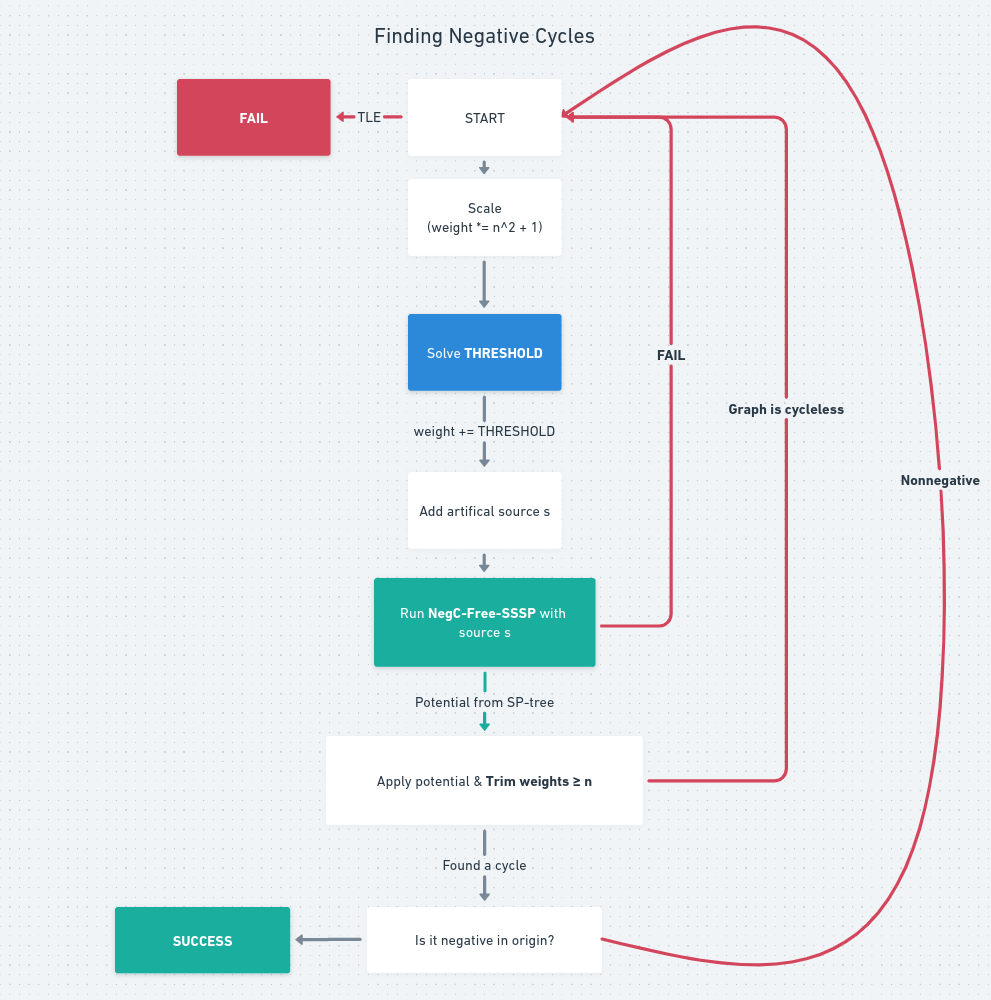
여기서 사용하는 subroutine은 처음 보는 THRESHOLD와, 이미 뭔지 아는 Negative Cycle Free SSSP로 이루어져 있습니다. 나머지는 모두 linear time에 동작하니 시간복잡도는 이 두 term에 의해 결정됩니다. NegC-Free-SSSP는 $\mathcal{O}(\log^{2} n \log(nW))$ dijkstra로 알고 있으니 THRESHOLD라는 놈이 뭔지, 몇 번의 dijkstra로 해결할 수 있는지가 중요할 것입니다.

사실 모든 weight에 어떤 값을 더한다는 점, 더한 뒤에 NegC-Free-SSSP를 돌린다는 점에서 짐작할 수 있듯 THRESHOLD는, 간선의 모든 weight에 uniform constant $M$을 더했을 때 그래프가 negative-cycle free가 되는 최소의 자연수 $M$을 찾는 문제입니다. 어떻게 보면 minimum cycle weight의 floor를 구하는 문제로 볼 수 있겠습니다.

아니 그렇다면, 왜 다음의 알고리즘을 쓰지 않는 건가요?

• $M = \mathrm{Threshold}(G)$를 구한다.
• $M > 0$이면 100% confidence로 negative cycle을 구한다.
• $M = 0$이면 100% confidence로 SP-tree를 구한다.

아쉽게도 THRESHOLD자체가 NegC-Free-SSSP를 subroutine으로 갖는 randomized algorithm이기 때문에 그렇습니다. 이 자체를 $\mathcal{O}(\log^{2} n \log(nW))$ dijkstra만으로 돌리기 위해서도 상당한 지면이 할애됩니다.

High-level correctness

더 세부적으로 파고 들기 전에, 전체 그림에도 수상쩍은 숫자들이 많으니 알고리즘의 correctness부터 구해봅시다.

Proposition 1. Input graph $G$가 negative cycle을 갖는다고 하고, THRESHOLD의 return value를 $M$이라고 하자. $M > n^{2}$이 성립한다.

Proof. Negative weight cycle이 존재하고, 이 때 cycle average weight의 최댓값은 $-\frac{1}{n}$일 것이다. 하지만 $n^{2}+ 1$배 scale한 것의 영향으로 $-\frac{n^{2}+1}{n} < -n$ weight의 cycle이 존재하고, 따라서 항상 $M > n$.

Proposition 2. $G$의 minimum (negative) weight cycle $C$는 마지막 step (After Trimming edges with weight $\ge n$)에서도 항상 cycle이 된다.

Proof. 편의상 모든 과정 (Threshold, SSSP로 얻은 potential applying, weight $\ge n$이상인 간선 쳐내기) 을 마쳐서 얻은 그래프를 $H$라고 하자. 이 때 cycle $C$의 weight에 영향을 주는 것은 threshold adding뿐이고, 이로 인해서 얻어진 average weight는 $1$ 미만임이 보장된다. 따라서 모든 간선의 weight를 다 합해도 $\lvert C \rvert \le n$ 미만임이 보장되고, potential의 영향으로 모든 간선의 가중치가 $0$ 이상이므로 각 간선의 가중치가 $n$ 미만임 또한 보장된다.

Proposition 3. $H$의 cycle은 항상 $G$의 negative weight cycle이 된다.

Proof. cycle의 average weight가 $n-1$ 이하이므로, $G$에서 이 cycle의 weight는 $(n-1-M)\lvert C \rvert < 0$이 된다. $\square$

따라서 $G$에 negative cycle이 있고 구한 $M$이 정확하다면 전체 알고리즘이 정확하다는 것을 보장할 수 있습니다.

Slow method for THRESHOLD

사실 Threshold를 구하는 Monte-Carlo algorithm은 아주 쉽게 만들 수 있습니다. $M$에 대한 binary search를 하면 되죠. 모든 간선에 $M$을 더해보고, 그래프에 negative cycle이 없다면 더 작은 $M$을, 있다면 더 큰 $M$을 시도해보면 됩니다.

하지만 negative cycle oracle이 그렇게 쉽게 될 리가요. 다음과 같은 확률적인 oracle을 사용합니다.

Theorem. One-step scaling을 $k$번 반복하는 알고리즘을 생각하자. 다음이 보장된다. 가중치가 $-W$이상인 그래프 $G$에 대해서, ($W \ge 24$)

• 그래프에 음수 사이클이 없다면 $1 - \exp(-k)$ 이상의 확률로. $G _ {\phi}$의 가중치가 $-\frac{3}{4}W$ 이상이 되는 potential $\phi$를 반환한다.
• 그렇지 않은 경우 NegCycle을 반환한다.

Proof. $G$에 negative cycle이 없는 경우만 생각하면 됩니다. One-step scaling이 한 번이라도 성공한다면 $-2\lceil W / 3 \rceil$ 이상의 가중치를 갖는 그래프를 얻을 수 있으니, $W \ge 24$임을 감안하면 충분합니다. 각 시행을 constant probability로 성공하는 독립시행으로 생각할 수 있으니, 기하분포를 이용하면 확률 bound도 증명할 수 있습니다.

앞으로 이 시행을 Testscale(G, k)라고 부르겠습니다.

이를 바탕으로 $\mathcal{O}(\log n \log(nW))$번의 RSSSP로 문제를 해결할 수 있습니다. $k = 10\log n$ 정도로 잡으면 failure probability가 $n^{-10}$ 정도로 나올테니, $\log(nW)$번 정도의 binary search에서 한 번이라도 실패할 확률이 매우 낮게 됩니다.

구체적인 실행 과정을 요약하면, 그래프의 minimum weight를 $\omega$라고 할 때

• $\omega \le 48$이면 그냥 $t = 0, \cdots, \omega$에 대해 모든 간선에 weight $t$를 더한 그래프 $G^{+t}$에 대해 $\mathrm{Testscale}(G^{+t}, 10\log n)$을 실행하면 됩니다.
• 그렇지 않은 경우 $M = \omega / 2$로 두고, $\mathrm{Testscale}(G^{+M}, 10\log n)$의 결과에 따라 binary search의 다음 step으로 이동합니다. 물론 $\omega$가 줄어들어야 하니, $\mathrm{Testscale}$의 반환값이 어떤 potential $\phi$라면 $G$를 $G _ {\phi}$로 바꿔주어야 이분탐색이 말이 됩니다.

시간 복잡도는 초기 $\omega = nW$이니 $\log n \log (nW)$ 번의 RSSSP를 실행하는 시간 복잡도와 같게 됩니다. 하지만 우리는 $\mathcal{O}(\log(nW))$ 번 정도의 RSSSP만 사용해야 우리가 원하는 시간 복잡도를 달성할 수 있는데요, 특수한 binary search 기법으로 이를 달성해보겠습니다.

Fast THRESHOLD algorithm

우선 매번 Testscale에서 $\mathcal{O}(\log n)$번의 RSSSP를 사용하는 것이 굉장한 낭비가 되고 있으니, 이걸 줄일 방법을 고안해봅시다.

아이디어는 Negative weight $W$와 $M = \mathrm{Threshold}(G)$에 대해, potential을 계속 업데이트해가며 $W - M$을 줄여가는 것입니다. $M$이 minimum cycle weight임을 생각하면, 직관적으로 potential을 잘 주면 $W = M$이 되도록 만들 수 있겠다는 생각이 듭니다.

어떤 “stride parameter” $\Delta$를 선정해서 $\mathrm{TestScale}(G^{+(W - \Delta)}, k)$ 가

• $\phi$ 를 반환하는 경우, $W - \Delta \ge M$이므로 $\Delta$를 2배로 키우고, $G$를 $G _ {\phi}$로 변환하여 $W$ 자체를 감소시킵시다.
• NegCycle 을 반환하는 경우, (아마도) $W - \Delta < M$이므로 $\Delta$를 절반으로 줄입니다. ($\Delta \gets \lceil \Delta / 2 \rceil$)

이를 적당히 $\Theta(\log(nW))$ 번 반복한다면 그래프 $G$의 negative weight $W _ {\mathrm{final}}$이 높은 확률로 $M$이 될 것입니다. 언뜻 여기까지는 느린 방법에 비해 개선점이 없는 것 같지만, 중요한 것은 $k = \log(100)$ 정도의 상수로 둬도 충분하다는 사실입니다. 편의상 위 과정을 $\mathrm{Step}(k)$라고 부릅시다.

Objective metric

$\mathrm{Step}(k)$를 $t$번 시행한 후의 그래프를 $G _ {t}$, negative weight를 $W _ {t}$, stride를 $\Delta _ {t}$라고 둡시다. 특별히 $\Delta _ {0} := 2$입니다. 이 때 objective를

\[D _ {t} := (W _ {t} - M)^{20} \cdot f(\frac{W _ {t} - M}{2\Delta _ {t}})\]

where $f(x) := \max(x, \frac{1}{x})$로 정의하면, 놀랍게도 다음이 성립합니다.

Theorem (Multiplicative Drift). $\mathrm{Step}$의 parameter $k = \lceil \log(100) \rceil$ 이라고 하자. 다음이 성립한다. $\mathbb{E}[D _ {t+1}] \le 0.7D _ {t}$

Proof. 잠시 뒤에.

Theorem (Decay of Multiplicative Drift) Non-negative Random variable sequence $X _ {1}, X _ {2}, \cdots$에 대해 $\mathbb{E}[X _ {n+1} \mid X _ {n} = s] \le (1 - \delta)s$가 성립한다고 하자.

이 때, $\Pr[X _ {n} \ge 1 \mid X _ {0} = s] < e^{-\delta n} \cdot s$.

Proof. Markov’s inequality에 의해 $\Pr[X _ {n} \ge 1 \mid X _ {0} = s] \le \mathbb{E}[X _ {n} \mid X _ {0} = s]$이 성립하므로, $\mathbb{E}[X _ {n} \mid X _ {0} = s] \le (1 - \delta)^{n}s \le e^{-\delta n}s$. $\square$

이제 multiplicative drift가 존재한다는 것을 보이겠습니다. $k = \log(100)$으로 구태여 잡은 것은 $G^{+(W _ {t} - \Delta _ {t})}$에 음수 사이클이 없음에도 $\phi$를 못 찾을 확률이 $0.01$ 이하가 되도록 하여 $\mathbb{E}[D _ {t}]$를 관리하기 위함입니다.

먼저, 각 경우에 대해 $W _ {t+1}, \Delta _ {t+1}$이 어떻게 변화하는지 보면

Proposition. 만약 $\mathrm{Step}(k)$가 어떤 potential $\phi$를 반환했다면 $G _ {t+1} = (G _ {t}) _ {\phi}$, $W _ {t+1} \le W _ {t} - \frac{\Delta _ {t}}{4}$이고, $\Delta _ {t+1} = \Delta _ {t} / 4$.

Proposition. 만약 $\mathrm{Step}(k)$가 실패했다면, $W _ {t+1} = W _ {t}, \Delta _ {t+1} = \max(1, \Delta _ {t} / 2)$, 그리고 $D _ {t+1} \le 2D _ {t}$.

위의 proposition들은 어렵지 않게 증명할 수 있습니다. 이제 $D _ {t+1}$의 기댓값을 봅시다.

Case 1. $2\Delta _ {t} \ge (W _ {t} - M)$. 이 경우 $D _ {t} = (W _ {t} - M)^{19} \cdot 2\Delta _ {t}$가 되고,

• Case 1a. $\mathrm{Step}(k)$가 $\phi$를 반환한 경우, $D _ {t+1}$도 마찬가지로 $(W _ {t+1} - M)^{19} \cdot 2 \Delta _ {t+1}$이 됩니다. $W _ {t+1} - W _ {t} \le -\frac{\Delta _ {t}}{4} \le -\frac{1}{8}(W _ {t} - M)$에서, $D _ {t+1} \le 0.875^{19} \cdot 2D _ {t} < 0.16D _ {t}$를 얻습니다.

• Case 1b. $\mathrm{Step}(k)$가 Negcycle을 반환한 경우, 다음의 두 경우로 나눠 생각할 수 있습니다.

  • $\Delta _ {t} \le W _ {t} - M$: 실제로 negative cycle이 없지만 NegCycle을 반환한 경우로, 확률이 $0.01$에 불과하고 $D _ {t+1} \le 2D _ {t}$가 성립합니다.
  • $\Delta _ {t} > W _ {t} - M$: 실제로 negative cycle이 있는 경우입니다. $\Delta _ {t} \ge 2$가 항상 보장되고, $\Delta _ {t+1} = \Delta _ {t} / 2$를 보장할 수 있습니다. $D _ {t+1} = (W _ {t+1} - M)^{19} \cdot 2\Delta _ {t+1} = (W _ {t} - M)^{19} \cdot \Delta _ {t} = 0.5D _ {t}$.

따라서 Case 1의 경우 $\mathbb{E}[D _ {t+1} \mid D _ {t}]$를 생각하면 $\max(0.99 \cdot 0.16D _ {t} + 0.01 \cdot 2 D _ {t}, 0.5D _ {t})$로 bound됩니다.

Case 2. $2\Delta _ {t} < (W _ {t} - M)$. 이 경우 $D _ {t} = (W _ {t} - M)^{21} / 2\Delta _ {t}$가 됩니다. 아주 당연하게 $\mathrm{Step}(k)$가 성공해야 하는 상황이고, 실패할 확률은 $0.01$입니다. 이제 성공하는 케이스에 대해 case analysis를 하면

• Case 2a. $2\Delta _ {t+1} < W _ {t+1} - M$인 경우 $D _ {t+1} \le \frac{D _ {t}}{2}$가 됩니다. $W _ {t+1} - M \le W _ {t} - M$, $\Delta _ {t+1} = 2\Delta _ {t}$이니.
• Case 2b. $2\Delta _ {t+1} \ge W _ {t+1} - M$인 경우 $D _ {t+1} = (W _ {t+1} - M)^{19} \cdot 4\Delta _ {t}$가 됩니다. $(W _ {t+1} - M) - (W _ {t} -M) \le -\frac{\Delta _ {t}}{4} = -\frac{\Delta _ {t+1}}{8} \le -\frac{1}{16}(W _ {t+1} - M)$에서 $D _ {t+1} \le (16/17)^{19} \cdot (W _ {t} - M)^{19} \cdot 4\Delta _ {t}$를 얻습니다. 이 때 $8\Delta _ {t}^{2} < 2(W _ {t} - M)^{2}$에서, $4\Delta _ {t} \le \frac{2(W _ {t} - M)^{2}}{2\Delta _ {t}}$가 되니 결국 $D _ {t+1} \le (16/17)^{19} \cdot 2 D _ {t} \le 0.65D _ {t}$를 얻습니다.

따라서 Bayes theorem을 생각하면 $\mathbb{E}[D _ {t+1} \mid D _ {t}] \le 0.67D _ {t}$를 얻습니다.

Case 1, 2를 모두 생각하면 multiplicative drift를 얻을 수 있습니다. 굉장한 trial-and-error의 결과물로 저자들도 “technically involved”되어 있다고 표현한 만큼, 사실 이 글의 내용을 모두 다 가져가는 것은 의미가 없을지도 모르겠습니다. 결국은 가장 원하지 않는 케이스인 “음수 사이클은 없는데 shortest path tree는 찾지 못하는 경우”에 대한 대비가 slow case에선 되어 있지 않습니다. 한 번 이분탐색의 잘못된 갈래에 빠져들면 절대 지금의 상태보다 나아질 수 없는 것인데, 이 경우에는 $\Delta$를 줄이는 신중한 방식으로 접근하여, objective $D _ {t}$의 감소 경향성에 큰 영향을 미치지 않는 경우로 만들어낸 것입니다. 이러한 스타일의 문제들을 Noisy-binary search라고 이야기하는데, 여러 모로 응용 형태를 볼 수 있는 문제입니다.

Conclusion

두 글에 걸쳐 SSSP와 관련해 가장 최근의, 또 가장 좋은 결과를 내고 있는 randomized algorithm에 대해 다루었습니다. 사실 이 결과를 이용하여 그래프의 minimum cycle weight을 구하거나, strong low-diameter decomposition을 구하는 방법도 다루고 있으나 분량상 생략하였습니다.

이 논문의 지배적인 가정은 모든 가중치가 정수라는 것입니다. 일반적인 케이스에 대해서 적용되는 Bellman-ford보다 좋은 SSSP 알고리즘은 없을까요? 놀랍게도 이에 대해 굉장히 부정적인 결과가 5월에 출판되었습니다. 내용인즉 $d(u) \gets d(v) + w(v, u)$ (shortest path relaxation)의 sequence로 구성된 알고리즘은 determinisiic, randomized를 막론하고 Bellman-ford보다 좋을 수 없다는 내용인데, 꽤 권위 있는 저자의 논문인만큼 추후 다뤄보도록 하겠습니다.

Reference

• Bringmann, Karl, Alejandro Cassis, and Nick Fischer. “Negative-Weight Single-Source Shortest Paths in Near-Linear Time: Now Faster!.” arXiv preprint arXiv:2304.05279 (2023).
  • 오늘의 메인 논문입니다.
• Bernstein, Aaron, Danupon Nanongkai, and Christian Wulff-Nilsen. “Negative-weight single-source shortest paths in near-linear time.” 2022 IEEE 63rd Annual Symposium on Foundations of Computer Science (FOCS). IEEE, 2022.
  • 기존의 SOTA 논문인 BNW22로, 권위 있는 저널인 FOCS에 출판되었습니다. Bringmann23이 제시하는 대부분의 high-level structure가 이 논문에서 기인했습니다. 물론 Bringmann23은 충분히 self-contained되어 있어서 모두 읽을 필요까지는 없습니다.

• Eppstein, David. “Lower Bounds for Non-Adaptive Shortest Path Relaxation.” arXiv preprint arXiv:2305.09230 (2023).

• Lengler, Johannes. “Drift analysis.” Theory of evolutionary computation: Recent developments in discrete optimization (2020): 89-131.