2023 SCON
개요
지난 5월 20일에 진행된 2023 SCON이 성공적으로 종료되었습니다.
SCON은 Soongsil Programming Contest의 약자로, 숭실대학교 IT대학 재학생들을 대상으로 하는 ICPC 성격의 3인 팀 대회입니다.
이 글에서는 2023 SCON에 출제된 문제의 풀이에 대해서 다룹니다. 대회 개최와 운영에 관한 이야기는 운영진의 블로그(링크)에서 확인하실 수 있습니다.
문제 목록
대회에는 아래 목록의 10문제가 사용되었고, 저는 이 중에서 3문제(E,F,I)를 출제했습니다.
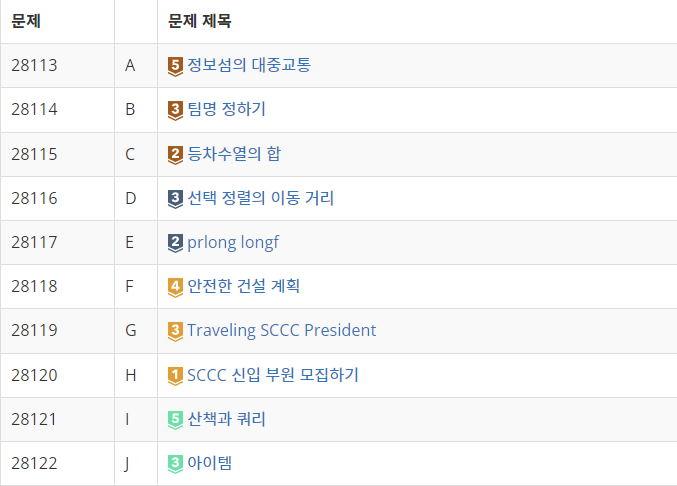
SCON에는 competitive programming 분야에 익숙하지 않은 학생들이 다수 참가하며 대회 시간이 3시간으로 짧은 편이고, 교내 ICPC 수상자가 모두 출제진으로 빠졌음을 고려해 문제들의 난이도를 전반적으로 낮게 설정했습니다. 또한, ICPC와 달리 문제 순서를 뒤섞지 않고 출제진이 예상한 난이도의 오름차순으로 배치했습니다.
BOJ에 업로드된 전체 문제 목록을 (링크)에서 확인하실 수 있습니다.
A. 정보섬의 대중교통
$N \leq B$이므로 $N$은 답에 영향을 주지 않습니다. 따라서 $A$와 $B$의 대소 관계만으로 답을 결정하면 됩니다.
solved.ac에서는 Bronze V로 책정되었고 실제로도 가장 쉬운 문제로 의도했기 때문에, 약간의 함정이 있음에도 본 대회에 참가한 모든 팀이 이 문제를 해결했습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
int N, A, B;
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin >> N >> A >> B;
if (A < B) cout << "Bus\n";
else if (A > B) cout << "Subway\n";
else cout << "Anything\n";
return 0;
}
B. 팀명 정하기
지문에서 주어진 조건을 그대로 구현하면 되는 문제입니다. 팀원이 3명만 주어지기 때문에 정렬 알고리즘을 모르더라도 간단한 조건문으로 정렬할 수 있습니다.
모든 팀이 해결하기를 바랐지만 아쉽게도 한 팀이 정렬 구현을 실수해서 33팀 중에 32팀이 해결해 주었습니다.
여담으로 예제에서 등장한 두 팀은 2020 & 2021 ICPC 수상팀인 181920과 2022 ICPC 수상팀인 NLP로, 저는 두 팀에서 각각 19와 L을 담당했습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
int N;
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
vector<string> res;
vector<pair<int, char> > ans;
for(int i=0; i<3; i++)
{
int p, y;
string s;
cin >> p >> y >> s;
res.push_back(to_string(y%100));
ans.push_back({p, s[0]});
}
sort(res.begin(), res.end());
sort(ans.rbegin(), ans.rend());
for(auto s : res)
cout << s;
cout << "\n";
for(auto [x,c] : ans)
cout << c;
cout << "\n";
return 0;
}
C. 등차수열의 합
다음의 두 가지 사실을 관찰하면 해결할 수 있습니다.
- 두 등차수열의 합은 등차수열이므로, 답이 되는 $B,C$가 존재함은 $A$가 등차수열임과 동치이다.
- $B = A, C = (0, 0, \cdots, 0)$으로 설정해도 된다.
33팀 중에 30팀이 해결해 주었습니다. B번 문제를 해결하지 못한 유일한 팀이 13번의 시도 끝에 이 문제를 해결한 덕분에 모든 팀이 2문제 이상을 해결했습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
int N;
int A[100101];
int main()
{
cin >> N;
for(int i=1; i<=N; i++)
cin >> A[i];
for(int i=3; i<=N; i++)
if (A[i-1]-A[i-2] != A[i]-A[i-1])
{
cout << "NO\n";
return 0;
}
cout << "YES\n";
for(int i=1; i<=N; i++)
cout << A[i] << " ";
cout << "\n";
for(int i=1; i<=N; i++)
cout << 0 << " ";
cout << "\n";
return 0;
}
D. 선택 정렬의 이동 거리
$A$가 순열이므로 역함수 $A^{-1}$을 정의할 수 있습니다. $i$번째 동작에서는 값 $i$와 값 $A_i$의 위치를 교환해 주면 되고, 특정 값의 위치를 찾는 작업은 $A^{-1}$을 이용해 $O(1)$에 수행할 수 있으므로 전체 문제가 $O(N)$에 해결됩니다.
33팀 중에 14팀이 해결해 주었습니다.
Open Contest에서는 D번이 E번보다 더 많이 풀렸고 solved.ac에서도 D번이 E번보다 더 쉬운 난이도로 책정되었지만, 예상 외로 본 대회에서는 D번이 더 적게 풀렸습니다. 아마도 그 이유로는 예상보다 inverse permutation에 대한 관찰이 까다로운 편이었으며, 시간복잡도 개념이 익숙하지 않아 $O(N^2)$ 선택 정렬을 실제로 구현한 팀이 많았기 때문인 것으로 생각됩니다. (D번에 대한 제출 중 68%가 시간 초과였습니다.)
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
int N;
int A[500001], P[500001], res[500001];
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin >> N;
for(int i=1; i<=N; i++)
{
cin >> A[i];
P[A[i]] = i;
}
for(int i=1; i<=N; i++)
if (A[i] != i)
{
int x = A[i], y = i; // 값 x와 y의 위치를 swap한다.
res[x] += abs(P[x] - P[y]);
res[y] += abs(P[x] - P[y]);
swap(P[x], P[y]);
A[P[x]] = x;
A[P[y]] = y;
}
for(int x=1; x<=N; x++)
cout << res[x] << " ";
cout << "\n";
return 0;
}
E. prlong longf
제가 출제한 문제로, 팩토리얼 2 문제를 풀다가 떠올렸습니다. 처음에는 $O(N)$ 풀이를 기준으로 제안했지만, 이후 시간복잡도 개념이 익숙하지 않은 참가자들을 위해 $N$ 제한을 대폭 줄였습니다.
33팀 중에 17팀이 해결해 주었습니다.
풀이 1. 완전 탐색
longlong을 int로 변환한다고 거꾸로 생각할 수 있습니다.
$N \leq 80$으로 제한이 매우 작아 문자열 내에 long이 최대 20번 등장합니다. 따라서 가능한 모든 경우를 완전 탐색으로 열거하는 $O(2^{N/4} \cdot N)$ 풀이가 통과합니다.
실제로는 답의 상한이 피보나치 수 $F_{N/4}$에 근사하고, 재귀 호출을 $4(F_1 + F_2 + \cdots + F_{N/4}) + F_{N/4+1} = 4(F_{N/4+2} - 1) + F_{N/4+1}$번 이하로 수행하므로 더 작은 시간복잡도인 $O({1.618}^{N/4})$를 갖는다는 사실을 알 수 있습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
int N;
string s;
int f(int i)
{
if (i >= s.size()) return 1;
int ret = f(i+1);
if (s.substr(i, 8) == "longlong") ret += f(i+8);
return ret;
}
int main()
{
cin >> N >> s;
cout << f(0) << "\n";
return 0;
}
풀이 2. DP
예제 3의 longlongdoublelonglong처럼 분리되어 있는 long...은 서로 독립이므로, 연속한 long...마다 경우의 수를 따로 계산한 뒤 모두 곱하면 됩니다.
$D[n]$을 long이 $n$개 연속으로 붙어 있는 문자열을 복원하는 경우의 수라고 정의하면, $D[0] = D[1] = 1, D[n] = D[n-1] + D[n-2]$라는 점화식이 성립합니다.
따라서 DP로 $O(N)$에 해결할 수 있습니다.
위 점화식은 피보나치 수의 점화식과 동일하며, DP 기본 문제에 피보나치 수와 유사한 점화식이 많아서인지 이 풀이로 해결한 팀도 많았습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
int N, F[21];
string s;
int main()
{
F[0] = F[1] = 1;
for(int i=2; i<=20; i++)
F[i] = F[i-1] + F[i-2];
cin >> N >> s;
int res = 1;
for(int i=0; i<s.size(); i++)
{
int cnt = 0;
while (s.substr(i, 4) == "long") cnt++, i += 4;
res *= F[cnt];
}
cout << res << "\n";
return 0;
}
F. 안전한 건설 계획
제가 출제한 문제입니다. 처음에는 $O(N+M)$ 풀이를 기준으로 제안했지만, 그리디 풀이를 추가로 발견한 후에 E번 문제와 동일한 이유 + 그래프 탐색 알고리즘이나 인접 리스트를 모르더라도 해결할 수 있도록 $N$ 제한을 대폭 줄였습니다.
33팀 중에 8팀이 해결해 주었습니다.
풀이 1. 그리디
비용이 적게 드는 연산부터 진행하는 그리디 전략이 성립합니다.
완전 그래프가 될 때까지 아래 과정을 반복합시다.
-
비용이 0인 보강 작업을 사용할 수 있다면, 아무거나 하나 찾아서 진행한다.
-
그렇지 않다면, 비용이 1인 보강 작업을 아무거나 하나 찾아서 진행한다.
매번 수행할 보강 작업을 $O(N^3)$에 찾을 수 있고, 보강 작업은 $O(N^2)$번 진행하므로 최종 시간복잡도는 $O(N^5)$가 됩니다.
$N$ 제한이 매우 작아서 그래프를 인접 리스트 대신에 (초심자가 더 생각해내기 쉬운)인접 행렬에 저장할 수 있고, 엄밀한 증명을 하지 않더라도 찍어 맞추기가 쉬운 편이라서인지 75%의 팀이 이 풀이로 해결했습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
int N, M, res;
int g[41][41];
bool Try(int cost)
{
for(int i=1; i<=N; i++)
for(int j=i+1; j<=N; j++)
for(int k=j+1; k<=N; k++)
if (g[i][j] + g[j][k] + g[i][k] == 2-cost)
{
g[i][j] = g[j][k] = g[i][k] = 1;
res += cost;
return true;
}
return false;
}
int main()
{
cin >> N >> M;
for(int i=0; i<M; i++)
{
int a, b;
cin >> a >> b;
g[a][b] = 1;
}
while(Try(0) || Try(1));
cout << res << "\n";
return 0;
}
풀이 2. 그래프 탐색
정답의 상한과 하한을 찾아 봅시다.
관찰 1. 연결 그래프라면 0의 비용으로 완전 그래프로 만들 수 있습니다.
구성적 증명
$N \leq 2$인 연결 그래프는 이미 완전 그래프입니다.
$N \geq 3$이라면,
-
아무 간선 $(a,b)$를 찾아서, 정점 부분집합 $S = \lbrace a,b \rbrace$를 정의합니다.
-
$S$가 모든 정점을 포함할 때까지 다음 과정을 반복합니다: $u \in S, v \not \in S$인 간선 $(u,v)$를 찾고, $x \in S, x \neq u$인 정점 $x$마다 보강 작업 $(x,u,v)$를 진행한 후, $S$에 $v$를 추가합니다.
관찰 2. 연결 요소가 여러 개라면, 간선이 하나라도 있는 연결 요소 $A$와, $A \neq B$인 아무 연결 요소 $B$를 비용이 1인 보강 작업으로 연결할 수 있습니다. 따라서 정답의 상한은 (연결 요소의 개수) - 1입니다.
관찰 3. 비용이 0인 보강 작업은 연결 요소의 개수를 줄일 수 없고, 비용이 1인 보강 작업은 연결 요소의 개수를 최대 1만큼 줄일 수 있습니다. 따라서 정답의 하한은 (연결 요소의 개수) - 1입니다.
정답의 상한과 하한이 같으므로, 정답은 정확히 (연결 요소의 개수) - 1이 됩니다.
아무 그래프 탐색 알고리즘을 사용하면 $O(N^2)$에 해결할 수 있고, 여러 참가자가 DFS, BFS, Union-Find 등의 방법으로 해결했습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
int N, M;
vector<int> g[41];
bool vis[41];
void DFS(int n)
{
vis[n] = true;
for(int next : g[n])
if (!vis[next])
DFS(next);
}
int main()
{
cin >> N >> M;
for(int i=0; i<M; i++)
{
int a, b;
cin >> a >> b;
g[a].push_back(b);
g[b].push_back(a);
}
int cnt = 0;
for(int i=1; i<=N; i++)
if (!vis[i])
DFS(i), cnt++;
cout << cnt-1 << "\n";
return 0;
}
G. Traveling SCCC President
입력으로 들어오는 $A$는 함정입니다. 모든 정점을 한 번 이상 방문한 이후에는 $A$가 어떻게 주어졌는지와 무관하게 순간이동만으로 모든 회의를 순서대로 진행할 수 있습니다.
도로로 이동한 간선들은 연결 그래프를 이뤄야 하므로 정답의 하한은 MST의 가중치이고, 실제로도 MST에 속하는 간선만을 도로로 이동하는 해를 구성할 수 있습니다. 따라서 정답은 MST의 가중치가 됩니다.
33팀 중에 6팀이 해결해 주었습니다.
문제의 함정에 걸려들어서 $A$ 배열을 이용한 다익스트라를 구현하다가 WA를 받은 팀이 있었습니다. 또한, 주어진 지문에서 자연스럽게 프림 알고리즘을 떠올릴 수 있어서인지 프림 알고리즘으로 정답을 받은 팀이 생각보다 많았습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
int N, M, S;
int p[2020];
int Find(int n)
{
if (n == p[n]) return n;
return Find(p[n]); // slow find
}
void Union(int a, int b)
{
a = Find(a); b = Find(b);
if (a == b) return;
p[a] = b;
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin >> N >> M >> S;
for(int i=1; i<=N; i++)
p[i] = i;
vector<array<int, 3> > e;
for(int i=0; i<M; i++)
{
int a, b, c;
cin >> a >> b >> c;
e.push_back({c, a, b});
}
// ignore input A[]
sort(e.begin(), e.end());
int res = 0;
for(auto [c,a,b] : e)
{
if (Find(a) == Find(b)) continue;
Union(a, b);
res += c;
}
cout << res << "\n";
return 0;
}
H. SCCC 신입 부원 모집하기
33팀 중에 1팀이 해결해 주었습니다. 출제자의 기대와 달리 본 대회에서 정답을 받은 유일한 팀은 flow를 사용했고, Open Contest에서도 flow를 사용하지 않고 정답을 받은 참가자가 1명뿐이었습니다.
검수 중에 백트래킹에서 잘못된 커팅을 하는 솔루션을 만들었는데, 스트레스 테스트로도 반례가 나오지 않아서 WA가 나오는 저격 데이터를 만드는 작업이 까다로웠습니다. 본 대회에서는 데이터가 충분히 강했던 것 같아서 다행입니다.
풀이 1. bitmask DP
점수가 높은 사람부터 차례대로 배정합니다.
각 스터디 그룹 $i$의 정원이 $C_i$만큼 남았을 때, 현재 인원의 상태를 $C = (C_1, C_2, \cdots, C_K)$라는 배열로 표현할 수 있습니다.
아래 DP를 채운 다음, 배정 방법이 존재하는 $D[N][*]$를 아무거나 선택해서 출력하면 됩니다.
$D[i][C] = i$번째 사람까지 배정해서 인원의 상태가 $C$가 되게 하는 최적의 배정이 존재하는가? 존재한다면 그러한 배정 방법을 아무거나 하나 저장한다.
$i$의 범위는 $[1,N]$이고 $C$의 각 원소의 범위는 $[0,X]$이므로, $C$는 $X+1$진법을 이용해 $0$ 이상 $(X+1)^K$ 미만의 정수 값으로 표현할 수 있습니다.
따라서 상태의 개수는 $O(N(X+1)^K)$이고, 상태 전이가 $O(K)$이므로 최종 시간복잡도는 $O(NK(X+1)^K)$가 됩니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
int N, K, X;
bool can[15][15];
vector<pair<int, int> > v;
int pw[15+1];
int dp[15+1][1<<15];
vector<int> res[15];
void f(int i, int j) // 역추적
{
if (i == N) return;
if (dp[i][j] == dp[i+1][j])
{
f(i+1, j);
return;
}
for(int k=0; k<K; k++)
if (can[v[i].second][k] && j/pw[k]%(X+1) < X) //
if (dp[i][j] == dp[i+1][j+pw[k]] + (1<<N-1-i))
{
res[k].push_back(v[i].second); //
f(i+1, j+pw[k]);
return;
}
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin >> N >> K >> X;
pw[0] = 1;
for(int k=1; k<=K; k++)
pw[k] = pw[k-1] * (X+1);
for(int i=0; i<N; i++)
{
int x, y;
cin >> x;
while(x--)
{
cin >> y;
y--; // 0-based
can[i][y] = true;
}
}
for(int i=0; i<N; i++)
{
int x;
cin >> x;
v.push_back({x, i});
}
sort(v.rbegin(), v.rend());
for(int i=N-1; i>=0; i--)
for(int j=0; j<pw[K]; j++)
{
// dp[i][j] : i번째를 고를 차례인데 현재 bit의 상태가 j일 때, 이후 추가로 얻을 수 있는 점수의 최댓값
dp[i][j] = dp[i+1][j];
for(int k=0; k<K; k++)
if (can[v[i].second][k] && j/pw[k]%(X+1) < X) //
dp[i][j] = max(dp[i][j], dp[i+1][j+pw[k]] + (1<<N-1-i));
}
f(0, 0);
for(int k=0; k<K; k++)
{
cout << res[k].size() << " ";
for(int i : res[k])
cout << i+1 << " ";
cout << "\n";
}
return 0;
}
풀이 2. MCMF
점수가 $i$번째로 높은 사람의 가중치를 $2^{N-i}$로 두면 최대 가중치 매칭 문제가 됩니다. 정점이 $O(N+K)$개, 간선이 $O(NK)$개, flow가 $O(N)$이므로, MCMF나 Hungarian Algorithm 등으로 $O(N^3K + N^2K^2)$에 해결할 수 있습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
template<class Cost> struct MCMF {
struct Edge { int next, rev, cap; Cost cost; };
int N;
vector<vector<Edge> > g;
vector<Cost> dual;
MCMF(int n) : N(n), g(n), dual(n) {}
void AddEdge(int a, int b, int cap, Cost cost) {
g[a].push_back({ b, (int)g[b].size(), cap, cost });
g[b].push_back({ a, (int)g[a].size() - 1, 0, -cost });
}
void MakePositive(int src, int snk) { // 초기 그래프에 음수 가중치가 없으면 필요 없다.
vector<Cost> dist(N, numeric_limits<Cost>::max() / 2);
vector<bool> inq(N), vis(N);
queue<int> q; q.push(src); dist[src] = 0; inq[src] = true;
while (!q.empty()) {
int n = q.front(); q.pop(); inq[n] = false; vis[n] = true;
for (auto &e : g[n]) {
if (e.cap && dist[e.next] - dist[n] > e.cost) {
dist[e.next] = dist[n] + e.cost;
if (!inq[e.next]) q.push(e.next), inq[e.next] = true;
}
}
}
for (int n = 0; n < N; n++) {
if (!vis[n]) continue;
dual[n] -= dist[snk] - dist[n];
}
}
pair<int, Cost> Run(int src, int snk, int upper = 1234567890) {
MakePositive(src, snk);
vector<Cost> dist(N);
vector<int> p(N), pp(N);
vector<bool> vis(N);
auto dual_ref = [&]() {
fill(dist.begin(), dist.end(), numeric_limits<Cost>::max() / 2);
fill(p.begin(), p.end(), -1);
fill(pp.begin(), pp.end(), -1);
fill(vis.begin(), vis.end(), false);
struct Node {
Cost cost; int n;
bool operator<(Node r) const { return cost > r.cost; }
};
priority_queue<Node> pq;
pq.push({ 0, src }); dist[src] = 0;
while (!pq.empty()) {
int n = pq.top().n; pq.pop();
if (vis[n]) continue;
vis[n] = true;
if (n == snk) break;
for (int i = 0; i < g[n].size(); i++) {
auto e = g[n][i];
if (vis[e.next] || !e.cap) continue;
Cost cost = e.cost - dual[e.next] + dual[n];
if (dist[e.next] - dist[n] > cost) {
dist[e.next] = dist[n] + cost;
p[e.next] = n; pp[e.next] = i;
pq.push({ dist[e.next], e.next });
}
}
}
if (!vis[snk]) return false;
for (int n = 0; n < N; n++) {
if (!vis[n]) continue;
dual[n] -= dist[snk] - dist[n];
}
return true;
};
int flow = 0;
Cost cost = 0;
while (flow < upper) {
if (!dual_ref()) break;
int c = upper - flow;
for (int n = snk; n != src; n = p[n])
c = min(c, g[p[n]][pp[n]].cap);
Cost d = -dual[src];
for (int n = snk; n != src; n = p[n]) {
auto& e = g[p[n]][pp[n]];
e.cap -= c; g[n][e.rev].cap += c;
}
flow += c; cost += c * d;
}
return { flow, cost };
}
};
int N, K, X;
bool can[15][15];
int p[15][15];
vector<pair<int, int> > v;
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin >> N >> K >> X;
MCMF<int> mcmf(N+K+2);
int src = N+K, snk = N+K+1;
for(int i=0; i<K; i++)
mcmf.AddEdge(i+N, snk, X, 0);
for(int i=0; i<N; i++)
{
int x, y;
cin >> x;
while(x--)
{
cin >> y;
y--; // 0-based
can[i][y] = true;
p[i][y] = mcmf.g[i].size();
mcmf.AddEdge(i, N+y, 1, 0);
}
}
for(int i=0; i<N; i++)
{
int x;
cin >> x;
v.push_back({x, i});
}
sort(v.rbegin(), v.rend());
for(int i=0; i<N; i++)
mcmf.AddEdge(src, v[i].second, 1, -(1<<N-i)); // '최소' 가중치 '최대' 매칭
mcmf.Run(src, snk);
for(int k=0; k<K; k++)
{
vector<int> res;
for(int i=0; i<N; i++)
if (can[i][k] && mcmf.g[i][p[i][k]].cap == 0)
res.push_back(i);
cout << res.size() << " ";
for(int i : res)
cout << i+1 << " ";
cout << "\n";
}
return 0;
}
풀이 3. 이분 매칭
현재까지 매칭된 사람의 집합에 $i$번째 사람을 추가할 수 있는지는 이분 매칭으로 확인 가능합니다. 따라서 Kuhn’s Algorithm이나 Ford-Fulkerson Algorithm 등으로 $O(N^2K)$에 해결할 수 있습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
#define FLOW_MAX 1234567890
template<class Cap> struct Dinic {
struct Edge { int next, rev; Cap c, f; };
int N;
vector<vector<Edge> > g;
vector<int> lv, work;
queue<int> q;
Dinic(int n) : N(n), g(n), lv(n), work(n) {}
void AddEdge(int a, int b, Cap c) {
g[a].push_back({ b, (int)g[b].size(), c, 0 });
g[b].push_back({ a, (int)g[a].size() - 1, 0, 0 });
}
Cap dfs(int n, int snk, Cap flow) {
if (n == snk) return flow;
for (int &i = work[n]; i < g[n].size(); i++) {
auto &e = g[n][i];
if (e.c - e.f > 0 && lv[e.next] == lv[n] + 1) {
Cap cost = dfs(e.next, snk, min(flow, e.c - e.f));
if (cost > 0) {
e.f += cost;
g[e.next][e.rev].f -= cost;
return cost;
}
}
}
return 0;
}
Cap Run(int src, int snk, Cap upper = FLOW_MAX) {
Cap ret = 0;
while (1) {
fill(lv.begin(), lv.end(), -1);
q.push(src); lv[src] = 0;
while (!q.empty()) {
int n = q.front(); q.pop();
for (auto &e : g[n])
if (e.c - e.f > 0 && lv[e.next] == -1)
q.push(e.next), lv[e.next] = lv[n] + 1;
}
if (lv[snk] == -1) break;
fill(work.begin(), work.end(), 0);
while (1) {
Cap flow = dfs(src, snk, upper - ret);
ret += flow;
if (flow == 0 || ret == upper) break;
}
if (ret == upper) break;
}
return ret;
}
};
int N, K, X;
bool can[15][15];
vector<pair<int, int> > v;
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin >> N >> K >> X;
Dinic<int> dinic(N+K+2);
int src = N+K, snk = N+K+1;
for(int i=0; i<N; i++)
dinic.AddEdge(src, i, 1);
for(int i=0; i<K; i++)
dinic.AddEdge(i+N, snk, X);
for(int i=0; i<N; i++)
{
int x, y;
cin >> x;
while(x--)
{
cin >> y;
y--; // 0-based
can[i][y] = true;
}
}
for(int i=0; i<N; i++)
{
int x;
cin >> x;
v.push_back({x, i});
}
sort(v.rbegin(), v.rend());
vector<vector<int> > p(N, vector<int>(K));
vector<vector<int> > res(K);
for(auto [x,i] : v)
{
for(int k=0; k<K; k++)
if (can[i][k])
{
p[i][k] = dinic.g[i].size();
dinic.AddEdge(i, k+N, 1);
}
dinic.Run(src, snk);
}
for(int i=0; i<N; i++)
for(int k=0; k<K; k++)
if (can[i][k] && dinic.g[i][p[i][k]].f)
res[k].push_back(i);
for(int k=0; k<K; k++)
{
cout << res[k].size() << " ";
for(int x : res[k])
cout << x+1 << " ";
cout << "\n";
}
return 0;
}
I. 산책과 쿼리
제가 출제한 문제입니다. 2020 ICPC 예선에 출제된 사이클 게임에 아이디어를 추가한 뒤, 오프라인 쿼리 + 이분 탐색으로 풀리지 않게 하고 싶어서 만들게 되었습니다. 어떻게든 Union-Find 없이 오프라인으로 해결하고 싶다면 Offline Incremental SCC와 비슷한 아이디어로 분할 정복을 하면 될 것 같은데 구현해 보지는 않았습니다… 또한 DFS + 양방향 탐색도 가능해 보이지만 역시 구현하지는 않았습니다.
먼저, 어떤 자취방 $u$에 대해 $u$의 산책의 자유도가 높은지 판별할 방법을 생각해 봅시다.
-
$u$에 산책로가 하나라도 붙어 있다면, $(u,v)$를 왕복해서 모든 짝수 시각을 만들 수 있습니다.
-
적당히 짧은 홀수 시간 산책 방법이 하나라도 존재한다면, 이후 $(u,v)$를 왕복해서 충분히 큰 모든 홀수 시각을 만들 수 있습니다.
이제 홀수 시간 산책의 존재성을 판별하는 문제로 바뀌었습니다.
짝수 시각을 낮, 홀수 시각을 밤이라고 생각하고, 1의 시간이 지날 때마다 낮과 밤이 뒤바뀐다고 생각해 봅시다. 각 정점 $u$를 $u_\textrm{day}$와 $u_\textrm{night}$로 쪼개서 생각할 수 있습니다.
만약 어떠한 $x$에 대해 $x_\textrm{day}$에서 $x_\textrm{night}$로 갈 수 있다면, $x$를 포함하는 연결 요소 내의 모든 자취방 $u$는 홀수 시간 산책 방법이 존재하게 됩니다. 이러한 $x$를 포함하는 연결 요소를 “홀수 연결 요소”라고 부릅시다. 홀수 연결 요소 내의 모든 자취방은 정답에 1씩 기여하게 됩니다.
쿼리 $(a,b)$가 주어질 때마다,
-
$(a_\textrm{day}, b_\textrm{night})$를 연결하고, $(a_\textrm{night}, b_\textrm{day})$를 연결합니다.
-
$a_\textrm{day}$와 $a_\textrm{night}$가 연결되어 있다면, 이 연결 요소를 홀수 연결 요소로 설정합니다.
위 작업은 각 집합마다 size를 관리하는 Union-Find 자료구조로 $O(N + Q \alpha(N))$에 해결할 수 있습니다.
33팀 중에 1팀이 해결해 주었습니다. 본 대회에서 이 문제를 유일하게 해결한 팀은 small to large로 구현한 데다 fastio를 깜박해서 TLE를 받길래 걱정했지만, 다행히 금방 고치고 정답을 받았습니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
int N, Q, res;
int p[600001], sz[600001];
int Not(int n)
{
if (n <= N) return n+N;
return n-N;
}
int Find(int n)
{
if (n == p[n]) return n;
return p[n] = Find(p[n]);
}
void Union(int a, int b)
{
a = Find(a); b = Find(b);
if (a == b) return;
if (a == Find(Not(a))) res -= sz[a];
if (b == Find(Not(b))) res -= sz[b];
p[b] = a;
sz[a] += sz[b];
if (a == Find(Not(a))) res += sz[a];
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin >> N >> Q;
for(int i=1; i<=N+N; i++)
p[i] = i, sz[i] = (i <= N);
while(Q--)
{
int a, b;
cin >> a >> b;
Union(a, Not(b));
Union(b, Not(a));
cout << res << "\n";
}
return 0;
}
J. 아이템
더 어려운 문제들은 대회의 난이도를 낮추기 위해 잘려나가서 이 문제가 최고 난이도로 준비되었습니다. 본 대회에서는 해결한 팀이 없지만, Open Contest에서는 여러 참가자가 해결해 주었습니다.
아이템의 좌표를 이진법으로 생각하면, 아이템을 획득할 때마다 이동할 수 있는 좌표가 최하위 비트부터 하나씩 고정됩니다. 따라서 아이템의 좌표를 최하위 비트부터 삽입한 이진 트라이를 만들고 생각할 수 있습니다.
이제 트라이의 루트에서부터 시작해서 아래로 한 칸 이동한 뒤 서브트리 내의 아이템 하나를 획득하는 행동을 반복하는 문제가 되었습니다.
정점 $n$의 서브트리에 있는 아이템의 개수를 $S[n]$이라 정의합시다. 이 값은 아이템을 트라이에 삽입하는 과정에서 구할 수 있습니다.
아래로 한 칸 이동해 $n$에 도착했을 때, $n$의 서브트리에서 얻을 수 있는 아이템의 최대 개수를 $D[n]$이라 정의합시다.
$D[\textrm{leaf}] = S[\textrm{leaf}], D[n] = \max(D[n.l] + I(D[n.l] < S[n]), D[n.r] + I(D[n.r] < S[n]))$라는 점화식으로 나타낼 수 있습니다. 여기서 $I(x)$는 indicator function으로, $x$의 값이 참이면 $1$, 거짓이면 $0$을 반환합니다.
따라서 $O(N \log \max(X_i))$에 전체 문제가 해결됩니다. 출제자의 풀이는 DP 대신에 DFS 한 번으로 답을 구하는데, DP 풀이와 유사하므로 생략합니다.
제가 작성한 코드는 아래와 같습니다.
#include<bits/stdc++.h>
using namespace std;
#define INF 1234567890
#define ll long long
struct Node {
int g[2], cnt, dp;
bool leaf;
Node() { g[0] = g[1] = cnt = dp = leaf = 0; }
};
vector<Node> trie(2);
void Insert(int n, int k, ll x)
{
trie[n].cnt++;
if (k == 0)
{
trie[n].leaf = true;
return;
}
if (trie[n].g[x%2] == 0) trie[n].g[x%2] = trie.size(), trie.push_back(Node());
Insert(trie[n].g[x&1], k-1, x/2);
}
int N, res;
void DFS(int n)
{
if (n == 0) return;
if (trie[n].leaf) trie[n].dp = trie[n].cnt;
for(int i=0; i<2; i++)
{
DFS(trie[n].g[i]);
trie[n].dp = max(trie[n].dp, trie[trie[n].g[i]].dp + (trie[trie[n].g[i]].dp < trie[n].cnt));
}
if (n != 1) res = max(res, trie[n].dp);
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin >> N;
for(int i=1; i<=N; i++)
{
ll x;
cin >> x;
Insert(1, 60, x);
}
DFS(1);
cout << res << "\n";
return 0;
}