ho94949's profile image

ho94949

June 21, 2023 00:00

서론

(무향) 그래프 $G$는 정점 집합 $V$와 간선 집합 $E$ 로 이루어진 구조입니다. 간선은 두 원소를 잇는 (순서가 없는) 선입니다. 여기서 그래프의 정점을 색칠한 다는 것은, 간선의 양 끝이 다른 색이 되도록 색칠한다는 것입니다이 게시글에서는 그래프 색칠에 대한 다양한 주제를 다룹니다. 해당 주제는 그래프 색칠에 대한 시각을 늘려줄 것이라고 생각합니다. 다룰 주제는 다음과 같습니다.

주제

• 이분그래프 색칠
• 그리디 색칠, $(\Delta+1)$색 정리, $6$색 정리
• $5$색 정리, $4$색 정리, Kempe Chain, $\Delta$색 정리
• 채색 다항식

표기법

이 게시글에서는 다음과 같은 표기법을 사용합니다.

• 두 집합 $A, B$의 차집합을 $A \setminus B = {x \in A \mid x \not \in B}$로 표시합니다.
• 그래프(Graph)를 $G = (V, E)$ 로 표현하고, 정점(Vertex) 집합을 $V$, 간선(Edge) 집합을 $E$ 라고 표현합니다.
  • $V$는 아무 집합이나 될 수 있습니다. ¹
  • $E$는 크기 $2$ 인 $V$ 의 부분집합을 원소로 가지는 집합입니다.
• 정점 $v$의 이웃(Neighbour)을 $N_G(v)$ 라고 표현합니다. $v$의 이웃은 $v$와 간선으로 이어진 정점의 집합을 말합니다.
  • 엄밀히 말해서, $N_G(v) = { u \mid {u, v} \in E}$입니다. 맥락에 따라 $G$를 생략하기도 합니다.
• 정점 $v$의 차수(Degree)를 $\delta_G(v)$ 라고 표현합니다. $v$의 차수는 $v$의 이웃의 수입니다.
  • 즉, $\delta_G(v) = \lvert N_G(v) \rvert$입니다. 맥락에 따라 $G$를 생략하기도 합니다.
• 그래프의 차수 중 최댓값을 $\Delta(G)$로 표현합니다.
  • 즉, $\delta(G) = \max_{v \in V} \delta(v)$ 입니다.
• 그래프에서 경로(Path) $P$ 는 $(v_1, e_1, v_2, e_2, \cdots, v_p, e_p, v_{p+1})$로 표현 되는, $e_i$ 의 양 끝점이 $v_i$ 와 $v_{i+1}$ 인 것입니다. 이를 길이 $p$의 $v_1$ 과 $v_{p+1}$를 잇는 경로라고 합니다.
• 그래프가 연결그래프(Connected Graph)라는 것은 임의의 두 정점 $u, v \in V$ 에 대해 $u$와 $v$를 잇는 경로가 존재한다는 것입니다.
• 그래프의 채색(Graph-coloring)은 그래프의 각 정점에 양의 정수 하나를 대응시켜서 간선의 양 끝이 다른 색이 되도록 색칠하는 것입니다.
  • 즉, $f: V \rightarrow \mathbb Z^+$이고 ${u, v} \in E$ 에 대해 $f(u) \ne f(v)$입니다.
  • 이 그래프의 채색에 사용한 색의 수는 $\max f$ 로 정의합니다.
• 그래프의 채색수는 그래프를 칠하는데 필요한 최소한의 색을 채색수(Chromatic Number)라고 합니다. 이는 $\chi(G)$ 로 표현합니다.
• $k \ge \chi(G)$ 에 대해 그래프는 $k$가지 색으로 칠할 수 있습니다. ($k$-colorable)
• 정점 $V$의 부분집합 $S$에 대해 $G$의 유도된 부분그래프(Induced Subgraph) $G[S]$는 정점을 $V$로 하고, 양쪽 끝이 $S$에 속한 간선을 모두 가져와 만든 그래프입니다.

이분그래프의 색칠

이분그래프(Bipartite Graph)란, $V$ 를 두 개의 부분집합 $L$과 $R$로 나누어서, 간선의 양 끝이 $L$에서 하나, $R$에서 하나씩 골라서 잇도록 할수 있는 그래프입니다. 즉, $V = L \cup R, L \cap R = \phi$이고 $e \in E$ 에 대해 $e \cap L \ne \phi, e \cap R \ne \phi$ 로 $L$과 $R$을 나눌 수 있다면 이 그래프는 이분그래프입니다. $L$에 있는 정점을 $1$, $R$에 있는 정점을 $2$번 색으로 칠하면 색칠과도 관련이 있습니다. 이제 다음 명제를 증명합시다.

Claim. 이분그래프와 $\chi(G) \le 2$ 인것은 동치입니다.

Proof. 채색 $f$ 에 대해, $L = {v \mid f(v) = 1}, R = {v \mid f(v) = 2}$ 를 사용하면, 나머지는 채색과 이분그래프의 정의에 의해 쉽게 증명이 됩니다. $\square$

비슷한 방식으로 우리가 $V$를 $L$, $R$의 두 개가 아니라 $V_1, \cdots, V_k$로 나눈다고 하면 이 그래프를 $k$분그래프($k$-partite graph)라고 하고, 역시 $\chi(G) \le k$ 와 동치입니다.

이제 그래프를 $2$개의 색으로 색칠해 봅시다. 그래프가 연결그래프가 아닌 경우 각 성분을 색칠하는 것으로 괜찮습니다. 일반성을 잃지 않고 $G$가 연결그래프이고, 그래프의 한 정점 $v_1$ 이 $1$로 색칠된다고 합시다. 그러면,

• $v_1$과 이어진 모든 정점은 $1$이 아닌 유일한 2로 색칠해야합니다.
• 마찬가지로, $2$로 색칠된 정점과 이어진 모든 정점은 유일한 색인 $1$로 색칠해야합니다.

즉, $G$의 $v_1$의 색을 정하면, 나머지 색은 그래프 탐색을 하면서 이전에 방문한 인접한 정점의 색의 반대 색으로 칠하기만 하면 됩니다. 이 과정으로 칠하면서 모순되는 점이 있다면, 두 색으로 칠할 수 없으니 주어진 그래프는 이분그래프가 아닙니다.

삼분그래프의 색칠

아쉽게도, $\chi(G) \ge 3$ 인 그래프는 위 방식으로 칠할 수 없습니다. 또한, 이런 그래프의 채색수를 찾는 문제는 NP-Complete인 것이 증명되어 있습니다.

연습문제

실제로 이분그래프의 색칠을 구현해봅시다.

• BOJ 1707 이분 그래프

그리디 색칠

기본적으로 그래프를 색칠하는 아이디어는, 그리디하게 색을 칠하는 것입니다. 과정은 다음과 같습니다.

1. $V$의 원소들을 원하는 순서 $v_1, v_2, \cdots, v_{\lvert V \rvert} $로 나열합니다.
2. $f(v_i)$ 를 하나씩 정해나갑니다. $f(v_i)$의 값은, 이전에 칠했던 색과 모순되지 않는 가장 최소의 색입니다. 즉, $f(v_i) = \min\left(\mathbb Z^+ \setminus {f(u) \mid {u, v} \in E}\right)$입니다.

그리디 색칠을 이용해서, 가장 기본적인 정리를 증명해봅시다.

$(\Delta+1)$색 정리

Claim. $\chi(G) \le \Delta(G) + 1$. 즉, 그래프의 채색수는 그 그래프가 가지고 있는 최고 차수 $ + 1$ 이하입니다.

Proof. 그리디 색칠 알고리즘을 사용합시다. $f(v_i)$ 를 결정 할 때, 최대 $\Delta(G)$ 개의 색을 피해야 하기 때문에, $f(v_i)$ 로 결정되는 값은 $\Delta(G)+1$을 넘지 않습니다. $\square$

하지만 이 $\chi(G)$ 가 언제나 $\Delta(G)+1$인 것은 아닙니다. 다음과 같은 예제를 봅시다.

그리디 색칠의 비최적성

Claim. 그리디 색칠 알고리즘을 사용해서 올바르게 채색수를 찾을 수 없는 그래프 $G$가 존재한다.

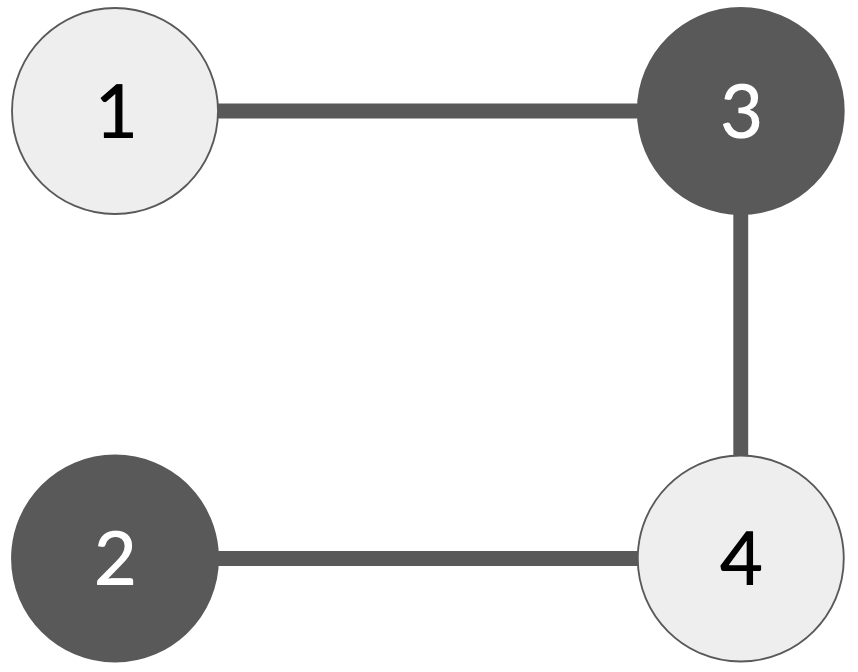
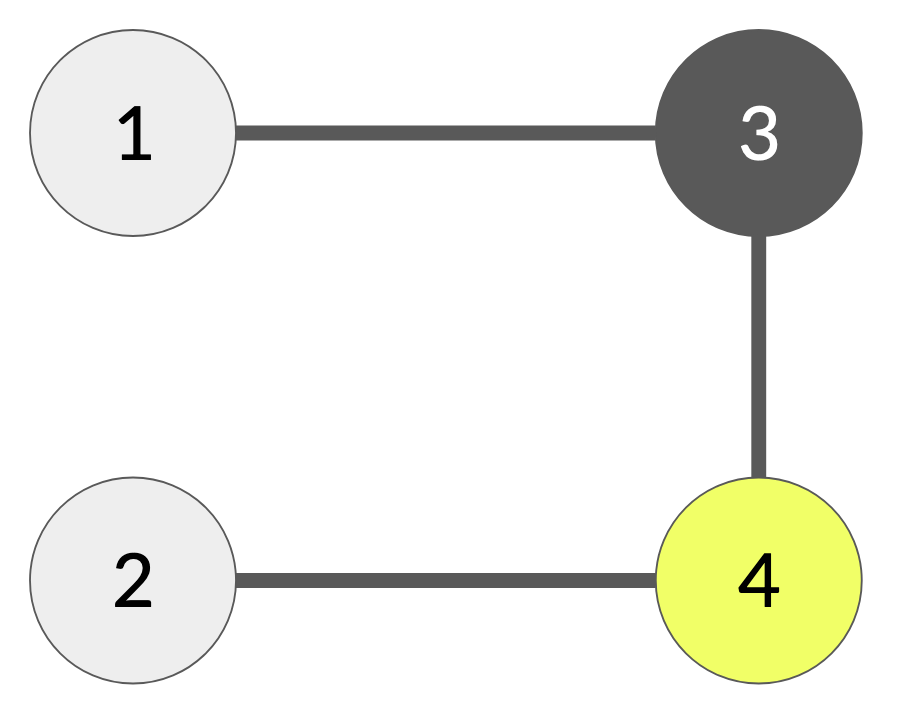
Proof. 실제 예를 보여봅시다. $V = {1, 2, 3, 4}, E = {{1,3}, {3, 4}, {4, 2}}$인 간단한 그래프입니다. 이 그래프는 $2$가지 색으로 채색을 할 수 있으며, 방법은 왼쪽과 같습니다. 하지만 그리디 색칠 알고리즘을 활용하면 오른쪽과 같이 $3$가지 색이 필요하게 됩니다. $\square$

최소 색을 사용하는 그래프 색칠	그리디 알고리즘의 그래프 색칠

그리디한 색칠이 항상 유용하게 사용될 수 있는 것은 아닌 것 같습니다. 하지만 원소들의 순서 $v_1, v_2, \cdots, v_{\lvert V \rvert}$ 을 적당히 정하면 색칠을 좀 더 잘 할 수 있을까요? 있을까요? 다음과 같은 분야에서 그리디한 색칠은 유용하게 사용가능합니다. 평면그래프를 색칠하는데 $6$가지 색이면 충분하다는 증명을 해 봅시다.

그리디 색칠

일단, $v_1, \cdots, v_{\lvert V \rvert}$ 를 어떤 순서로 고르면 될지 생각해봅시다. $v_i$를 고를 때는 $v_1, \cdots, v_{i-1}$ 의 색칠만 보기 때문에, 다음과 $(\Delta+1)$ 색 정리를 다음과 같이 쓸 수 있습니다.

Claim. 간선의 나열 $v_1, \cdots, v_{\lvert V \rvert}$와 정수 $D$가 존재해서, $\delta_{G[v_1, \cdots, v_{i-1}]}(v_i) \le D$인 경우, $\chi(G) \le D+1$입니다.

Proof. $v_i$ 를 칠할 때, $D$개 이하의 정수만 피하면 되기 때문에, 선택되는 수는 항상 $D+1$ 이하입니다. $\square$

이제 이 방식으로 적절히 간선을 고르는 방법을 살펴봅시다.

평면그래프

우리는 우선, 평면그래프를 정의합시다. 평면그래프란, 평면 위에 그래프를 그렸을 때, 간선들끼리 서로 교차하지 않도록 그릴 수 있는 그래프를 의미합니다. 이 때, 간선이 직선일 필요는 없습니다. 다음은 평면그래프와 평면그래프가 아닌 것의 예시입니다.

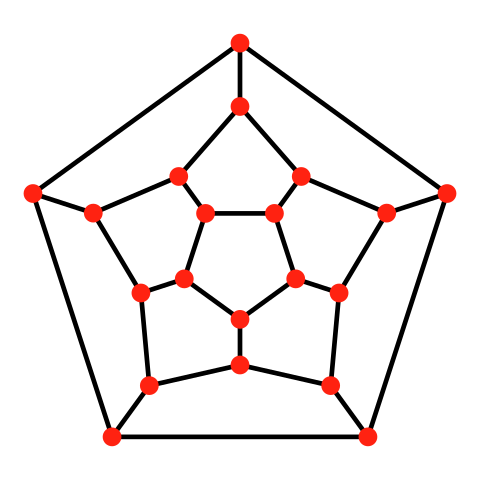
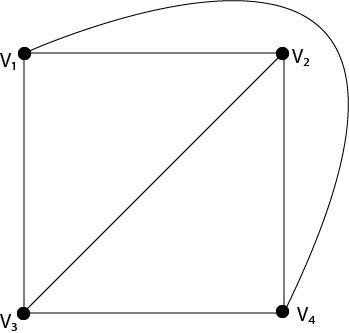
평면그래프의 예시	평면그래프가 아닌 두 그래프 $(K_{5}, K_{3, 3})$

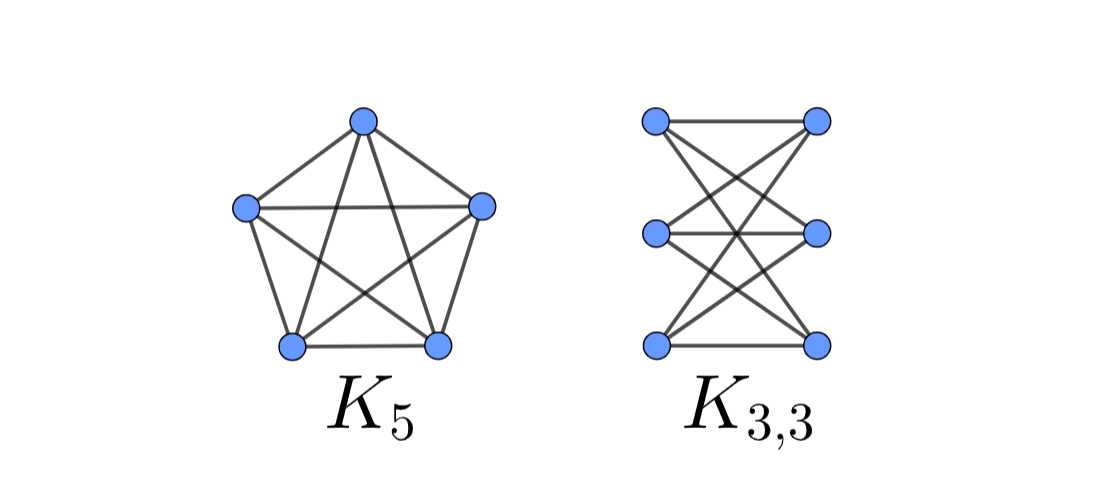이제, 평면그래프의 성질을 살펴봅시다. 평면 그래프에서 정점의 개수를 $v$, 간선의 개수를 $e$, 간선으로 나뉜 구역의 개수를 $f$ 라고 합시다. (가장 외부를 포함합니다)

• 첫 번째 그래프에서 $v = 20, e = 30, f = 12$이어서, $v-e+f = 2$ 입니다.
• 두 번째 그래프에서 $v = 4, e = 6, f = 4$이어서, $v-e+f =2$입니다.

이제 평면그래프에 대한 다음 성질을 증명합시다.

오일러 지표

Claim. 그래프의 $\chi = v-e+f$를 오일러 지표 (Euler Characteristic)라고 합니다. 연결된 평면그래프에서 $\chi = 2$ 입니다.

Proof. 가장 간단한 연결그래프는 정점 하나만 있는, $v = 1, e = 0, f = 1$ 인 경우고 $\chi =2$ 입니다. 이 그래프에 정점 혹은 간선을 하나씩 추가해봅시다.

• 연결 그래프를 만들기 위해 간선과 정점 하나를 추가한 경우 $v$와 $e$가 $1$씩 늘어나서 $\chi$ 가 유지됩니다.
• 두 정점 사이에 간선을 그을 경우, 하나였던 영역이 두 개로 나뉘면서, $e$와 $f$가 $1$씩 늘어나서 $\chi$ 가 유지됩니다. $\square$

더블 카운팅

더블 카운팅은 같은 대상을 두 가지 방법으로 세는 것을 의미합니다. 우리는 이 방법으로 간선의 개수를 $f$와 $v$의 기준으로 세어볼 것입니다.

Claim. 그래프의 각 영역이 $k_1, \cdots, k_f$ 개의 간선으로 둘러쌓여 있으면, $\sum_{i=1}^f k_i = 2e$ 입니다.

Proof. 각 영역에는 $k_i$ 개의 변이 있습니다. 하나의 변은 양쪽이 있고, 각 변은 정확히 두 개의 영역에 속하므로, $\sum k_i = 2e$입니다. $\square$

Claim. $\sum_{v \in V} \delta(v) = 2e$

Proof. 각 정점에는 $\delta(v)$ 개의 간선이 연결되어 있습니다. 하나의 간선은 양쪽 정점을 연결하기 때문에, $\sum_{v \in V} = 2e$입니다. $\square$

우리가 가지고 있는 도구를 활용해서, 최소 차수에 대한 성질을 증명합시다.

Claim. $v \ge 3$인 연결된 평면그래프에서 $e \le 3v-6$

Proof. 오일러 지표를 사용해서, $f = e-v+2$ 를 쓰면, $3(e-v+2) \le 2e$ 이고, $e \le 3v-6$ 입니다. $\square$

Claim. $v \ge 3$인 평면그래프에서 간선의 차수가 $5$ 이하인 간선이 존재합니다.

Proof. $\sum_{v \in V} \delta(v) \le 6v-12$ 이므로, 모든 $v$에 대해 $\delta(v) \ge 6$ 이면 $\sum_{v \in V} \delta(v) \ge 6v$ 여야해서, $\delta(v) \le 5$ 인 $v$가 존재해야합니다.

$6$색정리

Claim. $G$ 가 평면그래프이면 $\chi(G) \le 6$ 입니다.

Proof. $v \le 2$이면 자명하고, 연결그래프가 아닌 경우 각 연결성분에 대해 증명합니다. 이제, $v \ge 3$이고 연결그래프인 경우만 생각합시다. $G$에는 차수가 $5$ 이하인 정점 하나가 존재하므로, 해당 정점을 빼고 나머지를 $6$개 이하의 색으로 색칠합니다. 그 이후 해당 정점을 남는 색 하나로 색칠하면 됩니다. 그리디 알고리즘의 관점으로는 나열할 정점 $v_1, \cdots, v_{\lvert V \rvert}$ 를 역순으로 정해간다고 생각하면 됩니다. $\square$

이와 같은 방법으로, 정점의 차수를 제한하는 방식으로 문제를 해결할 수 있습니다.

연습문제

• NEERC 2010 K - K-Graph Oddity
• GCJ 2022 R3C - Mascot Maze

$4$색정리, Kempe Chain

평면그래프는 항상 $4$개의 색으로 칠할 수 있습니다. 이 증명은 1879년에 출시된 증명입니다. 이 증명을 유심히 살펴봅시다.

Claim. 평면 그래프는 $4$개의 색으로 칠할 수 있습니다.

Proof. 위에서 증명했듯, 평면그래프에는 차수가 $5$ 이하인 정점 $v$가 있습니다. 차수가 $3$ 이하인 점이 있으면 나머지 색으로 칠해주면 됩니다.

이제 차수가 $4$인 점이 있다고 생각합시다. 이 정점의 이웃에 사용된 색이 $4$개 이하이면 나머지 색으로 칠해주면 됩니다. 그렇지 않은 경우, 색이 연결된 시계방향으로 빨강, 노랑, 파랑, 초록이라고 합시다. 이제 정점에서 $v$와 노란색, 초록색 정점으로만 연결된 연결 성분을 생각해 봅시다. 이 두 색으로 연결된 연결 성분을 우리는 Kempe Chain 이라고 합니다. 이 Kempe Chain의 두 색은 마음대로 바꿀 수 있습니다. Kempe Chain 내부에서는 서로 번갈아가면서 색이 나타나기 때문에 상관 없고, 다른 연결된 정점은 두 색과 다른 색이기 때문에 상관 없습니다.

• 만약 이 Kempe Chain의 노란색과 초록색 정점이 ($v$를 거치지 않고) 연결되어있지 않은 경우, 초록색 정점에 연결된 Kempe Chain의 노란색과 초록색을 모두 바꾸어도 올바른 색칠입니다.
• Kempe Chain이 연결되어 있는 경우, 노란색 초록색 Kempe Chain을 바꾸는 것으로는 색이 다시 초록색, 노란색으로 바뀌어서 남는 색이 없게 됩니다. 이 때는, 파란색과 빨간색의 Kempe Chain을 확인하면 됩니다. 노란색과 초록색의 Kempe Chain이 파란색 정점과 빨간색 정점을 분리하게 되므로, 파란색과 빨간색의 Kempe Chain이 서로 연결되어 있을 수 없습니다. 이제 파란색 정점에 연결된 Kempe Chain의 색을 바꾸어서 올바른 색칠을 만들면 됩니다.

Kempe Chain이 연결되어있지 않은 경우	Kempe Chain이 연결된 경우

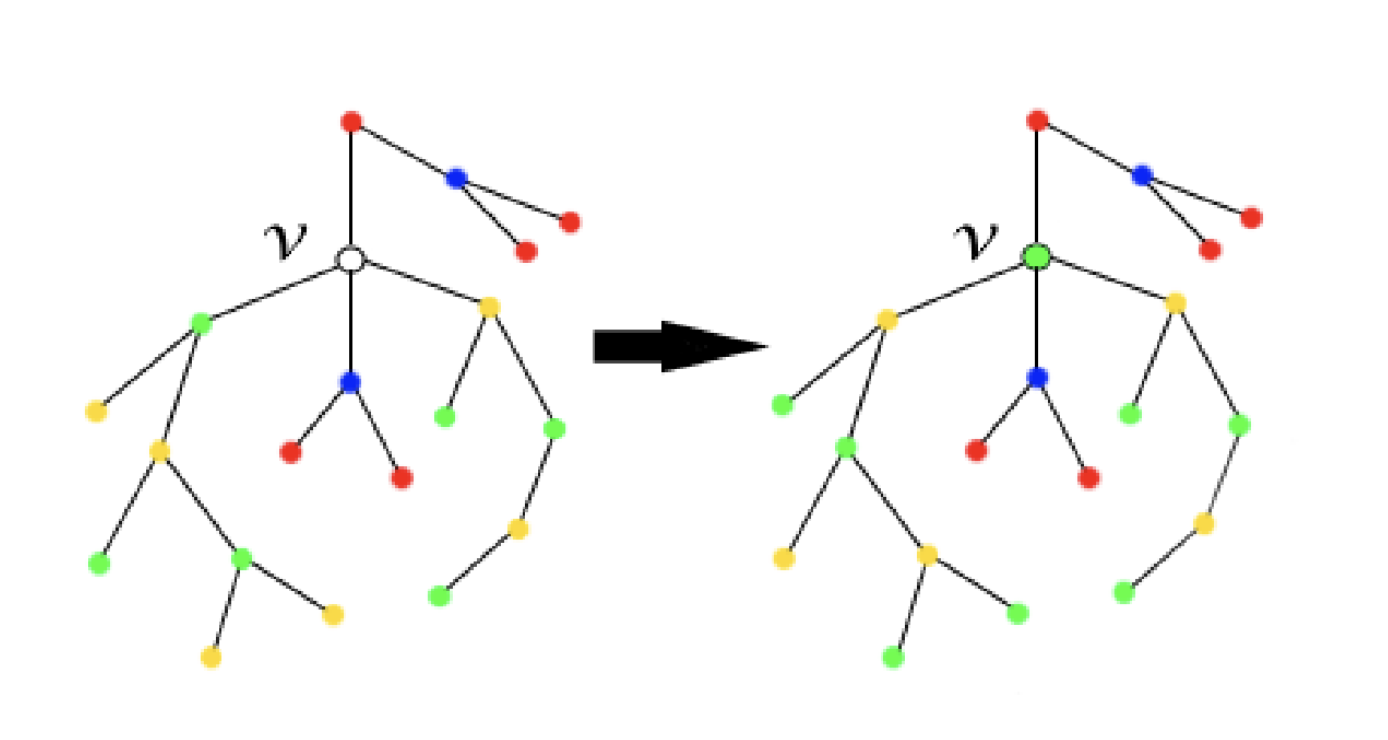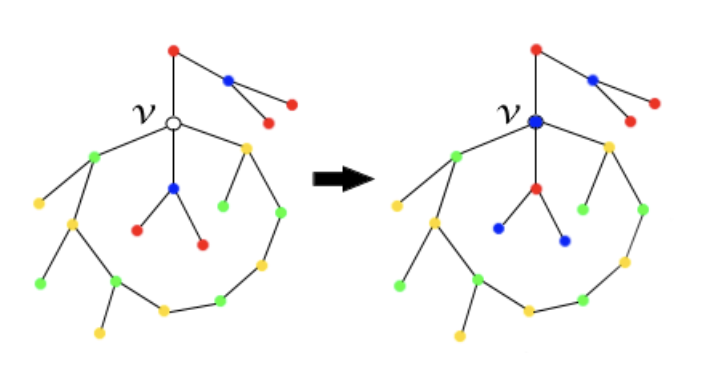이제, 차수가 $5$인 점이 있다고 생각합시다. $v$의 이웃에 $4$개의 색이 모두 사용되었다고 하면, 두 번 사용된 색이 있습니다. 두 번 사용된 색이 칠해진 정점이 인접할 경우, 두 정점을 합쳐서 하나의 색처럼 취급해서 $4$개의 색으로 칠하는 경우를 생각하면 됩니다.

이제, 두 번 사용된 색이 칠해진 정점이 인접하지 않은 경우를 생각해봅시다. 해당 정점을 초록색, 둘 사이에 있는 정점을 파란색이라고 합시다. 나머지 두 색을 노란색과 빨강색이라고 합시다. 즉, 시계방향으로 초록색, 파란색, 초록색, 노란색, 빨간색 순으로 칠해졌습니다. 파란색과 빨강색의 Kempe Chain 혹은 파란색과 노란색의 Kempe Chain 이 연결되지 않은 경우, 해당 색을 다시 칠해주면 됩니다.

그렇지 않은 경우, 초록색과 노란색의 Kempe Chain과 초록색 빨간색의 Kempe Chain은 연결되어있지 않습니다. 초록색쪽에서 두 Kempe Chain의 색을 바꿔주면 됩니다. $\square$

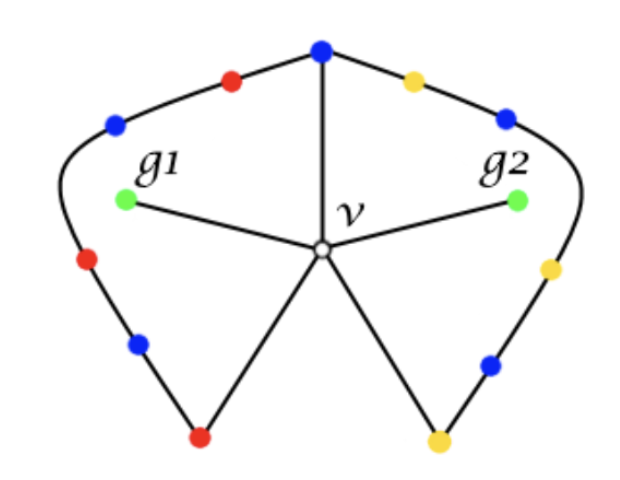
$5$색정리

사실 이 증명은 잘못되었습니다. 사실 증명이 매우 그럴싸해서 11년동안이나 사람들은 잘못된 부분을 찾지 못했습니다.

잘못된 부분은, Kempe Chain 두 개를 바꿀 때 색이 올바르게 바뀌는지는 모르기 때문입니다. 다음과 같은 반례가 있습니다.

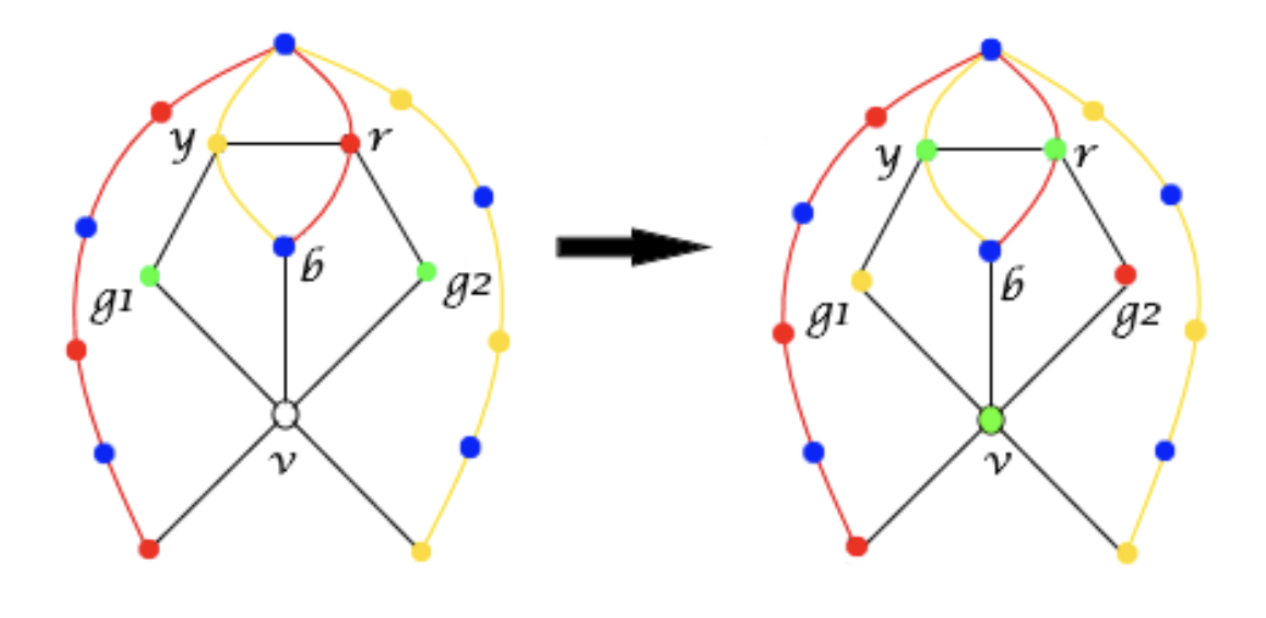
Kempe는 결국 이 문제를 해결하지 못했습니다. 그래서, 이 경우를 제외하고 증명이 가능한 $5$색 정리가 증명되었습니다. $4$색정리는 이후 1976년도에 증명되었으며, 컴퓨터를 사용한 최초의 증명으로 유명합니다. Kempe가 비롯 잘못된 증명을 했더라도, 아이디어인 Kempe Chain은 널리 쓰이고 있습니다.

연습문제

Kempe Chain의 개념을 사용해서 풀 수 있습니다.

• Asia Yokohama Regional 2018H - Four-Coloring

$\Delta$색정리

이제 $\Delta$색정리 ($\Delta$-Coloring Theorem, Brook’s Theorem)을 살펴봅시다.

Claim. 연결그래프 $G$가 홀수 사이클이나, 크기 $\Delta+1$의 완전그래프가 아닌 경우 $\chi(G) \le \Delta(G)$이다.

Proof. $\Delta = 2$ 인 경우 그래프가 홀수 사이클이 아니면 짝수 사이클이거나 경로이므로 $2$가지 색으로 칠할 수 있습니다.

이제 $\Delta=3$ 인 경우를 생각하고, 한 경우씩 제거해나갑시다.

• A. $G$의 모든 정점의 차수가 $\Delta$인 경우만 생각해도 됩니다. 그렇지 않을 경우, $\Delta$ 미만의 정점을 나머지 색으로 칠하면 됩니다.

이제 $G$의 한 정점 $v$를 잡고 인접한 정점 $v_1, \cdots, v_\Delta$ 가 일반성을 잃지 않고 각각 $1, \cdots, \Delta$ 색으로 칠해져있다고 가정합시다. 이제, $v$에서 $v_i$ 를 포함한 $i$와 $j$색으로 이루어진 Kempe Chain을 $C_{i, j}$라고 합시다.

• B. $C_{i, j} = C_{j, i}$ 인 경우만 생각하면 됩니다. 아닐 경우, $C_{i, j}$는 $v_j$ 를 포함하지 않으므로 $C_{i, j}$의 $i$와 $j$를 뒤집으면 됩니다.
• C. $C_{i, j}$가 $v_i$와 $v_j$를 잇는 경로인 경우만 생각하면 됩니다. 아닐 경우, $C_{i, j}$는 차수 $3$ 이상인 정점을 포함하고 있고, 이 정점과 정점 이웃은, $i$, $j$, 나머지 $\Delta-3$ 개 이하의 색으로 칠해져있습니다. 나머지 하나의 색으로 이 정점을 칠하면 $C_{i, j}$가 끊어지게 되어서 B번 조건을 만족하지 않습니다.
• D. $C_{i, j} \cap C_{i, k} = {v_i}$ 인 경우만 생각하면 됩니다. 아닌 경우, $u$는 정점 이웃 중 $i$를 $2$개, $j$를 $2$개 가지게 되고, 나머지 $\Delta-4$개 이하의 색을 씁니다. $i, j, k$가 아닌 나머지 하나의 색으로 이 정점을 칠하게 되면 $C_{i,j }$가 끊어지게 되어서 B번 조건을 만족하지 않습니다.

이제 이 경우에 색을 새로 칠해봅시다.

서로 인접하지 않은 $v_i$와 $v_j$는, $G$가 크기 $\Delta+1$의 완전그래프가 아니기 때문에 항상 존재합니다. 일반성을 잃지 않고 $v_1, v_2$라고 합시다. 그리고 $v_1 - u - \cdots - v_2$ 와 같이 경로가 구성되어있다고 합시다. 이제 $C_{1, 3}$의 $1$과 $3$을 뒤집읍시다. 뒤집은 이후 Kempe Chain과 $i$번째 색으로 칠해진 이웃을 $C^{\prime}_{i, j}$ 와 $v^{\prime}_{i, j}$ 로 표현합시다. $u$는 $2$번 색을 사용하고 있기 때문에, $v_1 = v^{\prime}_3$과 이어져있고, $u \in C^{\prime}_{2, 3}$ 입니다. D번 조건에 의해 $C_{1, 2}$는 $v_1$에서만 바뀌었기 때문에, $v$만 제거되었고, $u \in C^{\prime}_{1, 2}$ 입니다. 이제, $u \in C^{\prime}_{1, 2} \cap C^{\prime}_{2, 3}$ 이기 때문에 새로운 그래프는 D번 조건을 만족하지 않습니다. $\square$

채색다항식

이제 그래프 색칠에 대한 채색다항식(Chromatic Polynomial)에 대해 알아봅시다. 그래프 $G$를 $k$가지 색으로 칠하는 경우의 수를 $\pi_G(k)$라고 표현합시다. 기본적으로 채색다항식은 칠할 수 있는 색의 개수를 세어서 만들어집니다. 예를 들면, $v=5$인 간선이 없는 그래프는 각 색을 $5$가지 색으로 독립적으로 칠할 수 있으므로, $\pi_G(k) = k^5$입니다. $v=5$인 완전 그래프는 한 정점을 $k$ 색으로 칠하면, 다른 정점은 칠할 수 있는 색 하나가 줄어드므로 $k-1$가지 색… 이렇게 반복해서 칠해서 $\pi_G(k) = k(k-1)(k-2)(k-3)(k-4)$ 입니다. $v=5$인 트리는 루트를 $k$가지 색, 나머지를 부모 색을 피해야하므로 $\pi_G(k) = k(k-1)^4$입니다.

이제, 길이 $5$짜리 사이클을 봅시다. $1$번 정점을 $k$가지 색, $2, 3, 4$번 정점을 $k-1$가지 색으로 칠 할 수 있는데, $5$번 정점은 $1$번 정점과 $4$번 정점의 색이 다르면 $k-2$가지, 같으면 $k-1$가지로 칠할 수 있으므로, $1$번과 $4$번 정점의 색에 대한 정보를 추가로 알아야 $\pi_G(k)$ 를 구할 수 있습니다.

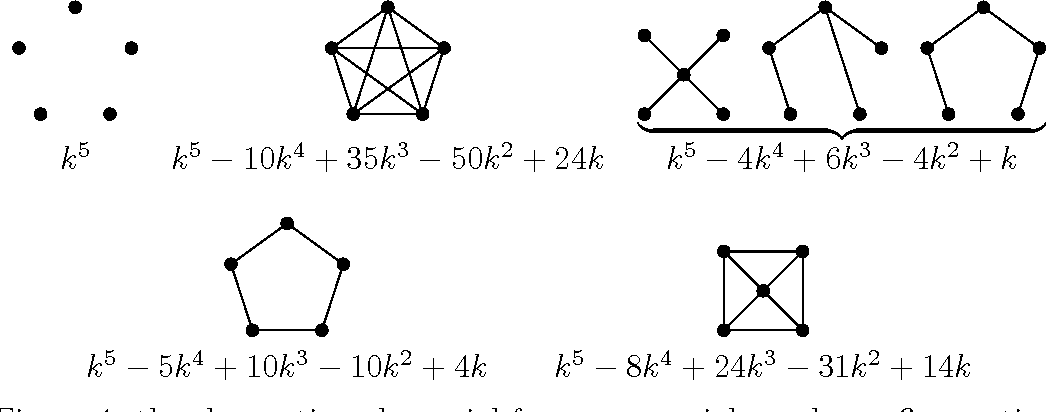
이런 경우를 어떻게 해결할까요, 또, $\pi_G(k)$는 이름처럼 항상 다항식이 맞을까요? 이를 위해서 다음과 같은 용어를 정의합시다.

• 그래프 $G$에서 $e$를 삭제한 그래프를 $G\setminus e$라고 표현합시다. $e$를 삭제(Deletion) 했다고 합니다.
• 그래프 $G$에서 $e = {v, w}$ 를 삭제한 이후에, $v$와 $w$를 붙인 그래프를 $G/e$ 라고 합시다. $e$를 축약(Contraction) 했다고 합니다.
  • 붙였다는 것은, $v$와 $w$를 $(v + w)$라는 새로운 정점으로 만들고, ${v, u}$ 혹은 ${w, u}$의 간선을 전부 ${(v + w), u}$로 바꾼 것을 말합니다.

이제 다음 사실을 증명합시다.

삭제-축약 정리

Claim. $\pi_G(k) = \pi_{G /e}(k) - \pi_{G \setminus e}(k)$

Proof. $G/e$의 채색 $f$를 생각해 봅시다. $e = {v, w}$라고 합시다.

• $f(v) \ne f(w)$ 인 경우 $f$는 $G$의 올바른 채색입니다.
• $f(v) = f(w)$ 인 경우 $f(v) = f(w) = f((v+w))$라고 하면, $f$는 $G \setminus e$의 올바른 채색입니다. $v$와 $w$가 같은 색으로 칠해졌고, $v, w$ 모두에 인접한 정점과 서로 다른색으로 칠해져있습니다.

그러므로 $\pi_{G/e}(k) = \pi_{G \setminus e}(k) + \pi_G(k)$입니다. $\square$

이제 $\pi_G$ 가 다항식인 것은, 간선이 없는 그래프 $G$의 $\pi_{G}(k) = k^{\lvert G \rvert}$이고, 다항식이 뺄셈에 대해 닫혀있다는 것을 이용해서, $\lvert V \rvert + \lvert E \rvert$ 에 대한 수학적 귀납법을 이용하면 증명할 수 있습니다. $\square$

결론

이 게시글에서 이분 그래프 색칠, 그리디 색칠, Kempe Chain, 채색 다항식에 대해서 다뤄보았습니다. 해당 내용은 그래프 채색에 대해서 굉장히 넓은 주제이고 그래프 채색의 기초적인 부분들을 알 수 있기 때문에 그래프 채색에 대해서 간단히 알고 싶을 때 짚고 넘어가거나, 더 많은 내용을 배우기 위해 디딤돌로 사용했으면 좋겠습니다.

각주