VennTum's profile image

VennTum

July 23, 2023 08:00

Fine-Tuning can Distort Pretrained Features and Underperform Out-of-Distribution (ICLR 2022 Oral)

AI , deep-learning

Fine-Tuning can Distort Pretrained Features and Underperform Out-of-Distribution

최근 들어서 굉장히 많은 딥러닝 영역에서 대규모 pretrained model을 특정한 downstream task에 대해 fine-tuning 하는 방식으로 학습을 진행하는 경우가 많습니다. 이전에는 데이터 셋의 규모가 작고 지금과 같이 transformer 구조를 사용하지 않을 때에는 요즘과 같이 large pretrained model이 크게 유행하지 않았습니다. 이전에는 많은 경우에 ImageNet 정도 사이즈의 데이터 셋에서 학습한 pretraiend model의 parameter를 가져와서 이보다도 더 작은 downstream task로 fine-tuning 하였기에 특정 task들에 대해서는 transfer learning을 적용해도 성능이 향상되지 않은 경우들도 있었으며, 모델 구조 자체가 대규모 학습에 용이하지 않은 경우도 있었습니다.

그러나 현재에는 거의 모든 분야에서 transformer 구조가 굉장히 큰 확장성과 대규모 학습을 처리해도 성능이 떨어지지 않는다는 점, 그리고 대규모 학습을 진행한 경우, 웬만한 downstream task에 transfer learning을 적용하였을 때에 성능이 향상한다는 점들이 알려지며, 거의 모든 분야에서 large pretrained model을 사용하는 방식으로 변화하였습니다. 이로 인해 CLIP, BERT 등 다양한 pretrained model을 사용하는 것이 굉장히 유용하고 효율적으로 문제를 해결할 수 있게 됩니다.

그 결과, 최근 양상은 이러한 pretrained model을 어떻게하면 특정 downstream task에 잘 적용할 수 있는지에 대해 중점적으로 연구되고 있습니다. 이러한 대규모 학습이 필요한 모델들의 경우, 실제로 한 번 학습하는 것에 굉장히 오랜 자원들이 필요하기에, 한 번 잘 학습시켜놓고 이를 잘 적용시키는 방향으로 많은 부분이 연구되고 있습니다. 실제로 제가 이전에 포스팅한 WiSE-FT의 경우도 이러한 large pretrained model을 downstream task에 적용하는 과정에서 fine-tuning을 한 이후 target distribution과 distribution shift case에 대한 두 가지 성능을 모두 끌어올리는 새로운 방법을 제안하기도 했습니다.

이번에 소개할 논문인 Fine-Tuning can Distort Pretrained Features and Underperform Out-of-Distribution도 이러한 transfer learning을 진행하는 과정에서 어떻게 더 효율적으로 성능을 끌어올릴 수 있는지에 대해 연구하였습니다. 그러나 이번 논문에서는 target이 완전히 large pretrained model에만 국한된 것은 아니며, 아예 transfer learning 자체를 효율적으로 할 수 있는 방법을 제안합니다.

해당 논문에서 소개하는 방법론은 어렵지 않으면서도 transfer learning이 진행되는 과정과 이를 통해 발생하는 문제를 해결하는 과정을 굉장히 잘 visualize하고, 이를 바탕으로 굉장히 쉽고 효율적으로 transfer learning을 진행하는 방법을 제안합니다. Transfer learning이 필요한 영역에서 누구나 쉽게 아주 약간의 코드 수정만을 통해 해당 기법을 적용할 수 있습니다. 이 논문은 이러한 점에서 참신함과 효율을 인정받아 ICLR 2022에서 Oral presentation을 진행할 수 있었습니다.

Introduction

Fine-tuning에는 크게 두 가지 방법이 있는 것이 잘 알려져있습니다. 실제로 지금 제가 fine-tuning이라고 두 개를 모두 통합하여 transfer learning 과정에서 pretrained model을 downstream task 데이터 셋에 대해 추가로 학습시키는 것을 이야기하고 있습니다. 그러나 실제로는 linear probing이라는 방법과 end-to-end fine-tuning이라는 서로 다른 fine-tuning 기법이 존재하며 이 둘이 보여주는 결과 양상도 상당히 다릅니다.

  • Linear probing: Pretrained model의 output 단에 레이어를 추가하여 downstream task를 위한 모델로 만든 이후, 기존의 pretrained model의 layer들은 모두 freeze하여 학습되지 않도록 한 이후, downstream task를 학습하면서 새롭게 추가한 output layer만 학습시키는 것
  • End-to-end fine-tuning: Linear probing과 동일한 모델 셋팅을 사용하나, 학습된 pretrain model layer들도 trainable하게 셋팅하여 downstream task를 추가로 학습하는 것

이 둘은 논문마다 명칭을 다르게 사용하기도 합니다만, 본 포스트에서는 각각 linear probing과 fine-tuning이라는 명칭을 사용해서 부르도록 하겠습니다. (실제로 WiSE-FT 논문에서는 이 둘을 linear classifier와 end-to-end로 구분하여 불렀습니다)

이 둘이 차별 양상을 보이는 가장 큰 부분은 바로 downstream task에 대해 학습했을 때의 성능과 distribution shift dataset에 대한 성능입니다. 보편적으로 알려져있는 결과는 fine-tuning의 경우, 해당하는 target distribution과 이와 유시한 small distribution shift들에 대해서는 linear probing보다 높은 성능을 보여준다는 것이고, 반대로 linear probing의 경우 down stream task의 target distribution과 상당히 먼 large distribution shift들에 대해서 fine-tuning에 비해 높은 성능을 보인다는 것입니다.

즉, linear probing은 OOD case에 대해 robustness를 잘 가지고 있으며, fine-tuning은 ID case에 대해 높은 성능을 보여줍니다. 이는 실제 해당 논문에서 실험하는 데이터 셋들 뿐만아니라, 많은 경우에도 이러한 양상을 잘 보여줍니다. 실제로 저번에 포스팅한 WiSE-FT에서도 linear probing의 경우 ImageNet을 target distribution으로 했을 때, 이와 유사한 ImageNetV2 등에 대해서는 fine-tuning보다 낮은 성능을 보였으나, distribution shift가 강한 ObjectNet, IN-A 등에 대해서는 fine-tuning보다 월등한 성능을 보였습니다.

이에 해당 논문에서는 이렇게 linear probing과 fine-tuning이 distribution shift case에 대해서 성능 차이가 나는 이유에 대해 분석하고, 이를 개선하여 fine-tuning과 linear probing의 장점을 합한 새로운 fine-tuning 기법인 LP-FT를 제안합니다.

Theory

Linear overparameterized setting

저자들은 어떠한 condition에서 fine-tuning이 linear probing보다 OOD에 약한지 확인하기 위해 pretrained feature가 해당 target에 대해 좋은 성능을 보이며, 이에 대한 OOD shift가 큰 linear setting에 대해 실험합니다.

이를 위해 특정 데이터 셋에 대해 L2 norm loss를 사용하는 regression case를 테스트합니다.

위 상황을 해결하는 모델의 feature extractor를 B, B’ 이라 할 때, 해당 feature extractor들 사이의 distance는 다음과 같이 정의됩니다.

  • Feature Extractor Distance: $d(B, B’) = min_{U}   B - UB’   _{2}, where U is rotation matrix, B, B’ are orthonormal$

이와 같이 정의된 feature extractor distance에 대해, 좋은 성능을 보이는 Good pretrained feature $B{0}는 특정한 오차 \epsilon과 optimal feature extractor $B^{}$에 대해 $d(B{0}, B^{} <= \epsilon$인 경우를 이야기합니다.

이러한 상황에서, 해당 distribution들에서 유용한 feature set을 공유하고 있는 ID와 OOD가 존재한다고 할 때, pretrained model이 학습 과정에서 해당하는 large dataset에 대해 학습하는 과정에서 각각의 downstream task의 ID와 OOD에 대한 unlabeled 혹은 weak supervised learning이 되었을 경우, $B_{0}가 B^{*}$와 가깝다고 가정할 수 있도록 학습된 상황이 일어날 수 있습니다.

저자들은 이러한 B0가 존재하는 상황에서도, fine-tuning이 이를 distort하여 낮은 OOD accuracy를 만들 수 있다는 것을 증명합니다.

이외에 더 자세한 세팅 디테일에 대해서는 논문에서 확인하실 수 있습니다.

이제 실제로 이러한 상황 속에서 어떠한 결과를 저자들이 확인하였는지 살펴보도록 하겠습니다.

저자들은 위와 같은 configuration 속에서, 각각의 pretrained feature extractor들을 해당하는 ID에 대해 linear probing(LP)와 fine-tuning(FT)를 사용하여 학습합니다. 그리고 이와 같이 학습된 각각의 feature extractor가 실제 ID와 OOD에 대해 어떠한 성능을 갖는지 확인하였습니다.

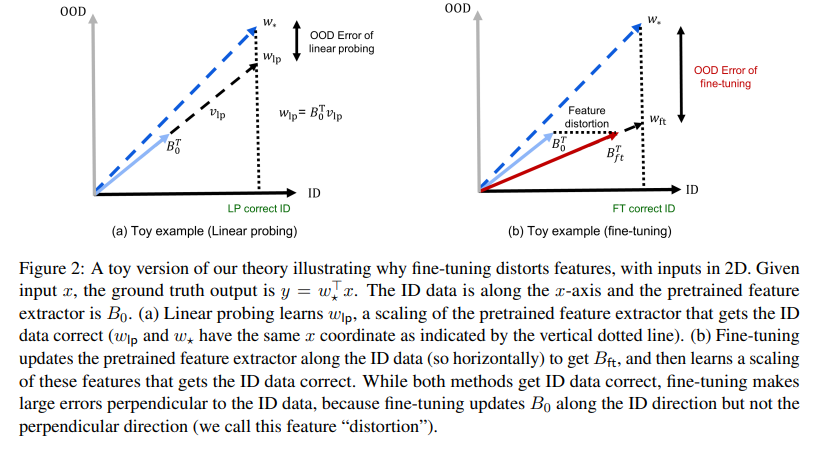
위 그래프가 앞서 이야기한 linear overparameterized setting에 해당하는 toy example 결과 그래프입니다. 이 때, 앞선 feature extractor를 B, 그리고 해당 downstream task를 풀기 위한 head parameter를 v라고 했을 때, 실제 모델의 전체 parameter는 $w=Bv$ 꼴로 나타나게 됩니다. 그리고 실제 ground truth에 해당하는 optimal w를 $w_{*}$라고 했을 때 위와 같은 양상의 그래프 결과가 나오게 됩니다.

여기에서 확인할 수 있는 점들은 다음과 같습니다.

먼저 linear probing의 경우, pretrained feature extractor B0에 맞춰서 해당하는 head parameter v를 학습하여 $w_{lp}$를 학습하여 만들어냅니다. 이 결과로 기존의 pretrain feature extractor는 해당하는 dataset에 대해 ID인지 OOD인지 여부에 영향받지 않고 각각의 dataset에 대한 정보를 약하게나마 학습한 상태이기 때문에, 해당 B0는 실제 optimal인 $w_{*}$와 OOD accuracy 측면에서 가깝게 align되어 있습니다. 이에 대한 feature extractor 부분은 freeze한 상태로 head parameter만 학습하게 되기 때문에, 그 결과로 생기는 linear probing의 경우 OOD error 측면에서 optimal과 큰 차이가 나지 않습니다.

그러나 이는 fine-tuning에서는 다른 양상을 보이게 됩니다. fine-tuning의 경우 학습 과정에서 feature extractor를 포함한 모든 layer들이 영향을 받고 변화하기 때문에, ID 데이터에 맞추어 fine-tuning하는 과정에서 feature extractor도 ID correction을 높이는 방향으로 변화하게 됩니다. 그 결과로 실제로 OOD와 ID를 모두 고려한 때의 optimal과는 꽤나 각도, 거리가 멀어지게 되며 이 결과 해당 경우의 OOD error는 굉장히 커지게 됩니다.

이러한 현상 속에서, 저자들은 이렇게 fine-tuning 과정에서 feature extractor가 ID direction에 맞추어 update되며 기존의 feature extractor에서 변화하고 ID에 수직으로 큰 오류를 만들어내는 현상을 ‘distortion’이라 정의합니다.

저자들은 이러한 ft에서의 distortion이 일어날 때, 학습 특정 step t에서의 OOD error lower bound에 대해 다음과 같은 식을 유도해냈습니다.

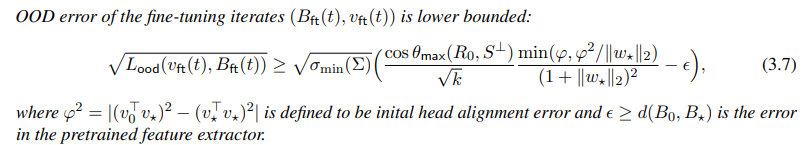이를 유도하는 자세한 과정은 논문에서 확인하실 수 있습니다.

여기에서 중요하게 보셔야할 점은, 이러한 lower bound를 구한 결과값에 영향을 주는 요소로 initial head alignment error와 pretrained feature extractor error가 요소로 들어가있다는 것입니다. 여기에서 pretrained feature extractor에 대해서는 우리가 좋은 데이터 셋에 대해 잘 학습하는 것 이외에는 건드릴 수 있는 부분은 없습니다.

그렇다면 우리가 해당 lower bound를 더 줄일 수 있는 부분은 어떤 부분을 수정하는 것일까요? 이에 대한 고려가 바로 LP-FT의 핵심이며, 해당 이야기가 이후에 나올 예정입니다.

LP vs FT

위 결과를 통해서 fine-tuning을 하는 경우, distortion을 만들어내기 때문에 실제로 학습 과정에서 OOD에 대한 accuracy가 optimal과 큰 격차를 만들어낸다는 것을 확인할 수 있었습니다. 그러나 이러한 결과가 꼭 linear probing이 더 낫다는 것을 의미하지는 않습니다. 그 이유는 linear probing이 OOD 관점에서는 더 우수하지만, 다음과 같은 상황에서 ID accuracy가 더 낮기 때문입니다.

  • ID distribution이 lower dimension subspace에 대해 density가 있을 때
  • B0가 B*에 가까울 때(즉, 좋은 pretrained feature extractor를 가지고 있을 때)

여기에서 이야기하는 첫 번째 조건은 ID data가 전체 dimension이 d, feature dimension이 k라고 하였을 때, 해당 dataset이 k < m < d-k인 m-dimenstional subspace S에 lying on되어있으며 전체 trainig example n이 m보다 클 때의 경우를 이야기합니다.

반면 OOD에 대해서는 해당하는 subspace S가 B*의 rowspace에 직교하지 않는 한, linear probing이 fine-tuning보다 더 좋은 성능을 갖게 됩니다.

Extension - Linear probing then fine-tuning: a simple variant to mitigate tradeoffs

앞서 확인한 바들을 따르면, fine-tuning의 장점은 feature extractor와 head가 모두 downstream task에 대해 fit할 수 있다는 것입니다. 이에 저자들은 좋은 pretrained feature를 가지고 있을 때, 이러한 benefit을 그대로 유지하면서 OOD error를 더 낮출 방법을 생각했습니다.

앞서 OOD error lower bound에 대해 이야기할 때, 분자에 initial head alignment error가 중요한 영향을 미치고 있음을 이야기한 적이 있습니다. 지금 현재 가지고 있는 이슈는 FT를 하는 과정에서 head가 random initialization되고 있어서, 해당 error가 보통 굉장히 크다는 것입니다. 그 결과 fine-tuning을 할 때에는 feature extractor와 head가 같이 coupled된 상태로 update되기 때문에, head가 크게 변화하며 fitting되는 과정에서 feature extractor도 distorted하며, OOD error가 커지는 문제가 발생합니다.

이를 해결하기 위해서 우리는 better head initialization이 필요함을 알 수 있습니다. 그리고 저자들은 여기에서 굉장히 좋은 head initializing을 다음에서 발견합니다. 바로 ‘linear probing’입니다.

Linear probing을 통해 얻은 head는 실제 optimal에 해당하는 v*와 굉장히 가깝게 align되어 있습니다. 이러한 head를 사용하면 실제 학습 과정에서 head의 변동성이 크지 않기 때문에, feature extractor의 distortion도 더욱 작아질 수 있고 OOD error를 낮추는 역할을 할 수 있습니다.

이는 실제 식을 통해서도 구해줄 수 있습니다. 만약 우리가 perfect feature extractor B를 가지고 있을 경우, v0가 최적화된 linear probing head $v_{lp}^{\infty}$를 가지게 된다면, 이로 인해 발생하는 feature extractor error와 head initialization error 모두 0이 되어 ft를 통한 OOD error가 모든 step에 대해 0의 lower bound를 가질 수 있게 됩니다.

해당하는 case를 고려하는 것은 이상적인 상황에서 고려된 것이기 때문에, 우리가 perfect feature extractor를 가지고 있지 않을 때와, 무한 step의 linear probing을 진행하지 않은 상태의 linear probing을 사용하였을 때를 analyze하기는 어렵습니다. 그러나 이를 통해서 lower bound가 줄어든다는 것을 확인했기 때문에, 저자들은 다음과 같은 방법을 제안하고 실제 실험을 통해 결과 향상을 확인합니다.

  • pretrained feature extractor를 freeze하고 head만 학습하는 linear probing을 몇 step 진행한다.
  • 이후 freeze를 푼 이후 feature extractor와 head를 같이 학습하는 fine-tuning을 진행한다.

해당 방법이 바로 저자들이 새롭게 제시하는 fine-tuning 기법, LP-FT입니다.

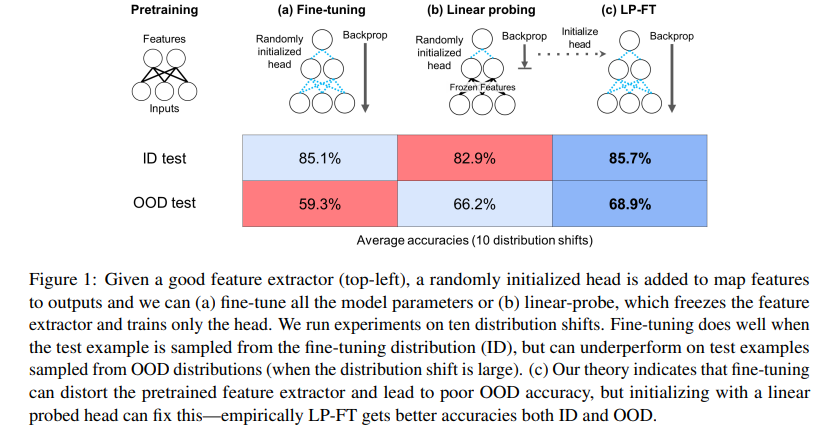
Experiments

저자들은 여러 dataset에 대해 실제 LP-FT가 성능을 향상시킬 수 있는지 실험합니다.

이를 위해 사용한 데이터 셋들은 다음과 같습니다.

  • DomainNet
  • Living-17 and Entity-30
  • FMoW Geo-shift
  • CIFAR-10 → STL
  • CIFAR-10 → CIFAR-10.1
  • ImageNet-1K → ImageNetV2, ImageNet-R, ImageNet-A, ImageNet-Sketch

이에 실제로 적용할 pretrained model들은 다음과 같습니다.

  • CLIP pretrained ViT-B/16 for ImageNet

이외에도 resnet-50을 사용한 데이터 셋 및 결과, 자세한 세팅 등은 appendix에서 확인하실 수 있습니다.

실제 LP-FT 실험 결과는 다음과 같습니다.

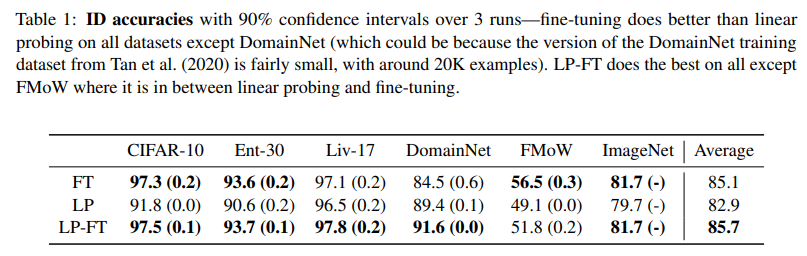
먼저 각각의 downstream task로의 fine-tuning한 모델들의 ID accuracy입니다.

여기서 확인할 수 있는 것은 거의 모든 경우에서 LP-FT를 사용했을 때에 ID accuracy가 더 높게 나왔다는 것입니다. 그러나 주의해야할 점은 해당 dataset들 중 이러한 양상이 나온 경우는 바로 linear probing과 fine-tuning, LP-FT의 accuracy가 항상 앞선 분석과 같은 경향성을 보이지는 않았다는 것입니다.

예를 들어, DomainNet의 경우에는 linear probing이 fine-tuning보다 오히려 좋은 ID performance를 보였습니다. 그리고 FMoW의 경우에는 fine-tuning이 LP-FT보다도 더 좋은 성능을 보였습니다.

이러한 case들이 발생하는 경우를 고려하여 선택할 필요가 있습니다.

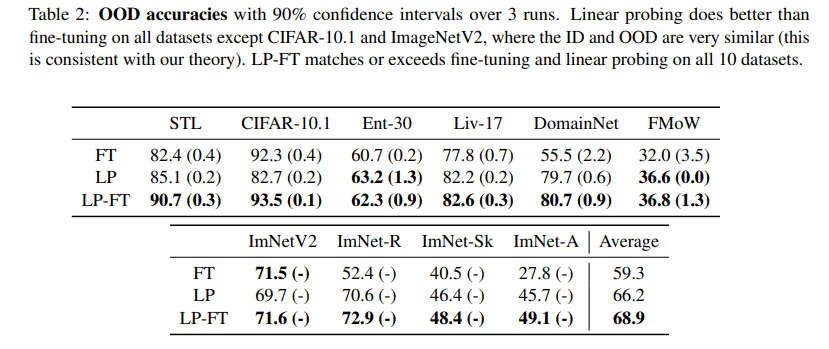
다음은 OOD accuracy table입니다. 여기에서 확인할 수 있는 점은 모든 경우에서 LP-FT가 fine-tuning과 linear probing보다 더 좋은 OOD accuracy를 보였습니다.

다만 여기에서도 주요하게 보아야할 점은 ImageNetV2, CiFAR-10.1 같은 경우에는 fine-tuning이 linear probing보다 더 높은 OOD accuracy를 보였습니다. 그 이유는 이전에 WiSE-FT에서도 이야기한 적 있듯, ID dataset과 OOD dataset 사이의 distribution shift 정도가 얼마나 되어있냐에 따라서 fine-tuning을 했을 때에 OOD robustness를 잃어버리는 정도와 ID accuracy가 증가하는 정도에 영향을 받기 때문임을 실험적으로 확인할 수 있었습니다.

그러나 좋은 점은 LP-FT의 경우 나머지 두 기법보다 항상 더 좋은 OOD accuracy를 보였습니다.

Conclusion & Discussion

이제 해당 LP-FT 논문에서 더 이야기된 나머지 논의점 및 정리에 대해서 더 이야기하고 마치도록 하겠습니다.

저자들은 해당 논문에서 여러가지를 발견하고 이에 대한 논의를 제안해두었습니다.

첫 번째 논의는 상당히 흥미롭습니다. 이는 바로 fine-tuning에서 early stopping이 feature extractor의 distortion을 완화하지 않는다는 점입니다. 단순하게 생각하면 fine-tunign의 distortion은 train을 거듭하는 과정에서 ID쪽에 더 가깝게 align 되어가는 과정처럼 생각할 수 있습니다. 이에 거듭할수록 distortion이 발생하고 과적합되기 때문에 early stopping을 하면 해당 distortion을 완화할 수 있을지 저자들은 직접 체크해보았습니다. 그 결과, fine-tuning에서 여러 셋팅을 사용하여 early stopping을 적용하더라도, distortion 문제 자체가 해결되지는 않으며 OOD accuracy는 linear probing이 더 낫다는 것을 발견합니다.

두 번째로는 ID-OOD feature는 fine-tuning 과정에서 distortion이 발생한다는 것입니다. 실제로 LP-FT를 사용했을 때에 ID example들의 average distance는 fine-tuning에 비해 20배 작다는 것을 확인합니다.ㅣ

세 번째로는 pretrained features들은 잘 학습되어있어야 하며, ID와 OOD 사이의 distribution이 크게 다르고 거리가 멀어야 위와 같은 관찰 및 LP-FT의 효율이 극대화된다는 것입니다. 이는 앞서 제가 이야기한 부분과 유사하기도 합니다. 이러한 부분이 위반될 때에는 fine-tuning이 linear probing보다 더 좋은 성능을 보이게 됩니다.

위에서 이야기된 부분들을 모두 잘 고려하여, 어떠한 task에 대해서 fine-tuning을 진행할 것인지, linear probing을 진행할 것인지, 혹은 LP-FT를 사용할 것인지를 잘 판단하실 수 있으면 시간을 절약하고 성능을 끌어올리는 데에 긍정적인 영향을 줄 수 있다고 생각합니다. 제가 생각할 때에 해당 논문에서 좋은 점은 바로 fine-tuning 과정 자체에 대한 이해를 높여준다는 부분이 큰 것 같습니다. 보통 어떠한 경우, 어떠한 task에 무엇을 사용해야할지 감각을 잡기 어려울 수 있고, 그 특성에 대한 감을 익히는 것이 어려울 때가 많습니다. 본 논문은 fine-tuning과 linear probing의 성질을 이상적인 상황에서 이해하고 이를 수행하는 과정을 보여주었다는 점에서 한 번 즈음 읽어보시는 것을 추천합니다.