September 26, 2023 00:00

이 글에서는 현재 양자 인공신경망이 직면한 가장 큰 문제인 Barren Plateaus에 대해 다룬다. 이 현상은 큐비트가 늘어나면 gradient가 사라져서 학습이 불가능해지는 현상을 말한다.

본 글에서는 이 현상을 소개하고, 수학적으로 기술하고자 한다. 이때 논문 [2]의 내용을 참고하였다. 글의 말미에는 코드를 통해 이 현상이 실재함을 확인한다.

서론

앞으로 당분간의 양자컴퓨터 시대를 NISQ area라고 부르는데, 이 뜻은 적당한 큐빗 수(~1000개)이면서, 에러를 제거할 수 없는 양자컴퓨터를 말한다. 큐빗 수에 제한을 둔 이유는 큐빗 수가 엄청나게 많다면 이들을 사용해서 에러가 없는 큐빗을 만들 수 있기 때문이다. 결국 NISQ를 한 문장으로 요약하자면, 지금처럼 에러가 무시할 수 없는 수준인 적당한 큐빗을 가진 양자컴퓨터라고 할 수 있다.

IBM사는 433큐빗 양자컴퓨터를 개발하였고, IONQ사는 32큐빗 양자컴퓨터를 공개하였다. 두 회사의 큐빗 수가 10배 이상 차이나지만, 현재의 양자컴퓨터는 에러율이 중요하기 때문에 단순 비교는 불가능하다. 이 두 컴퓨터 모두 NISQ 시대의 대표적인 컴퓨터이다.

NISQ area에서 가장 유망한 분야는 Quantum Machine Learning(QML) 분야이다. QML하면 대표적인 것은 고전적으로 파라미터를 저장하고, 이 파라미터를 사용해 양자 회로를 조작하는 Parameterized Quantum Circuit이다. 보통 이 개념을 Quantum Neural Network(QNN) 이라고 부르기도 하는데, 고전적인 NN의 그것과 구조는 다르지만, 뭐 대충 목적과 방식이 비슷하니 Neural Network라고 부르는 듯 하다.

그런데 QNN에는 Barren Plateaus 라는 큰 한계점이 존재한다. 한국어로 번역하면 “불모의 고원” 이다. 이 개념은 양자 인공신경망에서 쌓을 수 있는 레이어와 사용할 수 있는 큐빗 개수에 한계가 존재한다는걸 시사한다. 큐빗수도 늘리고, 레이어도 많이 쌓아야 양자컴 쓰는 이유가 있는데, 그걸 못 한다니.. 아주 암울한 이야기이다. 지금부턴 Barren Plateaus가 무엇이며 왜 발생하는지를 소개하고자 한다.

Barren Plateaus란?

Barren Plateaus(BP)란 양자 인공신경망에서 파라미터의 gradient가 지수적으로 감소해서 종국엔 학습이 불가능해지는 현상이다.

BP는 인공신경망에서의 Gradient Vanishing과 유사한 문제이다. Gradient vanishing은 활성화 함수를 ReLU로 바꾸거나, Skip connection을 사용하거나, 기타 등등 많은 해결법이 나오면서 요즘에는 크게 문제가 되지 않는 수준이다.

하지만 Barren Plateaus는 일반적인 양자 인공신경망이라면 피해갈 수 없는 것처럼 보인다. 그 이유는 양자 정보에서 사용되는 개념인 측도 집약화 현상 때문이다.

측도 집약화란?

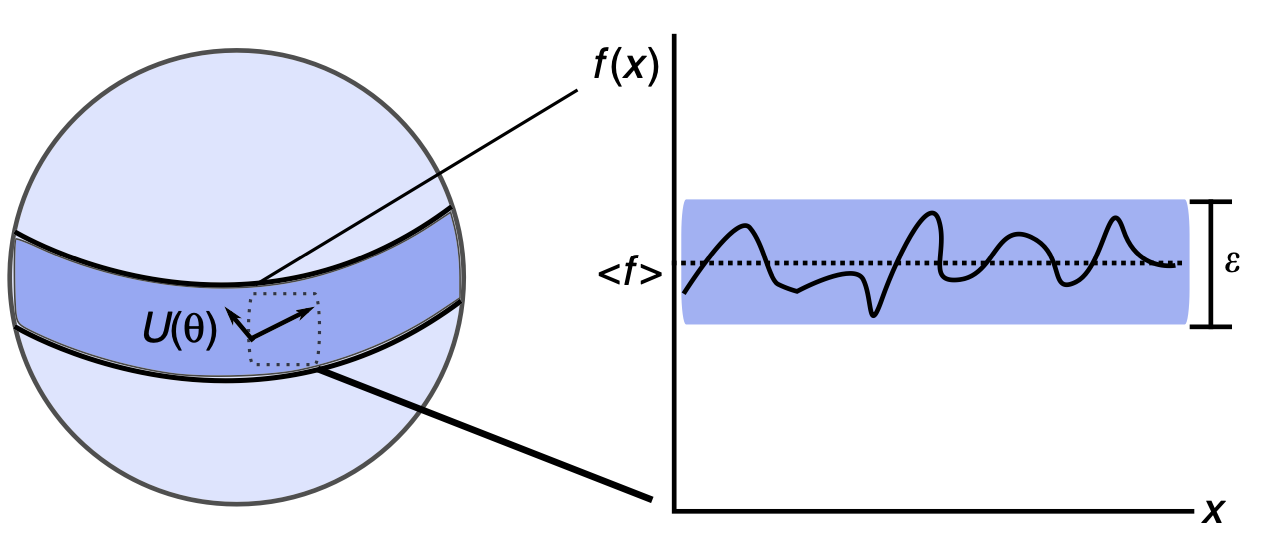
위 그림 1은 측도 집약화를 간략하게 보여주고 있다. 임의의 양자 상태는 행렬로 표현되고, 고윳값이 상태별로 확률값을 가지기 때문에 행렬의 trace값이 1을 만족한다. 따라서 양자 상태는 Hypersphere에 표현된다.

랜덤하게 양자 상태를 생성하면 그 값은 Hypersphere상의 적도에 존재할 확률이 아주 아주 크다(Levy’s lemma). 따라서 Hypersphere상에서 관측값을 구하면, 대부분의 값이 적도에 몰리는 현상이 발생하는데, 이 현상이 측도 집약화이다.

큐비트가 늘어나면서 hypersphere의 차원이 커지면 적도로부터 특정 각도 이상 차이날 확률이 지수적으로 작아진다. 결국 모든 양자 인공신경망은 관측값(Observable) 기반으로 gradient를 계산하는데, 관측값이 적도에서 유의미하게 멀어질 확률이 사라지면 gradient의 크기도 줄어든다. 앞으로 Barren Plateaus에 대해서 증명할 모든 내용은 사실상 이 직관으로부터 이해 가능하다.

Barren Plateaus의 수학적 증명

수학적인 증명을 통해 보이고자 하는 것은 두 가지이다.

1. gradient의 기댓값이 0이다.
2. gradient의 분산이 0에 가깝다.

(논문에서 사이 과정을 많이 생략해서 정리하는 과정이 쉽지 않았다..)

상황 세팅

앞으로 BP를 논할 양자 회로는 random parameterized quantum circuits (RPQC)이다. PQC까지는 알겠는데, Random parameterized 조건이 붙은 이유는, 앞으로 증명 과정에서 유니터리가 랜덤으로 정해짐을 가정하기 위해서이다. 만약 특정 분포 하에서의 유니터리만 사용한다면 BP가 발생하지 않을 수도 있다. 이에 대해선 마지막의 해결책 에서 다시 다룬다.

RPQC는 다음과 같이 정의된다.

여기서 $U_l$는 파라미터 $\theta_l$에 의해 조정되는 유니터리 연산자이며, $W_l$은 파라미터와 무관한 유니터리 연산자이다. 고전적인 신경망에서 activation function이라 생각하면 된다.

신경망에서 cost function이 주어지듯이, RPQC도 결국엔 최적화 하고자 하는 값이 존재한다. 이는 Observable의 형태로 다음과 같이 주어진다.

이제 k번째 파라미터 $\theta_k$에 대한 그래디언트 구하기 위해, 아래와 같이 정의하자.

$\theta_k$가 무작위로 초기화된 것이 가정이므로, $U_-$와 $U_+$는 독립임에 유의하자. 이제 k번째 파라미터 gradient을 아래의 식으로 얻을 수 있다. 증명은 꽤 복잡하므로 생략한다.

BP가 존재한다는 것을 보이기 위해선, $\partial_k E$값이 아주아주 작아진다는 것을 보이면 충분하다. 따라서 저 값의 (기대)평균과 (기대)분산을 계산할 것이다.

$\langle \partial_k E \rangle$ 계산

아래 식은 정의로부터 아주 명확하다.

$p(U)$는 유니터리 $U$의 확률분포 함수이다. $U$는 $U_-$와 $U_+$로 분해되므로, 둘의 확률로 분해하여 표현할 수 있다.

이 식을 첫 식에 대입하면 아래의 결과를 얻는다.

위 식에서는 $\rho = U_-\vert 0\rangle\langle0\vert U_-^\dagger$ 의 치환이 사용되었다. 또한 Trace연산자 안에서 순서를 자유자재로 바꾸었음에 유의하자.

이제 아래의 성질을 사용하고자 하는데, 이 식은 논문 [3]에서 증명되어 있다. 항상 성립하는 식은 아니고, $\mu(U)$가 Haar measure을 만족할 때 성립한다.

지금 증명에는 $O$가 굳이 행렬일 필요도 없다. $U$와 무관한 상수값 c라고 생각하면 당연히 아래의 식이 성립한다.

$U_-$와 $U_+$둘 중 하나는 반드시 1-design인데, t-design은 t차함수의 적분값을 유한한 대표값 몇개를 골라서 계산할 수 있게 해주는 편리한 방식이다. 여튼 $U_-$가 1-design인 경우엔 위 성질을 사용할 수 있고, 따라서 아래처럼 식이 정리된다.

마지막으로, Haar measure의 left, right invariant한 성질을 사용하자. 수식적으론 아래와 같이 표현되는 성질이다.

이 성질을 사용하면 $\langle \partial_kE\rangle$의 최종적인 값을 구할 수 있다.

만약 $U_+$가 1-design인 경우엔 $\langle \partial_kE\rangle=i\int dU_-p(U_-)\text{Tr}{\rho \int dU_+p(U_+)\left[V, U_+^\dagger H U_+ \right]$ 이 식에서부터 위의 성질을 사용할 수 있어서 0임이 쉽게 유도된다.

따라서 파라미터가 무작위로 초기화됨을 가정했을 때, 그 gradient $\partial_k E$의 기댓값 $\langle \partial_kE\rangle = 0$이다. 이제 분산이 아주 작아짐을 증명하러 가자.

$\text{Var}\left[\partial_k E\right]$ 계산

$\text{Var}\left[\partial_k E\right]$ 계산은 조금 더 복잡하나, 접근방식은 예상하기 쉽다.

이제 $\langle (\partial_kE)^2\rangle$를 구해야 한다.

이는 $U_+$, $U_-$에 대한 최대 2차식으로 표현되므로 2-design을 사용해야 한다. 이 경우엔 아래 3가지 경우 중 하나가 성립한다.

• $U_+$가 2-design
• $U_-$가 2-design
• 둘 다 2-design

각각의 경우에 대해 값을 따로따로 구해주어야 하는데, 이 과정은 너무 복잡하여 정리하기에 무리가 있다. 요약하자면 Haar measure상에서 2차식 적분값을 2-design으로 구하는 것이므로 단순 노가다이고, 논문 [3]에 잘 정리되어 있다.

결과만 정리하자면 다음과 같다.

• $U_+$가 2-design 인 경우: $\text{Var}[\partial_kE] \approx -\frac{\text{Tr}(\rho^2)}{2^{2n}-1}\text{Tr}\langle [V, u^\dagger H u] \rangle_{U_+}$
• $U_-$가 2-design 인 경우: $\text{Var}[\partial_kE] \approx -\frac{\text{Tr}(H^2)}{2^{2n}-1}\text{Tr}\langle [V, u\rho u^\dagger] \rangle_{U_-}$
• 둘 다 2-design 인 경우: $\text{Var}[\partial_kE] \approx \frac{1}{2^{3n-1}}\text{Tr}(H^2)\text{Tr}(\rho^2)\text{Tr}(V^2)$

위 식에서 제일 중요한 값은 큐빗 수를 나타내는 n이다. n이 커짐에 따라 기하급수적으로 분산이 줄어드는 것을 확인할 수 있다. 따라서 큐빗 수가 커질수록 BP는 더 심화되고, 어느 순간은 양자컴퓨터에서 발생하는 오차보다 gradient가 작아져서 학습조차 불가능해질 수 있다.

실습

간단한 파이썬 코드를 통해 Barren Plateau가 실재함을 확인해 보자. 우선 아주아주 간단한 회로를 제작해 보자. 각 레이어는 Rx게이트로만 이루어져 있고, 작용이 끝난 뒤엔 CNOT게이트를 인접한 큐빗 사이에 작용한다. 또한 문제상황을 최대로 단순화하기 위해 관측값은 0번째 큐빗의 PauliZ로 사용하였다. 위 내용을 pennylane코드로 구현하면 아래와 같다.

# 페니레인을 사용하여 양자 회로 정의
n_qubits = 8
dev = qml.device("lightning.qubit", wires=n_qubits)

@qml.qnode(dev)
def quantum_circuit(params):
    # params: (n_layers, n_qubits) shape
    for layer in params:
        for i in range(len(layer)):
            qml.RX(layer[i], wires=i)
        for i in range(len(layer)):
            qml.CNOT(wires=[i, (i+1)%n_qubits])
    return qml.expval(qml.PauliZ(0))

큐빗 수를 다르게 하기 위하여 dev는 넉넉하게 8큐빗으로 만들었다. 큐빗 개수가 작다면, 일부만 사용하면 되므로 문제 없다.

이제 큐빗 수, 레이어 수를 다르게 하면서 gradient를 계산하고, 기록하는 코드만 추가하면 된다. 이는 아래와 같다.

# 아래 코드는 20초 이내로 실행됩니다
mean_recorder = []
std_recorder = []
xs = range(3, 9)
layers = range(2, 5)
for n_layers in tqdm(layers):
    means = []
    stds = []
    print(f"processing {n_layers} layers")
    for n_qubits in xs:
        print(f"processing {n_qubits} qubits")
        gradients = []
        for rep in range(100//n_qubits):
            params = np.random.normal(-np.pi, np.pi, (n_layers, n_qubits), requires_grad=True)
            # 양자 회로를 실행하고 그라디언트 계산
            circuit_value = quantum_circuit(params)
            gradient = qml.grad(quantum_circuit)(params)
            for grad in gradient:
                gradients.append(grad)
        means.append(np.mean(gradients))
        stds.append(np.std(gradients))
    mean_recorder.append(means)
    std_recorder.append(stds)

위 코드를 실행하면 recorder변수에 큐빗 수와 레이어 수에 따른 gradient의 평균, 표준편차를 기록한다. 이제 그래프를 통해 결과를 확인해 보자.

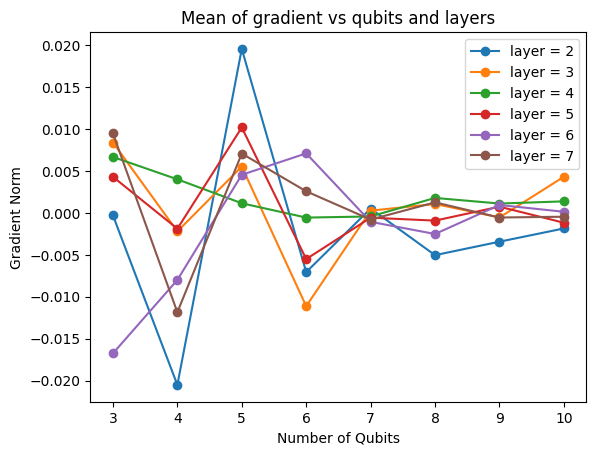
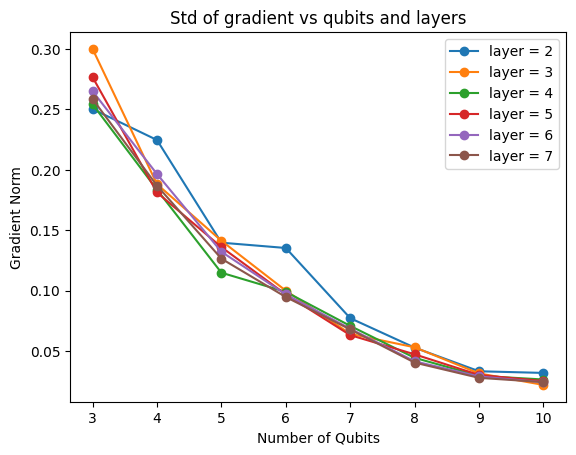
문제상황을 너무 간략하게 만들어서 scale은 맞지 않을 수 있지만, 큐빗 수가 늘어날수록 gradient의 평균이 0으로 수렴하는 것을 확인할 수 있다. 또한 큐빗 수가 늘어날수록 griadnet의 분산은 빠르게 감소하였다. 흥미로운 점은, 이 현상은 레이어 수와는 상관 없이 큐빗의 수에만 연관된 현상이라는 점이다. 이것은 논문 [1] 의 결과와 일치한다.

결론

이 글에서는 양자 인공신경망에서 발생하는 Barren Plateaus에 대해 다루었다. 이 현상은 큐빗 수가 늘어날수록 gradient의 평균이 0으로 수렴하고, 분산이 빠르게 감소하는 현상이다. 이 현상은 양자컴퓨터에서 사용되는 측도 집약화 현상 때문에 발생한다. 이 현상은 큐빗 수가 늘어날수록 더욱 심화되므로, 이 문제를 해결하지 않고서는 일반적인 양자 인공신경망의 학습이 어려워질 것으로 예상된다.

하지만 BP를 피해가기 위해 다양한 접근법이 시도되고 있다. BP를 피해갈 가능성이 있는 이유는 다음과 같다.

• 사용한 Unitary가 완전히 랜덤한 분포에서 추출되었음을 가정하였다. 만약 특수한 group의 게이트들만 사용하여 회로를 구성한다면 BP를 피해갈 수 있다. 대표적으로 qcnn에서는 BP가 발생하지 않음이 알려져 있다.
• Observable H를 global한 것으로 간주하였음. 만약 local하다면 측도 집약화 현상이 덜 일어나므로 BP가 완화된다.
• 회로의 초기화를 잘 한다면 측도 집약화 현상에서 적도를 피해갈 수 있다.

따라서 BP는 충분히 해결 (또는 우회)할 가능성이 있는 문제라고 생각하며, 언젠가는 일반적인 방법론이 등장하여 양자 인공신경망의 한계를 극복할 것이라 생각한다.

참고문헌

[1] McClean, Jarrod R., et al. “Barren plateaus in quantum neural network training landscapes.” Nature communications 9.1 (2018): 4812. [2] https://www.tensorflow.org/quantum/tutorials/barren_plateaus?hl=ko [3] Puchałla, Z. & Miszczak, J. A. Symbolic integration with respect to the haar measure on the unitary groups. Bull. Pol. Acad. Sci. Tech. Sci. 65, 21 (2017).