양자컴퓨팅으로 PS하는법

quantum , quantum-computing , ps , problem-ssolving

제목을 조금 자극적이게 “양자컴퓨팅으로 PS하는 법”이라고 설명했지만, 아직 일반적인 PS를 하는 데 양자컴퓨터를 사용하는것은 어렵다. 그래도 그나마 PS스러운 max cut 문제를 양자컴퓨터로 해결하는 방법을 최대한 쉽게 소개하고자 한다. 나중에도 양자컴퓨터를 사용한 소개할만한 알고리즘이 있다면 소개해볼 계획이다.

Max cut 문제란?

Max cut 문제는 주어진 그래프를 두 집합으로 잘 분리하여 두 집합 사이를 연결하는 간선의 수를 최대화하는 문제이다.

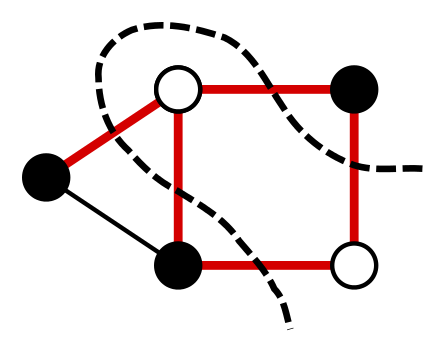
그림 1. Maxcut 예시.흰색과 검은색 정점 집합으로 위와 같이 분리하면 둘 사이를 연결하는 간선(빨간색)이 5개로 최대가 된다. 따라서 이 그래프에서 maxcut 은 5이다.

이 문제를 다항 시간에 해결할 수 있을 지 없을 지 잠시 고민해 보자. 아마 방법이 떠오르지 않을 것이다.

그리고 만약 누군가가 주어진 복잡한 그래프의 max cut이 10204531이라고 주장했다고 해 보자. 그래도 친절하게 어떻게 정점 집합을 분리해야 저 답이 나오는지는 제공했다고 치자. 그럼 저 그래프의 max cut이 실제로 10204531인지를 다항 시간에 검증할 수 있을까? 정점 집합을 제공받았으니 직접 카운팅 해서 해당 경우에 cut이 10204531이라는 건 확인할 수 있을 것이다. 그러나 저거보다 더 큰 값이 불가능하다는 것을 검증하기는 굉장히 힘들 것만 같다…

위 두 가지 문제를 통해 직감적으로 느꼈듯, 일반적인 그래프에 대해 max cut을 다항 시간에 구할 수도 없고, 다항 시간에 답을 검증할 수도 없다. 따라서 이 문제는 NP-hard 문제이다. 증명은 이 글의 목적에는 맞지 않으므로 넘어가자.

Max cut의 근사 알고리즘

정확한 답은 절대로 다항 시간에 구할 수가 없기 때문에, 주된 연구 방향은 근사 알고리즘이다. 예를 들어, 주어진 그래프의 max cut이 M이고 어떤 알고리즘으로 구한 답이 A일 때, $A/M > 0.7$ 을 보장할 수 있다면 이 알고리즘은 0.7-approximation algorithm이라고 한다. 0.879-approximation 알고리즘은 다항 시간에 구할 수 있다는 것이 알려져 있다[1]. 하지만 이번 글의 목적은 양자 알고리즘을 소개하는 것이다. 하지만 양자 알고리즘으로도 max cut문제를 다항 시간에 해결할 수 없다. 양자 알고리즘으로도 아직까지는 approximation 알고리즘이 한계이며, 이 알고리즘을 소개해보고자 한다.

Max cut을 양자 알고리즘으로 해결하기

아래는 이제부터 설명할 hamiltonian, QAOA의 아주 간략한 개론이다.

각 정점을 어느 집합에 넣을지는 둘 중 하나이다. 두 집합으로밖에 분할하지 못하기 때문이다. 따라서 양자 상태로 쉽게 대응시킬 수 있다. 그 다음엔 양자 상태에서 cut의 개수를 구하는 방법이 필요하다. 이것은 hamiltonian이란 것을 정의함으로써 해결된다. 그 다음으론 hamiltonian을 최대화 시키는 양자 상태를 찾으면 된다. 이는 QAOA를 사용한다.

1. 양자 상태로 표현하기

Max cut 문제의 본질은 그래프의 정점을 두 부분집합으로 분할하는 것이다.

그림 2. 앞으로 예시로 들 그래프.

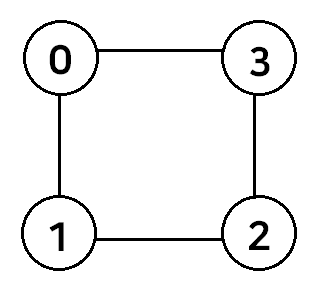
위 그래프는 정점을 4개 가지고 있다. 그리고 누가 보아도 maxcut은 4이다. 0, 2번 정점과 1, 3번 정점을 서로 다른 집합으로 나누면 된다.

이제 문제를 해결하기 위해 큐비트 4개를 준비할 것이다. 그래프의 정점이 n개라면 n개의 큐비트를 준비하면 된다.

그리고 $0 \leq i \lt n$인 정수 i에 대해 i번째 큐비트는 i번째 정점이 어느 집합에 속하는지에 대한 정보를 저장할 것이다. 집합은 두 개 뿐이므로 $\vert0\rangle$, $\vert1\rangle$로 나누자. 같은 값을 가진다면 같은 집합에 속하는 것이다.

그렇다면, 이 문제의 답이 되는 양자 상태는 $\vert0101\rangle, \vert1010\rangle$일 것이다. 이제 우리는 저 양자 상태만 확률을 최대화하여 남겨 놓고, 나머지 상태들은 확률을 없애버리는 것이 목표이다. 이후엔 관측을 통해 양자 정답 상태를 구할 수 있고, 이로부터 max cut을 구할 수 있다. 그렇다면 어떻게 저 상태들만 남기고 나머지 상태들을 지울 수 있을까? Hamiltonian을 사용하면 된다.

2. 헤밀토니안 정의하기

양자 컴퓨팅에서 Hamiltonian이란 양자 상태를 넣으면 그 상태의 에너지가 나오는 Observable이다. 물론 관측값일 뿐이므로, 명칭이 ‘에너지’라고 해서 실제로 양자 상태의 에너지를 의미하지는 않는다. 우리가 정의하기 나름이다.

이런 류의 문제 상황에서 전형적인 문제해결의 방법은 다음과 같다.

문제 상황에 대응되는 Hamiltonian을 만드는데, 바닥상태가 문제의 정답이어야 한다.
여러 가지 방법을 써서 바닥상태(정답)를 찾는다.

위 기준에 따르면 우리의 목표는 $\vert0101\rangle, \vert1010\rangle$가 바닥상태가 되는 Hamiltonian을 설계하는 것이다. 일반화한다면, cut의 개수가 많아질수록 에너지가 낮아지는 Hamiltonian을 설계 하면 바닥 상태가 항상 문제의 정답이 될 것이다.

2.1 Motivation

정점 i가 속한 집합을 $c_i$ 라고 표기하자. 그리고 어느 집합에 속하는지에 따라서 $c_i = $ 1 또는 -1 값을 배정하자. maxcut에 해당하는 경우는 $c_0, c_1, c_2, c_3 = -1, 1, -1, 1$ 또는 $c_0, c_1, c_2, c_3 = 1, -1, 1, -1$ 이다.

그리고 그래프의 연결 상태를 표현한 인접행렬 $a_{ij}$는 정점 i와 정점 j가 간선으로 바로 연결되어 있으면 1, 아니면 0이라고 하자. 그렇다면 주어진 집합 배정 ${c_i}$에 의해 결정되는 cut의 개수는 다음과 같은 식으로 계산할 수 있다.

\[C = \frac{1}{2}\sum_{i \leq j}{a_{ij}(1-c_ic_j)}\]

쉬운 식이지만 조금만 첨언하자면, 정점 i, j가 같은 집합이라면 $c_i c_j=1$이므로 더해지는 값이 0이고, 둘 사이의 간선도 존재하면서 $c_i c_j = -1$일 때 2가 더해진다. 그래서 $\frac{1}{2}$ 을 곱해서 맞춰주는 것이다.

2.2 Hamiltonian설계

위 식을 그대로 적용한 Hamiltonian을 만들어 보자. 양자 상태가 $\vert0\rangle$ 일때는 1, $\vert1\rangle$일때는 -1이 되는 걸 떠올려 보면 Z operator가 떠오른다. $Z\vert0\rangle = 1, Z\vert1\rangle = -1$ 이기 때문이다. (또는 $Z = \sigma_z = \begin{pmatrix}1&0\0&-1\end{pmatrix} $ 로 표기하기도 함)

이제 Hamiltonian을 설계해 보자

\[H = \frac{1}{2}\sum_{i \leq j}{a_{ij}(1-Z_i Z_j)}\]

이면 된다. 이 Hamiltonian이 바로 양자 상태를 cut의 개수로 매핑시켜 주는 Observable이다. 그런데 우리는 이를 에너지로 해석하고, 바닥 상태를 구하고 싶다. 따라서 부호를 음수로 만들어주면 된다.

\[H = -\frac{1}{2}\sum_{i \leq j}{a_{ij}(1-Z_i Z_j)}\]

또는 아래와 같은 식으로도 적을 수 있다. ($E$는 $(i, j)$형태의 무방향 간선들을 포함하는 간선들의 집합)

\[H = -\frac{1}{2}\sum_{i, j \in E}{(1-Z_i Z_j)}\]

이제 이 Hamiltonian의 바닥 상태를 구하면 문제의 답을 구하는 것이다.

2. 바닥 상태를 구하기

Hamiltonian을 구했으니 바닥 상태를 구할 때이다. 보통 이럴 때에는 Variational Quantum Circuit을 사용한다. VQC에 대한 설명은 https://infossm.github.io/blog/2023/06/25/variational-algorithm/ 이 글에 설명이 되어 있다.

간단하게 설명하자면 파라미터화된 양자 회로를 만들고, 파라미터들의 gradient를 구해서 값을 줄이는 방향으로 파라미터를 업데이트 해 나가는 알고리즘이다. 머신 러닝과 동일한 접근방식이다.

다만 여기서는 VQC의 종류 중 하나인 QAOA를 사용한다. Quantum approximate optimization algorithm(QAOA)는 우리가 바닥 상태를 잘 알고있는 hamiltonian을 준비하는 과정으로부터 시작한다. 그리고 초기 양자 상태는 그 hamiltonian의 바닥 상태로 설정한다. 그리고 점진적으로 답을 구하고 싶은 hamiltonian으로 변화시켜 나가고 바닥상태도 점진적으로 변화시켜 나가는 방식이다. 최종적으론 우리가 원하던 바닥상태를 구할 수 있게 된다.

하지만 이 방식은 결정론적 방식이 아니다. 사실 대부분의 양자 알고리즘이 그렇다. 그렇기에 이름에 approximate라는 단어가 그렇다는 것이고, 구체적으로는 hamiltonian을 이동시켜 감에 따라 바닥상태가 제대로 이동하지 않고 local minimum에 빠질 수도 있다. 이 확률적인 바닥 상태의 전이로 인해 여러 번 실행하여 답을 찾아야 한다.

이제 구체적인 코드와 함께 max cut의 바닥 상태를 계산하는 여정을 따라가 보자.

QAOA란?

풀고자 하는 문제를 hamiltonian으로 정의하고 바닥 상태를 찾는 과정을 통해 문제의 해답을 찾는 것은 일반적인 접근방식이다. 하지만 게이트 기반 양자컴의 모든 연산은 우리들이 “임의적”으로 가해 주어야 하는 것들이다. “hamiltonian을 구성했으니, 가만히 놔두어도 바닥 상태를 찾아 가게 할 것이다” 이런 생각은 잘못된 생각이다. 적어도 gate 기반 양자 컴퓨터에서는 그렇다. 우리는 직접 양자 상태가 바닥 상태가 되도록 입력 상태에 연산을 가해서 바닥 상태로 만들어 주어야 한다.

그러나 현재의 양자 컴퓨터는 에러가 너무 크고, 큐빗도 작다. 이를 NISQ(Noisy Intermediate-Scale Quantum) 시대의 양자 컴퓨터라고 부른다. 따라서 에러에 강건한 양자 알고리즘을 사용하는게 유리하다. 사실 필수인 수준이다. 에러가 무시 가능한 시대가 온다면 사용하는 리소스가 중요하겠지만, 지금은 에러의 규모는 그 알고리즘의 가능/불가능을 나누는 중요한 척도이다. 이러한 상황에서 나온 알고리즘이 QAOA이다.

QAOA는 위에서 잠깐 언급했듯이, 우리가 바닥상태를 잘 알고 있는 hamiltonian에서부터 시작한다. 주로 바닥 상태는 maximally mixed state ($\frac{1}{2^n}\sum_{i=0}^{2^n-1}\vert i\rangle$)에서 시작하고, 대응되는 hamiltonian은 $\sigma_x^{\otimes n} = \begin{pmatrix}0&1\1&0\end{pmatrix}^{\otimes n}$)

그리고 hamiltonian을 우리가 바꾸고 싶은 $H$로 바꿔야 하는 데, 이를 점진적으로 바꾸어 나가 안정적으로 바닥 상태를 찾는 것이 목표이다.

이 과정은 의외로 간단한데, 작은 수 $\beta, \gamma$에 대해서 초기 hamiltonian이 $X$, 목표 hamiltonian이 $Y$라면

\[e^{-i\beta X}e^{-i\gamma Y}\]

를 연속적으로 가해 주면 된다. 만약 l개의 레이어를 사용한다면 $\beta, \gamma$는 각각 p개의 원소를 가진 파라미터일 것이다. 큐빗 수는 4개인데, 이번 예시에서 든 그래프의 정점 수가 4개이기 때문이다. 이제 구현을 살펴보자.

QAOA for maxcut의 구현

먼저 기본적인 세팅부터 하자.

import pennylane as qml
from pennylane import numpy as np

np.random.seed(1108)

edges = [(0, 1), (0, 3), (1, 2), (2, 3)]
n_qubits = 4 # 정점 수 = 큐빗 수

이제 $\sigma_x$와 $H$ 연산을 가해주는 레이어를 정의하자.

# 초기 hamiltonian 적용 레이어
def U_B(beta):
    for wire in range(n_qubits):
        qml.RX(2 * beta, wires=wire)


# 목표 hamiltonian 적용 레이어
def U_C(gamma):
    for edge in edges:
        qml.CNOT(wires=[edge[0], edge[1]])
        qml.RZ(gamma, wires=edge[1])
        qml.CNOT(wires=[edge[0], edge[1]])

사용할 backend는 pennylane에서 제공하는 lightning.qubit이다. 빠른 연산을 지원한다. 나중에 샘플링을 직관적으로 하기 위해서 shots=1로 하였다. 만약에 여러 번의 샘플링을 한 번에 하고 싶다면 shots를 늘리고 추가적인 후처리를 하면 된다.

dev = qml.device("lightning.qubit", wires=n_qubits, shots=1)

이제 본격적으로 모든 일이 일어나는 회로를 정의할 것이다. 처음에는 모든 큐빗에 Hadamard gate를 적용하여 maximally mixed state를 만드는 것으로 시작한다. 그 다음엔 현재 edge가 만드는 cost를 계산하기 위한 evaluation term이 있다. 만약 edge가 없다면 상태 하나를 샘플링하는 동작을 수행한다.

@qml.qnode(dev)
def circuit(gammas, betas, edge=None, n_layers=1):
    # Hadamard게이트를 가해서 초기 |+> 상태 준비
    for wire in range(n_qubits):
        qml.Hadamard(wires=wire)
    # 레이어 적용 
    for i in range(n_layers):
        U_C(gammas[i])
        U_B(betas[i])

    if edge is None:
        return qml.sample() # 샘플링 모드

    # edge 하나에 대한 evaluation term
    H = qml.PauliZ(edge[0]) @ qml.PauliZ(edge[1])
    return qml.expval(H)

마지막으로, 파라미터들을 최적화 하야 답을 찾아내는 과정이 필요하다. (2, n_layers)차원의 벡터가 파라미터이다. 절반은 $beta$, 나머지 절반은 $gamma$이다. 보면 objective 함수 내에서 edge들을 순회하면서 가중치를 더하는 것을 볼 수 있다. Hamiltonian의 기댓값을 한 번에 계산하는 것은 힘들기 때문에, 여러 개로 쪼개서 구한 뒤 더하는 것이다. 어차피 gradient를 구할 때에는 영향을 주지 않는다.

최적화는 30번 진행하고, 이 단계가 끝난 뒤에는 샘플링을 100번 진행하여 가장 많이 등장하는 상태를 출력한다. 이 상태가 답이 된다.

def qaoa_maxcut(n_layers=1):
    print("\nnumber of layers={:d}".format(n_layers))

    # QAOA 파라미터는 작은 값으로 초기화됨.
    params = 0.01 * np.random.rand(2, n_layers, requires_grad=True)

    # 목적함수 정의
    def objective(params):
        gammas, betas = params[0], params[1]
        obj = 0 # 목적함수 (-씌워진 상태)
        for edge in edges: # 각각 edge별로 따로 목적함수 계산.
            obj -= 0.5 * (1 - circuit(gammas, betas, edge=edge, n_layers=n_layers))
        return obj

    opt = qml.AdagradOptimizer(stepsize=0.5) # optimizer

    # 파라미터 최적화 코드
    steps = 30
    for i in range(steps):
        params = opt.step(objective, params)
        if (i + 1) % 5 == 0:
            print("{:5d}이후 목적합수: {: .7f}".format(i + 1, -objective(params)))

    # 가장 많이 등장하는 상태가 바닥 상태 --> 100개 샘플링 해보자.
    bit_strings = []
    for i in range(0, 100):
        bits = circuit(params[0], params[1], edge=None, n_layers=n_layers).numpy()
        bit_strings.append(''.join([str(int(b)) for b in bits]))
    
    print("가장 많이 등장하는 상태: ", most_common(bit_strings))

이제 아래 코드처럼 레이어 개수를 다르게 해보면서 실행해 볼 수 있다. 위 그래프는 단순해서 레이어가 하나여도 답을 잘 찾는다.

qaoa_maxcut(n_layers=1)
qaoa_maxcut(n_layers=2)
qaoa_maxcut(n_layers=3)

레이어가 하나일 때, 아래와 같은 출력이 나온다. 목적함수가 4일 때가 최대인데, 중간중간에 항상 4이지는 않는 것도 확인할 수 있다. 최빈값이 4일 뿐이다. QAOA가 확률적인 최적화 과정이란 것을 여기서도 확인할 수 있는 것이다.

number of layers=1
    5이후 목적합수:  1.0000000
   10이후 목적합수:  4.0000000
   15이후 목적합수:  2.0000000
   20이후 목적합수:  2.0000000
   25이후 목적합수:  3.0000000
   30이후 목적합수:  2.0000000
가장 많이 등장하는 상태:  1010

이제 좀 더 복잡한 그래프를 만들어서 테스트 해 보자.

그림 3. 좀 더 복잡한 그래프.

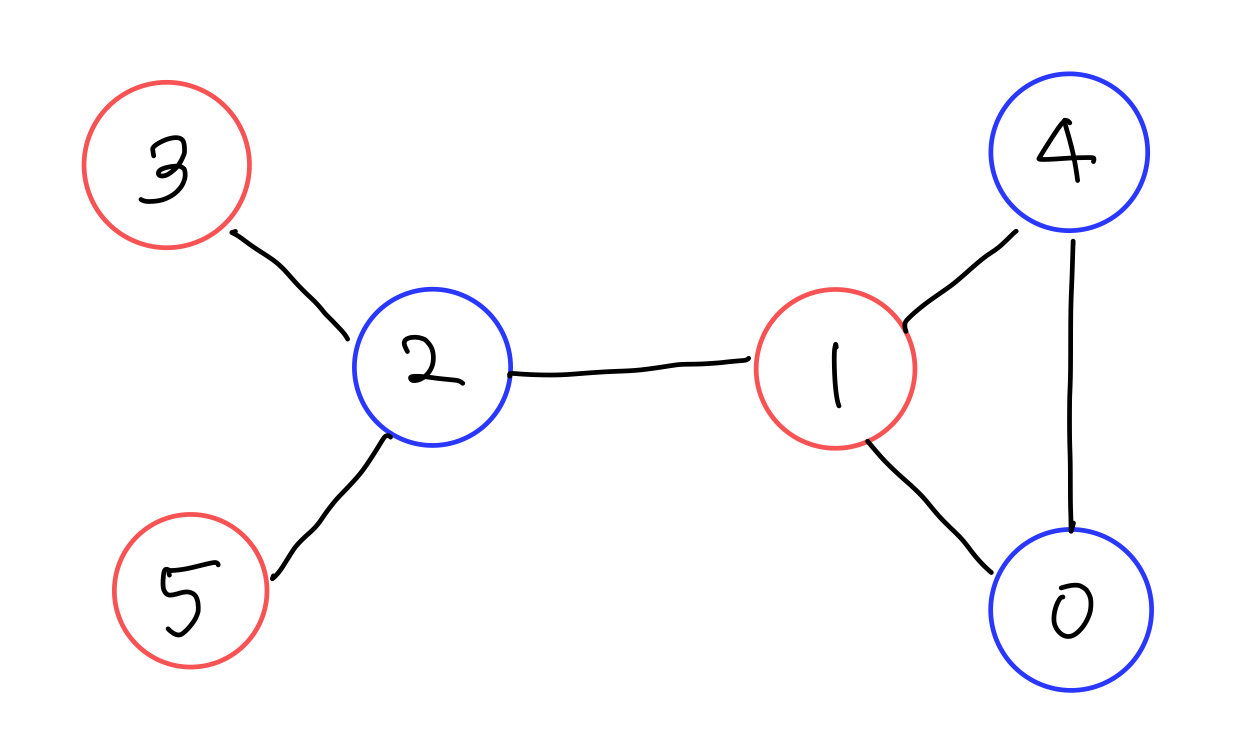
정점의 개수는 6개 이므로 사용할 큐비트는 6개 이다. maxcut은 5인데, 사진에서 정점을 색칠해놓은게 최대 maxcut을 만드는 예시이다. bitstring으로 나타내면 101010, 010101 둘 중 하나이다.

이번에는 레이어를 3개는 써야지 답이 나온다.

number of layers=3
    5이후 목적합수:  3.0000000
   10이후 목적합수:  4.0000000
   15이후 목적합수:  6.0000000
   20이후 목적합수:  3.0000000
   25이후 목적합수:  5.0000000
   30이후 목적합수:  4.0000000
가장 많이 등장하는 상태:  101010

만약에 레이어를 2개만 사용한다면 답을 찾지 못하였다.

number of layers=2
    5이후 목적합수:  3.0000000
   10이후 목적합수:  4.0000000
   15이후 목적합수:  3.0000000
   20이후 목적합수:  4.0000000
   25이후 목적합수:  3.0000000
   30이후 목적합수:  3.0000000
가장 많이 등장하는 상태:  011000

흥미로운 관찰거리가 있다. 레이어 3개인 경우를 살펴보자. 분명히 max cut은 5인데, 중간에 목적함수가 6까지 올라가는 경우가 있다. 어떻게 이럴 수 있을까? 이건 hamiltonian은 양자 상태 기반이기 때문이다. 다양한 양자상태의 중첩을 시키게 되면 두 집합을 모두 점유하는 상태도 가능하기 때문에 목적함수의 이론적 최댓값을 달성할 수도 있다. 하지만 우리가 실제로 관측하는 상태는 중첩이 붕괴된 상태이기 모순되는 것은 아니다.

결론

간단하게 결론을 요약해 보자.

Max cut문제는 양자상태의 에너지에 대응되는 hamiltonian으로 쉽게 변환된다.
바닥상태를 찾는 것이 문제의 해답을 찾는 것이다.
바닥상태를 찾을 때 QAOA를 사용하면 적은 파라미터로 안정적으로 찾을 수 있다.

참고문헌

[1] Goemans, Michel X., and David P. Williamson. “. 879-approximation algorithms for max cut and max 2sat.” Proceedings of the twenty-sixth annual ACM symposium on Theory of computing. 1994. [2] https://pennylane.ai/qml/demos/tutorial_qaoa_intro/ [3] https://pennylane.ai/qml/demos/tutorial_qaoa_maxcut/ [4] https://qml.baidu.com/tutorials/combinatorial-optimization/solving-max-cut-problem-with-qaoa.html