January 26, 2024 00:00

올해 1월 18일, Learning shallow quantum circuits라는 제목의 연구가 arxiv에 올라왔고, 가장 큰 양자정보 학회인 QIP에서 해당 논문을 가지고 발표까지 진행되었다. 이 연구는 양자 회로를 학습하던 방식을 바꿔놓을 가능성이 있는 연구이고, 어쩌면 Quantum Machine Learning(QML)의 미래 자체에 영향을 줄 수도 있을것 같아 보인다. 굉장히 좋은 아이디어도 얻어갈 것이 많은 연구라고 생각하여서 공유해보고자 한다.

요약

이 논문에서 해결하고자 하는 문제는 두 가지이다.

1. Unknown unitary $U$에 여러 입력으로 여러 번 접근할 수 있을 때, 최대한 가까운 unitary $\hat{U}$를 찾는 것. (diamond distance 기준)
2. Unknown unitary $U$에 넣을 수 있는 입력은 $\vert 0\rangle$ 뿐이고, 그 결과 $\vert \psi \rangle = U\vert0\rangle$을 여러번 관측할 수 있을때, $\vert \psi \rangle$를 최대한 잘 근사하는 unitary $\hat{U}$를 찾는 것. (trace distance 기준)

사실 quantum process tomography와도 동일한 목표를 공유하고 있다. 이 연구 결과를 다르게 생각해 본다면 우리가 알아내고자 하는 unknown process가 얕은 깊이의 양자 회로라면 효율적으로 알아낼 수 있다는 의미이다.

이 논문에서 사용한 핵심적인 아이디어는 local inversion과 circuit sewing을 사용해서 global inversion을 구현하는 것이다. 다음과 같이 풀어서 설명할 수 있다.

각 큐빗에 대해서 $U$의 영향을 제거하는 것을 부분적 역함수라는 의미에서 local inversion이라고 한다. 모든 큐빗 각각에 대해 local inversion을 구해 놓는다면 이를 잘 사용해서 전체 큐빗들에 대해 $U$의 영향을 되돌리는 global inversion을 구할 수 있다! 여기에 쓰는 테크닉을 circuit sewing이라고 한다.

이제 자세하게 알아보자.

배경

임의의 unitary $U$에 대해 $UV=1$ 인 unitary $V$를 구하면 $U$의 global inversion을 구한 것이다. 사실 그냥 $U$의 역행렬을 구한 것이다. 그런데 우리는 $U$를 어떻게 구성해야 하는지 모른다. 물론 기본적인 게이트들 Rx, Ry, Rz, CNOT 을 써서 모든 unitary를 구현 가능하단 건 증명되어 있지만, 어떻게 구성해야 할지를 모르는 것이다.

그렇다면 U의 반대 프로세스인 $U^\dagger = V$를 우리가 편하게 다룰 수 있는 Rx, Ry, Rz, CNOT들을 사용해서 알아낸다면 어떨까? $V^\dagger = U$이므로 $V$를 구성한 게이트 순서들을 뒤집고, 파라미터들도 뒤집으면 $U$를 알아낼 수 있다. 일단 양자 회로로 표현하기만 하면 inverse process를 구하는 건 너무 쉬운 일이다.

그런데 $U$를 모르는데 $V$를 구하는 게 쉬울 리가 없다. 그런데 이 논문에서는 다항 시간에 $V$를 찾을 수 있는 방법을 제공한다. 그 방식은 다음과 같다.

local inversion & circuit sewing

전체 Unitary의 inverse를 구하는 건 어렵다. 그런데 각 큐빗에 대해서 Unitary의 효과를 되돌려놓는 local inversion을 구하는건 쉽다. 그렇다면 각 큐빗별로 구해놓은 local inversion을 활용해서 전체 Unitary의 inverse를 구하는 방법은 없을까?

위 질문에 대한 답은 가능하다이다. 아주 멋진 아이디어를 사용한다. 먼저 local inversion에 대해 정확하게 정의하자.

$U$가 0번째 큐빗부터 n-1번째 큐빗까지 작용할 때, i-th local inversion of $U$ 는

를 만족하는 unitary $V_i$이다. 여기서 $\text{tr}_{\neq i}$는 $i$번째 큐빗을 제외한 나머지 큐빗들에 대한 partial trace를 의미한다. 즉, $V_i$는 $U$의 효과를 $i$번째 큐빗에 대해서만 되돌려놓는 unitary이다.

이제부터 local inversion을 사용한 circuit sewing 프로세스를 설명하겠다. 기억해두어야 할 점은, 이 과정에서는 $\vert 0\rangle$ 로 초기화되어 있는 추가적인 큐빗 n개가 필요하다는 점이다. 0번째 ~ n-1번째 큐빗이 우리가 집중해야 할 큐빗들이고, n번째 ~ 2n-1 번째 큐빗이 추가 큐빗이다.

이제 시작 상태 $\vert 0\rangle^{\otimes n}$에서 $U$를 가한 상태 $U\vert 0\rangle^{\otimes n}$에서 시작하자. 여기에 $V_0$을 가한다면, 0 번째 큐빗은 $\vert 0 \rangle$이 되고, 나머지 큐빗들은 $\text{tr}_{0}\left [ V_0 U(\vert 0\rangle \langle 0\vert)^{\otimes n}U^\dagger V_0^\dagger \right ]$ 의 상태가 된다. 이제 0번째 큐빗을 n번째 큐빗(추가 큐빗) 과 swap한다. 그 다음 $V_0^\dagger$를 가한다.

이제 상태는 결과적으로 다시 $U\vert 0\rangle^{\otimes n}$로 돌아온다. 그런데, 0번째 큐빗을 $\vert 0 \rangle$로 되돌린 효과를 얻은 것이다. 이제 1번째 큐빗에 대해서도 같은 과정을 반복한다. $V_1$을 가하고, 1번째 큐빗과 n+1 번째 큐빗을 swap하고, 다시 $V_1^\dagger$ 을 가해서 상태를 복구하는 것이다. 이걸 n-1번째 큐빗까지 가한다면 $\vert 0 \rangle ^ {\otimes n}$ 상태를 n~2n-1번째 큐빗에 저장하게 된다.

이 과정이 어떤 과정일까?

이 전체 과정을 $V^{sew}$라고 한다면 $V^{sew}$는 2n개의 큐빗에 가한 유니터리 프로세스이다. 그 결과는

이다. 여기서 U는 0~n-1번째에 가해진 U이고, $U^\dagger$는 n~2n-1번째에 가해진 U의 inversed이다.

왜 이렇게 되는 것일까? 아주 기초적인 조작들만 사용해서 만들어낸 과정이기 때문에 조금 곱씹어 보면 이해하기 어렵지 않을 것이다. 각각의 큐빗별로 작용을 되돌린 다음, 되돌아간 큐빗들을 미리 저장해두었을 뿐이다. 그 과정에서 하나하나 차근차근 큐빗들을 모아가기 위해 swap게이트를 사용하였다.

전체 과정을 수식으로 다시 표현하자면 $V_i$ 는 $UV_i = U’^{(i)}\otimes I_i$ 를 만족하는 i번째 큐빗의 local inversion일 때,

이 식이라고 할 수 있다 (논문에서는 1-based라서 $i=1$ 부터라고 적혀 있다).

간단한 의사 코드로도 살펴 보자. 훨씬 직관적으로 이해할 수 있을 것이다.

U() # 처음 게이트를 가함
for i in range(n):
    V_i() # i번째 큐빗을 분리해냄
    SWAP(i, n+i) # 바꿔치기
    V_i_dagger() # 다시 V_i를 복구함

local inversion 구하기

그럼 local inversion은 어떻게 구할까? Parameterized Quantum Circuit을 사용하면 된다. QML에서 흔히 사용하듯이 적당히 Rx, Ry, Rz, CNOT 사용해서 회로를 구성하고 gradient구해서 최적화하면 된다. 학습 목표는 i번째 큐빗을 $\vert 0\rangle$으로 만드는 것이다.

이렇게 학습한 회로 자체가 $V_i$가 되는 것이다. 이 방식으로도 $V_i$를 다항 시간, 다항 개수의 게이트로 찾을 수 있다는 것에 대해서 논문에서 증명되어 있다.

Learning shallow quantum circuits

사실, 위 과정에서 해결한 것은 $V^{sew}$ = $U \otimes U^\dagger$인 $V^{sew}$를 찾은 게 아니라,

를 만족하는 $V^{sew}$를 찾은 것이다. 하지만 이것만으로는 $U$를 찾았다고 할 수 없다. $\vert 0\rangle$에 대한 동작이 동일한 다른 프로세스 하나를 찾았을 뿐이다. 물론 이것만으로도 의미 있는 연구지만, 논문의 자극적인 제목에는 맞지 않는다. 더 나아가야 한다.

논문에서 복잡한 증명과정을 통해 저자는 위 과정을 잘 수행하기만 해도 $U$를 문제 없이 다항 시간에 찾을 수 있음을 보이고 있다. 그 ‘잘’을 위해서 Heisenberg-evolved Pauli operators를 소개한다.

Sewing Heisenberg-evolved Pauli operators

엄밀한 증명이 너무 복잡한 관계로 이 부분 또한 간략하게 아이디어만 소게하도록 하겠다.

이번 섹션의 목표는 $U^\dagger P_i U$를 구하는 것이다. 여기서 $P_i$는 i-th 큐빗에만 가해지는 Pauli operator이다. 이를 구하는 건 간단하다.

stabilizer product state $\vert \psi \rangle$를 준비한다. 그 상태에 U를 가하고, 동일한 확률의 pauli basis $X, Y, Z$로 관측한다. 이 과정을 통해 $\langle \psi \vert U^\dagger P_i U \vert \psi \rangle$를 구할 수 있다. 서로 다른 stabilizer state를 입력으로 넣어서 기댓값을 관측하는 과정을 반복하면 $U^\dagger P_i U$를 구할 수 있다.

그 다음 중요한 관찰은 SWAP게이트에 대한 웰노운 관계식을 떠올리는 것이다.

위 식은 연습지를 펴고 조금만 써보면 아주 쉽게 보일 수 있다. 이제 $S_i$를 i-th 큐빗과 i-th ancilla qubit간의 SWAP 게이트라고 정의하자. (i번째 큐빗과 n+i번째 큐빗의 SWAP 게이트이다). 그리고 $W_i \coloneqq U^\dagger S_i U = \frac{1}{2} \sum_{P \in I,X,Y,Z} U^\dagger P_i U \otimes P$ 로 정의하자. 바로 위에서 stabilizer product state를 통한 관측을 통해 $U^\dagger P_i U$를 구할 수 있었으므로 $W_i$도 쉽게 구할 수 있다.

앞에서 다루었던 sewing을 통해 최종적으로 만들고자 했던 프로세스는 $U \otimes U^\dagger$였다. 이제 $W_i$를 사용해서 이 프로세스를 표현해볼 것이다.

임을 리마인드 하자. 이제 다음 식이 성립한다.

따라서

가 성립한다. 사실 이 관계는 자명한데, 마지막 식을 관찰해 보면 $U^\dagger U$가 계속 상쇄되기 때문에 $SU^\dagger SU$만 남게 되는데, 사실 $U \otimes U^\dagger = SU^\dagger SU$ 임은 자명하다. 아래 그림으로도 이 자명함을 확인해 볼 수 있다.

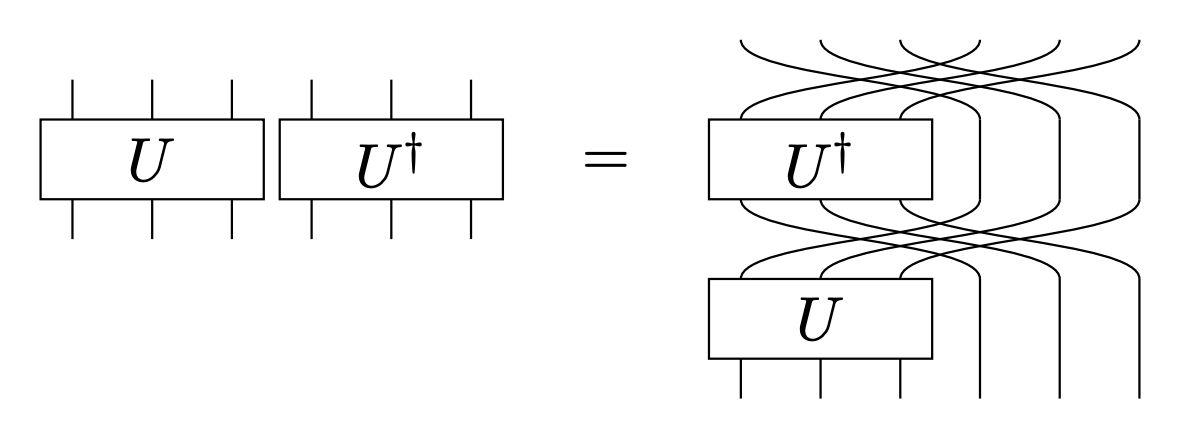
결론적으로, outline을 설명하자면 다음과 같다.

1. 관측을 통해 $U^\dagger P_i U$를 구한다.
2. 위에서 구한 값을 사용하여 $W_i$들을 계산한다
3. $U \otimes U^\dagger = S \prod_{i=0}^{n-1} W_i$ 관계식으로부터 $U \otimes U^\dagger$를 구한다.

이렇게 unknown unitary를 알아낼 수 있다.

참고문헌

[1] Huang, Hsin-Yuan, et al. “Learning shallow quantum circuits.” arXiv preprint arXiv:2401.10095 (2024). [2] https://pennylane.ai/qml/demos/tutorial_learningshallow/

[참고문헌 1]이 1월 18일에 게제된 원 논문, [참고문헌 2]는 해당 논문의 내용을 기반으로 제 3자가 1월 24일에 작성한 설명글이다.