IMO 조합 문제를 DP로 풀어보자
저번 글에 이어 이번에도 IMO(국제 수학 올림피아드)와 관련된 주제를 가져왔습니다. 오늘은 아마도 이 글을 읽는 분들이 가장 익숙하실 조합 문제들을 다뤄보려고 합니다. 최근 들어 PS에서 다루는 다양한 알고리즘적 사고를 요구하는 문제들이 수학 올림피아드에도 출제되고 있습니다. 특히 DP(점화식)를 이용하는 문제가 최근 2년 연속 IMO에 출제되며 큰 관심을 끌었습니다. 이번 글에서는 이 두 문제의 풀이를 간단히 소개해보려 합니다.
IMO 2022 P6
양의 정수 $n$이 있다. 노르딕 사각형이란 $n\times n$ 모양의 판으로 각 칸에 $1$부터 $n^2$까지의 수가 하나씩 써져있다. 두 개의 칸이 인접하다는 것은, 두 칸이 한 변을 공유하는 경우를 뜻한다. 어떤 칸이 골짜기인 것은 이 칸과 인접한 칸에 적힌 수들이 이 칸의 숫자보다 모두 큰 칸을 뜻한다. 이제 다음 세 조건을 만족하는 칸들의 경로를 오르막길 경로라 하자:
(1) 시작칸은 골짜기이다.
(2) 오르막길 경로는 인접한 칸들을 따라 이동한다.
(3) 오르막길 경로에 적힌 수들은 증가 수열을 이룬다.
이때, 노르딕 사각형에 있는 오르막길 경로의 개수의 최솟값을 $n$에 대한 함수로 표현하여라.
문제를 읽어보니 뭔가 익숙한 그림이군요… BOJ 1937 욕심쟁이 판다
위 문제는 다음과 같이 DP로 해결 가능합니다. 편의상 이 문제에서도 $1$부터 $n^2$까지의 수가 쓰여 있다고 생각합시다. $i$가 적힌 칸에 도달하는 경로의 최대 길이 $dp[i]$는 다음과 같습니다.
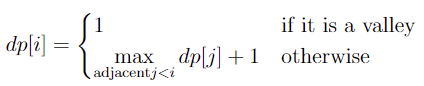
즉, 작은 수부터 보며 인접한 칸 중 자신보다 작은 칸의 점화식 값을 통해 계산할 수 있습니다.
본 문제에서는 경로의 개수를 물어봤으므로, 최댓값이 합으로 바뀝니다.
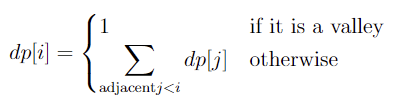
이때 구해야 하는 것은 $\displaystyle\sum_{i=1}^{n^2} dp[i]$ 의 최솟값입니다.
그런데 사실, 이 상태에서 딱히 의미 있는 결과를 도출하기는 어렵습니다. 무엇보다 수들의 배치를 전혀 모르기 때문에 $dp$ 값에 대해서도 추론할 수 있는 정보가 전혀 없습니다. 그래서 규칙을 찾아보고자, $n=3$일 때 여러 가지 경우를 그려보았습니다.
이와 같이 작은 경우에 대해 전수 탐색을 하며 답을 유추하는 과정은 조합 문제를 풀 때 필수적인 과정 중 하나입니다. 그런데 이 경우 전수 탐색을 하기에는, $1$부터 $9$까지의 수를 재배열하는 방법이 너무 많습니다. 여기서 $dp$식 사고가 진가를 발휘합니다. 표에 랜덤하게 수를 적고 $dp$ 값을 계산하다 보면, 어떤 상황에서 최적일지를 보다 쉽게 찾을 수 있습니다. (그리고 무엇보다 시각적으로도 편합니다)
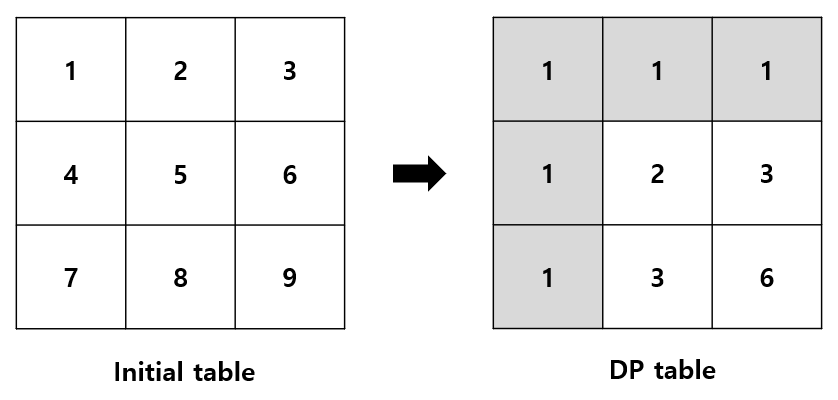
모든 골짜기에 $1$을 쓰고 점화식을 계산하다 보면 골짜기가 아닌데도 $1$이 쓰이는 칸들이 있습니다. 이 칸들은 인접한 칸 중 자신보다 적은 수가 하나밖에 없어 그대로 $1$이 적힌 것입니다. 참고로 $1$이 전파되는 경로를 그려보면 하나의 수형도를 이루게 됩니다. 그리고 남은 칸들은 여러 개의 수들이 합쳐져 $1$보다 큰 값이 쓰이게 됩니다. 이때 핵심은 다음과 같습니다. 전체 합을 최소화하려면 $1$을 최대한 많이 사용하고, 점화식의 중첩을 최소화해야 합니다. 여기서 중첩이란 다음을 의미합니다.
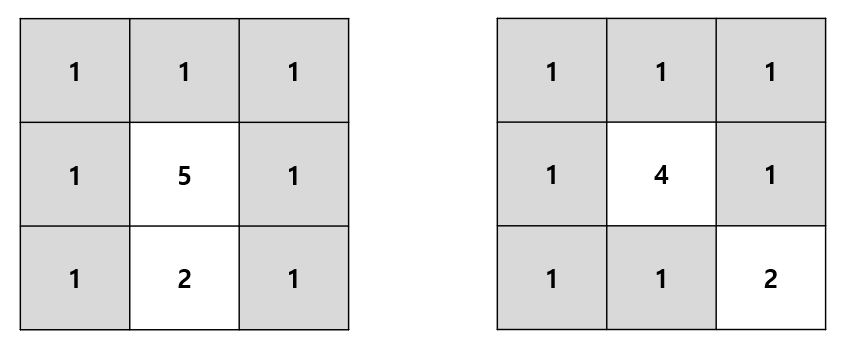
위 두 경우를 비교해보면, 전체 합은 왼쪽이 오른쪽보다 $1$만큼 더 큽니다. 이런 차이가 발생한 것은, 왼쪽 그림에서 $1$들의 합으로 계산된 $2$가 가운데 칸을 계산하는데 한 번 더 사용되었기 때문입니다. 이를 바탕으로 생각해보면, 다음과 같은 상황이 최적이기를 기대해볼 수 있습니다.
최대한 1들로 채워 남은 칸들이 서로 인접하지 않게 한다
다행히도, 이것이 실제로 가능합니다! 실례 찾기는 여러분에게 맡기겠습니다. 이떄의 답은 $2n^2-2n+1$입니다.
실례
이런 형태를 유지하며 회색을 칠하고, 회색 칸들에 $1$이 오도록 수를 배치하면 됩니다. 참고로 이때의 답이 $2n^2-2n+1$이라는 것은 이후의 증명 과정이 보장해줍니다.
참고로 지금까지의 내용들은 모두 관찰입니다. 즉, 엄밀한 추론 근거가 있지 않지만, 다양한 접근을 통해 그럴 확률이 높다고 생각되는 내용들을 써 내려간 것입니다. 당연히 틀릴 수도 있습니다. 그러나 이런 류의 직관은 문제를 빠르게 이해하고 풀이를 찾아내는데 큰 도움을 줍니다. 더불어, 이런 직관이 직접적으로 풀이로 이어지는 경우도 있습니다.
위 직관이 실제로 맞는지 확인하려면, 임의의 상황에 대한 엄밀한 계산이 필요합니다. 그대로 따라해봅시다!
먼저 $dp$ 값이 $1$보다 큰 칸들에 대해, 이 칸들은 주위 칸들에 대한 점화식 값의 합으로 표현됩니다. 우리는 그 칸들이 전부 $1$이기를 바랍니다. 그러니 이런 식으로 접근해봅시다. $i$ 주위의 칸들 중 적힌 수가 $i$보다 작은 칸의 개수를 $d_i$라 하면, 당연히 $dp[i]\geq d_i$ 가 성립합니다.
\[\sum_{i=1}^{n^2}dp[i]= n^2+\sum_{dp[i]>1}(dp[i]-1)\geq n^2 +\sum_{dp[i]>1}(d_i-1)\]그럼 $d_i$들의 합은 어떻게 알 수 있을까요? 각 칸들을 점으로 생각하여 인접한 칸끼리 변으로 이으면, $d_i$는 이 그래프에서 일종의 차수의 역할을 합니다. 이 그래프에서 $dp[i]>1$인 모든 칸들을 큰 수부터 지워 나간다고 생각하면, 매 차례마다 $d_i$개의 변이 사라질 것입니다. 이때 남은 그래프는 위에서 언급했듯 수형도(forest)를 이룹니다. 그 이유는, 남은 간선들에 대해 큰 수에서 작은 수로 방향을 부여하면 모든 점의 outdegree가 $1$ 이하인 DAG가 되기 때문입니다. Forest의 점과 변 개수를 각각 $v$와 $e$라 하면, 위 합을 정확히 계산할 수 있습니다.
\[\sum_{dp[i]>1}(d_i-1)=\sum_{dp[i]>1}d_i-\sum_{dp[i]>1}1=(2n(n-1)-e)-(n^2-v)\]이때 $2n(n-1)$은 원래 그래프의 변 개수입니다. 따라서 $v-e=\text{(number of components)}\geq 1$ 인 forest의 특징을 이용하면
\[\sum_{i=1}^{n^2} dp[i]\geq 2n(n-1)+(v-e)\geq 2n^2-2n+1\]가 성립합니다. $\blacksquare$
위에서 제시한 실례는 이 등호조건들을 모두 만족하므로, 그때의 답은 $2n^2-2n+1$일 수 밖에 없습니다.
사실 이 문제를 푸는 데 있어 $dp$ 점화식의 특별한 성질이 사용되진 않습니다. 실제로 $dp$를 전혀 사용하지 않고도 문제를 쉽게 해결할 수 있습니다. 그러나 제가 $dp$를 이용한 풀이를 소개한 것은, 실제로 점화식을 계산해보면서 문제에 대한 직관을 쉽게 터득할 수 있기 때문입니다. 이 문제는 특히 실례 찾기가 어려운 편인데, $dp$를 이용한 풀이는 해당 실례에 대한 정당성과 동시에 실제 풀이의 방향도 제시해줍니다.
실제 통계: 평균 $0.683$점, 만점자는 $22/589$.
IMO 2023 P5
양의 정수 $n$이 있다. 일본 삼각형 이란 $1+2+\cdots+n$개의 원들이 정삼각형 형태로 배열된 도형으로, $i=1,2,\cdots,n$에 대해 $i$번째 행에는 정확히 $i$개의 원이 있고, 그 중 정확히 하나의 원이 빨간색으로 칠해져 있다. 일본 삼각형의 닌자 경로란 $n$개의 원으로 이루어진 경로로, $1$행에서 시작해 바로 아래에 인접한 두 개의 칸들 중 하나를 고르는 과정을 반복해 마지막 행까지 진행한다. 아래 그림은 $n=6$인 일본 삼각형의 예시로, 주어진 닌자 경로는 2개의 빨간 원을 지난다.
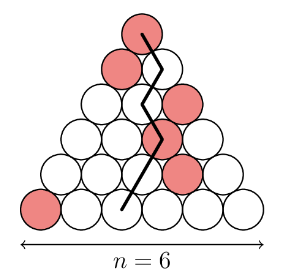
이때 임의의 일본 삼각형에서 $k$개 이상의 빨간 원을 지나는 닌자 경로가 존재하는 정수 $k$의 최댓값을 $n$에 대한 함수로 표현하여라.
마찬가지로 익숙한 그림입니다. BOJ 1932 정수 삼각형
이 문제를 풀던 방법을 떠올려보면, 이차원 dp 배열을 정의해 문제를 해결합니다. 이때 사용한 정의는 대략 다음과 같습니다.
$dp[i][j]$ : 맨 위 칸에서 $i$행 $j$번째 칸으로 이동하는 경로들에 대해 선택된 수들의 합의 최댓값
이때의 점화식은 대략 다음과 같습니다.
\[dp[i][j]=\max(dp[i-1][j-1], dp[i-1][j])+(\textbf{value at (i, j)})\]일본 삼각형에서도 완전히 동일한 점화식을 정의할 수 있습니다. 이때 구하는 값은 경로가 지나는 빨간색 원의 개수가 될 것입니다.
$a[i][j]$ : 맨 위 원에서 $i$행 $j$번째 원으로 이동하는 경로들에 대해 지나는 빨간색 원의 개수의 최댓값
이때의 점화식은 다음과 같습니다. ($i$행 $j$번째 칸의 빨간색 여부를 $r[i][j]$로 표기합시다)
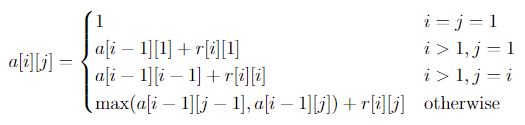
PS 문제였다면 이를 단순히 계산하고 끝이겠지만, 이 문제는 수학 문제이므로 해당 점화식이 가질 수 있는 값들을 수학적으로 분석해야 합니다. 우리의 목표, $k$개 이상의 빨간 원을 지나는 닌자 경로가 존재하는 것은 다음과 정확히 동치입니다.
\[\max_{1\leq j\leq n} a[n][j] \geq k\]즉, 우리는 각 행에서 최댓값들의 성질을 찾아볼 필요가 있습니다. 다만, 우리는 각 행에서 빨간색 원의 위치를 정확하게 알지는 못합니다. 그러니 일단은 각 행에 있는 항들의 합을 살펴봅시다. 각 행에는 정확히 한 개의 빨간 원만 있으므로, 각 행에 대해 위 점화식을 모두 더하면 $r$ 항이 사라질 것입니다.
$i(>1)$ 행의 합을 $S_i$, 최댓값을 $M_i$라 하고, $i-1$행에서 최댓값이 $k$번째에 있다고 가정하면, 위 점화식을 이용하면 다음과 같이 식을 세울 수 있습니다.
\[S_i = \sum_{j=1}^i a[i][j]=a[i-1][1]+\sum_{j=2}^{i-1} \max(a[i-1][j-1], a[i-1][j])+a[i-1][i-1] +1\] \[\geq \sum_{j=1}^k a[i-1][j]+\sum_{j=k}^{i-1} a[i-1][j]+1=S_{i-1}+a[i-1][k]+1=S_{i-1}+M_{i-1}+1\]두 번째 줄의 부등식은 아래 그림에 의해 성립합니다.
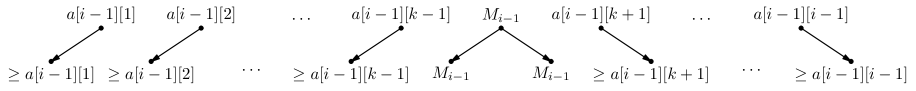
이때 비둘기집의 원리에 의해 $M_i\geq \left\lceil\displaystyle\frac{1}{i}S_i\right\rceil$ 이므로, $S_i$에 대한 점화식을 얻을 수 있습니다.
\[S_i\geq S_{i-1}+\left\lceil{\frac{S_{i-1}}{i-1}}\right\rceil+1(i\geq 2), S_1=1\]이를 순차적으로 계산해보면 $S_i$에 대한 하한을 계산할 수 있고, 마찬가지로 $M_i$의 하한 또한 구할 수 있습니다. 실제로 정확한 계산값을 귀납적으로 보일 수 있습니다.(자세한 계산은 여러분께 맡깁니다)
구체적으로, $i=2^k-r(1\leq r\leq 2^{k-1})$ 꼴일 때 $S_i=k\times i-r+1$ 로 구해집니다.
따라서 $M_i\geq \left\lceil\displaystyle\frac{1}{i}S_i\right\rceil =k=\lfloor \log_2 n\rfloor+1$ 임을 알 수 있습니다. 실제로 이 값이 답이고, 이에 대한 실례 또한 찾을 수 있습니다.
실례
어떤 한 빨간 원에서 다른 빨간 원으로 가는 경로가 존재한다는 것은, 한 원을 꼭짓점으로 하는 정삼각형 그림자 내에 다른 원이 포함된다는 뜻입니다. 이러한 현상이 최대한 덜 일어나도록 빨간 원들을 배치하면 됩니다. 이에 대한 최적의 배치는, 체스의 나이트와 같이 두 칸씩 뛰며 빨간 원을 배치하는 것입니다.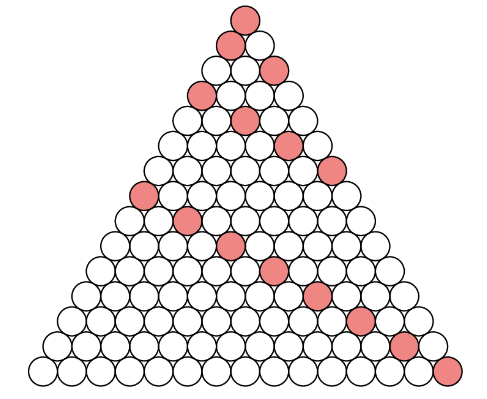
위 증명 과정을 통해서도 유추가 가능합니다. 위 부등식의 등호 조건을 만족시키려면, 각 행의 최댓값이 거의 평균에 가깝기 때문에 각 행의 원소들이 모두 비슷한 값을 가져야 합니다. 위 실례에 대해 점화식을 계산해보면 두 칸씩 뛰며 색칠하는 방식이 $S_i$를 가장 적게 증가시킨다는 것을 알 수 있습니다. $\blacksquare$
이 문제는 위 문제와 달리 DP 점화식의 성질을 직접적으로 활용하였습니다. 각 행의 점화식들을 연립하여 대수적으로 하한을 구하는 문제였습니다.
PS1. $M_i$의 하한을 훨씬 간단히 구할 수 있는 방법이 있습니다. 위 아이디어를 활용하여 다음 사실을 증명해보세요!
\[\sum_{j=1}^i \frac{1}{2^{a[i][j]}}< 1\]PS2. 참고로 이 문제는 매우 짧은 풀이가 존재합니다. 이 또한 PS적인 사고를 요구하니 한 번 고민해보세요!
힌트
트리풀이
주어진 일본 삼각형에서 인접한 행끼리 변들로 이어 트리를 그리려 합니다. 방법은 다음과 같습니다. 귀납적으로 $i$행까지 트리가 그려졌을 때, $i$행의 빨간색 원을 기준으로 다음과 같이 변을 추가합니다. 빨간색 원 왼쪽의 원들은 왼쪽 아래의 원과 연결하고, 빨간색 원 오른쪽의 원들은 오른쪽 아래의 원과 연결합니다. 빨간색 원은 아래 두 원과 모두 연결합니다. 이를 반복하면 가상의 $n+1$행까지 이어 그래프를 만들 수 있습니다. 이 그래프는 거시적으로 보면 하나의 이진 트리이며, 리프가 $n+1$개 입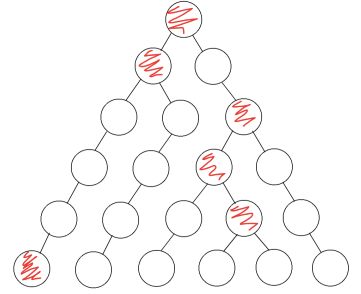니다.
높이가 $h$인 이진 트리는 리프가 최대 $2^h$개이며, 거꾸로 리프가 $m$개인 이진 트리의 높이는 최소 $\lceil \log_2 m \rceil $입니다. 즉 이 트리의 높이는 최소 $\lceil \log_2 (n+1) \rceil=\lfloor \log_2 n \rfloor+1$입니다. 트리의 construction을 보면 빨간색 원을 만날 때마다 분기가 일어나기 때문에, 이는 곧 빨간색 원을 트리의 높이만큼 지날 수 있음을 뜻합니다. $\blacksquare$
그리디적인 사고를 이용하면 위 아이디어를 훨씬 간단하게 서술할 수 있습니다. 이진 트리의 꼭짓점에서 시작하여 내려오는데, 분기점을 만날 때마다 두 길 중 남은 빨간색 원이 더 많은 쪽으로 이동합니다. 매번 빨간색 원의 개수가 절반 이하로 줄기 때문에 증명이 됩니다.
실제 통계: 평균 $2.417$점, 만점자는 $118/618$.
Summary
2년 동안 IMO에 출제된 DP 문제들을 풀어보았습니다. 문제를 보시면 알겠지만, 문제 상황 자체는 PS를 어느 정도 경험하신 분들이라면 충분히 친숙한 상황입니다. 물론 위 문제들은 그 점화식을 바탕으로 대수적인 연립 과정이나 하한을 추측하는 등 추가적인 아이디어들을 요구합니다. 위 문제들을 어떻게 느끼실지는 모르겠지만, 우리들에게 친숙한 DP 문제들이 이런 식으로도 활용될 수 있다는 사실을 알려드리고자 이 글을 작성하였습니다. 이 외에도 재미있는 조합 문제들이 많으니, 심심할 때 한 번 풀어보시면 좋을 것 같습니다.