Introduction
이 글에서는 Block Decomposition을 이용한 Online FFT(Fast Fourier Transform) 구현 방법을 소개합니다.
두 수열 $A$, $B$의 convolution $C$를 $\mathcal{O}(n\log n)$에 구하는 FFT 알고리즘은 두 수열 $A$, $B$가 모두 주어져야만 사용할 수 있습니다. Online FFT는 $A$, $B$의 원소 $a_i$, $b_i$가 하나씩 주어질 때 $c_i$를 온라인으로 구하는 알고리즘입니다. 이는 점화식이 convolution 형태이면서 $c_0, \cdots, c_{i-1}$을 알아야 $a_i$, $b_i$를 구할 수 있는 경우(예를 들면 카탈란 수 $C_{n+1} = \sum_{i=0}^n C_i C_{n-i}$)에 사용할 수 있습니다.
Online FFT는 여러 구현 방법이 있으며, 그중 가장 잘 알려진 방법은 분할 정복을 이용하는 $\mathcal{O}(n\log^2 n)$ 기법입니다. 이에 대해선 이미 좋은 글(링크)이 있으니, 일독을 권합니다. 다른 방법은 블록 단위로 2차원 grid를 분해해서 convolution을 구하는 기법이 있습니다. 첫 번째 방법은 비교적 잘 알려진 거 같지만, 두 번째 방법을 소개하는 글은 많이 못 본 거 같아서 글을 써봅니다.
Formulation
일반적인 FFT 문제는 다음과 같이 정의됩니다.
- $A = { a_0, \cdots, a_n }$, $B = { b_0, \cdots, b_m }$이 주어질 때 $c_k = \sum_{i+j=k}{a_i b_j}$로 정의되는 수열 $C = { c_0, \cdots, c_{n + m} }$를 구해라.
비슷하게, Online FFT 문제는 다음과 같이 정의됩니다.
- $k = 0, 1, \cdots$에 대해 $a_k$, $b_k$가 주어질 때 $c_i = \sum_{i+j=k}{a_i b_j}$를 구해라.
일반적인 FFT의 구현 방법인 Cooley-Tukey Algorithm은 $A$, $B$의 짝수항과 홀수항을 나눠 분할 정복을 하는 방식이기에 수열 $A$, $B$를 처음부터 알고 있어야 $C$를 계산할 수 있습니다. 따라서 Online FFT 문제를 해결하기 위해서는 다른 접근법이 필요합니다.
Online FFT - $\mathcal{O}(n\sqrt{n\log n})$ using Sqrt Decomposition
(다음 글을 바탕으로 작성되었습니다. https://codeforces.com/blog/entry/59452)
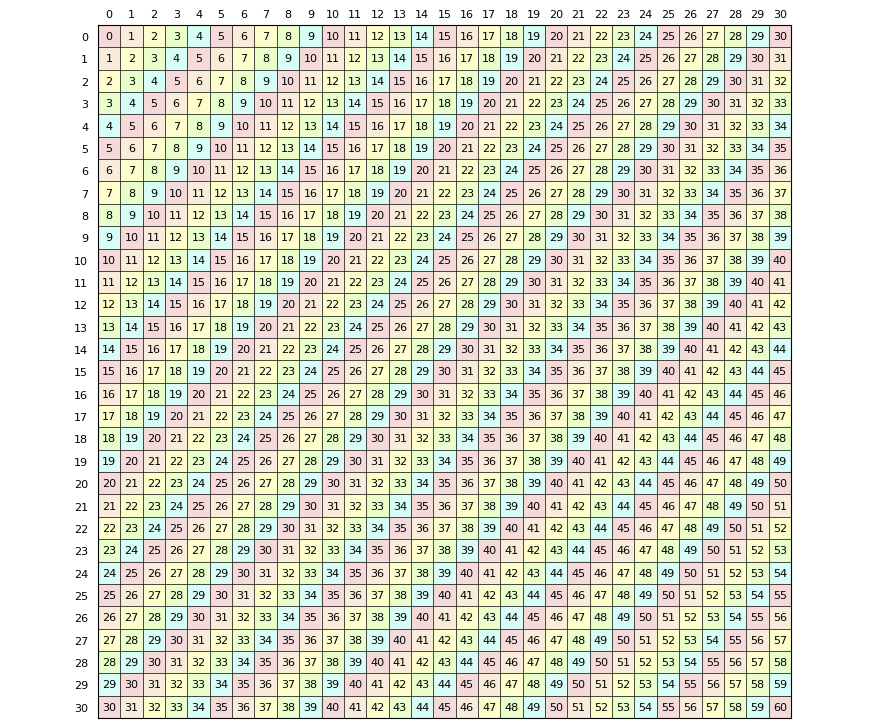
$[0, n] \times [0, n]$ 그리드 위의 $(i, j)$에 $a_i b_j$가 쓰여있다고 가정합시다. $c_k$를 구하는 건 $i + j = k$인 $(i, j)$로 이루어진 대각선의 합을 구하는 것과 같습니다.
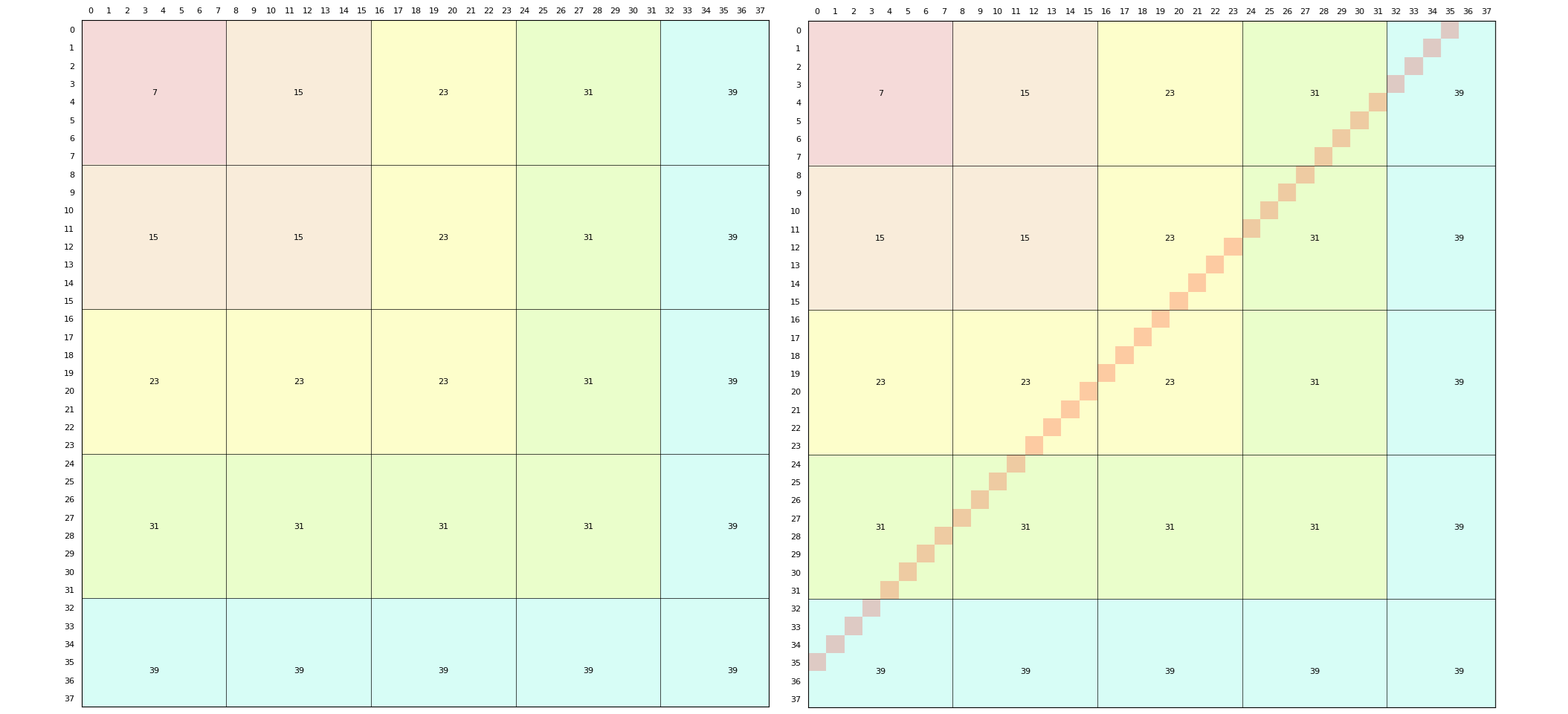
이제 그리드를 $B \times B$ 크기의 블록으로 분할해, 일종의 Sqrt Decomposition으로 대각선의 합을 빠르게 계산하는 방법을 알아보겠습니다. 각 블록 $T_{i,j} = [iB, iB + B - 1] \times [jB, jB + B - 1]$을 이용하면 $[0, n] \times [0, n]$ 그리드를 $\mathcal{O}((\frac{n}{B})^2)$개의 영역으로 나눌 수 있고, $T_{i,j}$의 convolution을 구해 누적하면 대각선상의 합을 빠르게 구할 수 있습니다.
각 블록의 모든 값이 주어질 때마다 $a_{iB}, \cdots, a_{iB + B - 1}$과 $b_{jB}, \cdots, b_{jB + B - 1}$의 convolution을 계산하여 $c_{(i + j)B}, \cdots, c_{(i + j)B + 2B - 2}$에 누적한다고 합시다. 이렇게 하면 $c_k$를 구할 때 $i + j = k$를 만족하는 $(i, j)$ 중 일부만 아직 반영되지 않았고, 나머지는 이미 convolution을 통해 추가된 상태일 것입니다. 이때 반영되지 않은 $(i, j)$의 개수는 $\mathcal{O}(B)$개이니, 직접 계산하며 $c_k$를 구할 수 있습니다. 예를 들어 Fig.2 처럼 $B = 8$인 경우, $c_{35}$를 구할 땐 파란색 영역의 $4 + 4 = 8$개의 값만 직접 계산을 하면 됩니다.
이를 이용하면 Online FFT를 $\mathcal{O}((\frac{n}{B})^2 B\log B + nB)$에 구할 수 있습니다. 여기서 $B = \sqrt{n\log n}$으로 설정하면 $\mathcal{O}(n\sqrt{n \log n})$의 시간복잡도를 얻습니다.
구현 코드는 다음과 같습니다.
template<int mod, int g>
auto conv(auto a, auto b) {
// O(n\log n) convolution using fft
}
template<int mod, int g, int k = 8000>
struct online_fft {
void push(int an, int bn) {
const int n = a.size();
const int m = n / k;
a.push_back(an);
b.push_back(bn);
if ((n + 1) % k) return;
auto update = [&](int i, int j) {
vector ca(a.begin() + i, a.begin() + i + k);
vector cb(b.begin() + j, b.begin() + j + k);
vector f = conv<mod, g>(ca, cb);
for (int x = 0; x < 2 * k - 1; x++) {
c[i + j + x] = c[i + j + x] + f[x];
if (c[i + j + x] >= mod) c[i + j + x] -= mod;
}
};
c.resize(2 * n + 1);
for (int i = 0; i <= m; i++) {
update(i * k, m * k);
if (i < m) update(m * k, i * k);
}
}
int get(int n) const {
if (n < a.size() / k * k) return c[n];
if (n < k) {
int ret = 0;
for (int i = 0; i <= n; i++) {
ret = (ret + 1LL * a[i] * b[n - i]) % mod;
}
return ret;
}
else {
int ret = c[n];
for (int i = 0; i < (n + 1) % k; i++) {
ret = (ret + 1LL * a[i] * b[n - i]) % mod;
ret = (ret + 1LL * a[n - i] * b[i]) % mod;
}
return ret;
}
}
private:
vector<int> a, b, c;
};
뒤의 Benchmarking에서 알아보겠지만, 실제 구현에서는 convolution의 오버헤드를 고려해 이론적 최적값인 $B = \sqrt{n\log n}$보다 약간 큰 $B = 8\,000$을 이용하는 게 더 효율적입니다.
다음은 해당 방법으로 BOJ 1067번 문제를 해결하는 코드입니다: http://boj.kr/08268a376d8443b69657e9806177b316
Online FFT - $\mathcal{O}(n\sqrt{n})$ using Sqrt Decomposition
(다음 글을 바탕으로 작성되었습니다. https://www.acmicpc.net/blog/view/122)
Online FFT의 $\mathcal{O}((\frac{n}{B})^2 B\log B + nB) = \mathcal{O}(n\sqrt{n\log n})$ 구현에서 Fourier Transform의 성질을 잘 이용하면 DFT(Discrete Fourier Transform), IDFT(Inverse Discrete Fourier Transform)의 횟수를 줄일 수 있습니다.
두 수열 $A$, $B$의 DFT를 각각 $\mathcal{F}(A)$, $\mathcal{F}(B)$라 하고, $\mathcal{F}(A + B) = \mathcal{F}(A) \times \mathcal{F}(B)$가 성립합니다. 이때 $+$는 element-wise sum을, $\times$는 element-wise product를 의미합니다. 이를 이용하면 $a_{iB}, \cdots, a_{iB + B - 1}$과 $b_{jB}, \cdots, b_{jB + B - 1}$의 DFT를 저장한 뒤, 각각 곱해서 누적하고 한 번에 IDFT를 적용하는 방식으로 DFT, IDFT의 횟수를 $\mathcal{O}(\frac{n}{B})$번으로 줄일 수 있습니다.
시간복잡도는 DFT, IDFT의 계산에 $\mathcal{O}(\frac{n}{B}B\log B)$, $\mathcal{F}(A) \times \mathcal{F}(B)$를 계산하고 누적하는데 $\mathcal{O}((\frac{n}{B})^2 B)$, 반영되지 않은 값을 계산하는데 $\mathcal{O}(nB)$의 연산량이 필요하니 $\mathcal{O}(n\log B + \frac{n^2}{B} + nB)$이고, $B = \sqrt{n}$일 때 $\mathcal{O}(n\sqrt{n})$이 됩니다.
구현 코드는 다음과 같습니다.
template<int mod, int g, int k = 1 << 9>
struct online_fft {
online_fft() : c(k) {}
void push(int an, int bn) {
const int n = a.size(), m = n / k;
a.push_back(an);
b.push_back(bn);
if (n < k || (n + 1) % k) return;
auto calc = [&](const auto& v, auto& fv) {
fv.push_back(vector(2 * k, 0));
copy(v.end() - k, v.end(), fv.back().begin());
ntt(fv.back(), 0);
};
auto update = [&](int i, int j) {
for (int x = 0; x < 2 * k; x++) {
int val = mul(fa[i - 1][x], fb[j - 1][x]);
fc[i + j - 1][x] = add(fc[i + j - 1][x], val);
}
};
calc(a, fa);
calc(b, fb);
fc.resize(2 * m, vector(2 * k, 0));
for (int i = 1; i <= m; i++) {
update(i, m);
if (i < m) update(m, i);
}
ntt(fc[m], 1);
c.resize(n + 2 * k);
for (int x = 0; x < 2 * k - 1; x++) {
c[n + x + 1] = add(c[n + x + 1], fc[m][x]);
}
}
int get(int n) {
if (n < 2 * k) {
int ret = 0;
for (int i = 0; i <= n; i++) {
ret = add(ret, mul(a[i], b[n - i]));
}
return ret;
}
else {
int ret = c[n];
for (int i = 0; i < k; i++) {
ret = add(ret, mul(a[i], b[n - i]));
ret = add(ret, mul(a[n - i], b[i]));
}
return ret;
}
}
private:
int add(int a, int b) { return a + b < mod ? a + b : a + b - mod; }
int mul(int a, int b) { return 1LL * a * b % mod; }
void ntt(auto& f, bool inv) {
// O(n\log n) fft implementation
};
private:
vector<int> a, b, c;
vector<vector<int>> fa, fb, fc;
};
다음은 해당 방법으로 BOJ 1067번 문제를 해결하는 코드입니다: http://boj.kr/75793bd3363e4a65a58f216742988779
Online FFT - $\mathcal{O}(n\log^2{n})$ using Block Decomposition
(다음 글을 바탕으로 작성되었습니다. https://qiita.com/Kiri8128/items/1738d5403764a0e26b4c#fn-siki)
이번엔 고정된 $B \times B$ 크기의 블록을 이용하는 대신, 크기가 $2$배씩 커지는 재귀적인 구조를 이용해 블록 단위로 convolution을 누적하며 $c_k$를 구하는 방법을 알아봅시다.
![Fig.3 Block Decomposition, val([l1, r1] * [l2, r2]) = max(r1, r2)](/assets/images/2025-03-23-online-fft/fig3.png)
Fig.3 과 같이 한 변의 길이가 $1, 2, \cdots, 2^k$인 정사각 영역으로 그리드를 분할합시다. 이렇게 그리드를 분할하면 $i + j = k$인 $(i, j)$를 포함하는 블록 $[l_1, l_2] \times [r_1, r_2]$에서 $\max(l_2, r_2) \leq k$가 성립합니다. 증명은 분할 방법의 재귀적 구조를 이용하면 가능합니다.
위의 사실에 의해 $c_k$를 구하는 시점에 필요한 값이 포함된 블록은 이미 convolution을 계산한 뒤입니다. 따라서 각 블록의 값이 모두 주어지는 시점에 convolution을 계산해 누적할 수만 있다면 $c_k$를 바로 구할 수 있습니다. 이를 위해 블록을 순회하는 방법을 알아봅시다.
$a_i$, $b_i$가 주어지는 시점에 모든 값이 주어지는 블록을 찾아 순회하는 방법은 ${ 0 } / { 1, 2 } / { 3, 4, 5, 6 } / { 7, 8, 9, 10, 11, 12, 13, 14 } / \cdots$ 단위로 구간을 나눈 뒤 각 구간에서 규칙을 구하면 찾을 수 있습니다. $i$가 속하는 구간의 길이를 $s$라 하면, $s = 2^{\lfloor \log_2(i + 1) \rfloor}$가 성립합니다. 또한 $i$가 구간에서 $k$번째 값이라 하면, 업데이트해야 하는 블록은 $t =$ __builtin_ctz(k)에 대해 $(0, i)$에서 아래로 내려가면서 만나는 변의 길이가 $1, 2, \cdots, 2^t$인 블록들과 그 블록의 $y = x$ 대칭 위치에 있는 블록입니다.
시간복잡도는 길이가 $s$인 블록의 개수가 $\mathcal{O}(\frac{n}{s})$개이고, 각 블록의 convolution을 구해 누적하는 연산량이 $\mathcal{O}(s\log s)$이니 $\mathcal{O}(\sum(\frac{n}{s})s\log s) = \mathcal{O}(n\log^2 n)$입니다.
구현 코드는 다음과 같습니다.
template<int mod, int g>
auto conv(auto a, auto b) {
// O(n\log n) convolution using fft
}
template<int mod, int g>
struct online_fft {
void push(int an, int bn) {
const int n = a.size();
const int s = __lg(n + 1);
const int k = __builtin_ctz(n + 2 - (1 << s));
a.push_back(an);
b.push_back(bn);
auto update = [&](int x, int y, int sz) {
vector ca(a.begin() + x, a.begin() + x + sz);
vector cb(b.begin() + y, b.begin() + y + sz);
vector f = conv<mod, g>(ca, cb);
for (int i = 0; i < f.size(); i++) {
if (c.size() <= x + y + i) c.push_back(0);
c[x + y + i] += f[i];
if (c[x + y + i] >= mod) c[x + y + i] -= mod;
}
};
for (int x = n, y = 0, i = 0; i <= k; i++) {
update(x, y, 1 << i);
if (x != y) update(y, x, 1 << i);
x -= 1 << i;
y += 1 << i;
}
}
int get(int n) const {
return c[n];
}
private:
vector<int> a, b, c;
};
다음은 해당 방법으로 BOJ 1067번 문제를 해결하는 코드입니다: http://boj.kr/cb17b208dd074222863ac96c99684ddc
Online FFT - $\mathcal{O}(n\log^2 n)$ using DnC
마지막으로 이번 글의 메인 주제는 아니지만, 지금까지 소개한 방법과의 성능 비교를 위해 일반적으로 알려진 분할 정복을 이용한 Online FFT의 $\mathcal{O}(n\log^2 n)$ 구현을 간략히 소개합니다.
$[l, r]$ 구간의 $c_k$ 값을 구할 때 $[l, m]$ 범위를 재귀 호출해 해당 범위의 $a_i$, $b_i$ 값을 구했다면, 해당 값이 $c_{m+1}, \cdots, c_r$에 미치는 영향력을 계산한 뒤 $[m + 1, r]$ 범위를 재귀 호출하며 남은 값을 계산할 수 있습니다. 이때 영향력은 $\mathcal{O}((r - l)\log(r - l))$에 계산할 수 있으니, $T(n) = 2T(n / 2) + \mathcal{O}(n\log n) = \mathcal{O}(n\log^2 n)$에 Online FFT를 구현할 수 있습니다.
다음은 해당 방법으로 BOJ 1067번 문제를 해결하는 코드입니다: http://boj.kr/6236c31b484843549c119a95aaa0cb75
Benchmarking
Fig.4 는 $n = 1, \cdots, 10^6$ 범위에서 각 Online FFT 구현 방식의 수행 시간을 측정한 결과입니다.
naive: Naive한 $\mathcal{O}(n^2)$ 구현, $n = 10^4$ 이상부터 급격히 성능 저하sqrtlog: Sqrt Decomposition 기반 $\mathcal{O}(n\sqrt{n\log n})$ 구현. ($B = 6\,000, 8\,000, 10\,000$)sqrt: Sqrt Decomposition 기반 $\mathcal{O}(n\sqrt n)$ 구현. ($B = 2^9, 2^{10}, 2^{11}$)logsquare: Block Decomposition 기반 $\mathcal{O}(n\log^2 n)$ 구현.logsquare_dnc: DnC 기반 $\mathcal{O}(n\log^2 n)$ 구현.
측정 결과를 보면 $n$이 커짐에 따라 알고리즘의 수행 시간이 실제 시간복잡도에 따라 증가함을 알 수 있습니다. 이때 $n$이 $200\,000$ 이하로 작을 땐 sqrt가 logsquare_dnc보다 빠른 것과 같이 Sqrt Decomposition 기반 알고리즘도 충분히 빠른 성능을 보임을 알 수 있습니다.
하지만 전반적으로는 크기를 $2$배씩 키워나가며 Block Decomposition을 하는 Online FFT의 $\mathcal{O}(n\log^2 n)$ 비재귀 구현이 가장 우수한 성능을 보였습니다. 이는 같은 복잡도의 더 잘 알려진 DnC 알고리즘보다 해당 구현이 더 나은 성능을 보임을 시사합니다.
Conclusion
이 글에서는 다양한 Online FFT 구현 방법을 소개하고, 기존의 DnC 기반 Online FFT와 성능을 비교해 보았습니다.
DnC 방식의 Online FFT는 $a_k$, $b_k$가 주어지거나 $c_k$를 구하는 과정에서 블랙박스화하기 어려운 구조를 가지는 반면, Block Decomposition 방식은 이를 보다 쉽게 블랙박스화할 수 있으며, 실제 성능 또한 더 우수함을 확인할 수 있었습니다.
성능 측정에서는 기본적인 형태의 비재귀 NTT 구현을 사용하였으며, 더 나은 성능을 얻기 위해서는 최적화된 FFT/NTT 라이브러리를 활용할 수 있을 것입니다. 예시로 AtCoder Library의 convolution 구현을 이용하면 $n = 500\,000$ scale에서 3000ms 정도에 동작하는 $\mathcal{O}(n\log^2 n)$ 코드를 얻을 수 있습니다. (코드)
FFT 자체가 난도가 있는 주제이기에 Online FFT는 상대적으로 진입 장벽이 높은 편이지만, 기본적인 FFT 개념을 알고 있다면 여기에 몇 가지 아이디어를 조합하여 어렵지 않게 구현할 수 있는 알고리즘입니다. 또한, 최근 ABC 315에서도 출제되는 등 점차 well-known한 유형이 되어가고 있으므로, 관심이 있다면 한 번 공부해 보시기를 추천드립니다.
References
- https://infossm.github.io/blog/2023/09/24/relaxed-convolution/
- https://infossm.github.io/blog/2023/10/24/relaxed-convolution-2/
- https://blog.naver.com/jinhan814/223203500880
- https://codeforces.com/blog/entry/59452
- https://www.acmicpc.net/blog/view/122
- https://qiita.com/Kiri8128/items/1738d5403764a0e26b4c#fn-siki