Graph Degeneracy와 Subgraph Counting

algorithm , graph-theory , problem-solving

1. Introduction

그래프 $G$에서 특정 패턴 그래프 $H$와 동형인 subgraph를 찾거나 그 개수를 계산하는 문제는 알고리즘 대회 뿐만 아니라 여러 분야에서 중요한 주제입니다. 특히 삼각형($C_3$)이나 $4$-사이클($C_4$), 경로($P_k$), 클리크($K_k$) 등 잘 알려진 그래프를 대상으로 한 문제는 이미 많은 문제로 출제된 바가 있습니다.

이번 글에서는 graph degeneracy 개념을 이용해 subgraph counting 문제를 해결하는 일반적인 방법을 소개합니다. 그래프는 무방향 단순 연결 그래프를 대상으로 하며, 이분 그래프(bipartite graph), 평면 그래프(planar graph), 트리(tree) 등 특수한 경우에만 적용 가능한 기법은 제외하였습니다.

2. Preliminaries

subgraph counting 기법을 설명하기에 앞서, 필요한 용어와 개념을 먼저 설명하겠습니다.

2.1 Graph Terminology

무방향 그래프 $G$는 다음 두 집합으로 정의됩니다.

\[\begin{align*} V(G) &= \{ 1, \cdots, |V(G)| \} \\ E(G) &= \{ (u, v) \mid u, v \in V(G) \} \end{align*}\]

이때 $V(G)$를 $G$의 정점 집합, $E(G)$를 $G$의 간선 집합이라 합니다. $(u, v) \in E(G)$는 두 정점 $(u, v)$에 대한 순서 없는 튜플입니다.

단순 그래프(simple graph)란 간선에 중복이 없고, 자기 자신으로 향하는 간선(self-loop)이 없는 무방향 그래프입니다.

그래프 $G$가 연결 그래프(connected graph)라는 건 임의의 두 정점 $u, v \in V(G)$에 대해 $p_0 = u,\;p_k = v,\;(p_i, p_{i+1}) \in E(G)\;(\forall 0 \le i < k)$ 를 만족하는 경로 $p_0, p_1, \cdots, p_k$가 존재함을 의미합니다.

정점 $u$의 이웃 집합은 $N_G(u) = { v \mid (u, v) \in E(G) }$로 정의하며, 이로부터 정점 $u$의 차수 $\operatorname{deg}_G(u) =

N_G(u)

$를 정의할 수 있습니다.

2.2 Graph Isomorphism

두 단순 무방향 그래프 $G$, $G’$의 정점 수가 $n =

V(G)

V(G’)

$로 같다고 가정합시다.

일대일 대응(bijection) $f:V(G) \rightarrow V(G’)$가 존재해서 임의의 두 정점 $u, v \in V(G)$에 대해 $(u, v) \in E(G) \Leftrightarrow (f(u), f(v)) \in E(G')$ 라면, $G$, $G’$는 동형(isomorphic)이라 합니다.

즉, $G$의 정점 번호를 다시 매겨서 $G’$를 만들 수 있다면 $G$, $G’$는 동형입니다.

Fig.1

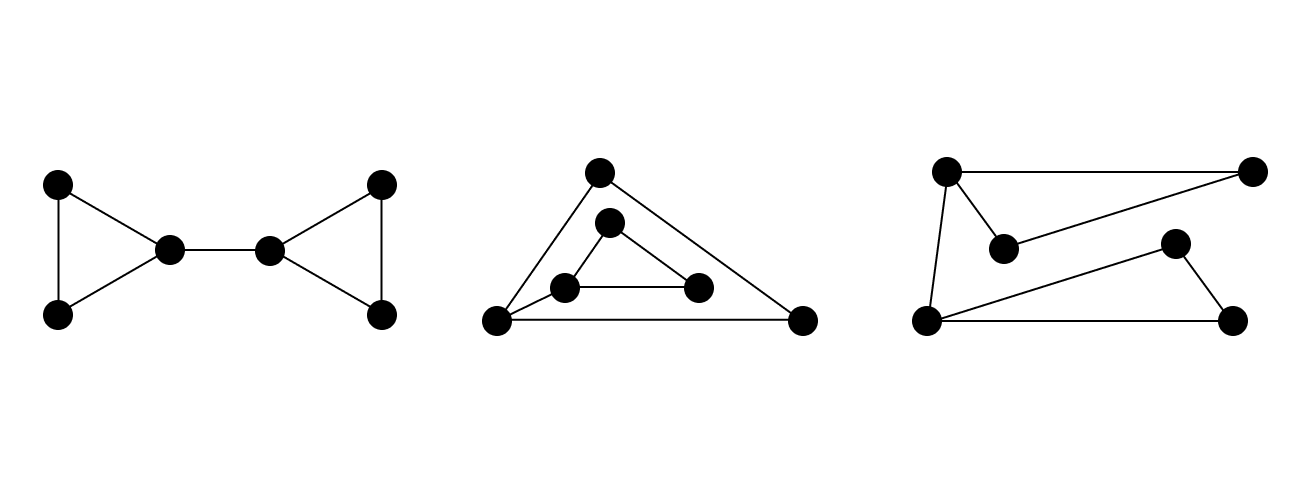
예를 들어 위의 그래프는 모두 동형입니다.

두 그래프가 동형인지 여부를 보이면 그래프가 구조적으로 동일함을 엄밀하게 판별할 수 있습니다.

2.3 Subgraph

무방향 그래프 $G = (V(G), E(G))$에 대해

\[\begin{align*} V' &\subseteq V(G) \\ E' &\subseteq E(G) \end{align*}\]

를 택해서 그래프 $H = (V’, E’)$를 구성할 수 있다면 $H$를 $G$의 subgraph라 하고 $H \subseteq G$라 표기합니다.

두 무방향 그래프 $G, H$가 주어질 때, $G$에 $H$와 동형인 subgraph가 몇 개나 존재하는지 세는 문제를 subgraph counting이라 합니다. 이때 두 subgraph가 정점 집합이나 간선 집합 중 적어도 하나가 다르다면 둘을 다른 subgraph로 구분합니다.

예를 들어 $H$가 세 정점으로 이루어진 단순 사이클 $C_3$라면 $G$에서 삼각형의 개수를 구하는 문제가 되고, 정점이 $4$개인 경로 그래프 $P_4$라면 $G$에서 길이가 $3$인 경로의 개수를 구하는 문제가 됩니다.

2.4 Graph Families

특수한 성질을 갖는 몇 가지 그래프는 subgraph counting 문제에서 패턴 그래프 $H$로 자주 활용됩니다. 주요한 예시는 다음과 같습니다.

경로 그래프($P_n$): $n$개의 정점을 일직선으로 연결하여 $n - 1$개의 간선을 갖는 단순 경로. 두 리프 정점은 차수가 $1$, 나머지 정점은 차수가 $2$이다.
별 그래프($S_n$): $1$개의 중심 정점과 $n - 1$개의 리프 정점을 연결하는 $n - 1$개 간선으로 이루어지는 그래프.
사이클 그래프($C_n$): $n$개의 정점과 $n$개의 간선으로 이루어진 닫힌 경로. 모든 정점의 차수가 $2$이며 하나의 연결 그래프를 형성한다.
클리크($K_n$): $n$개의 정점과 $\frac{n(n-1)}{2}$개의 간선으로 이루어진 단순 연결 무방향 그래프. 모든 정점 쌍이 간선으로 연결되어 있으며 각 정점의 차수는 $n - 1$이다.

$H$가 $C_3, C_4, S_k$ 등의 그래프인 경우에는 subgraph counting 문제를 효율적으로 해결할 수 있음이 알려져 있습니다.

3. Graph Degeneracy

그래프의 degeneracy는 그래프가 얼마나 희소한(sparse) 구조를 가지는지 정량화하는 지표입니다.

3.1 Definition

무방향 그래프 $G$의 degeneracy $d(G)$는 다음과 같이 정의됩니다.

\[d(G) = \max_{H \subseteq G}\min_{v \in V(H)} \operatorname{deg}_H(v)\]

정의에 의해 $G$의 임의의 subgraph $H$에는 항상 차수가 $d(G)$ 이하인 정점이 존재합니다.

예를 들어 트리의 subgraph는 forest이기 때문에 트리는 degeneracy가 항상 $1$이고, 평면 그래프는 $

\le 3

- 6$에서 차수가 $5$ 이하인 정점을 적어도 하나 가지며, 평면 그래프의 subgraph는 평면 그래프이니 degeneracy가 $5$ 이하입니다.

3.2 Degeneracy Ordering

degeneracy ordering은 그래프 $G$에서 차수가 최소인 정점을 제거하는 걸 반복할 때 얻어지는 정점 배열 $L$을 의미합니다.

시작 단계에서 그래프를 $G_0 = G$라 두고, 빈 리스트 $L$을 준비한다.
$i = 0, 1, \cdots, n - 1$에 대해
1. $G_i$에서 차수가 최소인 정점 $v_i$를 선택한다.
2. L의 뒤쪽에 $v_i$를 추가한다.
3. $G_{i+1} = G_i - { v_i }$ (정점 $v_i$와 인접한 간선을 제거)
반복이 끝난 뒤 $L = [v_0, v_1, \cdots, v_{n-1}]$를 얻는다.

이때 $G_i \subseteq G$에서 $\displaystyle \max_i \operatorname{deg}{G_i}(v_i) \le d(G)$가 성립합니다. 또한, 임의의 $H \subseteq G$에 대해 $v_i \in V(H)$인 가장 빠른 $v_i$를 구하면 $H \subseteq G_i$에서 $\operatorname{deg}_H(v_i) \le \operatorname{deg}{G_i}(v_i)$이니, $\displaystyle\min_{u \in V(H)} \operatorname{deg}H(u) \le \operatorname{deg}{G_i}(v_i)$이고 $d(G) \le \displaystyle \max_i \operatorname{deg}_{G_i}(v_i)$가 성립합니다.

따라서 $\max_i \operatorname{deg}_{G_i}(v_i) = d(G)$이고, degeneracy ordering을 이용하면 제거되는 정점의 차수의 최댓값으로 degeneracy를 구할 수 있습니다.

3.3 Property

그래프 $G$의 degeneracy $d(G)$를 $k$라 하면, 어떤 $H \subseteq G$가 존재해서 $k = \min_{v \in V(H)}\operatorname{deg}_H(v)$ 여야 합니다. 이때 $2|E(H)| = \sum_{v \in V(H)}\operatorname{deg}_H(v) \ge k |V(H)| \ge k(k+1)$ 에서 $k(k+1) \le 2|E(G)|$이고, 따라서 $d(G) = \mathcal{O}(\sqrt{|E(G)|})$입니다.

각 정점 $i$에 대해 $(i, j) \in E(G)$이면서 degeneracy ordering에서 $i$보다 $j$가 늦게 등장하는 $(i, j)$ 간선은 최대 $d(G)$개입니다. 위에서 보인 것처럼 그래프의 간선 개수를 $m$이라 할 때 $d(G)$는 $\mathcal{O}(\sqrt m)$에 bound되는 작은 값이니 이 사실을 이용하면 degeneracy ordering을 이용해 효율적으로 문제를 해결할 수 있습니다.

3.4 구현 코드

vector<int> degeneracy_ordering(int n, const vector<vector<int>>& adj) {
	vector<int> deg(n + 1);
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
	for (int i = 1; i <= n; i++) {
		deg[i] = adj[i].size();
		pq.push({ deg[i], i });
	}
	vector<bool> removed(n + 1);
	vector<int> ret;
	while (pq.size()) {
		auto [val, i] = pq.top();
		pq.pop();
		if (removed[i]) continue;
		if (deg[i] != val) continue;
		removed[i] = 1;
		ret.push_back(i);
		for (int j : adj[i]) {
			if (removed[j]) continue;
			deg[j]--;
			pq.push({ deg[j], j });
		}
	}
	return ret;
}

degeneracy ordering은 std::priority_queue를 이용해 $\mathcal{O}((n + m)\log(n + m))$, std::set을 이용해 $\mathcal{O}((n + m)\log n)$에 구할 수 있고, 버킷 큐를 이용한 $\mathcal{O}(n + m)$ 알고리즘도 존재합니다.

이번 글에서는 편의를 위해 $\mathcal{O}((n + m)\log(n + m))$ 코드를 예시로 사용하겠습니다.

4. Subgraph Counting ($3$-nodes)

subgraph counting 문제에서 패턴 그래프 $H$의 정점 개수를 $k$라 할 때, $k = 3, 4$인 경우 여러 효율적인 알고리즘이 알려져 있습니다.

Fig.2

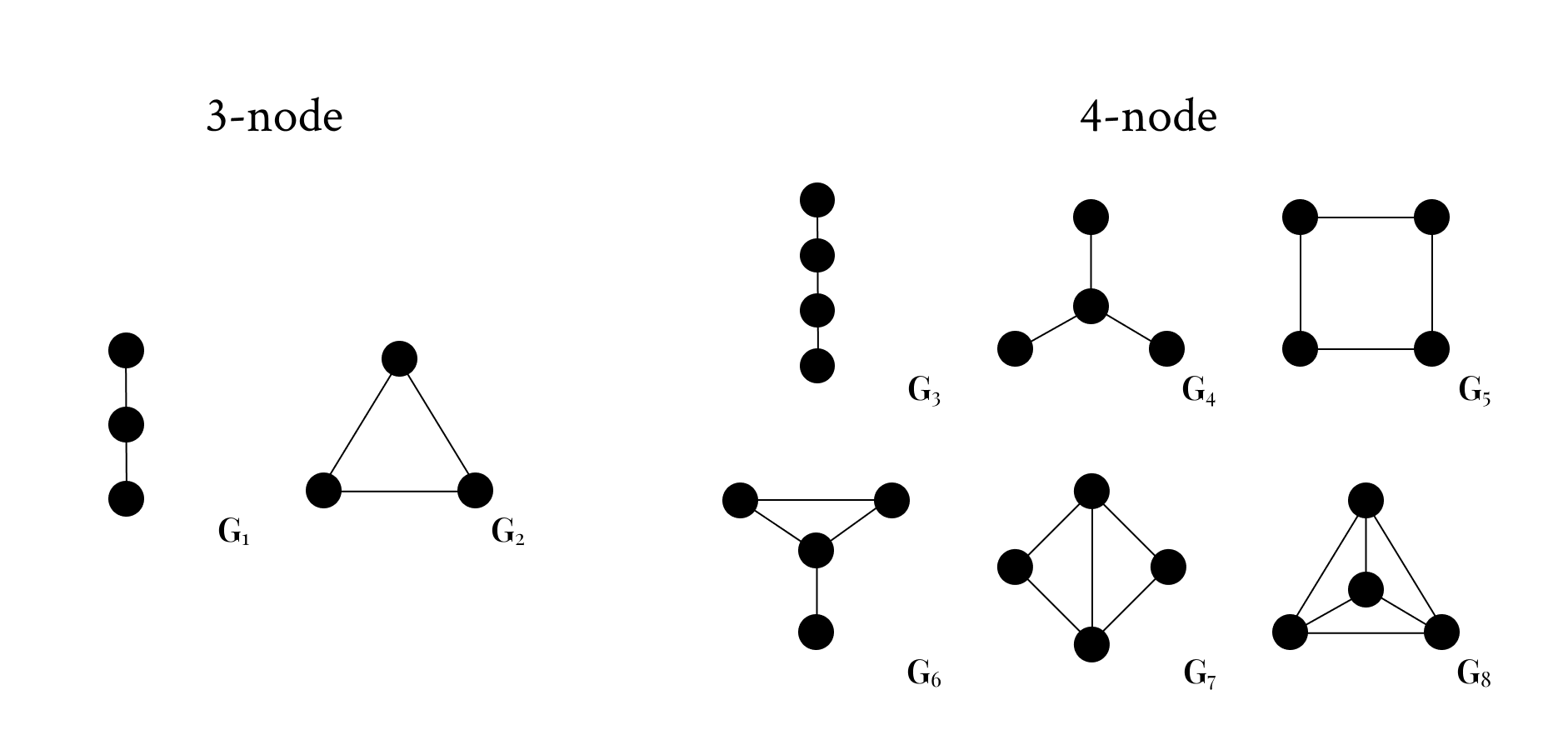
이번 단락에서는 $k = 3$인 두 가지 경우를 살펴보고, 다음 단락에서는 $k = 4$인 경우를 살펴보겠습니다.

표기의 편의를 위해 앞으로 별 다른 언급 없이 $n =

V(G)

, m =

E(G)

, k =

V(H)

, \operatorname{deg}(v) = \operatorname{deg}G(v)$를 사용하겠습니다. 또한, 그래프 $G$의 degeneracy ordering $L = [v_0, v_1, \cdots, v{n-1}]$에서 $i$번 정점이 등장하는 인덱스를 $\operatorname{rank}(i)$로 정의해 사용하겠습니다.

4.1 $P_3$ case

$H = P_3$인 경우는 중심 정점 $v$를 고정한 뒤 $\binom{\operatorname{deg}(v)}{2}$를 계산해 더해주면 $\mathcal{O}(n + m)$에 해결할 수 있습니다.

4.2 $C_3$ case

$H = C_3$인 경우는 그래프 $G$의 degeneracy ordering을 구한 뒤 $\operatorname{rank}(i) < \operatorname{rank}(j) < \operatorname{rank}(k)$인 $i \rightarrow j \rightarrow k$ 경로를 순회하면 해결할 수 있습니다.

구현 코드는 다음과 같습니다.

i64 count_3_cycle(int n, const vector<vector<int>>& adj) {
	vector<int> L = degeneracy_ordering(n, adj);
	vector<int> rank(n + 1);
	for (int i = 0; i < n; i++) rank[L[i]] = i;
	vector<vector<int>> g(n + 1);
	for (int i = 1; i <= n; i++) {
		for (int j : adj[i]) {
			if (rank[i] >= rank[j]) continue;
			g[i].push_back(j);
		}
	}
	i64 ret = 0;
	vector<int> c(n + 1);
	for (int i = 1; i <= n; i++) {
		for (int j : g[i]) c[j] = 1;
		for (int j : g[i]) for (int k : g[j]) if (c[k]) ret++;
		for (int j : g[i]) c[j] = 0;
	}
	return ret;
}

시간복잡도는 각 간선 $(i, j)$마다 $\mathcal{O}(d(G))$개의 $k$를 탐색하니 $\mathcal{O}(m \cdot d(G))$입니다.

이때 코드에서 $C_3$을 이루는 세 정점 $(i, j, k)$ tuple을 순회하며 직접 개수를 세니, $G$에서 $C_3$과 동형인 subgraph는 실제로 $\mathcal{O}(m \cdot d(G))$개입니다.

다음은 해당 방법으로 BOJ 1762번 문제를 해결하는 코드입니다. (코드)

4.3 $C_3$ case (alternative)

각 정점 $u$에 대해 degeneracy ordering에서 $u$보다 늦게 등장하는 $v$로 이어지는 $(u, v) \in E(G)$의 개수를 $\operatorname{outdeg}(u)$라 하면, $\operatorname{outdeg}(u) \le d(G)$가 성립합니다.

$V_i = { v \in V(G) \mid \operatorname{deg}(v) \ge i }$, $E_i = { (u, v) \in E(G) \mid u, v \in V_i }$를 정의합시다.

다음 사실이 성립합니다.

\[\begin{align*} \sum_{i=1}^{\infty}|V_i| &= \sum_{v\in V(G)}\operatorname{deg}(v) = 2m \\ |E_i| &\le \sum_{v \in V_i}\operatorname{outdeg}(v) \le d(G) \cdot |V_i| \\ \end{align*}\]

이때 $(u, v) \in E(G)$에 대한 $\min(\operatorname{deg}(u), \operatorname{deg}(v))$의 합은 $\sum_{i=1}^{\infty}

E_i

$와 같으니 $2m \cdot d(G)$ 이하입니다.

이 사실을 이용하면 degeneracy ordering을 명시적으로 구하지 않더라도 $(\operatorname{deg}(u), u)$가 감소하는 순서대로 $i \rightarrow j \rightarrow k$를 순회하면 같은 복잡도를 얻을 수 있습니다.

구현 코드는 다음과 같습니다.

i64 count_3_cycle(int n, const vector<vector<int>>& adj) {
	vector<vector<int>> g(n + 1);
	for (int i = 1; i <= n; i++) {
		for (int j : adj[i]) {
			if (adj[i].size() < adj[j].size()) continue;
			if (adj[i].size() == adj[j].size() && i <= j) continue;
			g[i].push_back(j);
		}
	}
	i64 ret = 0;
	vector<int> c(n + 1);
	for (int i = 1; i <= n; i++) {
		for (int j : g[i]) c[j] = 1;
		for (int j : g[i]) for (int k : g[j]) if (c[k]) ret++;
		for (int j : g[i]) c[j] = 0;
	}
	return ret;
}

해당 코드는 $(i, j)$ 간선마다 $\min(\operatorname{deg}(u), \operatorname{deg}(v))$만큼의 연산을 수행하니 $\mathcal{O}(\sum_{(u, v) \in E(G)}\min(\operatorname{deg}(u), \operatorname{deg}(v))) = \mathcal{O}(m \cdot d(G))$ 의 시간복잡도를 가집니다.

다음은 해당 방법으로 BOJ 1762번 문제를 해결하는 코드입니다. (코드)

5. Subgraph Counting ($4$-nodes)

Fig.2

$k = 4$인 경우는 $P_4, S_4, C_4$를 포함해 총 $6$가지 case가 있습니다.

5.1 $P_4$ case

$H = P_4$인 경우는 중심 간선 $(u, v)$를 고정한 뒤 $(\operatorname{deg}(u) - 1) \cdot (\operatorname{deg}(v) - 1)$를 계산해 더한 값을 $S$, $C_3$의 개수를 $T$라 할 때 $S - 3T$를 구하면 $C_3$와 마찬가지로 $\mathcal{O}(m \cdot d(G))$에 해결할 수 있습니다.

5.2 $S_4$ case

$H = S_4$인 경우는 중심 정점 $v$를 고정한 뒤 $\binom{\operatorname{deg}(v)}{3}$을 계산해 더해주면 $\mathcal{O}(n + m)$에 해결할 수 있습니다.

5.3 $C_4$ case

$H = C_4$인 경우는 $(\operatorname{deg}(u), u)$가 최대인 정점 $i$를 고정한 뒤, $(\operatorname{deg}(u), u)$가 $i$보다 작은 두 정점 $j, k$에 대해 $i \rightarrow j \rightarrow k$ 경로를 순회하면 해결할 수 있습니다.

구현 코드는 다음과 같습니다.

i64 count_4_cycle(int n, const vector<vector<int>>& adj) {
	i64 ret = 0;
	vector<int> c(n + 1);
	for (int i = 1; i <= n; i++) {
		vector<int> buc;
		for (int j : adj[i]) {
			if (adj[i].size() < adj[j].size()) continue;
			if (adj[i].size() == adj[j].size() && i <= j) continue;
			for (int k : adj[j]) {
				if (adj[i].size() < adj[k].size()) continue;
				if (adj[i].size() == adj[k].size() && i <= k) continue;
				if (c[k] == 0) buc.push_back(k);
				ret += c[k]++;
			}
		}
		for (int x : buc) c[x] = 0;
	}
	return ret;
}

시간복잡도는 $(u, v) \in E(G)$마다 $\min(\operatorname{deg}(u), \operatorname{deg}(v))$의 연산을 수행하니 $\mathcal{O}(m \cdot d(G))$입니다.

다음은 해당 방법으로 BOJ 32395번 문제를 해결하는 코드입니다. (코드)

5.4 Paw Graph

$C_3$에 간선 하나가 붙어있는 형태의 그래프를 paw graph라 부릅니다.

$H$가 paw graph일 때 subgraph counting 문제는 $C_3$을 순회하며 $\mathcal{O}(m \cdot d(G))$에 해결할 수 있습니다.

5.5 Diamond Graph

$K_4$에서 간선 하나를 제거한 그래프를 diamond graph라 부릅니다.

$H$가 diamond graph일 때 subgraph counting 문제는 $C_3$을 순회하며 각 $(u, v) \in E(G)$마다 $(u, v)$를 포함하는 $C_3$의 개수 $f(u, v)$를 구해둔 뒤 $\binom{f(u, v)}{2}$의 합을 구하면 $\mathcal{O}(m \cdot d(G))$에 해결할 수 있습니다.

5.6 $K_4$ case

$H = K_4$인 경우는 $(\operatorname{deg}(u), u)$가 최대인 대표 정점 $u$를 고정한 뒤, $(u, v, w)$가 $C_3$을 이루는 tuple을 순회하며 $(v, w) \in E(G)$를 모아 새로운 그래프 $G’$를 구성해 $C_3$ 개수의 합을 구하면 해결할 수 있습니다.

풀이의 시간복잡도는 $G’$에서 $C_3$의 개수를 구하는 시간복잡도가 $\mathcal{O}(

E(G’)

\cdot d(G’))$이고, $d(G’) \le d(G)$, $\sum

E(G’)

= \mathcal{O}(m \cdot d(G))$이니 $\mathcal{O}(m \cdot d(G)^2)$입니다. 이는 일반적인 상황에서 $d(G)$가 $\mathcal{O}(\sqrt m)$임을 생각해보면 너무 느립니다.

이때 $G’$에서 $C_3$의 개수를 구하는 부분을 bitset으로 대체하면 시간복잡도를 $\mathcal{O}(

V(G’)

E(G’)

/64)$로 만들 수 있고, 명시적으로 degeneracy ordering을 이용하면 $

V(G’)

\le d(G)$이니 $\mathcal{O}(m \cdot d(G) + m \cdot d(G)^2 / 64)$에 문제를 해결할 수 있습니다.

구현 코드는 다음과 같습니다.

i64 count_4_clique(int n, const vector<vector<int>>& adj) {
	vector<int> L = degeneracy_ordering(n, adj);
	vector<int> rank(n + 1);
	for (int i = 0; i < n; i++) rank[L[i]] = i;
	vector<vector<int>> g(n + 1);
	for (int i = 1; i <= n; i++) {
		for (int j : adj[i]) {
			if (rank[i] >= rank[j]) continue;
			g[i].push_back(j);
		}
	}
	i64 ret = 0;
	vector<int> c(n + 1, -1);
	for (int i = 1; i <= n; i++) {
		vector<vector<u64>> bs(g[i].size(), vector<u64>(g[i].size() + 63 >> 6));
		for (int j = 0; j < g[i].size(); j++) c[g[i][j]] = j;
		for (int j : g[i]) {
			for (int k : g[j]) {
				if (c[k] == -1) continue;
				int a = c[j];
				int b = c[k];
				bs[a][b >> 6] |= 1ULL << (b & 63);
				bs[b][a >> 6] |= 1ULL << (a & 63);
				for (int i = 0; i < bs[a].size(); i++) {
					ret += __builtin_popcountll(bs[a][i] & bs[b][i]);
				}
			}
		}
		for (int j : g[i]) c[j] = -1;
	}
	return ret;
}

다음은 해당 방법으로 BOJ 28200번 문제를 해결하는 코드입니다. (코드)

6. Subgraph Counting (more than $5$-nodes)

$k \ge 5$인 경우는 일반적으로 subquadratic 시간에 subgraph counting 문제를 해결하는 방법이 알려져 있지 않습니다. 이는 $k$가 커질 수록 패턴 그래프의 간선 수가 늘어나면서 탐색해야 하는 후보 집합이 기하급수적으로 커지기 때문입니다.

$k = 5$인 경우로 문제를 한정하면 몇몇 특수한 경우를 제외하면 대부분 $\mathcal{O}(m \cdot d(G)^3)$ 또는 그 이상의 연산량이 필요합니다. 이때 BOJ 14571과 같이 특정 패턴 그래프에 대해서는 $\mathcal{O}(m \cdot d(G))$ scale의 알고리즘이 존재하기도 합니다.

관련 연구 결과는 [3], [4], [6], [7]에서 확인해볼 수 있습니다.

7. Conclusion

이번 글에서는 그래프의 degeneracy를 이용한 subgraph counting 기법을 알아보았습니다.

degeneracy ordering를 이용하면 그래프의 $\operatorname{outdeg}$를 $d(G)$ 이하로 한정시켜 subgraph counting을 효율적으로 해결할 수 있습니다. degeneracy는 일반적인 경우 $\mathcal{O}(\sqrt m)$ scale으로 작고, 그래프의 구조가 특수한 경우는 $\mathcal{O}(1)$이 되기도 합니다. 또한 많은 경우 degeneracy는 $\sqrt m$ 이하로 작은 경우가 많으니, 위 기법은 실험적으로도 좋은 성능을 보입니다.

아래 표는 이 기법을 이용해 해결한 패턴별 알고리즘의 시간복잡도입니다.

패턴 그래프 $H$	$k$	시간복잡도	연습 문제
$P_3$	3	$\mathcal{O}(n + m)$	-
$C_3$	3	$\mathcal{O}(m \cdot d(G))$	BOJ 1762, Library Checker
$P_4$	4	$\mathcal{O}(m \cdot d(G))$	-
$S_4$	4	$\mathcal{O}(n + m)$	BOJ 31217
$C_4$	4	$\mathcal{O}(m \cdot d(G))$	BOJ 32395, Library Checker
paw graph	4	$\mathcal{O}(m \cdot d(G))$	-
diamond graph	4	$\mathcal{O}(m \cdot d(G))$	-
$K_4$	4	$\mathcal{O}(m \cdot d(G) + m \cdot d(G)^2 / 64)$	BOJ 28200

정점 수가 $k \ge 5$인 일반적인 경우에는 subquadratic 해법이 알려져 있지 않으나, 특정 그래프는 $k \le 4$의 기법을 응용해 효율적으로 해결할 수 있습니다.

subgraph counting 문제는 알고리즘 대회에 종종 등장하며, 그래프 이론에서 중요한 주제 중 하나입니다. 이번 글에서 다룬 내용은 subgraph counting을 해결하는 핵심적인 접근법이니, 익혀두면 다양한 그래프 문제를 풀 때 많은 도움이 될 거라 생각합니다.