Advanced Game Search Algorithms (1)

algorithm , game-theory , problem-solving

1. Introduction

이번 글에서는 게임 에이전트의 가장 단순한 형태인 Random Agent부터 시작하여 Greedy, Minimax, Alpha-Beta Pruning의 핵심 원리를 다룹니다. 이후 이어지는 글에서는 MCTS 등의 현대적인 탐색 기법을 알아보고, NNUE 등의 neural network를 이용한 평가 방법과 여러 search Pruning 방법을 살펴보겠습니다.

또한 에이전트의 성능을 객관적으로 평가하기 위해 SPRT(Sequential Probability Ratio Test)라는 평가 기법을 소개합니다. 이를 이용하면 통계적으로 두 에이전트 간의 실력 차이를 엄밀하게 검증할 수 있습니다.

이번 글에서 소개하는 방법론은 $2$인, 제로섬, 턴제, 완전정보, 결정론적 전이를 만족하는 게임에 적용이 가능하며, 구체적인 설명을 위해서 ATAXX를 예시로 각 알고리즘을 구현해보겠습니다.

2. ATAXX

게임 에이전트를 구현하는 방법을 알아보기에 앞서, 예시로 들 게임의 규칙을 먼저 소개하겠습니다.

2.1 게임 규칙

ATAXX는 $7 \times 7$ 보드에서 진행되는 $2$인 턴제 게임입니다.

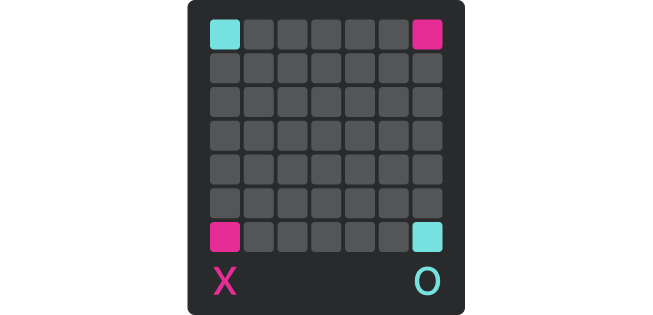
선공 플레이어는 $(1, 1), (7, 7)$ 위치에 두 개의 돌을 가지고 있고, 후공 플레이어는 $(1, 7)$, $(7, 1)$ 위치에 두 개의 돌을 가지고 있습니다. 나머지 $45$개의 칸은 모두 빈 칸입니다.

게임은 두 플레이어가 번갈아가며 본인의 돌이 놓여있는 시작 칸 $(x_1, y_1)$과 비어있는 도착 칸 $(x_2, y_2)$를 고르며 진행됩니다.

각 턴마다 게임이 진행되는 방식은 다음과 같습니다.

이동 거리 $d = \max(\lvert x_2 - x_1\rvert, \lvert y_2 - y_1\rvert)$는 $1$ 또는 $2$여야 합니다.
이동 거리가 $1$인 경우는 시작 칸의 돌이 그대로 남고 도착 칸에만 자신의 돌이 새로 생깁니다.
이동 거리가 $2$인 경우는 시작 칸의 돌이 도착 칸으로 이동합니다.
도착 칸 $(x_2, y_2)$를 기준으로 $8$방향(상하좌우, 대각선)으로 인접한 칸에 상대의 돌이 있다면, 해당 칸을 자신의 돌로 바꿉니다.
자신의 턴에 고를 수 있는 $(x_1, y_1), (x_2, y_2)$가 없다면 PASS를 선택하며, 이 경우에는 아무 변화 없이 상대에게로 턴이 넘어갑니다.

정리하면, 각 플레이어는 이동거리가 $1$ 또는 $2$인 $(x_1, y_1), (x_2, y_2)$를 골라 턴을 진행하며, 고를 수 있는 행동이 없다면 PASS를 선택해 턴을 넘깁니다.

다음은 선공 플레이어가 $(1, 1)$에서 $(2, 2)$로 이동 거리가 $1$인 행동을 수행하는 예시입니다.

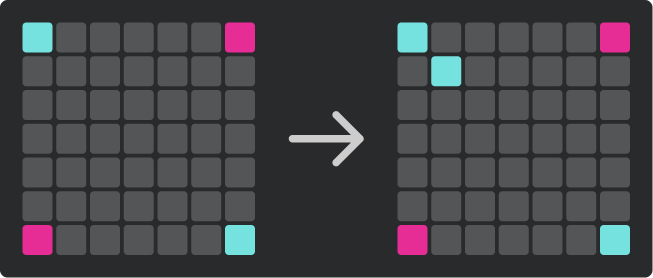
다음은 후공 플레이어가 $(2, 2)$에서 $(4, 4)$로 이동 거리가 $2$인 행동을 수행하는 예시입니다.

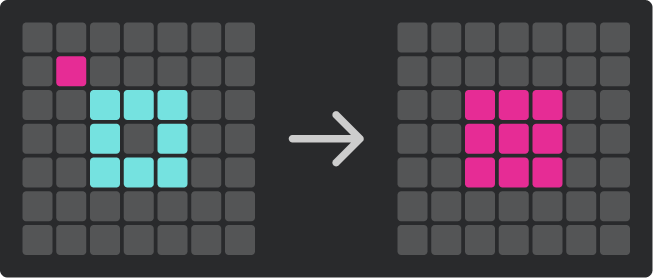
마지막으로 다음은 선공 플레이어가 PASS를 선택하는 예시입니다.

게임은 다음 조건 중 하나가 만족되면 종료됩니다.

어느 한 플레이어의 돌이 보드에서 완전히 사라졌을 때
보드에 남은 빈 칸이 하나도 없을 때
두 플레이어가 모두 $200$번씩 총 $400$턴을 수행했을 때

종료 시점에 돌이 더 많은 플레이어가 승리하며, 만약 두 플레이어의 돌 개수가 같다면 무승부로 마무리합니다.

여기까지가 ATAXX 게임의 룰입니다. $400$턴을 초과하면 게임을 종료한다는 규칙은 게임이 무한히 길어지는 걸 방지하기 위해 임의로 추가했습니다. 다른 플랫폼에서는 $3$회 동형, $50$수 규칙 등을 채택할 수 있음에 주의해주세요.

note. 해당 게임은 여기에서 플레이해볼 수 있습니다.

2.2 입출력 형식

이제 에이전트와 심판 프로그램 간의 상호작용 규칙을 정의하겠습니다.

명령어	심판→에이전트(입력)	에이전트→심판 (출력)	시간 제한(ms)	설명
READY	`READY (FIRST \\| SECOND)`	`OK`	`3000`	선공/후공 정보를 알립니다.
TURN	`TURN my_time opp_time`	`MOVE x1 y1 x2 y2`	`my_time`	내 남은 시간과 상대의 남은 시간을 알립니다. 이번 턴에 내가 선택한 수의 $(x_1, y_1)$, $(x_2, y_2)$를 출력합니다. `PASS`를 선택한 경우는 `MOVE -1 -1 -1 -1`을 출력합니다.
OPP	`OPP x1 y1 x2 y2 time`	-	-	상대가 직전에 둔 수와 사용한 시간을 알립니다. 상대가 `PASS`를 선택한 경우는 `OPP -1 -1 -1 -1 time`이 입력됩니다.
FINISH	`FINISH`	-	-	게임 종료를 알립니다. 에이전트는 추가 출력 없이 프로그램을 정상 종료해야 합니다.

각 에이전트의 제한 시간은 게임 당 10000ms로 주어지고, 에이전트는 주어진 시간을 잘 분배해서 사용해야 합니다.

이제 이 형식에 맞춰서 게임 에이전트를 구현해보며 여러 방법론의 장단점을 알아보겠습니다.

3. Random Agent

가장 먼저 생각해볼 수 있는 정책은 가능한 행동 중 아무 행동이나 랜덤하게 고르는 것입니다.

랜덤 정책을 위의 입출력 형식에 맞게 구현한 코드는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

struct board {
	board() : v{} {
		v[1][1] = v[7][7] = 1;
		v[1][7] = v[7][1] = 2;
	}
	void apply_move(int x1, int y1, int x2, int y2, int turn) {
		if (x1 == -1 && y1 == -1 && x2 == -1 && y2 == -1) return;
		int d = max(abs(x2 - x1), abs(y2 - y1));
		if (d == 2) v[x1][y1] = 0;
		v[x2][y2] = turn;
		for (int x = x2 - 1; x <= x2 + 1; x++) {
			for (int y = y2 - 1; y <= y2 + 1; y++) {
				if (x < 1 || x > 7 || y < 1 || y > 7) continue;
				if (v[x][y] == (turn ^ 3)) v[x][y] = turn;
			}
		}
	}
	int get(int x, int y) const {
		return v[x][y];
	}
private:
	int v[8][8];
};

int gen_rand(int l, int r) {
	static mt19937 rd(42);
	return uniform_int_distribution(l, r)(rd);
}

auto find_move(board game, int turn) {
	tuple ret(-1, -1, -1, -1);
	int cnt = 0;
	for (int x1 = 1; x1 <= 7; x1++) {
		for (int y1 = 1; y1 <= 7; y1++) {
			if (game.get(x1, y1) != turn) continue;
			for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
				if (x2 < 1 || x2 > 7) continue;
				for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
					if (y2 < 1 || y2 > 7) continue;
					if (x2 == x1 && y2 == y1) continue;
					if (game.get(x2, y2) != 0) continue;
					if (gen_rand(1, ++cnt) == 1) ret = tuple(x1, y1, x2, y2);
				}
			}
		}
	}
	return ret;
}

int main() {
	board game;
	int turn;
	while (1) {
		string s; getline(cin, s);
		istringstream in(s);
		string cmd; in >> cmd;
		if (cmd == "READY") {
			string t; in >> t;
			turn = t == "FIRST" ? 1 : 2;
			cout << "OK" << endl;
		}
		else if (cmd == "TURN") {
			int t1, t2; in >> t1 >> t2;
			auto [x1, y1, x2, y2] = find_move(game, turn);
			game.apply_move(x1, y1, x2, y2, turn);
			cout << "MOVE " << x1 << ' ' << y1 << ' ' << x2 << ' ' << y2 << endl;
		}
		else if (cmd == "OPP") {
			int x1, y1, x2, y2; in >> x1 >> y1 >> x2 >> y2;
			int t2; in >> t2;
			game.apply_move(x1, y1, x2, y2, turn ^ 3);
		}
		else if (cmd == "FINISH") {
			break;
		}
		else {
			assert(0);
		}
	}
}

코드에서 find_move 함수는 $(x_1, y_1, x_2, y_2)$ 조합을 모두 확인하며 가능한 행동을 균등한 확률로 선택합니다. 만약 가능한 조합이 없다면 PASS를 의미하는 $(-1, -1, -1, -1)$을 반환합니다.

apply_move 함수는 turn에 해당하는 플레이어가 $(x_1, y_1, x_2, y_2)$를 선택했을 때 보드의 변화를 반영하는 역할을 수행합니다.

랜덤 정책은 이후 구현할 정책들의 성능을 비교하기 위한 기준선(Baseline)입니다. 새로운 정책이 효과적이라면 랜덤 정책보다 높은 승률을 보여야 하며, 이를 통해 최소한의 성능을 검증하고 구현상의 오류를 조기에 발견할 수 있습니다.

4. Greedy Agent

다음으로 find_move 함수에서 평가 함수를 이용해 $(x_1, y_1, x_2, y_2)$ 중 평가값이 최대인 행동을 그리디하게 고르는 정책을 알아보겠습니다.

int eval(board game, int turn) {
	int ret = 0;
	for (int x = 1; x <= 7; x++) {
		for (int y = 1; y <= 7; y++) {
			int val = game.get(x, y);
			if (val == turn) ret++;
			if (val == (turn ^ 3)) ret--;
		}
	}
	return ret;
}

auto find_move(board game, int turn) {
	tuple opt_move(-1, -1, -1, -1);
	int opt_val = -(1 << 30);
	for (int x1 = 1; x1 <= 7; x1++) {
		for (int y1 = 1; y1 <= 7; y1++) {
			if (game.get(x1, y1) != turn) continue;
			for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
				if (x2 < 1 || x2 > 7) continue;
				for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
					if (y2 < 1 || y2 > 7) continue;
					if (x2 == x1 && y2 == y1) continue;
					if (game.get(x2, y2) != 0) continue;
					board nxt = game;
					nxt.apply_move(x1, y1, x2, y2, turn);
					int val = eval(nxt, turn);
					if (opt_val < val) {
						opt_move = tuple(x1, y1, x2, y2);
						opt_val = val;
					}
				}
			}
		}
	}
	return opt_move;
}

코드는 랜덤 정책에서 eval 함수를 새로 구현한 뒤 find_move 함수를 이에 맞춰 수정해주면 구현할 수 있습니다.

eval 함수는 game과 turn 인자를 받아 현재 보드의 상태가 game일 때 turn에 해당하는 플레이어가 유리한 정도를 나타내는 값을 반환합니다.

이를 구현하는 방법은 여러가지가 있습니다. 먼저 떠올릴 수 있는 방법은 두 플레이어가 최적으로 플레이할 때 결과가 승리라면 $1$, 무승부라면 $0.5$, 패배라면 $0$을 반환하도록 하는 것입니다. 이 정의에 맞는 eval 함수를 구현할 수 있다면 그리디 정책은 실제로 최적의 수를 구합니다. 하지만 게임의 특성 상 game tree가 너무 커서 이 값을 실제로 구하기는 실질적으로 어렵습니다.

이에 대한 대안으로는 turn에 해당하는 돌의 개수에서 turn ^ 3에 해당하는 돌의 개수를 뺀 값을 반환하도록 하는 휴리스틱 함수를 생각해볼 수 있습니다. 이는 돌 개수가 더 많다면 이길 가능성이 높다는 가정을 바탕으로 유리한 정도를 표현한 함수로, 실제로는 다음 턴에 상대가 어떤 행동을 고르는지에 따라 승패가 뒤집힐 수 있기에 정확한 모델링이 아니지만 근사적으로 eval 함수를 구성할 수 있다는 장점이 있습니다. 여기서는 이 방법을 사용하며, eval 함수를 개선하는 방법은 다음 글에서 다루겠습니다.

find_move 함수는 eval 함수를 이용해 행동을 수행한 뒤의 보드의 평가값을 구하고, 이 값이 최대가 되는 행동을 반환합니다. 만약 평가값이 최대인 행동이 여러 개라면 $(x_1, y_1, x_2, y_2)$가 사전순으로 최소인 행동을 반환하도록 했습니다.

그리디 정책은 eval 함수가 게임의 유불리를 얼마나 정확히 모델링하는가에 따라 성능이 달라집니다. 하지만 돌 개수의 차이와 같은 간단한 모델링만 이용하더라도 랜덤 정책보다는 성능이 개선됨을 기대할 수 있습니다.

5. SPRT(Sequential Probability Ratio Test)

지금까지 랜덤 정책과 그리디 정책을 알아보았습니다. 이번 단락에서는 두 정책의 성능을 비교하는 통계적 기법인 SPRT(Sequential Probability Ratio Test)를 알아보겠습니다.

두 정책의 성능을 비교하는 가장 간단한 방법은 여러 번 두 정책끼리 대결을 시켜보는 것입니다. 예를 들어 $100$번 매칭을 돌렸는데 첫 번째 정책이 $20$번, 두 번째 정책이 $80$번 승리했다면 두 번째 정책이 첫 번째 정책보다 더 우수하다고 판단할 수 있습니다. 하지만 이 방법은 두 정책의 실제 승률을 근사적으로 정확하게 구하기 위해선 많은 시행 횟수가 필요하고, 종료 시점 또한 명확히 정하기 어렵다는 단점이 있습니다.

이를 보완하기 위해 일반적으로 사용하는 방법이 SPRT 기법입니다. SPRT 기법을 알아보기에 앞서 먼저 Elo Rating 체계를 알아보겠습니다.

Elo Rating 체계는 다음과 같은 수식으로 두 에이전트 $A, B$의 실력을 두 실수 $R_A, R_B$로 모델링합니다.

\[\begin{align*} E_A &= \frac{1}{1 + 10^{(R_B - R_A) / 400}} \\ E_B &= \frac{1}{1 + 10^{(R_A - R_B) / 400}} \end{align*}\]

$E_A, E_B$는 $A, B$의 예상 승률을 나타내며, $E_A = \frac{1}{1 + u}, E_B = \frac{1}{1 + u^{-1}} = \frac{u}{1 + u}$에서 $E_A + E_B = 1$이 성립합니다.

예를 들어서 $R_A = 1900, R_B = 1500$는 $E_A = 0.9091, E_B = 0.0909$에서 $A$가 $90.91$%의 승률을 보일 것을 의미합니다. 여기서 $R_A, R_B$를 Elo Rating이라 부르며, Elo Rating의 단위는 elo입니다.

이제 SPRT 기법을 이용해 에이전트 $A$보다 $B$가 좋은지 여부를 판별하는 방법을 알아보겠습니다. SPRT 기법은 에이전트 $A, B$의 Elo Rating의 차이가 $0$ 또는 $50$ 두 가지 값 중 하나라는 걸 가정하며, 이 가정 하에서 둘 중 어느 가설이 더 확률적으로 타당한지 검증합니다.

다음의 두 가지 가설을 세워보겠습니다.

$H_0$: 에이전트 $A$는 에이전트 $B$보다 Elo Rating이 $0$ elo 더 높다.
$H_1$: 에이전트 $A$는 에이전트 $B$보다 Elo Rating이 $50$ elo 더 높다.

두 가설에서 에이전트 $A$가 이기거나 질 확률은 다음과 같습니다.

\[\begin{align*} p(W | H_0) &= 0.5 \\ p(L | H_0) &= 0.5 \\ p(W | H_1) &= 0.5715 \\ p(L | H_1) &= 0.4285 \\ \end{align*}\]

두 에이전트를 $n$판 대결시킨 결과를 $x_1, \cdots, x_n$이라 하겠습니다. $i$번째 판에서 에이전트 $A$가 승리했다면 $x_i = 1$, 패배했다면 $x_i = 0$입니다. 편의를 위해 무승부인 경우는 없다고 가정하겠습니다.

$i$번째 판의 로그 우도비(log-likelihood ratio)은 다음과 같이 계산됩니다.

\[l_i = \log \frac{p(x_i | H_1)}{p(x_i | H_0)} = x_i \log \frac{p(W | H_1)}{p(W | H_0)} + (1 - x_i)\log \frac{p(L | H_1)}{p(L | H_0)}\]

이를 누적한 값은 다음과 같습니다.

\[S_n = \displaystyle\sum_{i=1}^n l_i = W_n \log \frac{p(W | H_1)}{p(W | H_0)} + (n - W_n) \log \frac{p(L | H_1)}{p(L | H_0)}\]

여기서 $W_n = \sum x_i$는 $n$판 중 에이전트 $A$가 승리한 횟수입니다.

이제 $S_n$을 이용하면 두 가설 중 어느 가설이 옳은지를 검증할 수 있습니다. $H_0$이 참인데 $H_1$를 잘못 채택하는 확률을 $\alpha$, $H_1$이 참인데 $H_0$을 잘못 채택하는 확률을 $\beta$로 설정합시다. 다음 사실이 알려져있습니다.

$S_n \ge log(\frac{1 - \beta}{\alpha})$라면 $H_1$을 선택한다.
$S_n \le log(\frac{\beta}{1 - \alpha})$라면 $H_0$을 선택한다.
둘 다 아니라면 대결을 더 진행하며 위의 과정을 반복한다.
이 방식을 이용하면 $\alpha, \beta$의 정의에 맞게 가설을 검정할 수 있다.

일반적으로 SPRT를 이용할 때는 $\alpha = \beta = 0.05$를 사용합니다.

note. 수식의 수학적 유도는 이 글과 이 글을 참고해주세요.

Agent 1 (H1): test/greedy
Agent 2 (H0): test/random
Elo [H0, H1]: [0.0, 50.0] -> P [P0, P1]: [0.5000, 0.5715]
LLR bounds: [-2.944, 2.944] (Alpha=0.05, Beta=0.05)
LLR updates: Win=+0.1336, Loss=-0.1542, Draw=0.0

[SPRT Finished]
Total: 23, WLD: 23/0/0, LLR: 3.073 [-2.944, 2.944]
Final LLR: 3.073
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

이를 이용해 랜덤 정책과 그리디 정책을 비교해보면 그리디 정책이 랜덤 정책보다 우수함을 보일 수 있습니다.

6. Minimax Algorithm

그리디 정책은 $1$턴 이후의 eval 값이 최대가 되는 행동을 고르는 전략을 사용합니다. 이때 $1$턴이 아니라 그 이상을 볼 수 있다면 성능을 개선할 수 있을 것입니다.

6.1 Minimax Algorithm

Minimax Algorithm은 두 플레이어가 최선의 행동만을 한다고 가정할 때 각 state에서 어느 값을 선택할 것인지를 구하는 알고리즘입니다. 이때 최선의 행동이란 게임이 끝난 시점에 자신의 eval값을 최대화하는 행동을 의미합니다. 즉, 첫 번째 플레이어는 첫 번째 플레이어를 기준으로 구한 eval 값을 최대화하려고 하고, 두 번째 플레이어는 두 번째 플레이어를 기준으로 구한 eval 값을 최대화하려고 합니다.

이때 eval 함수의 정의가 대칭적이라면 두 플레이어를 각각 기준삼아 구한 eval 값의 합이 $0$일 것입니다. 이 경우에는 첫 번째 플레이어를 기준으로 구한 eval 값에 대해 첫 번째 플레이어는 이 값을 최대화하려고 할 것이고, 두 번째 플레이어는 이 값을 최소화하려고 할 것입니다.

이 전략을 game tree에서 생각해보면 노드의 depth의 parity에 따라 자식 node의 반환값 중 최소, 최대인 값을 현재 노드의 반환값으로 삼으며 각 노드에서 최적의 행동을 할 때 반환값을 구할 수 있습니다. 이때 리프 노드의 반환값은 해당 노드의 eval 값입니다. 이를 Minimax Algorithm이라 합니다.

이때 game tree를 모두 탐색하는 건 game tree가 지수적으로 커질 수 있기 때문에 현실적으로 어렵습니다. 따라서 대부분의 경우 Minimax Algorithm은 탐색 깊이를 제한한 뒤 최대 깊이에 도달하면 해당 노드의 eval 값을 반환하도록 하는 커팅을 수행합니다. 이는 해당 노드에서 플레이를 마저 이어나갈 때 얻어지는 최적의 eval 값를 직접 구하기가 어려우니 대안적으로 해당 노드의 평가값을 구하는 방식이기에 정확도가 떨어질 수 있습니다.

다음은 탐색 깊이를 $3$으로 제한한 Minimax Algorithm의 구현입니다.

constexpr int max_depth = 3;

int dfs(board game, int turn, int dep, auto& opt_move) {
	int mask = 0;
	for (int x = 1; x <= 7; x++) {
		for (int y = 1; y <= 7; y++) {
			mask |= 1 << game.get(x, y);
		}
	}
	if (dep == max_depth || mask != 7) return eval(game, turn);
	if (dep % 2 == 0) {
		int ret = -(1 << 30);
		int flag = 0;
		for (int x1 = 1; x1 <= 7; x1++) {
			for (int y1 = 1; y1 <= 7; y1++) {
				if (game.get(x1, y1) != turn) continue;
				for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
					if (x2 < 1 || x2 > 7) continue;
					for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
						if (y2 < 1 || y2 > 7) continue;
						if (x2 == x1 && y2 == y1) continue;
						if (game.get(x2, y2) != 0) continue;
						board nxt = game;
						nxt.apply_move(x1, y1, x2, y2, turn);
						flag = 1;
						int res = dfs(nxt, turn, dep + 1, opt_move);
						if (ret < res) {
							ret = res;
							if (dep == 0) opt_move = tuple(x1, y1, x2, y2);
						}
					}
				}
			}
		}
		if (flag == 0) {
			int res = dfs(game, turn, dep + 1, opt_move);
			if (ret < res) {
				ret = res;
				if (dep == 0) opt_move = tuple(-1, -1, -1, -1);
			}
		}
		return ret;
	}
	else {
		int ret = 1 << 30;
		int flag = 0;
		for (int x1 = 1; x1 <= 7; x1++) {
			for (int y1 = 1; y1 <= 7; y1++) {
				if (game.get(x1, y1) != (turn ^ 3)) continue;
				for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
					if (x2 < 1 || x2 > 7) continue;
					for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
						if (y2 < 1 || y2 > 7) continue;
						if (x2 == x1 && y2 == y1) continue;
						if (game.get(x2, y2) != 0) continue;
						board nxt = game;
						nxt.apply_move(x1, y1, x2, y2, turn ^ 3);
						flag = 1;
						int res = dfs(nxt, turn, dep + 1, opt_move);
						if (ret > res) {
							ret = res;
						}
					}
				}
			}
		}
		if (flag == 0) {
			int res = dfs(game, turn, dep + 1, opt_move);
			if (ret > res) {
				ret = res;
			}
		}
		return ret;
	}
}

auto find_move(board game, int turn) {
	tuple opt_move(-1, -1, -1, -1);
	dfs(game, turn, 0, opt_move);
	return opt_move;
}

코드에서 dfs 함수는 현재 탐색 깊이 dep를 인자로 가지고 있어 탐색이 최대 깊이에 도달하거나 게임이 종료되었다면 해당 상태의 eval 값을 반환합니다. 그렇지 않다면 dep의 parity에 따라 다음 상태의 반환값의 최대, 최솟값을 구하며 두 플레이어의 최적 행동을 구합니다.

현재 상태에서 가능한 행동이 존재하지 않는다면 flag를 이용하여 PASS를 수행해야 합니다.

6.2 Negamax Algorithm

이때 $\min(a, b) = -\max(-b, -a)$임을 이용하면 dep의 parity에 따른 조건분기 없이 하나의 로직으로 Minimax Algorithm을 구현할 수 있습니다. 이를 Negamax Algorithm이라 합니다.

각 state에서 두 플레이어가 모두 자신을 기준으로 하는 eval 함수를 최대화하려 할 때, 최댓값을 반환한다고 합시다. 이 정의를 이용하면 다음 상태의 반환값에 $-1$을 곱한 값의 최댓값을 구하며 dep의 parity와 관계없이 일관된 로직으로 Minimax Algorithm을 구현할 수 있습니다.

구현 코드는 다음과 같습니다.

int dfs(board game, int turn, int dep, auto& opt_move) {
	int mask = 0;
	for (int x = 1; x <= 7; x++) {
		for (int y = 1; y <= 7; y++) {
			mask |= 1 << game.get(x, y);
		}
	}
	if (dep == max_depth || mask != 7) {
		return eval(game, turn);
	}
	int ret = -(1 << 30);
	int flag = 0;
	for (int x1 = 1; x1 <= 7; x1++) {
		for (int y1 = 1; y1 <= 7; y1++) {
			if (game.get(x1, y1) != turn) continue;
			for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
				if (x2 < 1 || x2 > 7) continue;
				for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
					if (y2 < 1 || y2 > 7) continue;
					if (x2 == x1 && y2 == y1) continue;
					if (game.get(x2, y2) != 0) continue;
					board nxt = game;
					nxt.apply_move(x1, y1, x2, y2, turn);
					flag = 1;
					int res = -dfs(nxt, turn ^ 3, dep + 1, opt_move);
					if (ret < res) {
						ret = res;
						if (dep == 0) opt_move = tuple(x1, y1, x2, y2);
					}
				}
			}
		}
	}
	if (flag == 0) {
		int res = -dfs(game, turn ^ 3, dep + 1, opt_move);
		if (ret < res) {
			ret = res;
			if (dep == 0) opt_move = tuple(-1, -1, -1, -1);
		}
	}
	return ret;
}

Negamax Algorithm을 이용한 코드는 Minimax Algorithm과 항상 동일한 결과를 반환합니다.

Agent 1 (H1): test/minimax
Agent 2 (H0): test/greedy
Elo [H0, H1]: [0.0, 50.0] -> P [P0, P1]: [0.5000, 0.5715]
LLR bounds: [-2.944, 2.944] (Alpha=0.05, Beta=0.05)
LLR updates: Win=+0.1336, Loss=-0.1542, Draw=0.0

[SPRT Finished]
Total: 23, WLD: 23/0/0, LLR: 3.073 [-2.944, 2.944]
Final LLR: 3.073
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

마찬가지로 랜덤, 그리디 정책과 Minimax Algorithm을 이용한 정책을 SPRT를 이용해 비교해보면 개선이 되었음을 알 수 있습니다.

Agent 1 (H1): test/minimax
Agent 2 (H0): test/negamax
Elo [H0, H1]: [0.0, 50.0] -> P [P0, P1]: [0.5000, 0.5715]
LLR bounds: [-2.944, 2.944] (Alpha=0.05, Beta=0.05)
LLR updates: Win=+0.1336, Loss=-0.1542, Draw=0.0

[SPRT Finished]
Total: 286, WLD: 143/143/0, LLR: -2.951 [-2.944, 2.944]
Final LLR: -2.951
Result: Accept H0. Agent 1 is likely not better (Elo <= 0.0).

Minimax Algorithm과 Negamax Algorithm을 비교한 결과는 위와 같습니다. 두 코드는 정확히 같은 결과를 반환하며 SPRT에서 결과를 구할 때 선후공을 번갈아 진행하도록 하였기에 두 코드는 모두 $143$승 $143$패 $0$무로 같은 전적을 가집니다.

7. Alpha-Beta Pruning

마지막으로 Alpha-Beta Pruning 기법을 알아보겠습니다.

7.1 Alpha-Beta Pruning

6.1절의 Minimax Algorithm은 max_depth까지 모든 가능한 자식 노드를 탐색하기 때문에, 탐색해야 할 노드의 수가 깊이에 따라 지수적으로 증가한다는 단점이 있습니다.

Alpha-Beta Pruning(알파-베타 가지치기)은 Minimax Algorithm의 결과를 그대로 유지하면서, 탐색 트리의 최종 값에 영향을 주지 않는 것이 확실한 분기를 탐색하지 않고 잘라내는 최적화 기법입니다.

이 알고리즘은 $\alpha$와 $\beta$ 두 개의 변수를 이용해 탐색 범위를 관리합니다. $\alpha$는 현재 플레이어가 현재까지 탐색한 노드에서 찾은 최대 eval 값입니다. $\beta$는 상대 플레이어가 현재까지 탐색한 노드에서 찾은 최소 eval 값입니다.

$\alpha$와 $\beta$를 이용한 가지치기는 현재 플레이어의 차례에서 자식 노드의 반환값 res가 $\beta$ 이상인 경우와 상대 플레이어의 차례에서 자식 노드의 반환값 res가 $\alpha$ 이하인 경우 발생합니다. 전자는 부모 상태에서 상대 플레이어가 현재 상태를 절대 고르지 않을 것이기 때문에 최적의 플레이에서 나올 수 없는 상태이고, 후자도 마찬가지로 부모 상태에서 현재 플레이어가 절대 고르지 않을 상태이니 나올 수가 없어서 가지치기를 해도 결과가 변하지 않습니다.

이를 정리하면, 탐색 도중 $\alpha \ge \beta$가 되는 순간 가지치기를 하며 Minimax Algorithm을 개선할 수 있습니다. 이때 Alpha-Beta Pruning을 적용한 Minimax Algorithm은 기존과 항상 같은 결과를 반환합니다.

구현 코드는 다음과 같습니다.

constexpr int max_depth = 3;

int dfs(board game, int turn, int dep, int alpha, int beta, auto& opt_move) {
	int mask = 0;
	for (int x = 1; x <= 7; x++) {
		for (int y = 1; y <= 7; y++) {
			mask |= 1 << game.get(x, y);
		}
	}
	if (dep == max_depth || mask != 7) {
		return eval(game, turn);
	}
	if (dep % 2 == 0) {
		int ret = -(1 << 30);
		int flag = 0;
		for (int x1 = 1; x1 <= 7; x1++) {
			for (int y1 = 1; y1 <= 7; y1++) {
				if (game.get(x1, y1) != turn) continue;
				for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
					if (x2 < 1 || x2 > 7) continue;
					for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
						if (y2 < 1 || y2 > 7) continue;
						if (x2 == x1 && y2 == y1) continue;
						if (game.get(x2, y2) != 0) continue;
						board nxt = game;
						nxt.apply_move(x1, y1, x2, y2, turn);
						flag = 1;
						int res = dfs(nxt, turn, dep + 1, alpha, beta, opt_move);
						if (alpha < res) alpha = res;
						if (alpha >= beta) return alpha;
						if (ret < res) {
							ret = res;
							if (dep == 0) opt_move = tuple(x1, y1, x2, y2);
						}
					}
				}
			}
		}
		if (flag == 0) {
			int res = dfs(game, turn, dep + 1, alpha, beta, opt_move);
			if (ret < res) {
				ret = res;
				if (dep == 0) opt_move = tuple(-1, -1, -1, -1);
			}
		}
		return ret;
	}
	else {
		int ret = 1 << 30;
		int flag = 0;
		for (int x1 = 1; x1 <= 7; x1++) {
			for (int y1 = 1; y1 <= 7; y1++) {
				if (game.get(x1, y1) != (turn ^ 3)) continue;
				for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
					if (x2 < 1 || x2 > 7) continue;
					for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
						if (y2 < 1 || y2 > 7) continue;
						if (x2 == x1 && y2 == y1) continue;
						if (game.get(x2, y2) != 0) continue;
						board nxt = game;
						nxt.apply_move(x1, y1, x2, y2, turn ^ 3);
						flag = 1;
						int res = dfs(nxt, turn, dep + 1, alpha, beta, opt_move);
						if (beta > res) beta = res;
						if (alpha >= beta) return beta;
						if (ret > res) {
							ret = res;
						}
					}
				}
			}
		}
		if (flag == 0) {
			int res = dfs(game, turn, dep + 1, alpha, beta, opt_move);
			if (ret > res) {
				ret = res;
			}
		}
		return ret;
	}
}

auto find_move(board game, int turn) {
	tuple opt_move(-1, -1, -1, -1);
	dfs(game, turn, 0, -(1 << 30), 1 << 30, opt_move);
	return opt_move;
}

find_move 함수는 dfs를 호출할 때 $\alpha$를 음의 무한대를 의미하는 -(1 << 30), $\beta$를 양의 무한대를 의미하는 1 << 30으로 설정하여 탐색을 시작합니다.

7.2 Negamax-Style Alpha-Beta Pruning

6.2절에서 Minimax Algorithm을 Negamax Algorithm으로 변환하여 코드를 간소화했듯이, 7.1절의 Alpha-Beta Pruning 또한 Negamax 스타일로 구현할 수 있습니다.

아이디어는 6.2절과 동일하게 모든 노드에서 eval 값을 최대화하려고 시도하되, 자식 노드의 반환값에 $-1$을 곱하여 부호를 뒤집은 뒤 최댓값을 구하는 것입니다.

구현 코드는 다음과 같습니다.

int dfs(board game, int turn, int dep, int alpha, int beta, auto& opt_move) {
	int mask = 0;
	for (int x = 1; x <= 7; x++) {
		for (int y = 1; y <= 7; y++) {
			mask |= 1 << game.get(x, y);
		}
	}
	if (dep == max_depth || mask != 7) {
		return eval(game, turn);
	}
	int ret = -(1 << 30);
	int flag = 0;
	for (int x1 = 1; x1 <= 7; x1++) {
		for (int y1 = 1; y1 <= 7; y1++) {
			if (game.get(x1, y1) != turn) continue;
			for (int x2 = x1 - 2; x2 <= x1 + 2; x2++) {
				if (x2 < 1 || x2 > 7) continue;
				for (int y2 = y1 - 2; y2 <= y1 + 2; y2++) {
					if (y2 < 1 || y2 > 7) continue;
					if (x2 == x1 && y2 == y1) continue;
					if (game.get(x2, y2) != 0) continue;
					board nxt = game;
					nxt.apply_move(x1, y1, x2, y2, turn);
					flag = 1;
					int res = -dfs(nxt, turn ^ 3, dep + 1, -beta, -alpha, opt_move);
					if (alpha < res) alpha = res;
					if (alpha >= beta) return alpha;
					if (ret < res) {
						ret = res;
						if (dep == 0) opt_move = tuple(x1, y1, x2, y2);
					}
				}
			}
		}
	}
	if (flag == 0) {
		int res = -dfs(game, turn ^ 3, dep + 1, -beta, -alpha, opt_move);
		if (ret < res) {
			ret = res;
			if (dep == 0) opt_move = tuple(-1, -1, -1, -1);
		}
	}
	return ret;
}

다음 상태의 반환값을 재귀적으로 구할 때 -dfs(nxt, turn ^ 3, dep + 1, -beta, -alpha, opt_move)와 같이 alpha, beta의 인자로 $-\beta$와 $-\alpha$를 이용함에 주의해야 합니다.

Agent 1 (H1): test/abprun
Agent 2 (H0): test/minimax
Elo [H0, H1]: [0.0, 50.0] -> P [P0, P1]: [0.5000, 0.5715]
LLR bounds: [-2.944, 2.944] (Alpha=0.05, Beta=0.05)
LLR updates: Win=+0.1336, Loss=-0.1542, Draw=0.0

[SPRT Finished]
Total: 286, WLD: 143/143/0, LLR: -2.951 [-2.944, 2.944]
Final LLR: -2.951
Result: Accept H0. Agent 1 is likely not better (Elo <= 0.0).

Alpha-Beta Pruning은 Minimax Algorithm의 결과를 바꾸지 않으면서 실행 시간만 단축시켜주기 때문에 max_depth를 바꾸지 않은 위의 코드는 기존 Minimax Algorithm을 이용한 정책과 동일한 성능을 보입니다. 이때 시간 제한에 맞춰서 max_depth를 늘리는 경우 Alpha-Beta Pruning을 이용한 코드는 max_depth를 더 크게 설정할 수 있다는 장점이 있습니다.

8. Summary

이번 글에서는 $2$인, 제로섬, 턴제, 완전정보, 결정론적 게임인 ATAXX를 예시로 하여, 게임 에이전트의 기본적인 탐색 알고리즘을 단계별로 구현하고 발전시켜 보았습니다.

지금까지 살펴본 정책들은 다음과 같습니다.

Random Agent: 가장 먼저, 가능한 모든 수 중에서 무작위로 하나를 선택하는 랜덤 에이전트를 구현하여 알고리즘 성능 비교를 위한 기준선(Baseline)을 설정했습니다.
Greedy Agent: ‘돌의 개수 차이’라는 간단한 휴리스틱 평가 함수(Heuristic Evaluation Function)를 도입했습니다. 이를 이용해 $1$수 앞을 내다보고 현재 상태에서 평가값이 가장 높은 수를 선택하는 그리디 에이전트를 구현했습니다.
Minimax & Negamax Algorithm: $1$수 앞만 보는 그리디 정책의 한계를 넘어, 정해진 깊이까지 상대방의 최선의 대응을 고려하며 탐색하는 Minimax Algorithm을 알아보았습니다. 또한 $\min(a, b) = -\max(-b, -a)$ 관계를 이용해 Max/Min 노드의 로직을 통합, 코드를 간결하게 만든 Negamax 변형도 다루었습니다.
Alpha-Beta Pruning: 마지막으로, Minimax/Negamax 알고리즘이 탐색 트리의 최종 결과에 영향을 주지 않는 불필요한 분기를 탐색하는 비효율을 제거하는 Alpha-Beta Pruning(알파-베타 가지치기) 기법을 적용했습니다. 이를 이용하면 동일한 시간 내에 더 깊은 깊이를 탐색할 수 있습니다.

지금까지 다룬 기법들은 고전적이면서도 여전히 강력한 게임 탐색의 근간을 이룹니다. 이어지는 글에서는 MCTS(Monte Carlo Tree Search)와 같은 현대적인 탐색 기법을 알아보고, 신경망을 이용한 평가 함수(NNUE) 및 다양한 탐색 최적화 방법들을 살펴보겠습니다.

note. 이번 글에서 다룬 코드들은 여기에서 테스트해볼 수 있습니다.

References

[1] https://en.wikipedia.org/wiki/Ataxx

[2] https://en.wikipedia.org/wiki/Sequential_probability_ratio_test

[3] https://mattlapa.com/sprt/

Advanced Game Search Algorithms (1)

1. Introduction

2. ATAXX

2.1 게임 규칙

2.2 입출력 형식

3. Random Agent

4. Greedy Agent

5. SPRT(Sequential Probability Ratio Test)

6. Minimax Algorithm

6.1 Minimax Algorithm

6.2 Negamax Algorithm

7. Alpha-Beta Pruning

7.1 Alpha-Beta Pruning

7.2 Negamax-Style Alpha-Beta Pruning

8. Summary

References

Ladder Decomposition

A game of cops and robbers on planar graph