Advanced Game Search Algorithms (2)

algorithm , game-theory , problem-solving

1. Introduction

지난 Advanced Game Search Algorithms (1) 글에서는 Random, Greedy와 Minimax 에이전트들을 알아보았습니다.

이번 글에서는 Minimax 에이전트를 개선하는 Iterative Deepening 기법과 여러 Search Pruning 기법을 알아보겠습니다. 이는 주어진 탐색 시간을 더 효율적으로 사용하며 깊은 깊이까지 game tree를 탐색해 에이전트의 성능을 극적으로 개선합니다.

이번 글에서 다룬 코드들은 여기에서 테스트해볼 수 있습니다.

2. Baseline Code

이번 글에서 구현할 에이전트들은 게임 트리 탐색을 이용하기 때문에 많은 수의 노드를 확인할 수록 더 좋은 move를 선택할 수 있습니다. 그러므로 제한 시간 내에 최대한 많은 노드를 확인할 수 있도록 성능을 최적화하는 것이 필요합니다.

이를 위해 우선 move $(x_1, y_1, x_2, y_2)$를 효율적으로 표현하는 struct를 구현했습니다.

[expand Show 28 lines of code]

struct board_move {
	u16 data;
	board_move(u16 data) : data(data) {}
	board_move(int x1, int y1, int x2, int y2) {
		if (x1 == -1) { data = u16(-1); return; }
		data = u16(x1 * 7 + y1 - 8) << 6 | u16(x2 * 7 + y2 - 8);
		if (max(abs(x1 - x2), abs(y1 - y2)) == 2) data |= u16(1) << 12;
	}
	bool is_pass() const {
		return data == u16(-1);
	}
	bool is_jump() const {
		return data >> 12 & 1;
	}
	pair<int, int> get_ij() const {
		int i = data >> 6 & 63;
		int j = data & 63;
		return { i, j };
	}
	tuple<int, int, int, int> get_xy() const {
		if (is_pass()) return { -1, -1, -1, -1 };
		int x1 = (data >> 6 & 63) / 7 + 1;
		int y1 = (data >> 6 & 63) % 7 + 1;
		int x2 = (data & 63) / 7 + 1;
		int y2 = (data & 63) % 7 + 1;
		return { x1, y1, x2, y2 };
	}
};

[/expand]

board_move 자료형에서 데이터는 $16$비트 정수 자료형을 이용해 저장됩니다.

처음 $6$개 비트는 $(x_1 - 1) \cdot 7 + (y_1 - 1)$을 나타내며, 다음 $6$개 비트는 $(x_2 - 1) \cdot 7 + (y_2 - 1)$을 나타냅니다. 추가로 $1$개 비트를 사용해 $\max(\lvert x_1 - x_2 \rvert, \lvert y_1 - y_2 \rvert)$가 $2$인지 여부를 저장해 이후 연산을 board에 적용할 때 jump인지 여부를 빠르게 알 수 있도록 합니다.

pass는 $-1$을 이용해 표현했습니다.

다음은 보드의 상태를 저장하는 struct입니다.

[expand Show 73 lines of code]

int gen_rand(int l, int r) {
	static mt19937 rd(chrono::steady_clock::now().time_since_epoch().count());
	return uniform_int_distribution(l, r)(rd);
}

struct board_info {
	u64 mask1[49];
	u64 mask2[49];
	vector<int> nxt1[49];
	vector<int> nxt2[49];
	board_info() {
		for (int i = 0; i < 49; i++) {
			mask1[i] = 0;
			mask2[i] = 0;
			int x1 = i / 7, y1 = i % 7;
			for (int j = 0; j < 49; j++) {
				int x2 = j / 7, y2 = j % 7;
				int d = max(abs(x1 - x2), abs(y1 - y2));
				if (d == 1) nxt1[i].push_back(j), mask1[i] |= u64(1) << j, mask2[i] |= u64(1) << j;
				if (d == 2) nxt2[i].push_back(j), mask2[i] |= u64(1) << j;
			}
		}
	}
} info;

struct board {
	u64 a, b;
	board() : a(u64(1) | u64(1) << 48), b(u64(1) << 6 | u64(1) << 42) {}
	board(u64 a, u64 b) : a(a), b(b) {}
	void change_turn() {
		swap(a, b);
	}
	bool is_pass() const {
		for (int i = 0; i < 49; i++) {
			if (~a >> i & 1) continue;
			if (~(a | b) & info.mask2[i]) return false;
		}
		return true;
	}
	bool is_finish() const {
		if (a == 0 || b == 0) return true;
		if ((a | b) == (u64(1) << 49) - 1) return true;
		return false;
	}
	int eval() const {
		return __builtin_popcountll(a) - __builtin_popcountll(b);
	}
	void apply_move(board_move op) {
		if (op.is_pass()) return;
		auto [i, j] = op.get_ij();
		if (op.is_jump()) a &= ~(u64(1) << i);
		a = a | u64(1) << j | (b & info.mask1[j]);
		b = b & ~info.mask1[j];
	}
	vector<board_move> gen_move() const {
		vector<board_move> ret;
		for (int i = 0; i < 49; i++) {
			if (~a >> i & 1) continue;
			for (int j : info.nxt1[i]) {
				if ((a | b) >> j & 1) continue;
				ret.push_back(board_move(u16(i) << 6 | u16(j)));
			}
			for (int j : info.nxt2[i]) {
				if ((a | b) >> j & 1) continue;
				ret.push_back(board_move(u16(i) << 6 | u16(j) | u16(1 << 12)));
			}
		}
		for (int i = 1; i < ret.size(); i++) {
			swap(ret[i], ret[gen_rand(0, i)]);
		}
		return ret;
	}
};

[/expand]

board 자료형은 내부적으로 64비트 정수 자료형 $a$, $b$를 이용해 내가 점유한 칸과 상대가 점유한 칸을 관리합니다.

세부적인 구현 사항은 다음과 같습니다.

change_turn: swap(a, b)로 턴을 바꿉니다.
is_pass: 가능한 move가 있다면 false, 아니라면 true를 반환합니다.
is_finish: $a$ 또는 $b$가 $0$이거나, 남은 빈 칸이 하나도 없다면 true, 아니라면 false를 반환합니다.
eval: 내가 점유한 칸의 개수에서 상대가 점유한 칸의 개수를 뺀 값을 반환합니다.
apply_move: board_move 자료형으로 move를 입력받아서 $a$, $b$에 연산을 수행합니다.
gen_move: 가능한 move의 리스트를 vector<board_move> 자료형으로 반환합니다. 결과는 무작위로 셔플해서 반환합니다.

board_move와 마찬가지로 board 자료형은 비트 연산을 이용해 최적화해서 구현했습니다. is_pass, apply_move, gen_move 함수에서 중복해서 사용하는 bitmask나 인덱스 집합은 board_info를 이용해 전처리를 한 뒤 사용했습니다.

다음은 이번 글의 baseline이 될 board_move, board 자료형을 이용한 Minimax 에이전트 코드입니다.

[expand Show 176 lines of code]

#include <bits/stdc++.h>
using namespace std;

using u64 = unsigned long long;
using u16 = unsigned short;

constexpr int inf = 1 << 30;

int gen_rand(int l, int r) {
	static mt19937 rd(chrono::steady_clock::now().time_since_epoch().count());
	return uniform_int_distribution(l, r)(rd);
}

struct board_move {
	u16 data;
	board_move(u16 data) : data(data) {}
	board_move(int x1, int y1, int x2, int y2) {
		if (x1 == -1) { data = u16(-1); return; }
		data = u16(x1 * 7 + y1 - 8) << 6 | u16(x2 * 7 + y2 - 8);
		if (max(abs(x1 - x2), abs(y1 - y2)) == 2) data |= u16(1) << 12;
	}
	bool is_pass() const {
		return data == u16(-1);
	}
	bool is_jump() const {
		return data >> 12 & 1;
	}
	pair<int, int> get_ij() const {
		int i = data >> 6 & 63;
		int j = data & 63;
		return { i, j };
	}
	tuple<int, int, int, int> get_xy() const {
		if (is_pass()) return { -1, -1, -1, -1 };
		int x1 = (data >> 6 & 63) / 7 + 1;
		int y1 = (data >> 6 & 63) % 7 + 1;
		int x2 = (data & 63) / 7 + 1;
		int y2 = (data & 63) % 7 + 1;
		return { x1, y1, x2, y2 };
	}
};

struct board_info {
	u64 mask1[49];
	u64 mask2[49];
	vector<int> nxt1[49];
	vector<int> nxt2[49];
	board_info() {
		for (int i = 0; i < 49; i++) {
			mask1[i] = 0;
			mask2[i] = 0;
			int x1 = i / 7, y1 = i % 7;
			for (int j = 0; j < 49; j++) {
				int x2 = j / 7, y2 = j % 7;
				int d = max(abs(x1 - x2), abs(y1 - y2));
				if (d == 1) nxt1[i].push_back(j), mask1[i] |= u64(1) << j, mask2[i] |= u64(1) << j;
				if (d == 2) nxt2[i].push_back(j), mask2[i] |= u64(1) << j;
			}
		}
	}
} info;

struct board {
	u64 a, b;
	board() : a(u64(1) | u64(1) << 48), b(u64(1) << 6 | u64(1) << 42) {}
	board(u64 a, u64 b) : a(a), b(b) {}
	void change_turn() {
		swap(a, b);
	}
	bool is_pass() const {
		for (int i = 0; i < 49; i++) {
			if (~a >> i & 1) continue;
			if (~(a | b) & info.mask2[i]) return false;
		}
		return true;
	}
	bool is_finish() const {
		if (a == 0 || b == 0) return true;
		if ((a | b) == (u64(1) << 49) - 1) return true;
		return false;
	}
	int eval() const {
		return __builtin_popcountll(a) - __builtin_popcountll(b);
	}
	void apply_move(board_move op) {
		if (op.is_pass()) return;
		auto [i, j] = op.get_ij();
		if (op.is_jump()) a &= ~(u64(1) << i);
		a = a | u64(1) << j | (b & info.mask1[j]);
		b = b & ~info.mask1[j];
	}
	vector<board_move> gen_move() const {
		vector<board_move> ret;
		for (int i = 0; i < 49; i++) {
			if (~a >> i & 1) continue;
			for (int j : info.nxt1[i]) {
				if ((a | b) >> j & 1) continue;
				ret.push_back(board_move(u16(i) << 6 | u16(j)));
			}
			for (int j : info.nxt2[i]) {
				if ((a | b) >> j & 1) continue;
				ret.push_back(board_move(u16(i) << 6 | u16(j) | u16(1 << 12)));
			}
		}
		for (int i = 1; i < ret.size(); i++) {
			swap(ret[i], ret[gen_rand(0, i)]);
		}
		return ret;
	}
};

board_move minimax(board game, int lim) {
	board_move opt(u16(0));
	auto rec = [&](const auto& self, board cur, int dep) -> int {
		if (cur.is_finish()) {
			return cur.eval() > 0 ? inf - dep : -inf + dep;
		}
		if (dep == lim) {
			return cur.eval();
		}
		if (cur.is_pass()) {
			board nxt = cur;
			nxt.change_turn();
			return -self(self, nxt, dep + 1);
		}
		int ret = -inf;
		for (board_move op : cur.gen_move()) {
			board nxt = cur;
			nxt.apply_move(op);
			nxt.change_turn();
			int res = -self(self, nxt, dep + 1);
			if (ret < res) { ret = res; if (dep == 0) opt = op; }
		}
		return ret;
	};
	rec(rec, game, 0);
	return opt;
}

board_move find_move(board game, int t1, int t2) {
	if (game.is_pass()) return board_move(u16(-1));
	return minimax(game, 3);
}

int main() {
	board game;
	while (1) {
		string s; getline(cin, s);
		istringstream in(s);
		string cmd; in >> cmd;
		if (cmd == "READY") {
			string t; in >> t;
			if (t == "SECOND") game.change_turn();
			cout << "OK" << endl;
		}
		else if (cmd == "TURN") {
			int t1, t2; in >> t1 >> t2;
			auto op = find_move(game, t1, t2);
			auto [x1, y1, x2, y2] = op.get_xy();
			game.apply_move(board_move(x1, y1, x2, y2));
			cout << "MOVE " << x1 << ' ' << y1 << ' ' << x2 << ' ' << y2 << endl;
		}
		else if (cmd == "OPP") {
			int x1, y1, x2, y2, t2; in >> x1 >> y1 >> x2 >> y2 >> t2;
			game.change_turn();
			game.apply_move(board_move(x1, y1, x2, y2));
			game.change_turn();
		}
		else if (cmd == "FINISH") {
			break;
		}
		else {
			assert(0);
		}
	}
}

[/expand]

이상으로 깊이 제한이 $3$인 Negamax-Style의 Minimax 에이전트를 효율적으로 구현했습니다.

이후 구현하는 모든 코드는 기본적으로 baseline과의 비교를 수행합니다.

3. Alpha-Beta Pruning

Minimax 에이전트를 개선하는 가장 대표적이면서 효과적인 방법은 이전 글에서 소개한 Alpha-Beta Pruning입니다. 이번 글에서는 baseline이 바뀌었으니, 복습 겸 다시 간단히 코드를 살펴봅시다.

board_move ab_prun(board game, int lim) {
	board_move opt(u16(0));
	auto rec = [&](const auto& self, board cur, int dep, int alpha, int beta) -> int {
		if (cur.is_finish()) {
			return cur.eval() > 0 ? inf - dep : -inf + dep;
		}
		if (dep == lim) {
			return cur.eval();
		}
		if (cur.is_pass()) {
			board nxt = cur;
			nxt.change_turn();
			return -self(self, nxt, dep + 1, -beta, -alpha);
		}
		int ret = -inf;
		for (board_move op : cur.gen_move()) {
			board nxt = cur;
			nxt.apply_move(op);
			nxt.change_turn();
			int res = -self(self, nxt, dep + 1, -beta, -alpha);
			if (ret < res) { ret = res; if (dep == 0) opt = op; }
			if (alpha < res) alpha = res;
			if (alpha >= beta) return alpha;
		}
		return ret;
	};
	rec(rec, game, 0, -inf, inf);
	return opt;
}

Negamax-Style Minimax Algorithm에서 조상 노드에서 현재 플레이어가 얻은 반환값의 최댓값을 $\alpha$, 상대 플레이어가 얻은 반환값의 최솟값을 $\beta$로 관리하면 $\alpha \ge \beta$가 되는 시점에 가지치기를 적용할 수 있었습니다.

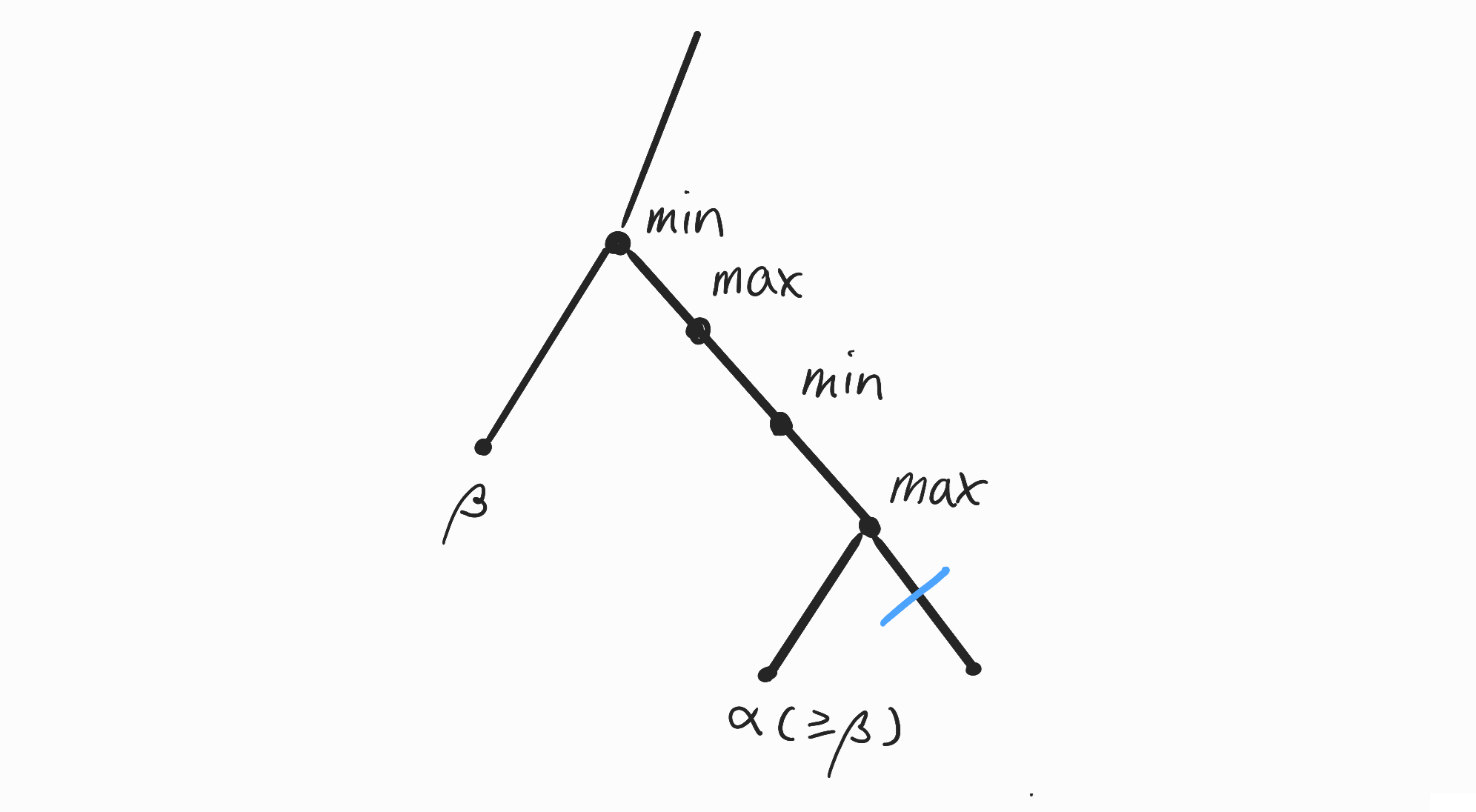
이유는 현재 반환값이 $\beta$ 이상이 된다면 조상 노드 중 $\beta$를 얻은 상대 플레이어는 현재 보고있는 노드 쪽으로 game tree를 호출하지 않을 것이기 때문입니다.

이를 이용하면 Alpha-Beta Pruning을 이용해 Minimax Algorithm과 동일한 결과를 더 빠르게 구할 수 있습니다.

Agent 1 (H1): test/abprun
Agent 2 (H0): test/base

...

agent2(X) WINS 27-22 | T78 | A1 104ms / A2 592ms
Total: 433, WLD: 222/211/0, LLR: -2.885 [-2.944, 2.944]

agent2(O) WINS 30-19 | T99 | A1 127ms / A2 1313ms
Total: 434, WLD: 222/212/0, LLR: -3.040 [-2.944, 2.944]

[SPRT Finished]
Total: 434, WLD: 222/212/0, LLR: -3.040 [-2.944, 2.944]
Final LLR: -3.040
Result: Accept H0. Agent 1 is likely not better (Elo <= 0.0).

Alpha-Beta Pruning을 적용한 코드와 Baseline을 SPRT로 비교 검증한 결과는 위와 같습니다. 두 모델은 동일한 평가 로직을 공유하므로 이론상 실력 차이가 없으나, 앞서 언급한 무작위 셔플의 영향으로 $51:49$ 정도의 미세한 승률 차이가 발생했습니다.

그러나 SPRT는 LLR(Log-Likelihood Ratio)이 임계값인 $-2.944$ 미만으로 하락하는 시점에 두 에이전트의 성능 차이가 없다는 올바른 결론을 반환합니다. 추가로 로그를 분석해보면 Pruning을 이용한 코드가 baseline보다 $5\sim10$배가량 빠르게 동작하는 걸 알 수 있습니다.

4. Iterative Deepening

지금까지 구현한 Minimax 또는 Alpha-Beta Pruning 코드는 최대 깊이 제한인 max_depth를 $3$으로 두고, 탐색이 최대 깊이에 도달한다면 eval 함수를 이용해 노드의 평가치를 바로 반환합니다.

Iterative Deepening 기법은 max_depth를 순차적으로 늘리며 현재 제한 시간을 만족하는 가능한 큰 max_depth를 구하는 기법입니다.

다음은 Alpha-Beta Pruning 코드에 Iterative Deepening을 적용한 코드입니다.

pair<int, board_move> ab_prun(board game, int lim, const auto& is_timeout) {
	board_move opt(u16(0));
	auto rec = [&](const auto& self, board cur, int dep, int alpha, int beta) -> int {
		if (is_timeout()) return 0;
		if (cur.is_finish()) {
			return cur.eval() > 0 ? inf - dep : -inf + dep;
		}
		if (dep == lim) {
			return cur.eval();
		}
		if (cur.is_pass()) {
			board nxt = cur;
			nxt.change_turn();
			return -self(self, nxt, dep + 1, -beta, -alpha);
		}
		int ret = -inf;
		for (board_move op : cur.gen_move()) {
			if (is_timeout()) return 0;
			board nxt = cur;
			nxt.apply_move(op);
			nxt.change_turn();
			int res = -self(self, nxt, dep + 1, -beta, -alpha);
			if (ret < res) { ret = res; if (dep == 0) opt = op; }
			if (alpha < res) alpha = res;
			if (alpha >= beta) return alpha;
		}
		return ret;
	};
	int val = rec(rec, game, 0, -inf, inf);
	return pair(val, opt);
}

board_move find_move(board game, int t1, int t2) {
	if (game.is_pass()) return board_move(u16(-1));
	int timeout_ms = 150;
	if (t1 - timeout_ms < 1000) timeout_ms = 10;
	auto deadline = chrono::steady_clock::now() + chrono::milliseconds(timeout_ms);
	auto is_timeout = [&] { return chrono::steady_clock::now() >= deadline; };
	board_move ret(u16(0));
	for (int lim = 1; ; lim++) {
		auto [val, res] = ab_prun(game, lim, is_timeout);
		if (is_timeout()) break;
		ret = res;
		if (val <= -inf + 800 || inf - 800 <= val) break;
	}
	return ret;
}

구현은 max_depth를 $1$씩 증가시키며 수행하되, chrono::steady_clock을 사용하여 timeout_ms가 경과하면 즉시 중단하도록 설계했습니다.

시간 초과로 탐색이 중단된 경우 해당 깊이의 결과는 신뢰할 수 없으므로, 이전 max_depth에서 구했던 해를 최종 결과로 사용합니다. 또한, ab_prun 함수의 반환 타입을 pair<int, board_move>로 변경하여 평가 점수도 함께 반환받도록 수정했습니다. 만약 반환된 점수가 inf나 -inf에 근접한 값이라면(즉, 승패가 확정된 경우), 더 깊이 탐색하더라도 결과가 바뀌지 않으므로 즉시 반복문을 종료하여 불필요한 연산을 방지했습니다.

이렇게 max_depth를 순차적으로 늘려주는 방식은 탐색 시간이 충분히 주어지는 경우에는 더 좋은 수를 찾을 것이고, 그렇지 않은 경우에는 제한 시간 내에서 valid한 move를 골라 시간 초과를 방지할 것입니다.

코드에서 현재 턴에 사용할 시간 제한은 남은 시간이 $1000$ ms 이상이라면 $150$ ms로, 그렇지 않다면 $10$ ms로 설정했습니다. 이 글에 등장하는 모든 에이전트는 이와 동일한 시간 관리 전략이 적용됩니다. 시간 배분은 선택하는 move의 품질에 결정적인 영향을 미치므로, 초반, 중반, 후반부로 나누어 시간을 다르게 배분하는 등 더 정교한 전략을 도입한다면 성능을 더욱 개선할 수 있을 것입니다.

Agent 1 (H1): test/idab
Agent 2 (H0): test/base

[SPRT Finished]
Total: 27, WLD: 25/2/0, LLR: 3.031 [-2.944, 2.944]
Final LLR: 3.031
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

Iterative Deepening을 적용한 Alpha-Beta Pruning 코드를 baseline과 비교한 결과는 위와 같습니다.

note. Iterative Deepening 자체는 탐색하는 노드의 수를 줄여주지 않지만, 다음 장에서 다룰 Transposition Table과 결합될 때 Move Ordering을 통해 Alpha-Beta Pruning의 효율을 크게 늘리며 추가적인 성능 향상을 보입니다.

5. Transposition Table

전치표^{Transposition Table}은 탐색 과정에서 얻은 정보를 저장해두는 해시 테이블^{hash table}입니다. 게임 트리 탐색을 하다 보면 서로 다른 수순을 거쳤더라도 결과적으로 동일한 보드 상태^{transposition}에 도달하는 경우가 빈번합니다. 이때 이전 탐색 결과를 저장해두었다가 재사용하면 중복 계산을 줄이고 탐색 효율을 비약적으로 높일 수 있습니다.

이 기법은 크게 두 가지 상황에서 탐색 효율을 비약적으로 높여줍니다.

Move Ordering: 이전 탐색에서 찾은 최적의 수를 현재 탐색에서도 가장 먼저 확인하도록 순서를 조정합니다. 이는 Iterative Deepening을 사용하는 Alpha-Beta Pruning 탐색의 효율을 극대화합니다.
TT Cutoff: 이전에 충분히 깊은 깊이까지 탐색해 둔 결과가 있다면 다시 계산하지 않고 그 값을 바로 반환합니다. 이는 중복 탐색을 막아 탐색 효율을 높입니다.

5.1 Hash Function

전치표를 구현하기 위해서는 우선 보드의 상태를 고유한 정수로 변환하는 해시 함수가 필요합니다.

struct board {
	u64 a, b;
	u64 xorshift(u64 x) const {
		x ^= x << 13;
		x ^= x >> 7;
		x ^= x << 17;
		return x;
	}
	u64 get_hash() const {
		u64 x = 0x814814;
		x += a;
		x = xorshift(x);
		x = xorshift(x);
		x += b;
		x = xorshift(x);
		x = xorshift(x);
		return x;
	}
	// ...
};

get_hash는 board 내부의 $a$와 $b$를 비트 연산으로 섞어 64비트 해시값을 생성하는 함수입니다.

해시 함수는 계산 비용과 품질을 고려해 zobrist hashing 등의 다른 함수로 대체할 수 있습니다. 이 글에서는 해시 함수로 빠른 계산 속도와 적당한 충돌 확률을 갖는 xorshift의 변형을 사용합니다.

5.2 Move Ordering

전치표를 이용한 첫 번째 최적화 기법은 Move Ordering입니다.

Iterative Deepening의 이전 깊이나 이전 턴에서 찾은 move를 현재 탐색에서 가장 먼저 사용하도록 하면 가능한 move 중 좋은 move를 먼저 탐색할 확률이 높아집니다. 이는 Alpha-Beta Pruning 과정에서 더 큰 반환값을 빠르게 찾도록 해서 $\alpha \ge \beta$ 조건을 이용하는 pruning의 효율을 높입니다.

Move Ordering을 지원하기 위해서는 아래와 같이 전치표를 먼저 구성해야 합니다.

constexpr int tt_sz = 4'000'000;

struct tt_node {
	u64 h;
	board_move op;
	tt_node() : h{}, op(u16(0)) {}
} tt[tt_sz];

전치표는 tt_sz개의 tt_node로 구성됩니다. tt_node는 해당 상태의 해시값 h와 그 상태에서 가장 좋았던 수 op를 저장합니다.

전치표를 이용하면 다음과 같이 Move Ordering을 구현할 수 있습니다.

pair<int, board_move> ab_prun(board game, int lim, const auto& is_timeout) {
	board_move opt(u16(0));
	auto rec = [&](const auto& self, board cur, int dep, int alpha, int beta) -> int {
		if (is_timeout()) return 0;
		if (cur.is_finish()) {
			return cur.eval() > 0 ? inf - dep : -(inf - dep);
		}
		if (dep == lim) {
			return cur.eval();
		}
		if (cur.is_pass()) {
			board nxt = cur;
			nxt.change_turn();
			return -self(self, nxt, dep + 1, -beta, -alpha);
		}
		u64 h = cur.get_hash();
		tt_node& tt_data = tt[h % tt_sz];
		vector<board_move> cand = cur.gen_move();
		if (tt_data.h == h) {
			for (int i = 0; i < cand.size(); i++) {
				if (cand[i].data != tt_data.op.data) continue;
				swap(cand[0], cand[i]);
				break;
			}
		}
		int ret = -inf;
		board_move copt(0);
		for (board_move op : cand) {
			if (is_timeout()) return 0;
			board nxt = cur;
			nxt.apply_move(op);
			nxt.change_turn();
			int res = -self(self, nxt, dep + 1, -beta, -alpha);
			if (ret < res) ret = res, copt = op;
			if (alpha < res) alpha = res;
			if (alpha >= beta) break;
		}
		if (dep == 0) opt = copt;
		tt_data.h = h;
		tt_data.op = copt;
		return ret;
	};
	int val = rec(rec, game, 0, -inf, inf);
	return pair(val, opt);
}

코드는 전치표에서 해시값을 tt_sz로 나눈 나머지에 해당하는 tt_node를 이용해 Move Ordering을 수행합니다.

이때 tt_node.h == h 조건을 통해 해시값이 일치하는지 확인해야 합니다. 이는 인덱스가 같더라도 실제 보드 상태가 다를 수 있기 때문입니다. 해시값까지 우연히 같을 확률은 무시할 만큼 낮기에 만약 충돌이 발생하더라도 성능에 미치는 영향은 매우 작다고 가정합니다.

탐색 루프가 종료되면 최종적으로 구한 최적해를 전치표에 기록합니다.

Agent 1 (H1): test/ttmo
Agent 2 (H0): test/base

[SPRT Finished]
Total: 25, WLD: 24/1/0, LLR: 3.052 [-2.944, 2.944]
Final LLR: 3.052
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

Agent 1 (H1): test/ttmo
Agent 2 (H0): test/idab

[SPRT Finished]
Total: 57, WLD: 41/16/0, LLR: 3.010 [-2.944, 2.944]
Final LLR: 3.010
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

전치표와 Move Ordering을 적용한 코드와 baseline, Iterative Deepening 코드를 비교한 결과는 위와 같습니다.

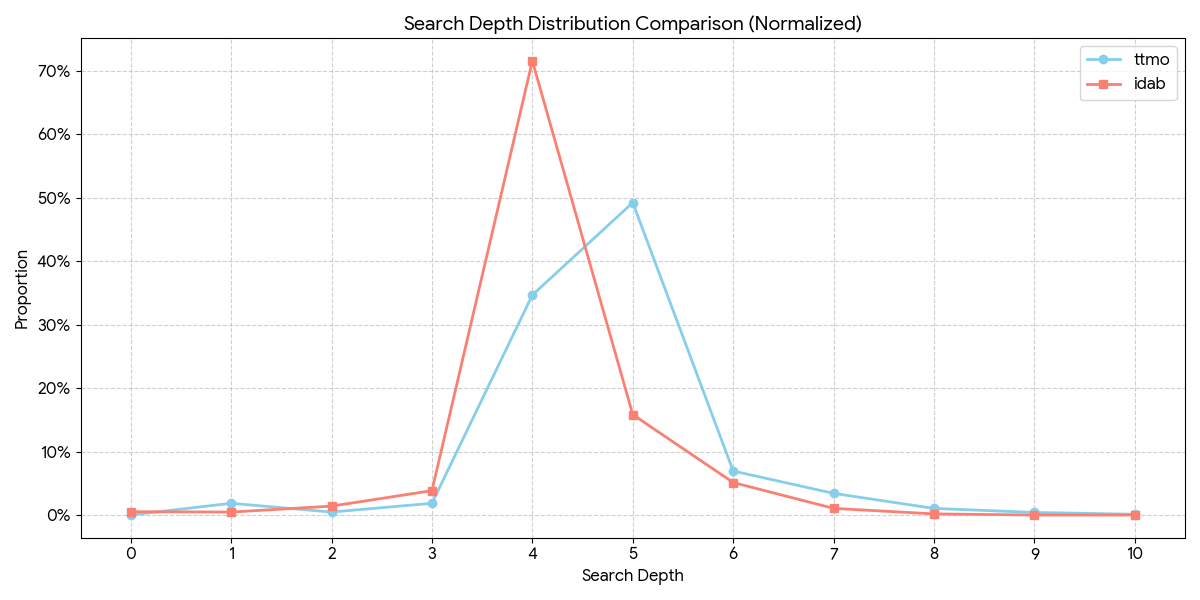
$150$ ms 제한에서 두 코드가 Iterative Deepening 과정에서 사용하는 최대 깊이를 그래프로 그려보면 실제로 전치표를 이용할 때가 최대 깊이가 늘어나는 걸 알 수 있습니다.

이는 Move Ordering이 실제로 Alpha-Beta Pruning에서 가지치기 효율을 높여 더 깊은 깊이까지 탐색을 가능하게 한다는 걸 의미합니다.

5.3 TT Cutoff

전치표를 이용한 두 번째 최적화 기법은 TT Cutoff입니다.

Move Ordering이 탐색의 순서를 최적화하여 가지치기 확률을 높여준다면, TT Cutoff는 이미 탐색한 결과를 재사용하여 탐색 자체를 생략하는 기법입니다. 만약 현재 도달한 보드 상태를 이전에 현재 깊이 이상으로 탐색한 기록이 있고, 그 결과가 현재의 $\alpha$, $\beta$ 범위 내에서 유효하다면, 저장된 값을 즉시 반환할 수 있습니다.

이를 구현하기 위해서는 tt_node에 노드의 타입 flag, 평가 점수 val, 탐색 깊이 dep을 추가로 저장해야 합니다.

enum tt_flag {
	PV_NODE,
	CUT_NODE,
	ALL_NODE
};

노드의 타입은 PV_NODE, CUT_NODE, ALL_NODE $3$가지로 나뉩니다.

PV_NODE는 이전에 해당 상태를 방문했을 때 구한 반환값 $x$가 초기 $\alpha$, $\beta$에 대해 $\alpha < x < \beta$를 만족했음을 의미합니다. 이는 현재 노드가 기존 값보다 좋은 값을 반환하면서 $\beta$에 의해 cutoff되지 않은 해당 시점에서 최적의 노드였음을 의미합니다. CUT_NODE는 $x \ge \beta$를 만족해 cutoff된 노드를 의미합니다. 이때 $x$값은 game tree를 모두 탐색하기 전에 cutoff되었기 때문에 실제 값보다 작을 수 있습니다. 마지막으로 ALL_NODE는 $x \le \alpha$를 만족한 경우로 game tree를 모두 탐색했지만 더 좋은 값을 구하지 못했음을 의미합니다.

struct tt_node {
	u64 h;
	board_move op;
	tt_flag flag;
	int dep;
	int val;
	tt_node() : h{}, op(u16(0)), flag(PV_NODE), dep(-1), val(0) {}
	void set_val(int x, int dep) {
		if (x <= -inf + 800) val = x - dep;
		else if (x >= inf - 800) val = x + dep;
		else val = x;
	}
	int get_val(int dep) const {
		if (val <= -inf + 800) return val + dep;
		else if (val >= inf - 800) return val - dep;
		else return val;
	}
} tt[tt_sz];

flag, dep, val을 추가한 tt_node 코드는 위와 같습니다.

이때 set_val, get_val은 반환한 값이 inf에 가까운 값일 때 최대한 빠른 승리와 늦은 패배를 고르도록 하기 위해 정규화를 수행합니다.

이를 이용해 TT Cutoff를 적용한 코드는 다음과 같습니다.

pair<int, board_move> ab_prun(board game, int lim, const auto& is_timeout) {
	board_move opt(u16(0));
	auto rec = [&](const auto& self, board cur, int dep, int alpha, int beta) -> int {
		if (is_timeout()) return 0;
		if (cur.is_finish()) {
			return cur.eval() > 0 ? inf - dep : -(inf - dep);
		}
		if (dep == lim) {
			return cur.eval();
		}
		if (cur.is_pass()) {
			board nxt = cur;
			nxt.change_turn();
			return -self(self, nxt, dep + 1, -beta, -alpha);
		}
		u64 h = cur.get_hash();
		tt_node& tt_data = tt[h % tt_sz];
		// TT Cutoff
		if (dep > 0 && tt_data.h == h && tt_data.dep >= lim - dep) {
			if (tt_data.flag == PV_NODE) return tt_data.get_val(dep);
			if (tt_data.flag == CUT_NODE && tt_data.get_val(dep) >= beta) return tt_data.get_val(dep);
			if (tt_data.flag == ALL_NODE && tt_data.get_val(dep) <= alpha) return tt_data.get_val(dep);
		}
		// Move Ordering
		vector<board_move> cand = cur.gen_move();
		if (tt_data.h == h) {
			for (int i = 0; i < cand.size(); i++) {
				if (cand[i].data != tt_data.op.data) continue;
				swap(cand[0], cand[i]);
				break;
			}
		}
		int ret = -inf;
		int prv_alpha = alpha;
		board_move copt(0);
		for (board_move op : cand) {
			if (is_timeout()) return 0;
			board nxt = cur;
			nxt.apply_move(op);
			nxt.change_turn();
			int res = -self(self, nxt, dep + 1, -beta, -alpha);
			if (ret < res) ret = res, copt = op;
			if (alpha < res) alpha = res;
			if (alpha >= beta) break;
		}
		if (dep == 0) opt = copt;
		if (tt_data.h != h || tt_data.dep <= lim - dep) {
			tt_data.h = h;
			tt_data.op = copt;
			tt_data.flag = ret <= prv_alpha ? ALL_NODE : ret >= beta ? CUT_NODE : PV_NODE;
			tt_data.dep = lim - dep;
			tt_data.set_val(ret, dep);
		}
		return ret;
	};
	int val = rec(rec, game, 0, -inf, inf);
	return pair(val, opt);
}

TT Cutoff를 적용할 때는 몇 가지 주의사항이 있습니다. 먼저 루트 노드 dep == 0에서는 최적의 수를 갱신해야 하므로 Cutoff를 수행하지 않습니다. 또한 전치표에 저장된 탐색 깊이가 현재 남은 깊이보다 얕다면 정보의 신뢰도가 낮으므로 역시 Cutoff를 적용하지 않습니다. 나머지 경우는 flag를 확인하며 가능하다면 TT Cutoff를 적용해 바로 이전에 구한 값을 반환합니다.

또한, 전치표의 데이터 갱신 전략을 Depth-Based 방식으로 변경하였습니다. 단순히 최신 데이터로 덮어쓰는 것이 아니라, tt_data.dep <= lim - dep 조건이 성립할 때만 갱신하며 더 얕은 깊이의 정보로 깊은 깊이의 정보를 덮어쓰는 경우를 방지했습니다.

이를 기존 코드와 비교한 결과는 다음과 같습니다.

Agent 1 (H1): test/ttco
Agent 2 (H0): test/base

[SPRT Finished]
Total: 25, WLD: 24/1/0, LLR: 3.052 [-2.944, 2.944]
Final LLR: 3.052
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

Agent 1 (H1): test/ttco
Agent 2 (H0): test/idab

[SPRT Finished]
Total: 61, WLD: 43/18/0, LLR: 2.968 [-2.944, 2.944]
Final LLR: 2.968
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

Agent 1 (H1): test/ttco
Agent 2 (H0): test/ttmo

[SPRT Finished]
Total: 366, WLD: 186/180/0, LLR: -2.914 [-2.944, 2.944]
Final LLR: -3.068
Result: Accept H0. Agent 1 is likely not better (Elo <= 0.0).x

baseline, Iterative Deepening 코드와의 비교는 Move Ordering만 적용한 코드와 비슷한 성능을 보였습니다.

Move Ordering만 적용한 코드와의 비교는 $50$ elo 차이에 해당하는 유의미한 성능 개선을 보이지 않았습니다. 이는 평균적인 탐색 깊이가 $4 \sim 5$로 깊지 않아서 TT Cutoff가 줄이는 탐색 시간을 TT Cutoff 구현의 오버헤드가 상쇄시키기 때문이라 생각됩니다.

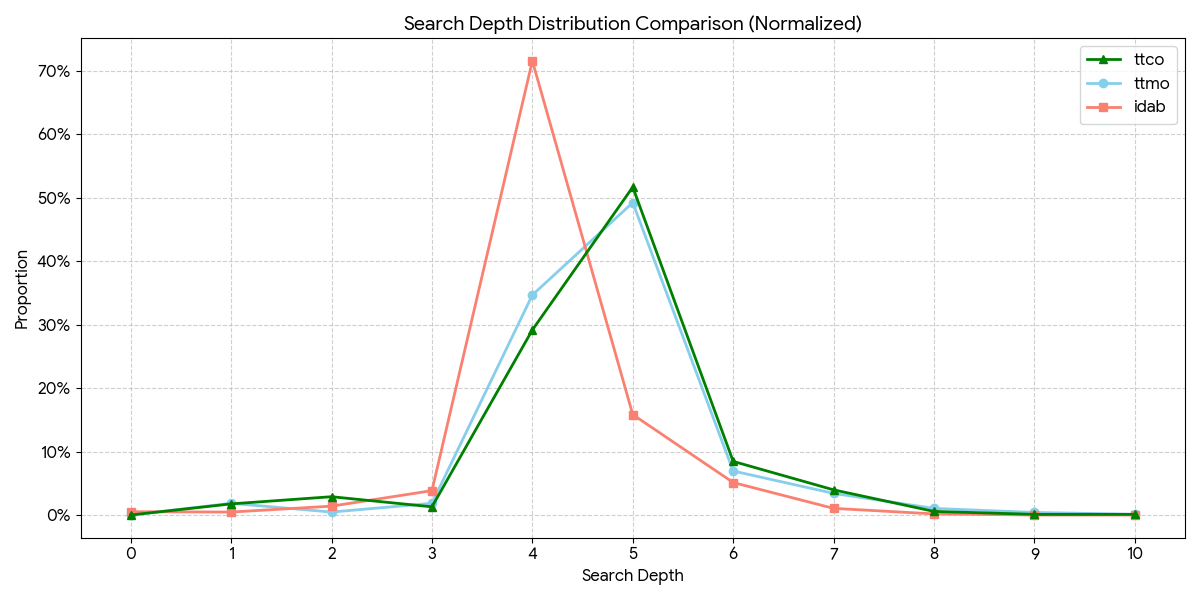
그래프를 보면 Move Ordering만 적용한 ttmo.cpp 코드와 TT Cutoff를 같이 적용한 ttco.cpp 코드 모두 평균적인 탐색 깊이가 $5$ 정도임을 알 수 있습니다.

6. Principal Variation Search

Alpha-Beta Pruning은 탐색 공간을 줄여주지만, 여전히 개선의 여지가 남아 있습니다. PVS^{Principal Variation Search}는 Alpha-Beta Pruning을 더 최적화한 알고리즘입니다.

PVS는 우리가 Move Ordering을 잘 수행했다면, 첫 번째로 확인하는 수가 최선의 수(PV, Principal Variation)일 것이란 가정을 이용합니다. 만약 첫 번째 수가 실제로 최선이라면, 나머지 수들은 첫 번째 수보다 나쁘다는 것만 증명하면 됩니다.

이를 위해 PVS는 첫 번째가 아닌 수에서 Null Window라고 불리는 아주 좁은 탐색 범위를 사용합니다. 일반적인 탐색이 $(\alpha, \beta)$ 범위를 사용한다면, Null Window는 $(\alpha, \alpha+1)$ 범위를 사용합니다. 이는 $\beta$ 대신 더 작은 값을 이용해 추가적인 Cutoff가 가능하도록 합니다.

구현 코드는 다음과 같습니다. 전치표를 이용한 TT Cutoff는 적용하지 않았습니다.

pair<int, board_move> pvs(board game, int lim, const auto& is_timeout) {
	board_move opt(u16(0));
	auto rec = [&](const auto& self, board cur, int dep, int alpha, int beta) -> int {
		if (is_timeout()) return 0;
		if (cur.is_finish()) {
			return cur.eval() > 0 ? inf - dep : -(inf - dep);
		}
		if (dep == lim) {
			return cur.eval();
		}
		if (cur.is_pass()) {
			board nxt = cur;
			nxt.change_turn();
			return -self(self, nxt, dep + 1, -beta, -alpha);
		}
		u64 h = cur.get_hash();
		tt_node& tt_data = tt[h % tt_sz];
		vector<board_move> cand = cur.gen_move();
		if (tt_data.h == h) {
			for (int i = 0; i < cand.size(); i++) {
				if (cand[i].data != tt_data.op.data) continue;
				swap(cand[0], cand[i]);
				break;
			}
		}
		int ret = -inf;
		board_move copt(0);
		for (int i = 0; i < cand.size(); i++) {
			if (is_timeout()) return 0;
			board_move op = cand[i];
			board nxt = cur;
			nxt.apply_move(op);
			nxt.change_turn();
			// PVS
			int nxt_alpha = i ? -alpha - 1 : -beta;
			int res = -self(self, nxt, dep + 1, nxt_alpha, -alpha);
			if (i && alpha < res && res < beta) {
				res = -self(self, nxt, dep + 1, -beta, -alpha);
			}
			if (ret < res) ret = res, copt = op;
			if (alpha < res) alpha = res;
			if (alpha >= beta) break;
		}
		if (dep == 0) opt = copt;
		tt_data.h = h;
		tt_data.op = copt;
		return ret;
	};
	int val = rec(rec, game, 0, -inf, inf);
	return pair(val, opt);
}

PVS에서 첫 번째 수는 Full Window $(\alpha, \beta)$를 이용해 탐색을 진행합니다. 나머지 수는 Null Window $(\alpha, \alpha + 1)$을 이용해 빠르게 확인한 뒤, $\alpha$보다 좋은 값을 찾았다면 다시 Full Window로 재탐색을 해줍니다.

PVS가 Alpha-Beta Pruning보다 빠르게 동작하기 위해선 첫 번째로 확인하는 수가 충분히 좋은 수여야 합니다. 만약 첫 번째 수가 최선이 아니라면 PVS는 재탐색으로 인해 오히려 더 느리게 동작할 수도 있습니다. 이후에도 Null Window에서 사용하는 $\alpha$ 값이 크다면 Cutoff가 더 많이 일어날 것이기 때문에 좋은 수를 먼저 확인할 수록 더 많은 개선을 얻을 수 있습니다.

따라서 PVS를 이용하기 위해선 전치표 등을 이용한 Move Ordering이 필수적입니다.

Agent 1 (H1): test/pvs
Agent 2 (H0): test/base

[SPRT Finished]
Total: 23, WLD: 23/0/0, LLR: 3.073 [-2.944, 2.944]
Final LLR: 3.073
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

Agent 1 (H1): test/pvs
Agent 2 (H0): test/idab

[SPRT Finished]
Total: 40, WLD: 32/8/0, LLR: 3.041 [-2.944, 2.944]
Final LLR: 3.041
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

Agent 1 (H1): test/pvs
Agent 2 (H0): test/ttmo

[SPRT Finished]
Total: 61, WLD: 43/18/0, LLR: 2.968 [-2.944, 2.944]
Final LLR: 2.968
Result: Accept H1. Agent 1 is likely better (Elo >= 50.0).

기존 코드와의 비교 결과는 PVS를 이용하는 경우가 더 좋은 성능을 보였습니다.

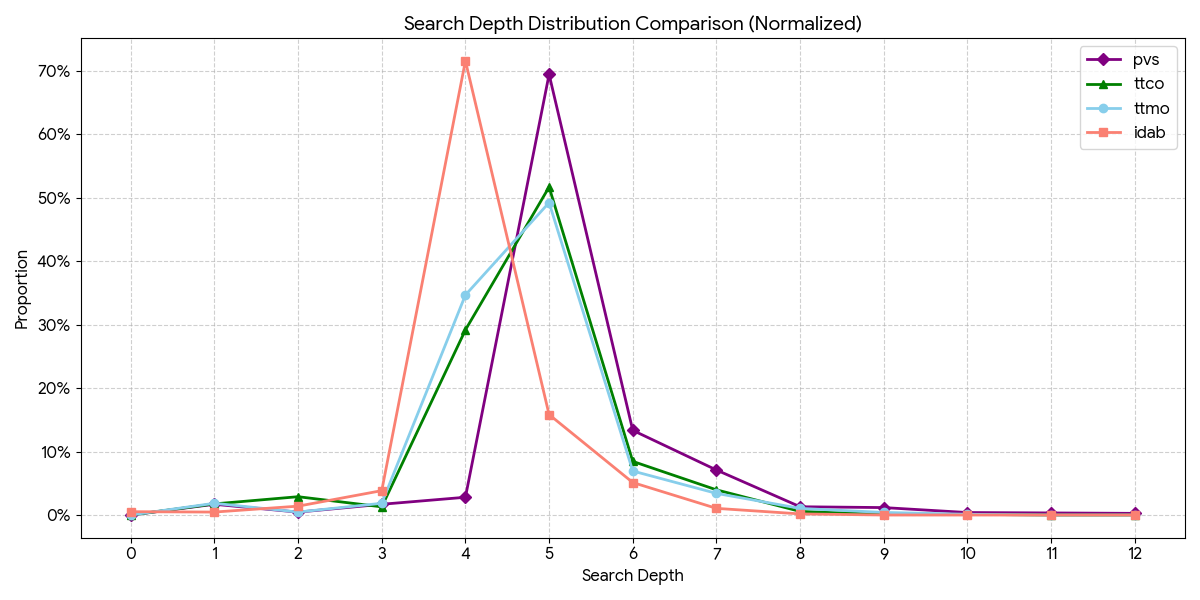
또한, PVS를 사용하는 경우 탐색 깊이가 더 증가하는 걸 알 수 있습니다.

7. Summary

이번 글에서는 Minimax 에이전트의 탐색 속도와 효율을 개선하기 위한 다양한 기법들을 단계적으로 적용하고 검증해보았습니다.

Alpha-Beta Pruning: 탐색할 필요가 없는 가지를 쳐내어 Baseline 대비 $5\sim10$배 빠른 연산 속도를 얻습니다.
Iterative Deepening: 고정 깊이 탐색을 시간 제한 내에서 가능한 가장 깊은 수를 찾도록 변형해 제한 시간에 맞는 깊이를 선택합니다.
Transposition Table: 해시 테이블을 도입하여 중복 연산을 방지하고, Move Ordering을 통해 좋은 수를 먼저 탐색하며 Pruning 효율을 높입니다.
Principal Variation Search: Move Ordering이 잘 되었다는 가정하에 첫 번째 수(PV)를 제외한 나머지 수들에 Null Window Search를 적용하여 추가적인 성능 향상을 얻습니다.

실험 결과, Minimax 에이전트를 Alpha-Beta Pruning을 기본으로 Iterative Deepening, Transposition Table을 이용한 Move Ordering, PVS와 같은 최적화를 적용함에 따라 에이전트의 성능이 개선되는 걸 확인할 수 있었습니다. 이는 여러 탐색 최적화가 성능 개선에 큰 영향을 미친다는 걸 의미합니다.

다음 글에서는 탐색 알고리즘만큼이나 중요한 Evaluation Function을 정교하게 설계하는 방법이나, 신경망을 접목한 NNUE, 그리고 Minimax와는 다른 탐색 방식인 MCTS 등에 대해 다뤄보겠습니다.