Tensor Network
텐서 네트워크(Tensor Network Diagram)는 양자 컴퓨팅, 인공지능에 이르기까지 다양한 분야에서 활용되는 강력한 수학적 도구입니다. 복잡해 보이는 텐서 연산을 쉽게 하기 위해서는 다양한 트릭들이 필요한데, 텐서 네트워크는 텐서간의 연산을 그래프로 표현해서 복잡한 연산을 간단하고 직관적으로 다룰 수 있게 해줍니다. 이번 포스트에서는 텐서 네트워크 중에서도 양자 컴퓨팅에 자주 쓰이는 부분들을 소개하고자 합니다. 내용은 참고문헌 [1]을 주로 참고하였습니다.
Quick Review: Bra-Ket Notation
우선 기본적인 bra-ket 표기법은 간략하게만 복습하고 넘어가겠습니다. bra-ket 표기법은 Paul Dira이 1939년에 제안한 표기법으로, 양자 상태를 표현하고 연산하는데 널리 사용됩니다. ket $\vert \psi \rangle$는 열벡터 입니다. 그리고 bra $\langle \psi \vert$는 $\vert \psi \rangle$ 의 켤레전치 입니다. 따라서 행벡터입니다. 열벡터 $v, w$ 사이 dot product는 $v^\dagger w$로 계산되지만, 이것과 동일한 연산을 bra-ket 표기법으로 표현하면 $\langle v \vert w \rangle$가 됩니다. 괄호가 닫힘으로써 저 결과가 스칼라임을 직관적으로 알 수 있게 해줍니다. 중간에 행렬을 넣었다면 $\langle v \vert A \vert w \rangle$ 와 같이 표현할 수 있습니다. 이 역시 괄호로 닫혀 있기 때문에 스칼라 결과임을 알 수 있습니다. $A\vert w \rangle$ 는 행렬 $A$가 벡터 $\vert w \rangle$에 작용한 결과 벡터이며, 오른쪽만 괄호가 닫혀 있으므로 열 벡터임을 알 수 있습니다.
간단한 응용 예시로, 행렬 A에 대해 $(A)_{ij} = \langle i \vert A \vert j \rangle$ 로 표현할 수 있습니다. 여기서 $\vert i \rangle$ 는 표준 기저 벡터입니다.
Introduction to Tensor Network Diagram
텐서 네트워크 다이어그램은 텐서와 그 연산을 시각적으로 표현하는 방법입니다. 텐서 네트워크 다이어그램에서는 텐서를 도형으로 나타내고, 텐서의 차원은 도형에서 뻗어나오는 선으로 표현됩니다. 이 다이어그램을 사용하면 복잡한 텐서 연산을 직관적으로 이해하고 계산할 수 있습니다.
값의 표기법 소개
ket $\vert \psi \rangle$ 는 tensor network diagram 에서는 아래 그림과 같이 표현됩니다.
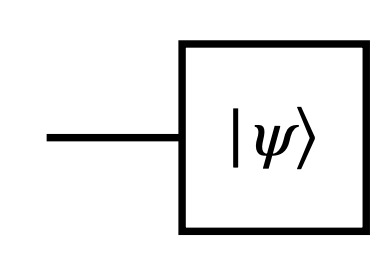
Tensor network diagram에서 텐서는 도형으로 표현되고, 텐서의 각 차원은 도형에서 뻗어나오는 선으로 표현됩니다. 위 그림에서는 ket $\vert \psi \rangle$가 1차원 텐서이므로 왼쪽에서 하나의 선이 뻗어나오고 있습니다. 이제 bra를 살펴봅시다.
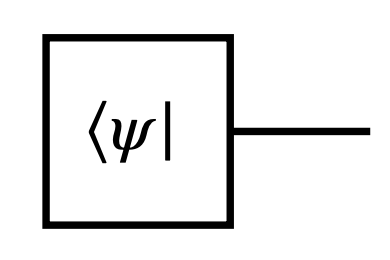
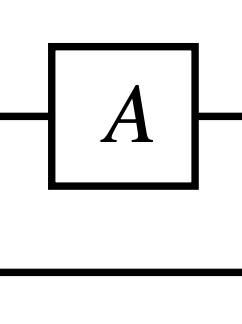
bra $\langle \psi \vert$는 ket의 켤레전치이므로, 텐서 네트워크 다이어그램에서는 ket와 동일한 도형이지만 선이 오른쪽에서 뻗어나오는 것으로 표현됩니다. 이제 행렬을 살펴봅시다. 여기서 다루는 모든 행렬은 $A \in L(\mathbb{C}^d)$ 의 복소수 행렬입니다.

Idneity matrix는 아무 동작도 없으므로 사각형 도형은 생략하고 양옆의 선만 이어서 표시합니다. 즉, 직선입니다.
(관찰 1) 오른쪽에 선이 뻗어나오는 것의 의미는 행렬이 벡터를 출력한다는 의미이고, 왼쪽에 선이 뻗어나오는 것의 의미는 행렬이 벡터를 입력받는다는 의미입니다.
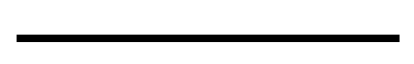
이제 행렬의 Transpose를 어떻게 표시하는지 보면 tensor network의 철학을 이해하는데 도움이 될 거라 생각합니다.
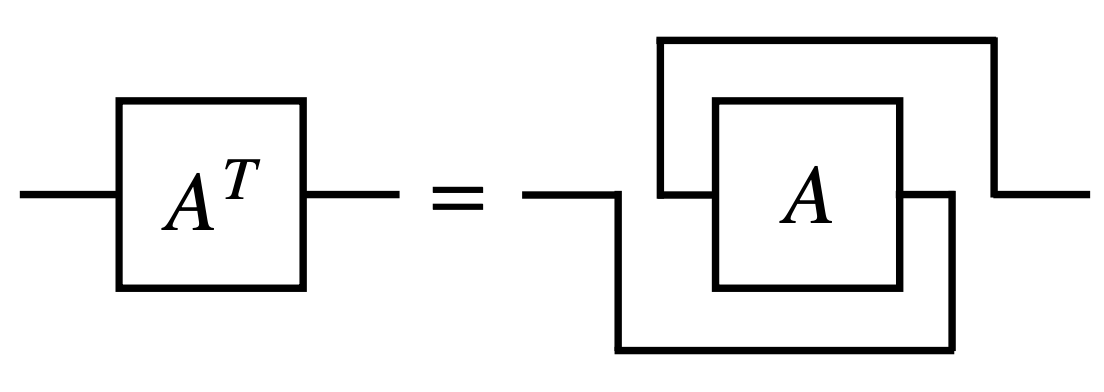
의미 없는 복잡한 표현처럼 보이지만, 사실은 간단한 철학이 숨어 있습니다. 행렬 $A$의 transpose $A^T$는 행과 열이 바뀐 행렬입니다. tensor network diagram에서 행렬 $A$는 왼쪽에서 선이 들어오고 오른쪽에서 선이 나가는 도형으로 표현됩니다. 따라서 transpose $A^T$는 선의 방향이 바뀌어 오른쪽에서 선이 들어오고 왼쪽에서 선이 나가는 도형으로 표현됩니다. 사각형을 180도 뒤집어서 회전시키면 되겠지만, tensor network diagram에서는 도형을 놔둔 채로 선을 뒤집어서 내보내는 방식으로 표현합니다.
연산의 표기법 소개
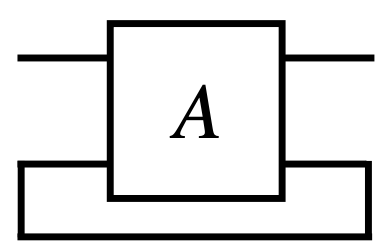
이제 Tensor network diagram에서 연산을 어떻게 표기하는지 살펴봅시다. 먼저, 가장 간단한 연산인 trace 부터 살펴보겠습니다.

Trace 연산은 행렬의 대각 원소들의 합을 구하는 연산입니다. tensor network diagram에서 trace 연산은 행렬의 출력 선과 입력 선을 연결하여 닫힌 루프를 형성함으로써 표현됩니다. 연결성이 중요하기 때문에 위로 연결하거나 아래로 연결하는 것은 동일하게 취급됩니다.
(관찰 2) 닫힌 루프는 스칼라입니다. 출력을 내보내지도 못하고 입력도 받지 못하기 때문입니다.
이제 행렬 곱을 tensor network에서 어떻게 표기하는지 살펴봅시다.
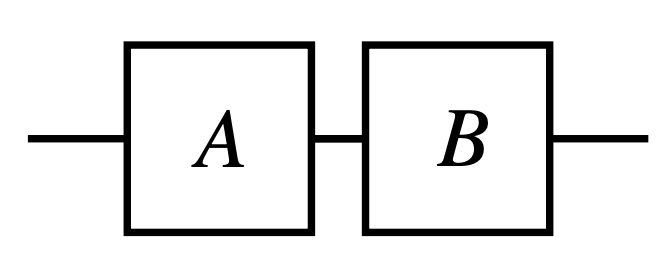
이제 $A \otimes B \in L(\mathbb{C}^d \otimes \mathbb{C}^d)$ 의 tensor network diagram 표기법을 살펴봅시다.
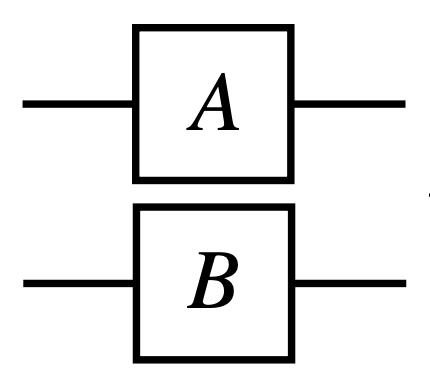
tensor product $A \otimes B$ 은 두 subsystem 에 각각 적용되는 연산입니다. 따라서 입력 선이 두 개, 출력 선이 두 개인 도형으로 표현됩니다. 이 직관을 사용해서 $A \in L(\mathbb{C}^d \otimes \mathbb{C}^d)$ 을 표현해 봅시다. 입력이 두개, 출력이 두 개인 한 개의 도형일 것입니다.
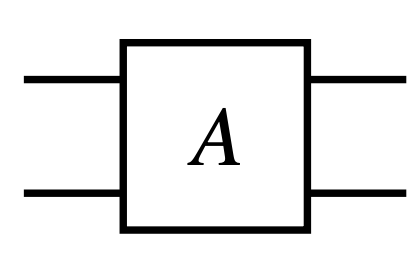
(관찰 3) 여러 개의 subsystem에 작용한다면 여러 개의 입력 선을 가집니다. 출력이 여러 개의 subsystem을 가진다면 여러 개의 출력 선을 가집니다.
조금 응용해 봅시다. 부분 trace 연산은 특정 system을 trace취해 버려서 상수를 뽑아내어 차원을 낮추는 연산입니다. 예를 들어 봅시다. $A \in L(\mathbb{C}^d \otimes \mathbb{C}^k)$ 에 대해서 아래 두 개의 식이 성립합니다. Tr 밑에 적는 값은 남길 subsystem 이 아니라 날려버릴 subsystem의 번호라는 점을 주의합시다.
- $\mathrm{Tr}_1(A) \in L(\mathbb{C}^k)$ (첫 번째 subsystem을 trace out)
- $\mathrm{Tr}_2(A) \in L(\mathbb{C}^d)$ (두 번째 subsystem을 trace out)
이제 $Tr_2(A)$ 의 tensor network diagram 는 아래와 같이 표현됩니다.
$Tr_2$ 이므로 두 번째 subsystem의 입력 선과 출력 선이 연결되어 닫힌 루프를 형성하고 있습니다. 그림 3-1에서 살펴본 trace 연산의 표기법과 동일합니다. 만약 $Tr_1(A)$ 였다면 첫 번째 subsystem의 입력 선과 출력 선이 연결되었을 것입니다.
Vectorization 관련 표기법 소개
먼저 Vectorization 이 무엇인지 간단하게 살펴보겠습니다. Vectorization 은 행렬을 벡터로 바꾸는 연산입니다. 즉, Flatten 입니다. 수식으로 먼저 살펴보면 헷갈릴 수도 있으니, 간단한 예시를 들어 보겠습니다.
행렬 $A = \begin{pmatrix} a & b \ c & d \end{pmatrix} \in L(\mathbb{C}^2)$ 에 대해서 vectorization 연산을 적용하면 $\vert A \rangle\rangle = \begin{pmatrix} a \ c \ b \ d \end{pmatrix} \in \mathbb{C}^4$ 가 됩니다. 즉, 행렬의 열(column)들을 차례대로 이어붙여서 하나의 열벡터로 만드는 연산입니다.
3*3 행렬도 살펴봅시다. 행렬 $B = \begin{pmatrix} a & b & c \ d & e & f \ g & h & i \end{pmatrix} \in L(\mathbb{C}^3)$ 에 대해서 vectorization 연산을 적용하면 $\vert B \rangle\rangle = \begin{pmatrix} a \ d \ g \ b \ e \ h \ c \ f \ i \end{pmatrix} \in \mathbb{C}^9$ 가 됩니다.
(관찰 4) Vectorization 연산은 행렬의 열(column)들을 차례대로 이어붙여서 하나의 열벡터로 만드는 연산입니다. $M_{n,n}(\mathbb{C})$ 에 속하는 행렬은 $n^2$ 차원의 벡터로 바뀝니다.
이제, vectorization이 무엇인지 감을 잡았으니, 수식으로 표현해 봅시다. $\vert \Omega \rangle = \sum_{i=1}^{d} \vert i \rangle \otimes \vert i \rangle$ 라고 정의하면, $A \in L(\mathbb{C}^d)$ 의 vecterization 결과는
\[\vert A \rangle\rangle = A \otimes I \vert \Omega \rangle \in \mathbb{C}^d \otimes \mathbb{C}^d\]위 식의 증명:
\[A \otimes I \vert \Omega \rangle = A \otimes I \sum_{i=1}^{d} \vert i \rangle \otimes \vert i \rangle = \sum_{i=1}^{d} A\vert i \rangle \otimes I \vert i \rangle = \sum_{i=1}^{d} A\vert i \rangle \otimes \vert i \rangle\] \[= \sum_{i=1}^{d} (\sum_{j=1}^{d} A_{ji} \vert j \rangle) \otimes \vert i \rangle = \sum_{i=1}^{d} \sum_{j=1}^{d} A_{ji} (\vert j \rangle \otimes \vert i \rangle) = \vert A \rangle\rangle\](관찰 5) $\vert \Omega \rangle = \sum_{i=1}^{d} \vert i \rangle \otimes \vert i \rangle$ 는 사실 항등행렬을 vectorization 한 것입니다. 즉, $\vert \Omega \rangle = \vert I \rangle\rangle$ 입니다. 항등행렬을 이어서 붙여보면 자명함을 쉽게 알 수 있습니다.
드디어 tensor network diagram에서 vectorization을 어떻게 표현하는지 살펴볼 차례입니다. $\vert \Omega \rangle = \vert I \rangle\rangle$ 의 tensor network diagram 표기법은 아래와 같습니다.
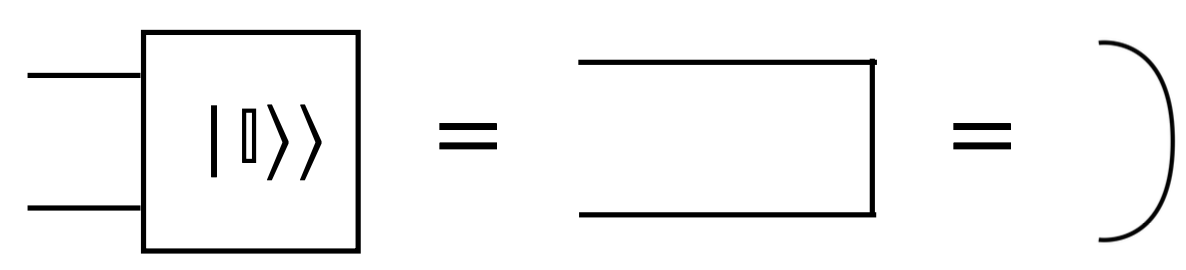
2개의 subsystem을 가지는 열벡터(ket)이므로 왼쪽에 두개의 선이 뻗어나오는 도형으로 표현됩니다. 이제 여기서부터 tensor network diagram의 진가가 나오기 시작합니다. 한번 $A \in L(\mathbb{C}^d)$ 의 vectorization $\vert A \rangle\rangle = A \otimes I \vert \Omega \rangle$ 의 tensor network diagram 표기법을 그려봅시다.
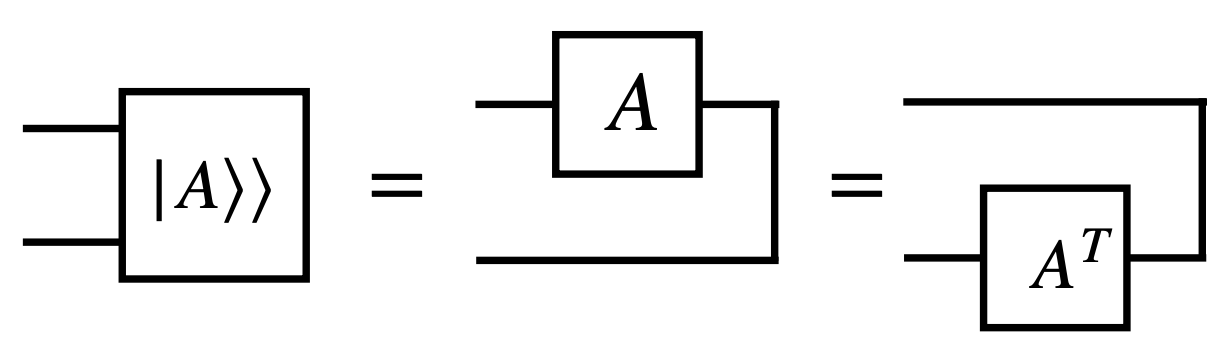
복잡해 보여도, $A^T$ 의 성질을 이용해서 다시 그려보면 직관적으로 이해할 수 있습니다.
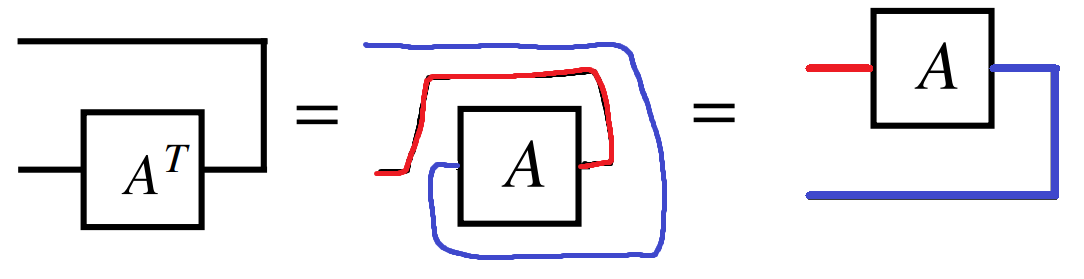
(관찰 6) tensor network diagram에서 행렬을 밀어서 밑으로 보내면 전치 행렬이 된다. 다시 밑에서 위로 올리면 원래 행렬이 된다.
이제 수식적으로 이해해 봅시다. 분해해 보면 간단합니다. Vectorization 연산은 $A \otimes I$ 에 $\vert \Omega \rangle$ 를 곱하는 연산이므로,
여기에다가 $\vert \Omega \rangle$ (그림 5)를 곱한것입니다. 행렬 곱은 단순히 횡으로 연결하는 것이므로 (그림 3-2 참고) 그림 5의 결과를 얻을 수 있습니다.
그 뒤의 관계가 성립하는 이유는 $\vert A \rangle\rangle = A \otimes I \vert \Omega \rangle = I \otimes A^T \vert \Omega \rangle$ 관계가 성립하기 때문입니다. 이는 매우 유명한 trick 이며, 증명 과정은 다음과 같습니다.
\(I \otimes A^T \vert \Omega \rangle = I \otimes A^T \sum_{i=1}^{d} \vert i \rangle \otimes \vert i \rangle = \sum_{i=1}^{d} I \vert i \rangle \otimes A^T \vert i \rangle\) \(= \sum_{i=1}^{d} \vert i \rangle \otimes A^T \vert i \rangle = \sum_{i=1}^{d} \vert i \rangle \otimes (\sum_{j=1}^{d} A_{ji} \vert j \rangle)\) \(= \sum_{i=1}^{d} \sum_{j=1}^{d} A_{ji} (\vert i \rangle \otimes \vert j \rangle) = \vert A \rangle\rangle\)
하지만 tensor network diagram에서는 이 관계가 직관적으로 이해됩니다. 그림 5-1의 가운데 figure을 봅시다. 행렬 A를 오른쪽으로 밀어서 넘겨주면 자연스럽게 뒤집히게 되고, 선의 방향이 바뀌면서 transpose가 되는 것입니다. 즉, tensor network diagram에서는 vectorization의 두 표현이 동일하게 보이기 때문에 자연스럽게 성립하는 관계가 되는 것입니다. 이 옮김을 자연스럽게 해보면 ABC rule 을 얻습니다.

만약 행렬 A가 $A \in L(\mathbb{C}^d) \otimes L(\mathbb{C}^{d’})$ 에 속하는 행렬이라면, vectorization 결과는 $\vert A \rangle\rangle \in \mathbb{C}^d \otimes \mathbb{C}^{d’} \otimes \mathbb{C}^d \otimes \mathbb{C}^{d’}$ 에 속하는 벡터가 됩니다. tensor network diagram 표기법은 다음과 같습니다.
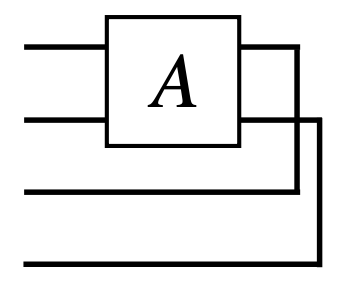
Row Vectorization
Row vectorization 도 존재합니다. Row vectorization 은 행렬의 행(row)들을 차례대로 이어붙여서 하나의 열벡터로 만드는 연산입니다. 수식으로 표현하면 다음과 같습니다.
\[\langle \langle A \vert = \langle \Omega \vert A \otimes I = \sum_{i=1}^{d} \langle i \vert \otimes \langle i \vert A\]Row vectorization 의 tensor network diagram 표기법은 다음과 같습니다.
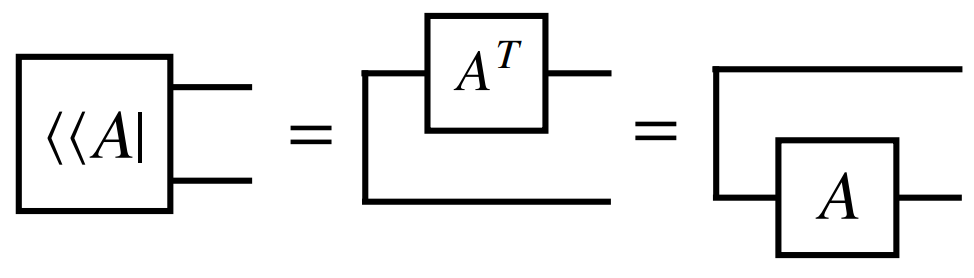
행렬 $A$와 $B$의 내적값은 보통 $tr(A^T B)$ 로 정의하는데, 이 값은 벡터화한 값들 사이의 내적과 동일합니다. 따라서 $\langle \langle A\vert B\rangle \rangle = \text{Tr}(A^T B)$ 가 성립하고, tensor diagram으로 표현한다면 아래와 같이 표현됩니다.
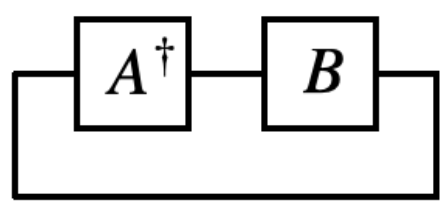
Tensor network의 표기법에 뭔가 일관성이 보이기 시작합니다.
Swap Operator
두 subsystem 의 상태를 맞바꾸는 연산을 swap operator 라고 합니다. 수식으로 표현하면 다음과 같습니다.
\[\mathbb{F} \vert \psi \rangle \otimes \vert \phi \rangle = \vert \phi \rangle \otimes \vert \psi \rangle\]이를 tensor network diagram 으로 표현하면 다음과 같습니다.

마지막으로 swap trick $\text{Tr}_2(AB) = \text{Tr}_2((A \otimes B)\mathbb{F})$ 를 tensor network diagram으로 표현해 봅시다.

이걸 조금만 응용하면, 동일한 방식으로 $\text{Tr}_2(\mathbb{F}(A \otimes B)) = \text{Tr}BA)$ 도 쉽게 보일 수 있습니다.
Example problem
- $A, B \in \mathbb{C}^{d}$ 일 때, $\text{Tr}(AB) = \text{Tr}(BA)$ 임을 tensor network diagram을 사용해서 이해하시오.
정답 보기
풀이: B행렬을 오른쪽으로 밀어서 밑으로 내리면 B^T 가 됩니다. 이번엔 왼쪽으로 밀어서 다시 올린다면 A왼쪽에 B가 붙게 됩니다.- $A, B, X \in \mathbb{C}^{d}$ 일 때, $\vert AXB^T \rangle\rangle = A \otimes B \vert X \rangle\rangle$ 임을 tensor network diagram을 사용해서 이해하시오.
정답 보기
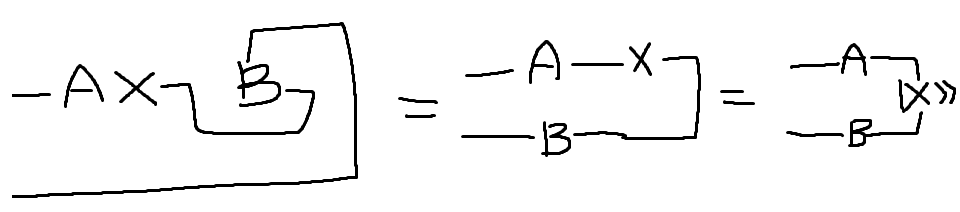
참고문헌
[1] Mele, Antonio Anna. “Introduction to Haar measure tools in quantum information: A beginner’s tutorial.” Quantum 8 (2024): 1340.