K-Center Problem in Tree
1. Introduction
k-center problem은 그래프에서 $k$개의 센터를 선택하여 모든 정점으로부터 가장 가까운 센터까지의 거리의 최댓값을 최소화하는 최적화 문제입니다. 이는 도시 내에 소방서나 응급 의료 센터와 같은 필수 시설을 배치할 때, 가장 가까운 시설까지의 거리가 일정 수준을 넘지 않도록 해야 하는 상황에서 주로 사용됩니다.
일반 그래프에서의 k-center problem은 NP-hard로 알려져 있으며, $P \neq NP$ 가정 하에 2-approximation보다 나은 근사 알고리즘 또한 NP-hard임이 증명되어 있습니다. 때문에 일반 그래프에서는 근사 알고리즘을 이용한 접근이나, 그래프의 특수한 구조를 이용하는 접근이 주로 시도됩니다.
그래프가 트리라면 두 정점 사이의 경로가 유일하므로, k-center problem을 전역적인 최적화 문제를 국소적인 최적화 문제로 환원할 수 있습니다. 이때 국소적인 최적화 문제는 greedy하게 해결할 수 있어 트리에서의 k-center problem은 다항 시간 내에 정확한 해를 구할 수 있습니다.
트리의 k-center problem은 문제 상황에 따라 여러 변형을 가집니다. 대표적으로 간선 가중치의 존재 여부나 센터를 정점에만 둘 수 있는지 혹은 간선의 중간에도 둘 수 있는지에 따른 변형이 존재합니다. 이 글에서는 기본적인 트리의 k-center problem을 시작으로, 이러한 변형 문제를 해결하는 방법을 단계적으로 알아보겠습니다.
2. K-Center Problem In General Graph
그래프의 k-center problem은 일반 그래프 $G = (V, E)$에서 $k$개의 센터를 선택하여, 모든 정점으로부터 가장 가까운 센터까지의 거리의 최댓값을 최소화하는 문제입니다.
\[\min_{S \subseteq V, \vert S\vert = k} \max_{v \in V} \min_{s \in S} \text{dist}(v, s)\]그래프의 k-center problem이 어려운 이유는 그래프에서 한 정점의 선택이 다른 모든 정점에 미치는 영향이 서로 복잡하게 얽혀있기 때문입니다. 한 정점에서 다른 정점으로 이동하는 경로는 여러 개가 존재하기에, 일반 그래프에서는 거리의 전파가 국소적인 구조로 분해되지 않습니다.
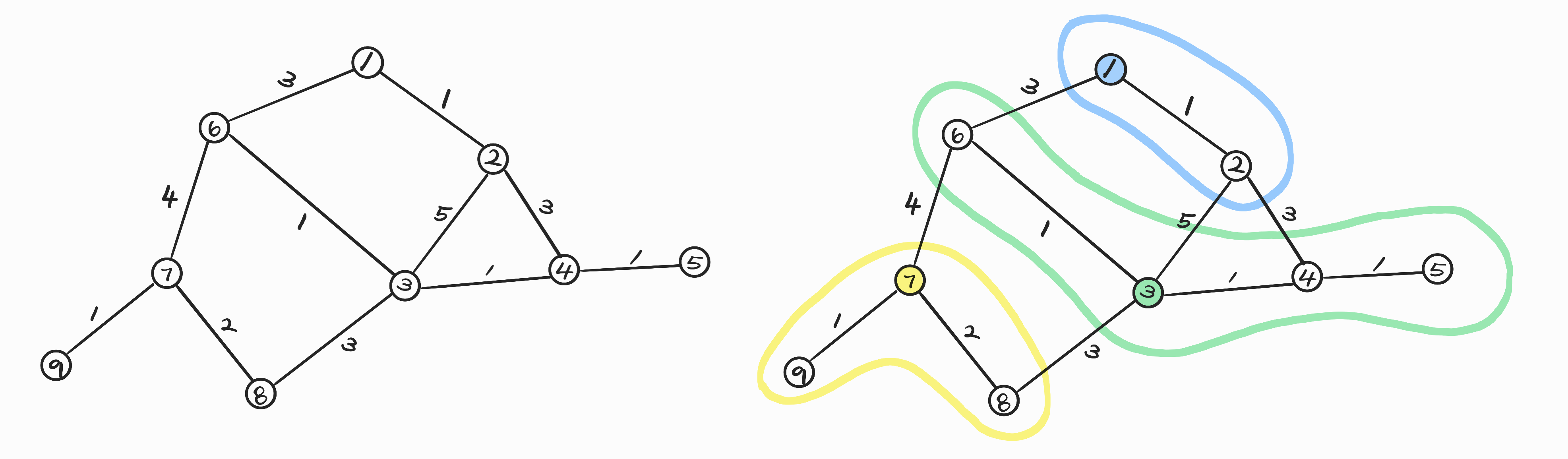
예를 들면, 위와 같은 그래프에서 $k = 3$인 k-center problem의 최적해는 $2$입니다. 가능한 $\vert S\vert = 3$이고, $\max_{v\in V}\min_{s\in S}\text{dist}(v, s) = 2$인 집합 $S$는 ${ 1, 3, 7 }, { 1, 4, 7 }, { 2, 3, 7 }, { 2, 4, 7 }$이 있습니다.
일반 그래프에서 k-center problem은 다항 시간 풀이가 알려져 있지 않기에 그 자체로는 자주 출제되지는 않으며, $k = 1$이거나 $\text{dist}$ 함수가 metric이라는 조건을 추가한 변형 문제가 종종 출제됩니다.
3. K-Center Problem In Tree
k-center problem에서 그래프 $G$가 트리라는 조건이 있다면 문제를 효율적으로 해결할 수 있습니다.
먼저 거리 제한 $x$가 주어질 때 필요한 최소 센터의 개수를 반환하는 함수 $f(x)$를 다음과 같이 정의합시다.
\[f(x) := \min \vert S\vert \text{ s.t.} \max_{v\in V}\min_{s\in S}\text{dist}(v, s) \le x\]집합 $S$가 $\max_{v\in V}\min_{s\in S}\text{dist}(v, s) \le x$를 만족한다면 $\max_{v\in V}\min_{s\in S}\text{dist}(v, s) \le x + 1$ 또한 만족합니다. 따라서 정의에 의해 모든 $x$에 대해 $f(x) \ge f(x + 1)$이 성립합니다.
이러한 단조성을 이용하면 $f(x) \le k$를 만족하는 $x$의 최솟값을 이분 탐색binary search으로 구하며 k-center problem의 최적해를 구할 수 있습니다. 일반적인 그래프에서는 $f(x)$를 계산하는 결정 문제 자체가 NP-hard에 해당하며 매우 어렵지만, 트리에서는 사이클이 없는 계층적 구조 덕분에 $f(x)$를 다항 시간 내에 빠르게 계산할 수 있습니다.
3.1 Unweighted Tree with Discrete Centers
모든 간선의 가중치가 $1$이면서 $S \subseteq V$인 경우에는 $f(x)$를 $\mathcal{O}(N)$에 구할 수 있습니다.
$1$번 정점을 루트로 두고, $i$번 정점을 루트로 하는 subtree를 $T_i$로 정의합시다. $T_i$의 모든 정점 $u$에 대해 $\text{dist}(i, u) < x$라면 $i$번 정점을 하얀색 정점, 그렇지 않다면 검은색 정점이라 하겠습니다.
어떤 정점 $i$가 검은색 정점이면서 $T_i$에 자기 자신을 제외한 다른 검은색 정점이 없다면 $i$를 포함하는 최적 집합 $S$가 존재합니다. 증명은 교환 논증exchange argument를 이용합니다. $i$를 포함하지 않는 최적 집합 $S^\ast$가 있다고 가정합시다. 그러면 어떤 정점 $u \in T_i$가 존재해서 $u \in S^\ast$여야 합니다. 이때 $S^\ast$에서 $u$를 제거하고 $i$를 추가해 만든 집합 $S$ 또한 제한 조건을 만족하니 교환 논증이 성립합니다.
비슷하게, $T_i$의 정점 중 가장 가까운 센터까지의 거리가 $x$ 초과인 모든 정점 $u$에 대해 $\text{dist}(i, u) < x$라면 $i$번 정점을 하얀색 정점, 그렇지 않다면 검은색 정점이라 하면 subtree 내에서 센터를 선택한 경우에도 같은 논리를 적용할 수 있습니다.
따라서 dfs 과정에서 $T_i$에서 1)가장 가까운 센터까지의 거리가 $x$ 초과인 정점 $u$에 대한 $\max(\text{dist}(i, u))$값과 2)센터로 정한 정점 $v$에 대한 $\min(\text{dist}(i, v))$값을 관리하면서 greedy하게 $i$번 정점이 검은색 정점인지 여부를 판별하며 $f(x)$를 선형 시간에 계산할 수 있습니다. 이를 이용하면 이분 탐색으로 $\mathcal{O}(N\log N)$에 k-center problem을 해결할 수 있습니다.
3.2 Weighted Tree with Discrete Centers
트리의 간선에 양의 가중치가 있는 경우에도 같은 논리를 적용할 수 있습니다.
주의할 점은 간선의 가중치가 모두 $1$이라면 처음으로 가장 가까운 센터까지의 거리가 $x$ 초과이면서 $\text{dist}(i, u) \ge x$인 정점 $u$가 등장할 때에만 $i$번 정점을 센터로 지정하는 방법이 가능했지만, 간선의 가중치가 커질 수 있는 경우에는 $i$번 정점을 센터로 지정하더라도 $\text{dist}(i, u) > x$일 수 있다는 점입니다. 때문에 이러한 경우에는 $i$번 정점이 아니라 $u$를 포함하는 $i$번 정점의 자식 정점 $c$를 센터로 지정해야 합니다.
정리하면, Unweighted Tree에서와 마찬가지로 dfs 과정에서 현재 정점 $i$를 선택하지 않으면 가장 가까운 센터까지의 거리가 $x$ 초과가 되는 정점 $u$가 생길 때, 자식 정점 $c$를 센터로 지정하는 greedy 방법으로 $f(x)$를 $\mathcal{O}(N)$에 구할 수 있습니다. 이를 이용하면 이분 탐색으로 $\mathcal{O}(N\log(\max(w_i)))$에 k-center problem을 해결할 수 있습니다.
3.3 Weighted Tree with Continuous Centers
트리의 정점 뿐만 아니라 간선 위의 임의의 지점에서 센터를 고를 수 있을 때 k-center problem을 해결하는 방법을 생각해봅시다.
이 경우 또한 마찬가지로 최대한 깊이가 얕은 지점을 센터로 정하면서 1)가장 먼 cover되지 않은 지점까지의 거리와 2)가장 가까운 센터까지의 거리를 관리하는 dfs로 greedy하게 $f(x)$를 $\mathcal{O}(N)$에 계산할 수 있습니다.
4. Practice Problems
지금까지의 논의를 이용하면 다음의 문제를 해결할 수 있습니다.
4.1 BOJ 23572 - Logistical Warehouse 2
제한: $1 \le K \le N \le 10^5$
$N$개의 정점으로 이루어진 트리 $T = (V, E)$가 주어집니다. 트리의 두 정점 $a, b$에 대해 $\text{dist}(a, b)$를 $a$와 $b$를 잇는 유일한 단순 경로 상의 간선의 개수로 정의합니다. 다음 조건을 만족하는 $S \subseteq V$에 대해 $\vert S\vert$의 최솟값을 구해야 합니다.
\[\forall v \in V, \; \min_{s \in S}{\text{dist}(v, s)} \le K\]위에서 정의한 $f(x)$를 이용하면, 문제에서 요구하는 값은 $f(K)$임을 알 수 있습니다.
따라서 기존 논의를 이용하면 greedy하게 $\mathcal{O}(N)$에 문제를 해결할 수 있습니다.
다음은 문제를 해결하는 예시 코드입니다.
#include <bits/stdc++.h>
using namespace std;
constexpr int inf = 1 << 30;
auto sol = [](int n, int k, auto adj) {
int ret = 0;
auto rec = [&](const auto& self, int cur, int prv) -> pair<int, int> {
int mn = inf, mx = 0;
for (int nxt : adj[cur]) {
if (nxt == prv) continue;
auto [a, b] = self(self, nxt, cur);
if (a != inf) mn = min(mn, a + 1);
if (b != -inf) mx = max(mx, b + 1);
}
if (mn != inf && mn + mx <= k) mx = -inf;
if (mx == k) ret++, mn = 0, mx = -inf;
return pair(mn, mx);
};
if (rec(rec, 1, 0).second != -inf) ret++;
return ret;
};
int main() {
cin.tie(0)->sync_with_stdio(0);
int n, k; cin >> n >> k;
vector adj(n + 1, vector(0, 0));
for (int i = 1; i < n; i++) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
cout << sol(n, k, adj) << '\n';
}
재귀 함수에서 반환하는 값은 1)가장 가까운 센터까지의 거리가 $x$ 초과인 정점 $u$에 대한 $\max(\text{dist}(i, u))$값과 2)센터로 정한 정점 $v$에 대한 $\min(\text{dist}(i, v))$값입니다.
4.2 BOJ 28219 - 주유소
제한: $1 \le K < N \le 2 \cdot 10^5$
$N$개의 정점으로 이루어진 트리 $T = (V, E)$가 주어집니다. 트리의 두 정점 $a, b$에 대해 $\text{dist}(a, b)$를 $a$와 $b$를 잇는 유일한 단순 경로 상의 간선의 개수로 정의합니다. 또한 $a$와 $b$를 잇는 유일한 단순 경로를 $P(a, b)$라 하겠습니다. 다음 조건을 만족하는 $S \subseteq V$에 대해 $\vert S\vert$의 최솟값을 구해야 합니다.
\[\forall a, b \in V \land \text{dist}(a, b) = K, \; \exists u \in P(a, b), u \in S\]이는 어떤 정점 $u$를 골라 트리에서 제거하는 연산을 최소한으로 이용해 각 component의 지름을 $k$ 미만으로 만드는 문제와 동치입니다.
트리의 k-center problem를 해결할 때와 비슷하게, subtree의 지름이 $k$ 이상인 정점을 검은색 정점, 나머지 정점을 하얀색 정점이라 하겠습니다. 이러면 dfs 과정에서 검은색 정점이 나올 때마다 해당 정점을 $S$에 포함시키는 greedy 전략이 성립하고, 따라서 $\mathcal{O}(N)$에 문제를 해결할 수 있습니다.
다음은 문제를 해결하는 예시 코드입니다.
#include <bits/stdc++.h>
using namespace std;
auto sol = [](int n, int k, auto adj) {
int ret = 0;
auto rec = [&](const auto& self, int cur, int prv) -> int {
int mx = 1, flag = 0;
for (int nxt : adj[cur]) {
if (nxt == prv) continue;
int res = self(self, nxt, cur);
if (mx + res > k) flag = 1;
mx = max(mx, res + 1);
}
if (flag) ret++, mx = 0;
return mx;
};
rec(rec, 1, 0);
return ret;
};
int main() {
cin.tie(0)->sync_with_stdio(0);
int n, k; cin >> n >> k;
vector adj(n + 1, vector(0, 0));
for (int i = 1; i < n; i++) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
cout << sol(n, k, adj) << '\n';
}
4.3 BOJ 8213 - Dynamite
제한: $1 \le K \le N \le 3 \cdot 10^5$
$N$개의 정점으로 이루어진 트리 $T = (V, E)$와 다이너마이트가 설치된 정점의 집합 $D \subseteq V$가 주어집니다. 트리의 두 정점 $a, b$에 대해 $\text{dist}(a, b)$를 $a$와 $b$를 잇는 유일한 단순 경로 상의 간선의 개수로 정의합니다. 다음 조건을 만족하는 $S \subseteq V$이고 $\vert S\vert \le K$인 집합 $S$에 대해 $\max_{v \in D} \min_{s \in S} \text{dist}(v, s)$의 최솟값을 구해야 합니다.
$f(x)$를 $\max_{v \in D} \min_{s \in S} \text{dist}(v, s) \le x$를 만족하는 $S$에 대한 $\vert S\vert$의 최솟값으로 정의하면, $f(x) \le K$를 만족하는 $x$의 최솟값을 구하면 됩니다.
이렇게 정의한 $f(x)$는 기존 문제와 마찬가지로 정점을 선택해야만 하는 경우에만 선택하는 greedy를 이용해 $\mathcal{O}(N)$에 구할 수 있습니다.
다음은 문제를 해결하는 예시 코드입니다.
#include <bits/stdc++.h>
using namespace std;
constexpr int inf = 1 << 30;
auto sol = [](int n, int k, auto v, auto adj) {
auto check = [&](int x) {
int cnt = 0;
auto rec = [&](const auto& self, int cur, int prv) -> pair<int, int> {
int mn = inf, mx = v[cur] ? 0 : -inf;
for (int nxt : adj[cur]) {
if (nxt == prv) continue;
auto [a, b] = self(self, nxt, cur);
if (a != inf) mn = min(mn, a + 1);
if (b != -inf) mx = max(mx, b + 1);
}
if (mn != inf && mx != -inf && mn + mx <= x) mx = -inf;
if (mx == x) cnt++, mn = 0, mx = -inf;
return pair(mn, mx);
};
if (rec(rec, 1, 0).second != -inf) cnt++;
return cnt <= k;
};
int lo = -1, hi = n;
while (lo + 1 < hi) {
int mid = lo + hi >> 1;
if (!check(mid)) lo = mid;
else hi = mid;
}
return hi;
};
int main() {
cin.tie(0)->sync_with_stdio(0);
int n, k; cin >> n >> k;
vector v(n + 1, 0);
vector adj(n + 1, vector(0, 0));
for (int i = 1; i <= n; i++) cin >> v[i];
for (int i = 1; i < n; i++) {
int a, b; cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
cout << sol(n, k, v, adj) << '\n';
}
4.4 BOJ 24472 - Parkovi
제한: $1 \le K \le N \le 2 \cdot 10^5$
$N$개의 정점으로 이루어진 트리 $T = (V, E)$가 주어집니다. 트리의 각 간선에는 $[1, 10^9]$ 범위의 정수 가중치가 부여되어 있습니다. 트리의 두 정점 $a, b$에 대해 $\text{dist}(a, b)$를 $a$와 $b$를 잇는 유일한 단순 경로 상의 간선의 가중치 합으로 정의합니다. 다음 조건을 만족하는 $S \subseteq V$이고 $\vert S\vert = K$인 집합 $S$에 대해 $\max_{v \in V} \min_{s \in S} \text{dist}(v, s)$의 최솟값을 구해야 합니다.
본문에서 다룬 weighted tree with discrete centers case에 해당하는 k-center problem입니다. 설명한 것과 같이 자식 노드를 선택해야 할 수도 있음에 유의하면서 greedy하게 결정 문제를 $\mathcal{O}(N)$에 해결하면, 이분 탐색으로 $\mathcal{O}(N\log(\max(w_i)))$에 문제를 해결할 수 있습니다.
다음은 문제를 해결하는 예시 코드입니다.
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
constexpr i64 inf = 1LL << 60;
auto sol = [](int n, int k, auto adj) {
auto f = [&](i64 x) {
vector ret(0, 0);
auto rec = [&](const auto& self, int cur, int prv) -> pair<i64, i64> {
i64 mn = inf, mx = 0;
for (auto [nxt, cost] : adj[cur]) {
if (nxt == prv) continue;
auto [a, b] = self(self, nxt, cur);
if (b != -inf && b + cost > x) ret.push_back(nxt), a = 0, b = -inf;
if (a != inf) mn = min(mn, a + cost);
if (b != -inf) mx = max(mx, b + cost);
}
if (mn != inf && mn + mx <= x) mx = -inf;
return pair(mn, mx);
};
if (rec(rec, 1, 0).second != -inf) ret.push_back(1);
return ret;
};
i64 lo = -1, hi = i64(n) << 30;
while (lo + 1 < hi) {
i64 mid = lo + hi >> 1;
if (f(mid).size() > k) lo = mid;
else hi = mid;
}
vector ret = f(hi);
vector c(n + 1, 0);
for (int i = 0; i < ret.size(); i++) c[ret[i]] = 1;
for (int i = 1; i <= n; i++) {
if (c[i]) continue;
if (ret.size() == k) continue;
ret.push_back(i);
}
return pair(hi, ret);
};
int main() {
cin.tie(0)->sync_with_stdio(0);
int n, k; cin >> n >> k;
vector adj(n + 1, vector(0, pair(0, 0)));
for (int i = 1; i < n; i++) {
int a, b, c; cin >> a >> b >> c;
adj[a].push_back(pair(b, c));
adj[b].push_back(pair(a, c));
}
auto [res, buc] = sol(n, k, adj);
cout << res << '\n';
for (int x : buc) cout << x << ' ';
cout << '\n';
}
k-center problem의 최적해가 되는 정점의 부분 집합 $S$를 구성할 때, $k$보다 크기가 작은 집합이 구해질 수도 있는데, 이 경우에는 아무 정점이나 추가로 $S$에 포함시켜 크기를 $k$로 맞춰줘야 함에 주의해야 합니다.
5. Conclusion
지금까지 트리에서 k-center problem을 해결하는 효율적인 방법에 대해 알아보았습니다.
트리에서 k-center problem은 최적화 문제를 이분 탐색을 이용해 결정 문제로 바꾼 뒤, 결정 문제의 답을 교환 논증exchange argument를 이용하는 탐욕적 기법으로 선형 시간에 구하며 해결할 수 있습니다. 이러한 접근법은 기본적인 k-center problem 뿐만 아니라 BOJ 28219, BOJ 8213 등의 다양한 변형 문제로 유연하게 확장이 가능합니다.
k-center problem의 풀이와 같은 접근법은 ICPC나 KOI와 같은 주요 알고리즘 대회에서도 자주 등장하는 테크닉인 만큼, 본 포스트에서 다룬 증명 방식과 상태 전이 로직을 이해한다면 복잡한 트리 최적화 문제를 해결하는데 큰 도움이 될 것입니다.