Quantum Complexity
Introduction
계산 복잡도 이론(Computational Complexity Theory)을 처음 접할 때, 우리는 대개 튜링 머신(Turing Machine) 을 기준으로 정의된 클래스들을 마주하게 됩니다. 아마도 가장 친숙한 이름들은 다음과 같을 것입니다.
-
P: 결정론적 튜링 머신이 ‘다항 시간’ 내에 ‘풀’ 수 있는 문제들의 집합입니다. 보통 우리가 효율적으로 해결할 수 있는 문제라고 한다면 이 클래스에 속하는 문제들을 의미합니다.
-
NP: 비결정론적 튜링 머신이 ‘다항 시간’ 내에 ‘검증’할 수 있는 문제들의 집합입니다. 즉, 어떤 해답이 주어졌을 때, 그 해답이 올바른지 빠르게 확인할 수 있는 문제들을 포함합니다.
-
BPP: 확률적 튜링 머신이 ‘다항 시간’ 내에 ‘높은 확률’로 올바른 답을 내놓을 수 있는 문제들의 집합입니다. 이는 무작위성을 활용하여 효율적으로 문제를 해결하는 알고리즘들을 포함합니다.
-
PSPACE: 결정론적 튜링 머신이 ‘다항 공간’ 내에 문제를 해결할 수 있는 문제들의 집합입니다. 이는 시간보다는 공간(메모리) 사용량에 초점을 맞춘 클래스입니다.
이러한 튜링 머신 기반의 분류법은 문제를 해결하는데 필요한 시간적, 공간적 자원을 대략 파악하는 데 유용합니다. 그러나 우리가 사용하는 컴퓨터는 low-level 관점에서는 ‘회로(circuit)’로 구현되고 있습니다. 0, 1 bit를 나르는 선과 논리 게이트(AND, OR, NOT)로 구성된 회로를 상상해 봅시다. n개의 입력 비트를 사용한다면, 가능한 입력은 010100100… 이런 형태의 입력일 것입니다. 여기서 어떤 문제를 정의할 수 있을까요? 그리고 여기서 복잡도는 어떻게 정의될까요?
쉬운 문제를 살펴봅시다. 예를 들어, 입력 비트의 개수가 n일 때, 모든 비트가 0인지 확인하는 문제를 생각해 봅시다. 이 문제는 AND 게이트를 사용하여 쉽게 해결할 수 있습니다. n개의 입력 비트를 모두 AND 게이트에 연결하면, 출력이 1이 되는 경우는 오직 모든 입력이 1일 때뿐입니다. 따라서 이 문제는 매우 간단한 회로로 해결할 수 있습니다.
Classical Circuit Complexity
회로의 크기와 깊이
n개의 입력을 가지는 circuit에서 크기(size) 와 깊이(depth) 라는 두 가지 중요한 개념이 있습니다.
-
크기(size): 회로를 구성하는 게이트의 총 개수를 의미합니다. 만약 모든 게이트를 하나씩 순서대로 처리해야 한다면 순차적 실행 시간(Sequential Time) 과 유사한 개념이 됩니다. 즉, 알고리즘이 수행해야 하는 총 작업량을 의미합니다.
-
깊이(depth): 입력에서 출력까지 도달하는 데 필요한 최대 게이트 층의 수를 의미합니다. 병렬 처리가 가능하다면 실질적인 실행 시간에 더 가까운 개념입니다.
그럼 n개의 입력 비트가 주어졌을때 모든 비트가 1인지 확인하는 문제의 복잡도를 어떻게 될까요? 사용 가능한 게이트를 어디까지 허용하냐에 따라 달라집니다.

위 그림은 두 종류의 AND 게이트를 보여줍니다. 위에 있는 건 5-input AND gate입니다. 이걸 2-input AND 게이트로 구성한 모습이 아래에 있습니다.
만약 우리가 2-input AND 게이트 만 허용한다면, n개의 입력 비트가 모두 1인지 확인하는 문제를 해결하기 위해서는 log(n) 깊이의 회로가 필요합니다. 왜냐하면, 각 층에서 2개의 입력을 AND 연산하여 하나의 출력을 만들고, 이 출력을 다시 다음 층에서 AND 연산하는 과정을 반복해야 하기 때문입니다. 따라서 깊이는 log(n)이 됩니다. 회로의 크기는 n-1 입니다.
만약 우리가 임의 크기의 n-input AND 게이트 를 허용한다면, 이 문제는 깊이 1의 회로로 해결할 수 있습니다. 모든 입력 비트를 한 번에 AND 연산하여 출력할 수 있기 때문입니다. 회로의 크기는 1입니다.
이처럼 논리 게이트가 받을 수 있는 입력의 수가 제한이 없는 회로를 unbounded fan-in gate라고 부릅니다.
| 허용된 게이트 종류 | 회로 깊이 | 회로 크기 |
|---|---|---|
| bounded fan-in (2-input) | log(n) | n - 1 |
| unbounded fan-in | 1 | 1 |
이처럼, 회로의 복잡도는 사용 가능한 게이트의 종류에 따라 크게 달라질 수 있습니다.
PARITY 문제
이번에는 조금 더 복잡한 문제인 PARITY 문제를 살펴봅시다. PARITY 문제는 n개의 입력 비트 중에서 1의 개수가 홀수인지 짝수인지를 판단하는 문제입니다. 즉, 입력 비트의 합을 2로 나누었을 때 나머지가 1이면 홀수, 0이면 짝수입니다.
PARITY 문제를 AND, OR, NOT 게이트만으로 어떻게 해결할 수 있을까요? 사실, PARITY 문제는 이러한 게이트들만으로는 효율적으로 해결하기 어렵습니다. n-input XOR 게이트를 허용해 주면 한번에 되겠지만, 기본적으로 AND, OR, NOT 게이트만을 사용하는 게 원칙입니다 (나중에 AC, NC 클래스를 정의할 때 다시 다룹니다).
| 허용된 게이트 종류 | 회로 깊이 | 회로 크기 |
|---|---|---|
| bounded fan-in (2-input) | O(logn) | O(n) |
| unbounded fan-in | O(1) 불가능 | Poly(n) |
| unbounded fan-in | 2 | O($n2^n$) |
PARITY 문제는 회로 크기를 Poly(n) 으로 제한한다면 깊이 O(1) 로는 해결할 수 없음이 증명되어 있습니다[1]. 즉, PARITY 문제는 상수 깊이의 회로로는 해결할 수 없는 문제 중 하나입니다. 만약 깊이를 O($\log n$) 까지 허용한다면 아주 쉽게 풀립니다. (XOR 게이트를 트리 구조로 쌓으면 되니까요.)
만약 회로의 크기에 제한을 두지 않고 $O(n \cdot 2^n)$ 수준까지 허용한다면 깊이 2 만으로도 해결이 가능합니다 [2]. 이는 모든 함수를 ‘논리합의 논리곱(DNF)’ 형태로 표현하여, 가능한 모든 입력 조합에 대한 결과를 하드코딩하는 방식입니다. 그런데 회로 크기가 너무 커서 써먹을 수는 없습니다.
이처럼 회로 크기와 depth 사이에는 trade-off 관계가 존재하며, 특정 문제를 해결하는 데 필요한 최소 회로 깊이와 크기는 어떤 gate set을 허용하느냐에 따라 달라집니다.
AC, NC, LC, TC 클래스
모두 고전 회로를 의미합니다. 회로의 크기(게이트 수)는 Poly(n) 으로 제한합니다.
기본적으로 AND, OR, NOT 게이트를 사용합니다.
- AC: unbounded fan-in 게이트를 허용하는 회로 클래스입니다.
- AC$^0$: 크기 Poly(n)에 깊이는 상수 깊이만 가능합니다.
- AC$^1$: 크기 Poly(n)에 깊이는 $\text{O}(\log n)$ 까지 허용됩니다.
- AC$^2$: 크기 Poly(n)에 깊이는 $\text{O}(\log^2 n)$ 까지 허용됩니다.
- 즉 AC$^i$: 크기 Poly(n)에 깊이는 $\text{O}(\log^i n)$ 까지 허용됩니다.
- NC: bounded fan-in 게이트를 허용하는 회로 클래스입니다.
- NC$^0$: 크기 Poly(n)에 깊이는 상수 깊이만 가능합니다.
- NC$^i$: 크기 Poly(n)에 깊이는 $\text{O}(\log^i n)$ 까지 허용됩니다.
- TC: unbounded fan-in Threshold 게이트 (예: Majority gate)까지도 허용하는 회로 클래스입니다.
- TC$^0$: 크기 Poly(n)에 깊이는 상수 깊이만 가능합니다.
- TC$^i$: 크기 Poly(n)에 깊이는 $\text{O}(\log^i n)$ 까지 허용됩니다.
- LC: bounded fan-in 게이트를 허용하는 회로 클래스입니다. 회로의 깊이는 $\text{O}(n)$ 까지 허용합니다.
QAC, QNC, QLC, QAC$_f$ 클래스
~~대부분의 양자 컴퓨팅에서 사용되는 개념이 그렇듯이, ~~ 고전적인 회로 클래스에 대응되는 양자 회로 클래스들도 존재합니다.
양자 회로에서 unbounded fan-in gate란 여러 큐빗에 동시에 작용하는 (multi-controlled gate 를 의미합니다. 예를 들어, 고전 회로에서의 And 게이트에 대응되는 Toffoli gate가 있고, CZ 게이트 (controlled Z gate) 등등이 있습니다.
어차피 이런 기본적인 다중 큐빗 게이트들은 상수 깊이의 회로로 서로 환원되기 때문에, 표기상에 편의를 위해서 그냥 unbounded fan-in gate를 허용한다고 말하거나, 임의 크기 CZ 게이트를 허용한다고 기술하는 편입니다.
- QAC: unbounded fan-in 게이트를 허용하는 양자 회로 클래스입니다.
- QAC$^0$: 크기 Poly(n)에 깊이는 상수 깊이만 가능합니다.
- 즉 QAC$^i$: 크기 Poly(n)에 깊이는 $\text{O}(\log^i n)$ 까지 허용됩니다.
- QNC: bounded fan-in 게이트를 허용하는 양자 회로 클래스입니다.
- QNC$^0$: 크기 Poly(n)에 깊이는 상수 깊이만 가능합니다.
- 즉 QNC$^i$: 크기 Poly(n)에 깊이는 $\text{O}(\log^i n)$ 까지 허용됩니다.
- QLC: bounded fan-in 게이트를 허용하는 양자 회로 클래스입니다. 회로의 깊이는 $\text{O}(n)$ 까지 허용합니다.
양자 회로에는 Fanout gate라는 개념이 있는데, 이 unitary의 동작은 아래와 같습니다.
\[|x\rangle |y_1, y_2, ..., y_n\rangle \rightarrow |x\rangle |y_1 \oplus x, y_2 \oplus x, ..., y_n \oplus x\rangle\]양자 회로에서는 상태를 복사하는 것이 불가능하지만, Fanout gate 한 큐빗의 정보를 여러 큐빗에 전파하는 것이 가능합니다. Fanout gate는 직관적으로도 굉장히 강력해 보입니다. 이 Unitary를 CNOT gate로 naive하게 순차적으로 구현하려면 N개를 써야 합니다 (깊이 N). 더 효율적인 방법으로는 log(N) 깊이로도 구현할 수 있지만, 그래도 상수 깊이에서는 아직까지 구현하는 법이 알려져 있지 않습니다.
이제 Fanout 게이트를 허용하는 QAC 클래스인 QAC$_f$ 를 정의할 수 있습니다.
- QAC$_f$: unbounded fan-in 게이트와 Fanout 게이트를 허용하는 양자 회로 클래스입니다.
- QAC$^0_f$: 크기 Poly(n)에 깊이는 상수 깊이만 가능합니다.
- 즉 QAC$^i_f$: 크기 Poly(n)에 깊이는 $\text{O}(\log^i n)$ 까지 허용됩니다.
$QAC^0_f$ 는 굉장히 강력하단 것이 2005년에 밝혀졌는데[3], $QAC^0_f$ 는 Majority, Sorting, Arithematic operations, Phase estimation (따라서 QFT도 근사 가능) 등등을 계산할 수 있습니다.
Fanout, PARITY problem
Moore는 1999년에 그의 논문[4] 에서 다음과 같은 추측을 했습니다
QAC$^0$ 는 PARITY 문제를 해결할 수 없다.
즉, 상수 깊이, 다항 크기의 양자 회로로는 PARITY 문제를 해결할 수 없다는 것입니다. 이 추측은 아직까지 미해결 상태로 남아 있습니다.
재밌는 사실로는, PARITY를 푸는것과 Fanout 게이트를 구현하는 것은 동치라는 것입니다.
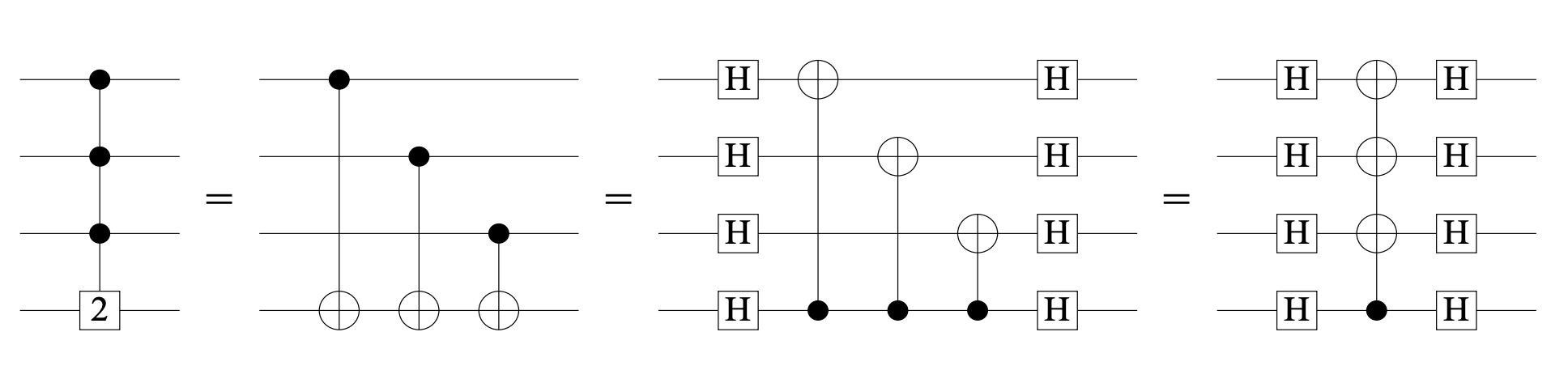
그림 2에서 이 사실을 직관적으로 나타내고 있습니다. PARITY는 n-1번의 CNOT게이트로 분해되고, CNOT게이트의 유명한 특징으로, 양쪽에 Hadamard gate를 넣으면 제어와 타겟이 바뀌는 특성이 있습니다. 따라서 PARITY 회로의 양쪽에 Hadamard 게이트를 넣으면 Fanout 회로가 되고, 반대로 Fanout 회로의 양쪽에 Hadamard 게이트를 넣으면 PARITY 회로가 됩니다.
즉 하나라도 상수 깊이로 구현한다면 다른 하나도 상수 깊이로 구현할 수 있다는 뜻입니다. 따라서 Moore의 추측은 다음과 같이 바꿔 쓸 수 있습니다.
QAC$^0$ 는 Fanout 게이트를 구현할 수 없다. 즉, $\text{QAC}^0 \subsetneq \text{QAC}^0_f$ 이다.
추측의 내용은 굉장히 단순합니다. 하지만 아직까지 이 추측을 증명하거나 반증할 수 있는 방법이 발견되지 않았습니다. $\text{QAC}^0$ 회로로 PARITY를 푸는것이 가능할 수도 있지만, 대부분의 사람들은 불가능할 것으로 추정하고 있습니다.
왜 사람들이 그렇게 추정하는지를 간략하게 소개하고 이 글을 마무리하겠습니다.
Pauli Degree
계산 복잡도를 논할 때, 보통 높은 차수라면 어렵고, 낮은 차수라면 쉬운 문제라고 생각합니다. 이 개념을 Boolean function에도 적용할 수 있습니다.
xor은 x+y mod 2이므로 두 입력 변수 x, y 에 대해 선형이지만, and는 xy 이므로 2차식입니다. Boolean function f: {0,1}^n → {0,1} 의 degree는 f를 표현하는 다항식 중에서 최고 차수를 의미합니다. 이를 좀 더 수학적으로 표현하면 Fourier analysis 가 나옵니다.
Fourier Analysis of Boolean Functions
고전적인 회로 복잡도 이론에서 Fourier 분석은 Boolean 함수의 특성을 이해하는 데 중요한 도구입니다. Fourier analysis를 편하게 하기 위해서 그동안은 boolean 값을 0,1 로 표현했지만, Fourier 분석에서는 이를 {-1,1} 으로 매핑합니다. 이때, 0은 1로, 1은 -1로 매핑합니다. 여기에는 두 가지 이유가 있습니다.
-
{0, 1} 에서의 합 (XOR)이 {-1, 1} 에서의 곱에 대응되게 하기 위함입니다.
-
0을 중심으로 값의 대칭성이 있어야 Fourier 분석이 더 편해지기 때문입니다.
Boolean 함수 f: {-1,1}^n → {-1,1} 는 입력 비트들의 조합에 따라 -1 또는 1을 출력하는 함수입니다. 이러한 함수는 다음과 같이 Fourier 급수로 표현될 수 있습니다. \(f(x) = \sum_{S \subseteq [n]} \hat{f}(S) \chi_S(x)\) 여기서 $\chi_S(x) = \prod_{i \in S} x_i$ 는 S에 속한 입력 비트들의 곱을 나타내는 기본 블럭같은 함수입니다. $\hat{f}(S)$ 는 Fourier 계수로, 함수 f의 해당 블럭의 성분을 나타냅니다. Fourier 계수는 다음과 같이 계산됩니다.
\[\hat{f}(S) = \frac{1}{2^n} \sum_{x \in \{-1,1\}^n} f(x) \chi_S(x)\]개념이 어려워 보여도, 그냥 내적을 새롭게 정의하고 orthonormal basis를 정의해서 해당 basis 위에서 좌표를 구하는 것과 같습니다.
$2^n$ 차원 공간이기 때문에, basis도 $2^n$ 개가 필요하고, 위에서 설명한 $\chi_S$ orthonormal basis를 형성합니다. 내적 $\chi, \psi$ 를 다음과 같이 정의합니다.
\[\langle \chi, \psi \rangle = \frac{1}{2^n} \sum_{x \in \{-1,1\}^n} \chi(x) \psi(x)\]아래 두가지 사실은 쉽게 확인할 수 있습니다.
- $\langle \chi_S, \chi_T \rangle = 0$ if $S \neq T$
- $\langle \chi_S, \chi_S \rangle = 1$
따라서 $\chi_S$ 들이 orthonormal basis를 형성합니다. 따라서 주어진 함수 f에 대해서, basis 위에서의 좌표 (Fourier 계수) 를 구하려면 단순히 내적을 취하면 됩니다. 위에서 Fourier 계수를 구하는 식이 바로 그것입니다.
Example: And gate
한번 입력 3개짜리 and 게이트를 Fourier 분석해 봅시다. $f(x_1, x_2, x_3) = x_1\text{ AND }x_2\text{ AND }x_3$ 라고 표현됩니다. 이제 이를 {-1,1} 표현으로 바꿔 봅시다. and 게이트는 모든 입력이 -1일 때만 -1을 출력하고, 나머지 경우에는 1을 출력합니다. 따라서 다음과 같이 쓸 수 있습니다.
\[f(x_1, x_2, x_3) = 1 - \frac{1}{4}(1 - x_1)(1 - x_2)(1 - x_3)\]이 식을 전개했을때 나오는 Fourier 계수는 다음과 같습니다.
- $\hat{f}(\emptyset) = \frac{3}{4}$
- $\hat{f}({1}) = \frac{1}{4}$
- $\hat{f}({2}) = \frac{1}{4}$
- $\hat{f}({3}) = \frac{1}{4}$
- $\hat{f}({1,2}) = -\frac{1}{4}$
- $\hat{f}({1,3}) = -\frac{1}{4}$
- $\hat{f}({2,3}) = -\frac{1}{4}$
- $\hat{f}({1,2,3}) = \frac{1}{4}$
따라서, 이 boolean function의 degree는 3 입니다.
좌표계에서 각 성분의 제곱의 합은 벡터의 norm의 제곱과 같기 때문에, 아래 식이 성립합니다. \(\frac{1}{2^n} \| A \|_F^2 = \frac{1}{2^n} \sum_{x \in \{0,1\}^n} \langle x | A^\dagger A | x \rangle = \sum_{P \in \mathcal{P}^n} \hat{A}(P)^2\)
또한, Boolean에서 각 차수가 어느 비율로 포함되어 있는지를 계산하고 싶다면
\[\text{W}^{=k}(f) = \sum_{S: |S| = k} \hat{f}(S)^2\]식을 사용하면 됩니다. 위의 And 게이트 예시에서, 3차 성분의 비율을 구해 봅시다.
\[\text{W}^{=3}(f) = \hat{f}(\{1,2,3\})^2 = \left(\frac{1}{4}\right)^2 = \frac{1}{16}\]고차수에 엄청 집중되어 있지는 않다는 것을 알 수 있습니다.
Example: PARITY
이제, PARITY 문제가 왜 어려운지 알아봅시다. PARITY함수를 Fourier 분석해 본다면,
\[PARITY(x) = x_1 x_2 ... x_n\]그냥 모든 항의 곱셈으로 표현됩니다. -1이 홀수개일 때만 -1을 출력하고, 애초에 PARITY는 {0, 1} 표현에서 XOR이었기 때문에 {-1, 1}에서는 곱셈으로 표현됩니다.
따라서 Fourier weight은 아래와 같습니다.
\(\text{W}^{\lt n}(PARITY) = 0\) \(\text{W}^{= n}(PARITY) = 1\)
모든 성분이 n차 항에 몰려 있습니다. 즉, PARITY 함수는 최고 차수에만 집중되어 있기 때문에, 낮은 차수로는 표현하기가 매우 어렵습니다. 이것이 바로 PARITY 문제가 회로 복잡도 이론에서 어려운 문제로 간주되는 이유 중 하나입니다.
Low degree concentration in QAC$^0$
QAC$^0$가 PARITY를 풀지 못한다고 증명하기 위해 유용한 접근 방식은 아래 2 step을 따릅니다.
- 고차수의 boolean function은 낮은 차수의 함수로 근사하기 어렵다.
- QAC$^0$ 의 출력은 낮은 차수에 집중되어 있다.
하지만 이 방식으로도 아직 Moore의 추측을 증명하지는 못했습니다. 다만, QAC$^0$ 의 출력이 낮은 차수에 집중되어 있다는 점은 여러 연구를 통해 입증되었습니다[5,6].
Moore의 추측은 25년 넘도록 풀리지 않았지만, 최근 대부분의 진전은 1~2년 사이에 이루어졌습니다. 조만간 이 문제에 대한 결정적인 결과가 나올지도 모릅니다.
References
[1] Furst, Merrick, James B. Saxe, and Michael Sipser. “Parity, Circuits, and the Polynomial-Time Hierarchy.” Mathematical Systems Theory, vol. 17, no. 1, 1984, pp. 13 to 27.
[2] Arora, Sanjeev, and Boaz Barak. Computational Complexity: A Modern Approach. Cambridge University Press, 2009. Ch. 6.
[3] Høyer, Peter, and Robert Špalek. “Quantum Fan-out Is Powerful.” Theory of Computing, vol. 1, no. 5, 2005, pp. 81 to 103. doi:10.4086/toc.2005.v001a005.
[4] Moore, Cristopher. “Quantum Circuits: Fanout, Parity, and Counting.” arXiv, 17 Mar. 1999, arXiv:quant-ph/9903046.
[5] Nadimpalli, Shivam, et al. “On the Pauli Spectrum of QAC0.” arXiv, 16 Nov. 2023, arXiv:2311.09631.
[6] Anshu, Anurag, et al. “On the Computational Power of QAC0 with Barely Superlinear Ancillae.” arXiv, 9 Oct. 2024, arXiv:2410.06499.