leejseo's profile image

leejseo

January 16, 2026 00:00

1. 서론

지난 글에서는 $\mathcal{F}$-deletion 문제의 FPT(Fixed-parameter tractable) 알고리즘에 대해 살펴보았다. 해당 알고리즘은 treewidth가 $t$ 이하로 bounded인 그래프에서 $2^{2^{O(t \log t)}} n$ 시간에 동작하였다.

$\mathcal{F}$-(M-)deletion 문제는 널리 믿어지는 Exponential Time Hypothesis 하에서 일반적인 그래프 클래스($\mathcal{F}$가 chair 및 banner로 불리는 작은 크기의 그래프의 contraction으로 나타낼 수 없는 연결 그래프를 포함하는 경우)에 대해 $2^{o(t \log t)} poly(n)$ 시간에 해결될 수 없음이 밝혀져 있다. 이 글에서는 2023년 논문 [1]에서 제시한 $2^{O(t \log t)} n$ 시간에 $\mathcal{F}$-(M-)deletion 문제를 해결하는 알고리즘을 소개한다.

2. 글의 구성

이 글에서 소개할 알고리즘 자체는 지난 글에서 소개한 FPT 알고리즘과 상당히 유사하다. 하지만, 시간 복잡도에 영향을 주는 요소들에 대한 더욱 정교한 분석을 포함하고 있고, 이와 관련하여 Graph Minor Theory의 결과들을 상당히 많이 활용한다. 따라서, 이 글은 크게 다음과 같은 요소들로 구성된다.

• 3장: 문제 정의
• 4장: 알고리즘
• 5장: Representative의 treewidth가 너무 클 수 없는 이유
• 6장: Representative가 너무 클 수 없는 이유
• 7장: 알고리즘 분석 및 결론

논문이 상당히 난해한 만큼, 디테일을 다루기보다는 논문을 이해하기 위해 필요한 요소들을 종합적으로 담은 글로 구성하고자 하였다. 이 글을 읽고 나서 세부적인 증명의 디테일이 궁금하다면 [1]을 읽어보는 것을 추천한다. [1]을 바로 읽는 것보다는 훨씬 수월하리라 확신한다.

3. 문제 정의

지난 글에서 소개한 알고리즘과 풀고자 하는 문제도 당연히 동등하고, 마찬가지로 boundaried graph와 folio 등의 개념은 여전히 활용한다. 다만, 세부적인 정의에서 약간 다른 부분이 있다.

$\newcommand{\F}{\mathcal{F}}\mathcal{F}$-M-DELETION: 그래프 $G$와 유한개의 그래프를 모아 놓은 $\mathcal{F} $가 주어졌을 때 $G\setminus S$가 $\F$의 원소를 minor로 포함하지 않도록 하는 $\vert S \vert \le k$가 존재하는가?

$\F$-TM-DELETION: 그래프 $G$와 유한개의 그래프를 모아 놓은 $\F$가 주어졌을 때 $G\setminus S$가 $\F$의 원소를 topological minor로 포함하지 않도록 하는 $\vert S \vert \le k$가 존재하는가?

두 문제를 푸는 것은 사실상 동등함을 관찰할 수 있다. 왜냐하면, 어떤 그래프 $H$가 $G$의 minor임은 $H$를 minor로 가지는 그래프 가운데 topological minor-wise minimal 한 것 중 $G$의 topological minor가 존재함과 동치이기 때문이다.

4. 알고리즘

알고리즘에 대해 본격적으로 살펴보기에 앞서, 알고리즘을 설명하기 위해 필요한 개념들을 살펴보자.

이 글 전체에 걸쳐 $\mathcal{F} $를 하나 고정해두었다고 가정하자.

$h$는 $\F$에만 의존하는 어떤 상수이고(나중에 정의됨), $t$는 입력으로 주어지는 그래프의 treewidth 정도의 수라고 하자. $\Theta(tw)$ 스케일이라고 생각하면 된다. $t$가 실제로 그런 수임이 중요해지는 부분에서는 명시적으로 treewidth에 대해 언급할 것이다. 그래프는 무향 그래프를 의미한다.

Boundaried Graph

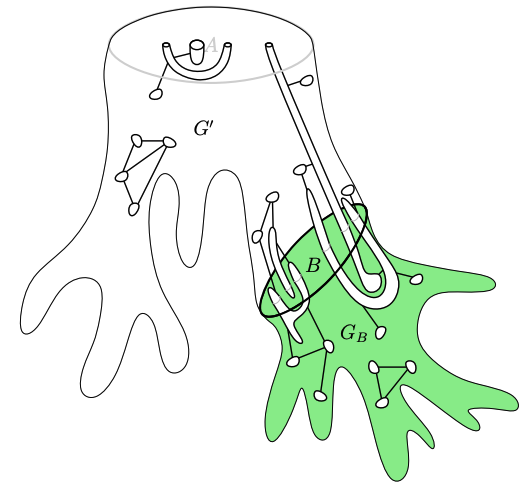
$t$-boundaried graph란 그래프 $G$, boundary set $B \subseteq {V(G) \choose t}$, 그리고 bijection $\rho : B \to [t]$ 로 구성된 순서쌍 $\newcommand{\G}{\mathbf{G}} \G:= (G, B, \rho)$를 의미한다. 우리는 모든 그래프들을 boundaried graph의 관점에서 살펴볼 것이다.

Boundary는 그래프의 경계로, 우리는 boundary가 똑같이 생겨 먹은 그래프들을 ‘붙이는’ 연산을 다룰 것이다. Boundary set의 크기가 같은 boundaried graph $\G_1, \G_2$ 의 gluing operation $\G_1 \oplus \G_2$ 는 $\rho_2^{-1} \circ \rho_1$ 이 $G_1[B_1] $ 과 $G_2[B_2]$ 사이의 graph isomorphism 일 때만 정의되며, boundary를 이어붙여서 생긴 새로운 graph가 연산의 결과물로 정의된다. Formal하게는, $G_1$ 과 $G_2$의 disjoint union을 취한 후 대응 되는 boundary vertex를 identify 하여 생기는 결과물을 의미한다.

$\G$와 gluing operation이 잘 정의되는 boundaried graph를 $\G$와 compatible 하다고 부르자.

Boundary를 제외한 그래프의 ‘세부적인’ 구성요소들을 그래프의 detail이라 부를 것이고, 수식으로는 $detail(\G) := \max { \vert E(G) \vert, \vert V(G) \setminus B \vert }$로 정의된다.

Boundary가 ‘동일하게 생긴’ 두 boundaried graph $\G_1, \G_2$에 대해 equivalence relation $\equiv_h$를

• $\G_1 \equiv_h \G_2$ 임은
• 임의의 vertex, edge가 각 $h$개 이하인 graph $H$와 임의의 ($\G_1, \G_2$와) compatible 한 $\mathbf{F}$ 에 대해 $H \preceq_{m} \mathbf{F} \oplus \G_1 \iff H \preceq_{m} \mathbf{F} \oplus \G_2$ 를 만족함으로

정의하자. (여기에서, $G\preceq_{m} H$ 는 $G$가 $H$의 minor 임을 의미하는 relation이다.)

Folio

우리는 $\equiv_h$의 equivalence class를 직접적으로 관리하며 동적 계획법을 사용하고 싶지만, 이를 직관적으로 다루는 것은 어려운 일이다. 그래서 folio를 정의한다.

Boundaried graph $\G = (G, B, \rho)$ 의 $h$-folio를 $\newcommand{fol}{\mathsf{-folio}} h\fol (\G) := { \G’ \mid \G’ \preceq_{tm} \G, \G’\text{has detail at most }h }$ 로 하여 정의하자. (여기에서, $\preceq_{tm}$ 은 topological minor relation으로, boundaried graph 에서는 boundary vertex 를 ‘안 건드리고’ subdivision을 subgraph로 가짐으로 하여 정의된다.)

같은 $h\fol$ 을 가지는 그래프는 $\equiv_h$ 에 대해 같은 equivalence class 에 속함을 관찰할 수 있다. 즉, folio는 $\equiv_h$ 의 refinement가 된다.

동일한 $h\fol$ 을 가지는 $t$-boundaried graph 중 가장 크기가 작은 것을 representative로 뽑고, 이것을 모아놓은 집합 $\mathcal{R}_h^{(t)}$ 을 고려하자.

알고리즘

지난 글에서 소개한 알고리즘과 동일하지만, 글의 완결성을 위해 조금 더 상세히 설명하겠다.

입력으로 주어지는 그래프의 rooted branch decomposition을 고려할 것이다. 자세한 정의는 이전 글을 참고하면 좋고, 요약은 아래 이미지를 참고하면 좋다.

Branchwidth와 treewidth 값은 선형적인 관계에 있음이 알려져 있으며(즉, 어느 하나가 bound 되어 있다면, 다른 하나 또한 그의 상수배 이내의 값을 가진다), rooted branch decomposition에 대해 다음의 사실도 관찰할 수 있다.

• $bw(\G) \le bw(G) + \vert B \vert$

이를 기반으로, 다음과 같은 알고리즘을 생각할 것이다.

1. $2^{O(t)} n$ 시간에 $(G, \emptyset, \emptyset)$ 의 rooted branch decomposition을 계산한다.

2. 각 간선 $e$에 대해 DP 테이블을 정의할 것인데, 다음의 의미를 지니는 두 인자를 고려하자:

   • $L \subseteq B_e$: $B_e$ 의 정점 가운데 ‘삭제’ 된 정점을 표현
   • $C$: $\G_e$ 를 적절히 건드린 후 남은 부분의 folio

   $D_e(L, C)$ := $\G_e$에서 정점의 subset을 삭제할 때, $B_e$ 중 $L$ 만 삭제되고, $C$를 결과물의 folio로 할때 지워야 하는 정점의 최소 개수

3. 이 테이블은 다음과 같이 채울 수 있다:

   • 리프 노드인 경우: $V(\G_e) = \Theta(1)$ 이므로, 상수 시간에 브루트포스로 채울 수 있다.

   • 리프 노드가 아닌 경우: 다음의 pseudo-code로 채울 수 있다.

     • for $(L_1, C_1) $ of $T_{e_1}$

       • for $(L_2, C_2)$ of $T_{e_2}$

         • 만약 두 시나리오를 합치는게 모순을 일으키지 않는다면,

           $T_e(L, C) = \min(T_e(L, C), T_{e_1}(L_1, C_2) + T_{e_2}(L_2, C_2) - \vert L_1 \cap L_2 \vert )$

시간 복잡도를 살펴보자. 한 간선 $e$에 대해 $T_e(\cdot, \cdot)$ 의 entry의 수는 $\vert \mathcal{R}_h^{(t)} \vert \cdot 2^{O(t)}$ 가 된다. 따라서, 두 테이블을 머지 하는 것은 $2^{O(t)} \cdot \vert \mathcal{R}_h^{(t)} \vert ^2$ 시간에 가능하며, 전체 간선이 $\le tn$ 개 있으므로, 알고리즘은 $2^{O(t)} \cdot \vert \mathcal{R}_h^{(t)} \vert ^{O(1)} \cdot n$ 시간에 동작한다.

Claim. $\vert \mathcal{R}_h^{(t)} \vert = 2^{O_h(t \log t)}$.

위 Claim이 이후 장에서 우리가 살펴볼 주된 내용이며, 이 claim은 다음을 imply 한다.

Theorem. 알고리즘은 $2^{O_h(t \log t)} \cdot n$ 시간에 동작한다.

5. Representative의 treewidth가 너무 클 수 없는 이유

이 장에서 우리는 representative의 treewidth가 너무 클 수 없음을 확인할 것이다.

Flat Wall Theorem. $G$가 $K_q$를 minor로 가지지 않는 graph라 하고, $r$이 홀수라고 하자. 다음 중 최소 하나가 성립한다.

1. $G$의 treewidth가 $O_q(r)$ 이다.
2. 크기가 $O_q(1)$ 인 $A \subseteq V(G)$ 가 존재해서, $G\setminus A$에 높이 $r$인 flat wall이 존재한다.

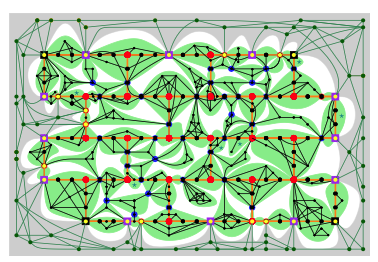
높이 $r$인 벽돌 형태의 구조를 $r$-wall이라고 부르고, 위 그림처럼 예쁘게 위치해 있으면 flat wall을 가진다고 부른다. 위 그림에서 빨갛게 표시된 부분이 flat wall이라고 생각하면 된다.

Flat Wall Theorem은, 다시 말해, treewidth가 큰 graph에는 작은 boundary와 그에 의해 touch 되지 않는 영역의 flat wall이 존재함을 말한다. Flat Wall 이라는 structure가 주는 좋은 성질 때문에 우리는 많은 것을 논할 수 있다.

Representative graph의 treewidth가 아주 크다고 가정하자. 그러면, representative graph는 Flat Wall Theorem에 의해, 아주 큰 flat wall을 가지게 될 것이다.

아주 큰 wall 안에서, 우리는 동심원 형태를 이루는 아주 많은 cycle과 이를 가로지르는 아주 많은 path를 찾을 수 있을 것이다. (Cycle의 경우, wall의 테두리를 한 층 씩 차례로 벗겨낸다고 생각하면 좋다.) 이 구조를 railed annulus라 부른다.

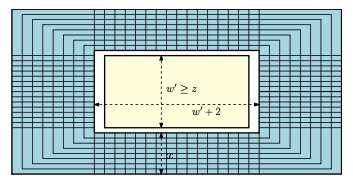
Representative graph 위에서 우리가 찾는 minor $H$는 크기가 고정된 상수 $h$이다. 반대로, 우리가 찾은 railed annulus는 아주 크다. 따라서, minor model을 올려놓는 것 만으로 이 annulus를 전부 덮을 수 없다.

그리고 railed annulus는 cycle과 rail이 직교하는 예쁜 구조를 이루고 있기 때문에, 아무리 복잡한 topological minor model을 이 위에 올려놓더라도 model 상에서의 subdivision path들이 특정한 rail을 따라가는 등 예쁜 형태를 강제할 수 있다.

또한 아주 큰 wall 안에서는 wall의 조각(brick)들이 가지는 folio가 모두 같아지는 충분히 큰 subwall이 존재한다는 사실도 Flat Wall 관련 이론의 결과로 알려져 있다. 논문에서는 이 사실을 활용하여 wall의 가장 중심부를 지나도록 놓인 minor model을 ‘조금 더 바깥쪽’의 같은 folio를 가지는 brick 쪽으로 밀어내는 기법을 논한다.

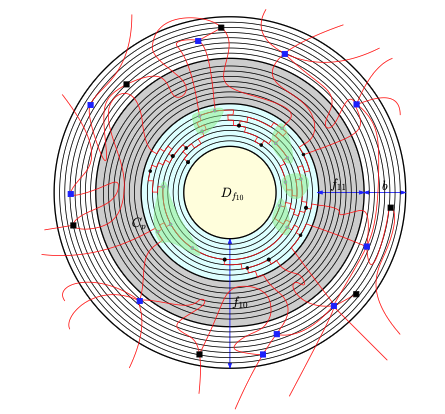
이 과정을 통해 우리는 결론적으로, representative가 가지는 flat wall의 가장 가운데 부분에 있는 어떤 정점 $v$를 지우더라도 representative 위에 minor model을 올려놓는 데 아무런 영향을 주지 않는다는 사실에 도달한다. 이는 representative를 가장 크기가 작게 잡은 것에 모순이다.

따라서, representative는 아주 큰 treewidth를 가질 수 없을 뿐더러, representative 안의 아주 큰 flat wall들을 전부 ‘망가뜨리는’ 작은 set이 존재한다. 심지어 parameter 조정을 잘 하면 Graph 자체의 boundary가 이런 현상을 만들도록 할 수 있다.

Lemma 1. $\G = (G, B, \rho)$가 $\mathcal{R}_h^{(t)}$ 의 boundaried graph 라면, $B$가 모든 큰 flat wall을 망가뜨린다.

6. Representative가 너무 클 수 없는 이유

우리는 representative의 treewidth가 클 수 없음은 물론, 그 안의 모든 복잡한 구조(large flat wall)들이 크기 $t$짜리 boundary $B$에 의해 망가진다는 사실을 확인했다.

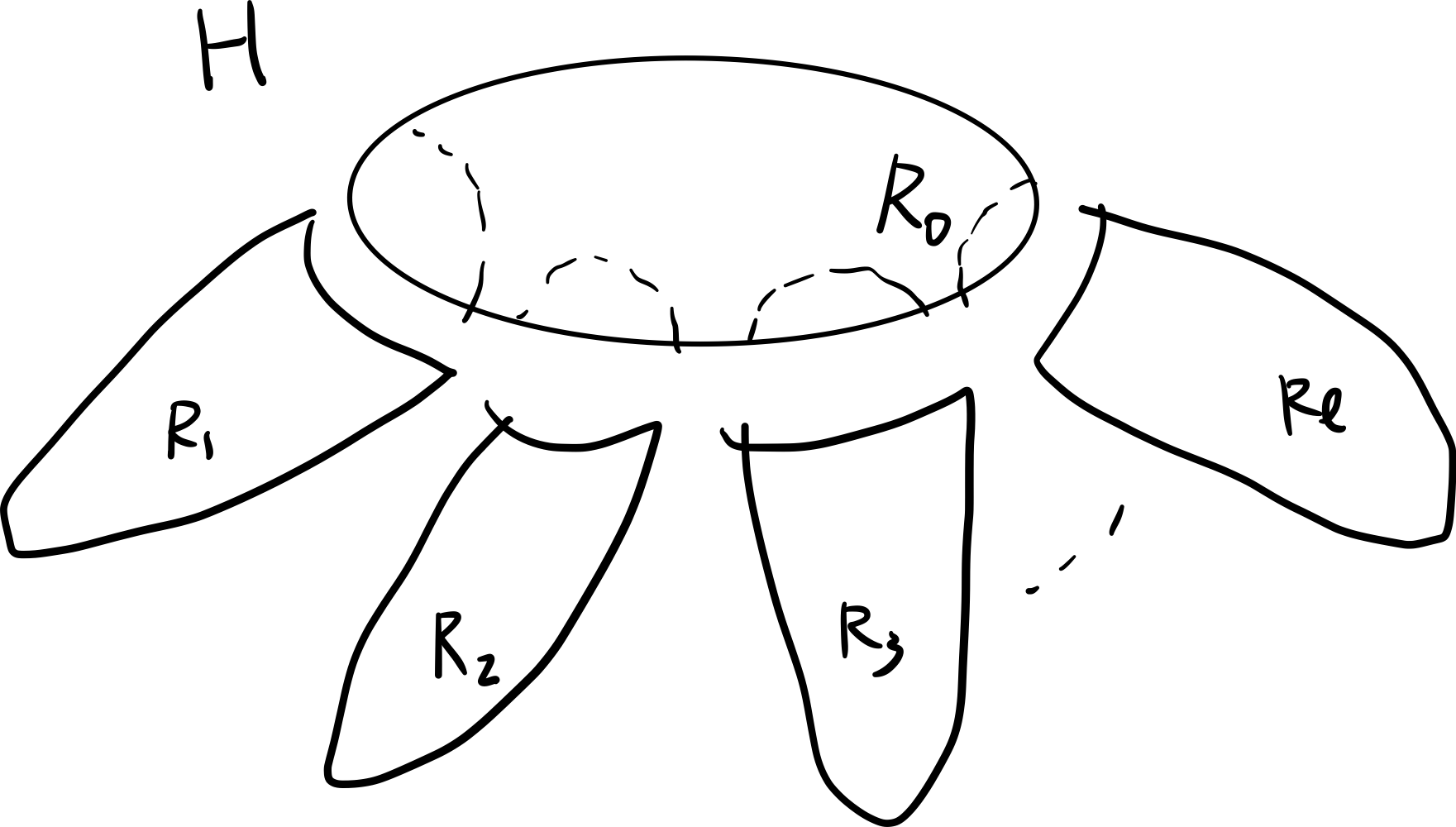
그런데, Graph Minor Theory의 결과로 Protrusion Decomposition이 존재함이 알려져있다. 이를 블랙 박스로 쓰면, 우리는 representative $H$가 $R_0$ 및 이를 둘러싼 $R_1, R_2, \cdots, R_{l}$, 이렇게 $l+1$ 개의 집합으로 partition 됨을 얻게 되는데,

• $\vert R_0 \vert \le O_\mathcal{F}(t)$, $l \le O_\mathcal{F}(t)$,
• $\vert R_i \vert \le O_\mathcal{F}(1)$

의 성질을 함께 얻게 된다. 이는 곧 $\mathcal{R}h^{(t)}$에 속하는 그래프들이 최대 $O{\mathcal{F}}(t)$ 개 이내의 정점을 가짐을 의미한다.

게다가, $\mathcal{R}_h^{(t)}$의 그래프들은 다음과 같이 두 종류로 나눌 수 있다:

• $K_h$ : 이 분류에 속하는 그래프는 $K_h$ 단 1개이다.
• $K_h$-minor-free: 이 분류에 속하는 그래프는 최대 $O_{\mathcal{F}}(t)$ 개의 간선만을 가질 수 있음이 Graph Minor Theory의 결과로 알려져있다.

정점 $n$개, 간선 $m$개를 가지는 그래프가 ${n^2 \choose m} = 2^{O(n \log m)}$개 있으므로, $\mathcal{R}_h^{t}$의 크기 역시 $2^{O(t \log t)}$로 bound됨을 알 수 있다.

7. 결론

결론적으로, 우리는 Graph Minor Theory의 결과들에 의해

• representative의 treewidth가 크면 large flat wall이 존재하고, 그 정 가운데의 정점은 ‘지워도 되는’ 정점이라 최소성에 모순이 발생하고,
• representative의 treewidth가 bound 됨 및 기타 유용한 성질들로 부터 protrusion decomposition이 존재하므로,
• representative의 정점 수가 bound 되고,
• 그러므로 representative set의 크기 역시도 $2^{O_{\mathcal{F}}(t \log t)}$ 로 bound 된다는 사실을 확인하였다.

이로부터 알고리즘의 시간 복잡도가 $2^{O_{\mathcal{F}} (t \log t)} \cdot n$ 임을 살펴보았다.

여담으로, 2월 초에 이 논문을 해설하는 talk을 할 예정이고, 깊은 디테일을 담은 관련 자료가 정리되면 추후 첨부할 수 있도록 하겠다.

Reference

Reference의 그림들도 활용했음을 밝혀둔다.

[1] J. Baste et. al (2023). Hitting Minors On Bounded Treewidth Graphs IV: An Optimal Algorithm. Siam J. Comput. Vol. 52, No. 4, pp. 865-912

[2] https://www.lirmm.fr/~sau/talks/IMPA-2019-Ignasi.pdf