defwin's profile image

defwin

January 29, 2026 00:00

0. Introduction

상전이(phase transition)는 물리학에서 나온 개념으로, 어떤 임계점을 기준으로 양쪽에서 행동이 달라지는 것을 말합니다. 물리학을 공부하는 경우 이러한 현상을 학습하게 되는데요, 대표적인 예시로 2차원 이징 모델이나 란다우 긴즈버그 모델 등이 있습니다. 놀랍게도 어떤 랜덤하게 구성한 네트워크들에 대해서도 이와 비슷한 상전이 현상이 일어남이 알려져 있습니다.

이전 글에서는 랜덤 네트워크 모델 중 모든 가능한 간선들이 연결되어있을 확률이 $p$로 일정한, 가장 간단한 모델인 Erdős–Rényi 모델에서 일어나는 상전이에 대해 알아보았습니다. 또한 이 모델이 클러스터링 문제(두 이웃이 서로 이웃일 확률이 0에 수렴)나 실제 세계의 네트워크를 잘 표현하지 못하는 등의 근본적인 한계를 가지고 있음도 지적하였습니다.

이에 본 글에서는 차수 분포가 큰 수에서 Power law distribution를 따를 때, 즉 차수 분포가 큰 수에서 다음을 따르는 분포를 살펴보고자 합니다.

\[p_k \sim k^{-\gamma}\]

이런 네트워크를 scale-free network라고 부르는데요, 그 이유는 이 네트워크의 대푯값들의 절대적인 크기가 중요하지 않기 때문입니다. 이는 통계물리적인 측면에서 물리를 기술하는 scale을 변환시키는 재규격화 측면에서 해당 문제를 처음 접근했기 때문으로 보입니다. 이 scale-free network는 많은 실제 세계의 네트워크들과 비슷한 양상을 보임이 알려져 있습니다.

Scale free network는 Erdős–Rényi 모델과는 접근법에서 큰 차이가 있어야 하는데요, 이는 노드가 존재할 확률이 균등하지 않기 때문입니다. 추후에 보게 되겠지만 generating function 기법을 도입하여 이 문제를 해결할 수 있습니다.

본 글은 KIAS-SNU Physics Winter Camp 2025 중 고등과학원 계산과학부 이덕선 교수님의 “Phase Transitions in Networks” 강의 및 group project 참여 중 공부한 내용을 바탕으로 함을 알립니다.

1. Branching Process Approach

Erdős–Rényi 모델에서처럼 GCC에 포함된 노드를 살펴보는 것보다는 GCC에 포함되지 않는 노드를 조사하는 편이 편할 것으로 예상할 수 있습니다. 다만 Erdős–Rényi 모델에서는 임의의 노드를 골라도 해당 노드가 GCC에 연결되어있지 않을 확률이 동일하여 조금 더 쉽게 접근이 가능했지만, 이 경우에서 같은 방법을 적용하는 것은 어려워보입니다. 그러므로 더 일반적으로 적용 가능한, 차수 분포만 주어진 랜덤 그래프에서 GCC의 크기를 구하는 방법을 알아보는 것이 좋아 보입니다.

$P(s)$를 임의의 노드를 골랐을 때 해당 노드가 크기 $s$인 작은 연결요소를 만들 확률이라고 합시다. $\sum_s P(s)$가 작은 연결 요소에 포함될 확률이 되므로, GCC의 비율 $m=1-\sum_s P(s)$이 됨을 알 수 있습니다. 즉, $P(s)$를 알아내기만 한다면 $m$도 구할 수 있으므로 $P(s)$를 branching process를 통해 구해봅시다.

모든 연결이 트리임을 가정하고, 아래와 같은 상황에서 1번 노드에 집중합시다. 여기서 트리임을 가정해도 괜찮은 이유는 GCC가 생성되는 임계점 근처에서 엣지가 충분히 많지 않아 사이클이 생성되는 경우가 많지 않다고 생각할 수 있기 때문입니다.

그림 1. Branching process

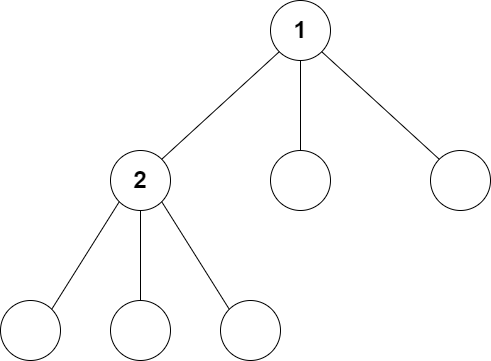
1번 노드가 차수 $s$인 연결요소를 만든다는 것을 알아보기 위해서는, 연결된 다른 노드들의 차수를 살펴봐야 합니다. $R(s)$를 한 노드에 연결된 다른 노드를 루트로 하는 서브트리의 크기 분포라 합시다. 차수 분포를 $p_k$라 했을 때 다음이 성립함을 알 수 있습니다.

\[P(s)=\delta_{s,1}p_0 + \sum_{k \geq 1} p_k \prod_{i=1}^{k}\sum_{s_i=1}^{\infty} R(s_i) \delta_{s_1+\cdots+s_k,s-1}\]

여기서 $\delta_{i,j}$는 $i$와 $j$가 같은 경우 1, 아닌 경우 0을 의미하는 기호입니다. 첫 델타 항은 차수가 1인 경우 차수가 0인 경우밖에 없으므로 이를 고려해준 것이고, 이후 항은 1번 노드가 차수 $k$인 경우에서 $i$번째 자식이 $s_i$의 서브트리 크기를 가지는 경우에 대한 확률을 모두 더해준 꼴임을 알 수 있습니다.

지난 글에서 다루었듯이 2차 초과 차수 분포(어떤 노드의 자식의 자식 수 분포. 그림에서 예를 들면 1번 노드 기준 2번 노드의 자식 수)는 $r_k = (k+1)p_{k+1}/\langle k \rangle$로 주어지므로, 비슷하게 다음이 성립함을 알 수 있습니다.

\[R(s)=\delta_{s,1}r_0 + \sum_{k \geq 1} r_k \prod_{i=1}^{k}\sum_{s_i=1}^{\infty} R(s_i) \delta_{s_1+\cdots+s_k,s-1}\]

2. Generating Functions

위에서 얻은 $P(s)$와 $R(s)$에 대한 두 식은 너무 복잡하여 제대로 된 계산을 해보기 힘들게 생겼습니다. 여기서 이 분포로 생성되는 생성함수(generating function)을 구해보면, 놀랍게도 깔끔하게 정리됩니다. 다음과 같이 생성함수들을 정의하겠습니다.

\[g(\omega)=\sum_{k=0}^{\infty} p_k\omega^k, \quad h(\omega)=\sum_{k=0}^{\infty} r_k\omega^k\] \[\mathcal{P}(z)=\sum_{s=1}^{\infty} P(s)z^s, \quad \mathcal{R}(z)=\sum_{s=1}^{\infty} R(s)z^s\]

이를 이용하여 $\mathcal{P}(z)$를 정리해보면 다음과 같습니다.

\[\mathcal{P}(z) = p_0z + z \sum_{k \geq 1} p_k\prod_{i=1}^{k} \sum_{s_i=1}^{\infty} \mathcal{R}(s_i)z^{s_i} = z\left[p_0 + \sum_{k \geq 1} p_k R(z)^k \right] = zg(\mathcal{R}(z))\]

$\mathcal{R}(z)$도 비슷하게 얻을 수 있습니다.

\[\mathcal{R}(z) = zh(\mathcal{R}(z))\]

이전에 언급했듯이 GCC의 비율은 $m=1-\sum_s P(s)$이고, 생성함수를 이용하면 이를 $m=1-\mathcal{P}(1)$로 나타낼 수 있습니다. $z=1$을 $\mathcal{P}(z)$와 $\mathcal{R}(z)$에 대입해보면 다음 두 식을 얻습니다.

\[\mathcal{P}(1) = g(\mathcal{R}(1)),\quad \mathcal{R}(1) = h(\mathcal{R}(1))\]

$g$와 $h$를 분석한 뒤 오른쪽 방정식을 풀기만 하면 자동적으로 $m$도 구할 수 있게 됨을 알 수 있습니다. GCC가 존재하지 않을 조건은 $\mathcal{P}(1)=1$인데요, $g(1)=h(1)=1$임을 생각해보면 이는 $\mathcal{R}(1)=1$임과 동치임을 알 수 있습니다. 즉 이 해만 존재하는 경우가 GCC가 존재하지 않는 경우에 대응된다는 것을 알 수 있습니다.

3. Critical Point and Critical Exponents

이제 구체적으로 어떤 상태가 GCC의 존재 여부를 결정하는 임계점인지 알아보겠습니다. 임계점 근처에서는 $\mathcal{R}(1)$이 처음으로 1을 벗어나는 해가 생기므로, 어떤 작은 $u$에 대해 해가 $\mathcal{R}(1)=e^{-u}$꼴이라고 가정하겠습니다. 먼저 $\mathcal{P}(1)$을 살펴보면

\[\mathcal{P}(1) = g(e^{-u}) = \sum_k p_k e^{-ku} \approx \sum_k p_k(1-ku) = 1 - \langle k \rangle u\]

따라서 $m=1-\mathcal{P}(1)\approx \langle k \rangle u$이 됩니다. 즉, $u$의 행동을 알아내기만 하면 임계값 근처에서의 GCC 크기의 행동을 알아낼 수 있으므로 $u$를 알아봅시다. $u$가 0이 아닌 해를 가질 임계조건이 곧 임계점을 의미하므로, 임계점도 구할 수 있습니다. 2절에서 얻은 방정식에 따라 $u$는 다음 식을 만족시켜야 합니다.

\[e^{-u} = h(e^{-u}) = \sum_k \frac{(k+1)p_{k+1}}{\langle k \rangle}e^{-ku} = e^{u}\sum_k \frac{kp_{k}}{\langle k \rangle}e^{-ku}\]

$e^{-ku}=\sum_n \frac{(-u)^n}{n!}k^n$임을 이용하면

\[e^{-u} = e^u\sum_{n=0}^\infty \frac{(-u)^n}{n!} \frac{\langle k^{n+1} \rangle}{\langle k \rangle}\]

다만 $p_k \sim k^{-\gamma}$를 그대로 적용한다면 위 급수의 고차항들($\langle k^{n+1} \rangle$ 부분)은 $n$이 $\lfloor \gamma -2 \rfloor$ 이상일 때 발산하여 일반적인 테일러 전개가 불가능합니다. 이를 해결하기 위해 급수를 적분으로 근사하면 $\sum k^{-s}e^{-ku} \approx \text{Li}_{s}(e^{-u})$ 형태(여기서 $\gamma = s - 1$)가 되는데, 수학적으로 $u \to 0$ 극한에서 다음과 같이 해석적 부분과 비해석적 부분의 합으로 전개됨이 알려져 있습니다.

\[\sum_{k=1}^{\infty} e^{-ku} k^{-s} \approx \underbrace{\sum_{n=0} \frac{(-1)^n}{n!} \zeta(s-n) u^n}_{\text{Analytic}} + \underbrace{\Gamma(1-s) u^{s-1}}_{\text{Non-analytic}}\]

이 전개식을 이용하면 발산하는 모멘트 항 대신 유한한 값을 가지는 비해석적 항인 $\Gamma(1-(\gamma-1))u^{(\gamma-1)-1} = \Gamma(2-\gamma)u^{\gamma-2}$ 항을 얻을 수 있습니다. 따라서 이를 적용하여 방정식을 다시 쓰면 적당한 $\alpha$에 대해 다음과 같습니다.

\[1 = e^{2u} \left[\sum_{n=0}^{\lfloor \gamma - 2 \rfloor} \frac{(-u)^n}{n!} \frac{\langle k^{n+1} \rangle}{\langle k \rangle} + u^{\gamma - 2} \frac{\alpha \Gamma(2-\gamma)}{\langle k \rangle}\right]\] \[1=(1+2u+2u^2+\cdots)\left[1-u \frac{\langle k^{2} \rangle}{\langle k \rangle} + \frac{u^2}{2} \frac{\langle k^{3} \rangle}{\langle k \rangle} + \cdots + u^{\gamma - 2} \frac{\alpha \Gamma(2-\gamma)}{\langle k \rangle}\right]\] \[\left(\frac{\langle k^{2} \rangle}{\langle k \rangle} - 2\right) u - \frac{1}{2} \frac{\langle k(k-2)^2 \rangle}{\langle k \rangle}u^2 + \cdots - u^{\gamma - 2} \frac{\alpha \Gamma(2-\gamma)}{\langle k \rangle} = 0\]

$\gamma$의 값과 관계 없이 $u$ 다음으로 우세한 항은 부호가 같기 때문에, $u$가 0이 아닌 해를 가지기 위해서는 다음 조건을 만족해야 합니다.

\[\Delta := \frac{\langle k^{2} \rangle}{\langle k \rangle} - 2 > 0\]

이전 글에서 첫 번째 이웃의 기댓값과 두 번째 이웃의 기댓값 비율을 통해 얻은 임계점 조건과 일치함을 확인할 수 있습니다.

$\gamma>4$인 경우에는 $u$에 비례하는 항 다음 차수 항이 $u^2$에 비례하는 항이 됩니다. 이 경우 $u$의 해는 대략 다음에 비례하게 됩니다.

\[u \sim \begin{cases} \Delta & \Delta > 0 \\[5pt] 0 & \Delta < 0 \end{cases}\]

$3 < \gamma < 4$에서는 다음과 같이 됩니다.

\[u \sim \begin{cases}\Delta^{\frac{1}{\gamma-3}} & \Delta > 0 \\[5pt] 0 & \Delta < 0 \end{cases}\]

즉 $\gamma=3$을 경계로 임계점 근처에서 GCC 크기의 $\Delta$ 임계지수가 달라짐을 확인할 수 있습니다.

4 Outro

이번 글에서는 차수가 power law distribution을 따르는 scale-free 네트워크에서 상전히 현상과 임계점 근처의 행동을 살펴보았습니다. 특히 branching process approach와 생성함수 방법을 이용하였는데요, 식의 전개과정을 보면 알 수 있지만 반드시 power law distribution을 따르지 않아도 적용 가능한, 굉장히 강력한 방법임을 알 수 있습니다. 생성함수를 이용함으로써 얻을 수 있는 이점은 이뿐만이 아닌데요, 대표적인 예시로 작은 연결요소의 평균 크기 구하기가 있습니다. $\mathcal{P}(z)$의 정의를 이용하면 다음을 얻습니다.

\[\mathcal{P}'(z) = \sum_s P(s) s z^{s-1} \quad \rightarrow \quad \mathcal{P}'(1) = \sum_s sP(s) = \langle s \rangle\]

즉, 작은 연결요소의 평균 크기를 생성함수로부터 쉽게 얻을 수 있습니다. $\mathcal{P}(z)$와 $\mathcal{R}(z)$의 관계를 이용하면 아래와 같이 $\mathcal{P}’(1)$과 $\mathcal{R}’(1)$ 사이의 관계를 알 수 있고, $\mathcal{R}’(1)$은 다시 $\mathcal{R}(z)$를 $h(\omega)$가 연관된 방정식을 풂으로써 얻을 수 있습니다.

\[\mathcal{P}'(1) = g(\mathcal{R}(1)) + g'(\mathcal{R}(1)) \mathcal{R}'(1)\] \[\mathcal{R}'(1) = h(\mathcal{R}(1)) + h'(\mathcal{R}(1)) \mathcal{R}'(1)\]

여기에 다시 $\mathcal{R}(1)=e^{-u}$ 꼴을 넣고 전개를 하면 $\mathcal{P}’(1)$을 얻을 수 있고, 이전 글과 비슷하게 임계점 근처에서 발산하는 현상을 관찰할 수 있을 뿐만 아니라 구체적으로 $\Delta$의 어떤 지수로 발산하는지도 구할 수 있게 됩니다.

References

KIAS-SNU Physics Winter Camp 2025 - Phase Transitions in Networks

M. Newman, Networks, (Oxford university press, 2018)