Perfect Elimination Ordering in Chordal Graph
개요
Chordal Graph
Chordal Graph란, 길이 4 이상의 모든 simple cycle이 chord를 포함하는 그래프를 말한다. 여기서 chord란 cycle에 포함되는 edge는 아니지만 cycle에 포함하는 두 vertex를 잇는 edge를 뜻한다. 즉, 어떤 4개 이상의 vertex를 고르더라도 그 vertex들로 이뤄진 induced subgraph가 simple cycle이 되지 않는 그래프이다. 두 겹치는 구간을 edge로 연결한 Interval graph가 Chordal graph의 한 예이다.
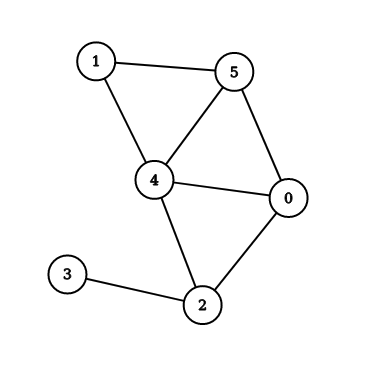
위는 chordal graph의 예이다. 임의의 길이 4 이상인 cycle이 chord를 포함함을 쉽게 알 수 있다.
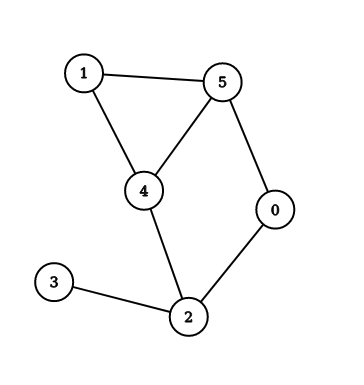
위는 chordal graph가 아닌 그래프의 예이다. vertex 0, 2, 4, 5로 이루어지는 cycle이 chord를 포함하지 않는다.
Perfect Elimination Ordering
그래프 $G = (V, E)$의 ordering $X$가 모든 vertex $v$에 대해, $v$와 인접한 정점들 중 $X$에서 $v$보다 늦게 등장하는 정점들이 clique(완전그래프)를 이루는 ordering이라면 $X$를 $G$의 perfect elimination ordering이라고 한다. 그래프 $G$에 chord를 가지지 않는 길이 4 이상의 cycle이 존재한다면 cycle에 포함되는 vertex 중 처음으로 등장하는 vertex는 perfect elimination ordering의 조건을 만족할 수 없으므로 는 perfect elimination ordering이 존재하지 않는다. 또한, 모든 chordal graph에 대해 perfect elimination ordering이 존재함이 알려져 있다(perfect elimination ordering을 직접 찾는 방법을 이후에 알아볼 것이다). 즉, 그래프 $G$의 perfect elimination ordering이 존재함과 $G$가 chordal graph임은 동치이다.

앞서 본 chordal graph의 perfect elimination ordering을 구해보자. 2와 인접한 vertex인 3, 0, 4는 clique을 이루지 않으므로 2로 시작하지는 않는다는 사실을 알 수 있다. 맨 앞에 올 수 있는 vertex를 그래프에서 제거하면서 나열하면 된다. 처음에는 3 또는 1이 올 수 있다. 이와 같은 방식으로 찾으면 3, 2, 0, 5, 4, 1이 perfect elimination ordering 중 하나임을 알 수 있다.
Finding a perfect elimination ordering in a chordal graph
suboptimal algorithms
$G = (V, E)$의 perfect elimination ordering은 앞에서부터 순서대로 간단하게 구할 수 있다. 어떤 vertex $v$가 존재하여 $v$와 인접한 vertex들이 clique을 이루면 $v$를 ordering의 맨 뒤에 추가하고, $G$에서는 제거하는 과정을 반복하면 perfect elimination ordering이 나온다. 만약 모든 vertex가 제거되지 않았는데 조건을 만족하는 vertex $v$를 찾을 수 없다면 perfect elimination ordering이 없는 것이므로 chordal graph가 아니라는 사실 역시 판정할 수 있다. 이를 naive한 방법으로 구현하면 $O(V^4)$의 매우 느린 시간복잡도를 갖는 알고리즘이 된다. 이를 개선한 방법으로 다음과 같은 알고리즘을 생각할 수 있다. 각 vertex $v$에 대해 아직 제거되지 않은 vertex들 중 $v$와 인접한 vertex들의 집합을 $N(v)$, 내에서 서로 연결되지 않은 vertex 쌍의 개수를 $C(v)$라고 할 때 $C(v)$가 0이 되는 정점 을 queue에 넣고, queue의 head에 있는 정점을 제거하는 방식으로 perfect elimination ordering을 구할 수 있다. 정점 $v$를 제거할 때 $v$와 인접한 정점들의 $C(v)$ 값을 업데이트해주어야 한다. 자세한 알고리즘을 실제 코드로 표현하면 다음과 같다.
#include<cstdio>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
using namespace std;
const int N_ = 101000;
int n, m, C[N_], head, tail, vis[N_];
set<int>graph[N_];
queue<int>Q;
vector<int>Order;
map<int, int>Edge[N_];
int main() {
int i, j, k;
scanf("%d%d", &n, &m);
for (i = 0; i < m; i++) {
int a, b;
scanf("%d%d", &a, &b);
graph[a].insert(b);
graph[b].insert(a);
Edge[a][b] = Edge[b][a] = 1;
}
for (i = 1; i <= n; i++) {
int sz = graph[i].size();
C[i] = sz * (sz - 1) / 2; // C[i]는 i와 인접한 정점들 중 서로 인접하지 않은 정점 쌍의 개수
vector<int>neighbor;
for (auto &x : graph[i])neighbor.push_back(x);
for (j = 0; j < neighbor.size(); j++) {
for (k = j + 1; k < neighbor.size(); k++) {
if (Edge[neighbor[j]].count(neighbor[k]))C[i]--; // C[i]는 i와 인접한 정점 쌍 전체에서 i를 포함하는 3-cycle의 개수를 빼서 구할 수 있다.
}
}
}
for (i = 1; i <= n; i++) {
if (!C[i]) {
Q.push(i); //C[i]가 0이면 i를 큐에 넣는다.
vis[i] = 1;
}
}
while (!Q.empty()) {
int v = Q.front();
Order.push_back(v);
Q.pop();//큐의 head에 있는 정점 v를 ordering에 추가하고, 그래프에서 제거한다.
int sz = graph[v].size();
for (auto &w : graph[v]) {
graph[w].erase(v); //v와 인접한 정점 w에 대해 간선 (v,w)를 제거
C[w] += -graph[w].size() + (sz - 1); // w와 인접한 정점 중 v와 인접한 것은 |N(v)|-1개이므로 인접하지 않은 것은 |N(w)| - (|N(v)|-1)개이고, v를 제거했을 때 C[w]는 이 값만큼 감소한다.
if (!C[w] && !vis[w]) { //C[w]가 0이 되면 큐에 추가한다.
vis[w] = 1;
Q.push(w);
}
}
}
if (Order.size() != n) {
puts("0");
}
else {
printf("1\n");
for (auto &v : Order)printf("%d ", v);
}
}
위 알고리즘에서 처음에 $C$ 배열을 초기화하는 부분을 제외하면 시간복잡도는 set을 $O(E)$번 접근하는 것이 결정하므로 $O(E log E)$의 시간복잡도를 가진다. 그러나 $C$ 배열 초기화에서 $O(VE)$ 시간이 걸릴 수 있기 때문에 충분히 빠르지 못하다. $C$ 배열 초기화는 모든 3-cycle을 구하면 쉬운데, 3-cycle의 개수는 $O(E \sqrt E)$개임이 알려져 있고, 또한 $O(E \sqrt E)$ 시간에 모든 3-cycle을 구하는 방법이 존재한다. 아이디어는 모든 edge $(u, v)$에 대해 $min(degree(u), degree(v))$의 총 합이 $O(E \sqrt E)$임을 이용하는 것이다. C배열을 초기화하는 부분의 코드는 아래와 같다.
for (i = 0; i < m; i++) {
int a, b;
scanf("%d%d", &a, &b);
graph[a].insert(b);
graph[b].insert(a);
adj[a].push_back(b);
adj[b].push_back(a);
Edge[a][b] = Edge[b][a] = 1;
}
for (i = 1; i <= n; i++) {
if (!adj[i].empty()) {
sort(adj[i].begin(), adj[i].end());
}
int sz = adj[i].size();
C[i] = sz * (sz - 1) / 2;
}
for (i = 1; i <= n; i++) {
for (auto &x : adj[i])IsNeighbor[x] = 1;
for (auto &x : adj[i]) {
if (adj[x].size() < adj[i].size() || (adj[x].size() == adj[i].size() && x < i)) {
for (auto &y : adj[x]) {
if (IsNeighbor[y])C[y]--;
}
}
}
for (auto &x : adj[i])IsNeighbor[x] = 0;
}
$C$ 배열을 위와 같이 초기화하면 전체 시간복잡도 $O(E \sqrt E)$에 perfect elimination ordering을 구할 수 있다.
Lexicographic breadth-first search
Lexicographic breadth-first search는 일반적인 breadth-first search와 거의 비슷한데, queue에서 빠지는 vertex를 어떻게 결정하는지가 조금 다르다. vertex $v$에 대해 $v$와 인접한 vertex 중 이미 방문한 vertex(queue에서 빠진 vertex)들의 방문순서를 정렬한 sequence를 $P(v)$라 하자. Lexicographic breadth-first search에서는 queue에 있는 vertex들 중 $P(v)$가 Lexicographically minimum인 vertex를 가장 먼저 방문한다(queue에서 제거한다). 일반적인 BFS와 비교하면 일반적인 BFS는 $P(v)$의 첫번째 원소가 minimum인 vertex를 방문하는데, Lexicographic BFS는 $P(v)$ 전체를 비교한다는 차이가 있다.
Lexicographic breadth-first search는 선형 시간에 구현할 수 있음이 알려져 있다. 의사 코드는 아래와 같이 나타낼 수 있다.
- 집합들의 list $\Sigma$를 초기화한다. 처음에 $\Sigma$는 모든 vertex를 포함하는 집합 하나로 이루어진다.
- output sequence를 empty sequence로 초기화한다.
- While $\Sigma$ is non-empty:
- $\Sigma$의 첫 번째 집합이 비어있지 않은 경우, 그 집합에서 vertex $v$를 고른다.
- 비어있는 경우, 첫 번째 집합을 지우고 비어있지 않은 집합이 나올때까지 반복하여 vertex $v$를 고른다.
- $v$를 output sequence의 맨 뒤에 추가한다.
- $v$와 연결된 모든 edge $(v, w)$ 중 $w$가 아직 output sequence에 추가되지 않은 edge들에 대해:
- $w$가 집합 $S$의 원소라고 하자.
- 만약 $S$가 현재 loop ($v$에 관한 처리)에서 변경되지 않은 집합이라면, $\Sigma$에서 $S$ 앞에 새로운 비어있는 집합 $T$를 추가한다. $S$가 변경된 적이 있다면, $S$ 이전의 집합을 $T$라고 하자.
- $w$를 $S$에서 $T$로 옮긴다.
Lexicographic breadth-first search를 하고 나면 chordal graph 판별과 perfect elimination ordering 찾기는 매우 쉬워진다. Lexicographic breadth-first search의 방문 순서를 lexicographic ordering이라 하자. 각 vertex $v$에 대해, $v$와 인접한 vertex들 중 lexicographic ordering에서 $v$보다 앞에 오는 것들의 집합을 earlier neighbor of $v$라 하자.
earlier neighbor가 공집합이 아닌 각 vertex $v$에 대해, $v$의 earlier neighbor 중 가장 나중 순서인 neighbor를 $w$라 하자. 만약 $v$의 earlier neighbor 중 $w$의 earlier neighbor도 아니고 $w$ 자신도 아닌 것이 존재한다면, 그래프는 chordal graph가 아니다. 그런 경우가 존재하지 않는다면 chordal graph이며, lexicographic ordering의 reverse sequence가 perfect elimination ordering이 된다.
Lexicographic BFS는 선형 시간에 구현할 수 있다. 아래는 이를 List를 이용하여 실제로 구현한 코드이다. (iterator를 주의깊게 handle해야 한다.)
#include<cstdio>
#include<algorithm>
#include<set>
#include<queue>
#include<vector>
#include<map>
#include<list>
#include<unordered_map>
using namespace std;
const int N_ = 101000;
int n, m, vis[N_], Res[N_], ord[N_];
vector<int>graph[N_];
struct Set {
list<int>L;
int last;
}; // 각 집합에 대해 원소를 리스트에 저장하고, 또한 현재 step에서 이미 빠져나간 원소가 있는 set인지 체크하기 위해 last 변수도 저장한다.
list<Set> w; //w는 Set들의 리스트이다.
list<Set>::iterator Where[N_]; //Where[v]는 v가 있는 Set의 위치를 들고 있다.
list<int>::iterator Addr[N_]; //Addr[v]는 v가 있는 Set의 list에서 실제로 v가 어느 위치에 있는지를 들고 있다.
unordered_map<int, int>Edge[N_]; //Edge[u][v]는 u와 v가 인접한 vertex인 경우에만 1이다.
typedef list<int>::iterator lit;
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++) {
int a, b;
scanf("%d%d", &a, &b);
graph[a].push_back(b);
graph[b].push_back(a);
Edge[a][b] = Edge[b][a] = 1;
}
int i;
list<int>TP;
for (i = 1; i <= n; i++)TP.push_back(i);
w.push_back({ TP,0 });
for (i = 1; i <= n; i++)Where[i] = w.begin();
for (lit t = w.front().L.begin(); t != w.front().L.end(); t++) {
Addr[*t] = t;
}
int cnt = 0;
while (!w.empty()) {
auto cur = w.begin(); // 첫 집합 cur
if (cur->L.empty()) {
w.erase(w.begin());
continue;
}
cnt++;
int v = cur->L.front(); //cur의 원소 v를 선택하여 ordering에 추가하고, Set에서 제거한다.
Res[cnt] = v;
ord[v] = cnt;
vis[v] = 1;
cur->L.pop_front();
for (auto &u : graph[v]) {
if (vis[u])continue;
if (Where[u]->last != cnt) { //만약 u가 들어있는 set이 현재 v에 대한 step에서 방문하지 않은 set인 경우
auto it = Where[u];
list<int>new_list;
new_list.push_back(u);
w.insert(it, { new_list, 0 });
Where[u]->L.erase(Addr[u]);
Where[u]->last = cnt;
Where[u]--;
Addr[u] = Where[u]->L.begin();
}
else { //만약 u가 들어있는 set이 현재 v에 대한 step에서 방문했던 set인 경우
auto it = Where[u];
Where[u]->L.erase(Addr[u]);
Where[u]--;
Where[u]->L.push_back(u);
Addr[u] = Where[u]->L.end();
Addr[u]--;
}
}
}
for (int v = 1; v <= n; v++) {
int Max = -1;
for (auto &u : graph[v]) {
if (ord[u] < ord[v])Max = max(Max, ord[u]);
}
if (Max == -1)continue;
int pv = Res[Max]; //v와 인접한 vertex 중 lexicographical BFS에서 방문 순서가 v보다 빠른 것들 중 가장 느린 vertex
for (auto &u : graph[v]) {
if (u != pv && ord[u] < ord[v] && !Edge[pv].count(u)) {
puts("0"); // Perfect elimination ordering이 존재하지 않는 경우
return 0;
}
}
}
for (i = 1; i <= n; i++)printf("%d ", Res[i]);
}
코드가 짧지 않지만, set을 이용하는 $O(E log V)$ 의 간단한 구현도 존재한다.
문제 풀이
Maximal clique in chordal graph
maximal clique의 개수는 일반적인 그래프에서는 exponential하게 증가하지만, chordal graph에서는 linear하다. perfect elimination ordering 순서대로 보면 연결된 모든 vertex가 clique를 이뤄야 하므로 maximal clique, maximum clique을 구하는 것은 매우 간단하다. $v$의 neighbor 중 PEO에서 $v$보다 늦게 오는 것의 개수를 $N_v$라 하면 $max(N_i) + 1$이 maximum clique의 크기가 된다.
Graph coloring in chordal graph
인접한 두 vertex의 색이 다르도록 하는 coloring의 최소 색깔 수를 그래프의 chromatic number라 한다. chordal graph에서 chromatic number는 maximum clique의 정점 수와 같으므로, linear time에 구할 수 있다. 나아가, 그래프에서 색깔이 $x$개 일 때 가능한 coloring의 수를 다항식으로 나타낸 것인chromatic polynomial 역시 구할 수 있다. $(x-N_1)(x-N_2)…(x-N_n)$이 chordal graph에서의 chromatic polynomial이 된다.
Kakao Code Festival 2018 G. 자석 장난감
이 문제는 perfect elimination ordering을 구하는 문제이다. 앞서 소개한 linear한 시간복잡도의 구현 뿐 아니라 $O(E log V)$, $O(E \sqrt E)$의 구현 모두 시간 안에 통과한다.
ACM-ICPC Seoul Regional Contest 2018 I. Square Root
그래프가 주어질 때, 이것이 어떤 tree에서 거리가 2 이하인 vertex를 edge로 연결한 graph인지 아닌지 판정하고, 만약 그렇다면 원래 tree로 가능한 tree를 찾는 문제이다. (이를 original tree라고 하자) tree에서 거리가 2 이하인 vertex를 edge로 연결한 그래프에서는 길이 4 이상인 모든 cycle에 대해 chord가 존재함을 쉽게 보일 수 있으므로, Chordal graph가 아니면 해가 없음을 쉽게 판단할 수 있다. Chordal graph인 경우, perfect elimination ordering을 거꾸로 한 ordering이 $v_1$, $v_2$, .., $v_n$이라 하자. 즉, $v_n$, $v_{n-1}$, …, $v_1$이 perfect elimination ordering이라 하자.
만약 주어진 그래프가 완전그래프라면 1과 다른 모든 vertex를 이은 tree가 답이 된다. 그렇지 않다면 $v_1$, $v_2$, …, $v_k$가 완전그래프가 아닌 가장 작은 k가 존재한다. 그러면 original tree에서 $v_1$, …, $v_{k-1}$은 중심 vertex가 하나 있고 나머지 vertex들은 중심 vertex에 연결되어있는 형태가 되어야 한다. 또한 $v_k$는 주어진 그래프에서 정확히 두 vertex와 연결되어야 하고, 두 vertex 중 하나는 중심 vertex, 다른 하나는 실제로 $v_k$와 original tree에서 연결되어 있는 vertex여야 한다.
이를 이용하면 원래 tree에서 $v_1$, …, $v_k$로 induced되는 subgraph로 가능한 것이 두 가지 밖에 없음을 관찰할 수 있다. 둘 중 하나로 모양을 정해놓은 후 $v_{k+1}$, …, $v_n$을 붙이는 것은 간단하게 해결할 수 있다.
자세한 코드는 아래와 같다.
#include<cstdio>
#include<algorithm>
#include<set>
#include<queue>
#include<vector>
#include<map>
#include<list>
#include<unordered_map>
using namespace std;
const int N_ = 101000;
int n, m, vis[N_], Res[N_], ord[N_], st;
vector<int>graph[N_], G[N_];
struct Set {
list<int>L;
int last;
};
list<Set> w;
list<int>::iterator Addr[N_];
list<Set>::iterator Where[N_];
unordered_map<int, int>Edge[N_], Tree[N_];
typedef list<int>::iterator lit;
void Add_Edge(int a, int b) {
G[a].push_back(b);
G[b].push_back(a);
Tree[a][b] = Tree[b][a] = 1;
}
bool Solve() {
int i, j;
for (i = st; i <= n; i++) {
int x = Res[i];
vector<int>T;
for (auto &y : graph[x]) {
if (ord[x] > ord[y]) {
T.push_back(y);
}
}
int r1 = -1, r2 = -1;
for (j = 1; j < T.size(); j++) {
if (Tree[T[j]][T[0]]) {
r1 = T[0], r2 = T[j];
break;
}
}
if (G[r1].size() + 1 != T.size())r1 = -1;
if (G[r2].size() + 1 != T.size())r2 = -1;
for (auto &t : T) {
if (r1 == -1 || r2 == -1)break;
if (t!=r1 && !Tree[t][r1]){
r1 = -1;
}
if (t!=r2 && !Tree[t][r2]) {
r2 = -1;
}
}
if (r1 == -1)r1 = r2;
if (r1 == -1) {
return false;
}
Add_Edge(r1, x);
}
printf("%d\n%d\n", 1, n);
for (i = 1; i <= n; i++) {
for (auto &x : G[i]) {
if (x < i) {
printf("%d %d\n", x, i);
}
}
}
return true;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++) {
int a, b;
scanf("%d%d", &a, &b);
graph[a].push_back(b);
graph[b].push_back(a);
Edge[a][b] = Edge[b][a] = 1;
}
int i;
list<int>TP;
for (i = 1; i <= n; i++)TP.push_back(i);
w.push_back({ TP,0 });
for (i = 1; i <= n; i++)Where[i] = w.begin();
for (lit t = w.front().L.begin(); t != w.front().L.end(); t++) {
Addr[*t] = t;
}
int cnt = 0;
while (!w.empty()) {
auto cur = w.begin();
if (cur->L.empty()) {
w.erase(w.begin());
continue;
}
cnt++;
int v = cur->L.front();
Res[cnt] = v;
ord[v] = cnt;
vis[v] = 1;
cur->L.pop_front();
for (auto &u : graph[v]) {
if (vis[u])continue;
if (Where[u]->last != cnt) {
auto it = Where[u];
list<int>new_list;
new_list.push_back(u);
w.insert(it, { new_list, 0 });
Where[u]->L.erase(Addr[u]);
Where[u]->last = cnt;
Where[u]--;
Addr[u] = Where[u]->L.begin();
}
else {
auto it = Where[u];
Where[u]->L.erase(Addr[u]);
Where[u]--;
Where[u]->L.push_back(u);
Addr[u] = Where[u]->L.end();
Addr[u]--;
}
}
}
for (int v = 1; v <= n; v++) {
int Max = -1;
for (auto &u : graph[v]) {
if (ord[u] < ord[v])Max = max(Max, ord[u]);
}
if (Max == -1)continue;
int pv = Res[Max];
for (auto &u : graph[v]) {
if (u != pv && ord[u] < ord[v] && !Edge[pv].count(u)) {
puts("-1");
return 0;
}
}
}
vector<int>T1, T2;
int m1, m2, ch;
int ss = 0;
for (i = 1; i <= n; i++) {
int x = Res[i];
for (auto &y : graph[x]) {
if (ord[x] > ord[y])ss++;
}
if (ss != i * (i - 1) / 2) {
vector<int>T;
for (auto &y : graph[x]) {
if (ord[x] > ord[y])T.push_back(y);
}
if (T.size() != 2) {
puts("-1");
return 0;
}
m1 = T[0];
m2 = T[1];
for (int j = 1; j < i; j++) {
if (Res[j] != m1)T1.push_back(Res[j]);
if (Res[j] != m2)T2.push_back(Res[j]);
}
ch = x;
st = i + 1;
break;
}
}
if (i == n + 1) {
printf("1\n%d\n",n);
for (i = 1; i < n; i++) {
printf("%d %d\n", i, n);
}
return 0;
}
for (auto &t : T1)Add_Edge(m1, t);
Add_Edge(m2, ch);
if (Solve())return 0;
for (i = 1; i <= n; i++) {
G[i].clear();
Tree[i].clear();
}
for (auto &t : T2)Add_Edge(m2, t);
Add_Edge(m1, ch);
if (Solve())return 0;
puts("-1");
}
결론
Chordal graph는 interval graph 등 많은 graph class들을 포함하는 class이며, 문제 풀이에서 나오는 많은 종류의 그래프가 chordal graph 형태를 가집니다. Chordal graph에서는 여러 어려운 문제들을 쉽게 해결할 수 있는데, perfect elimination ordering을 통해 그 대부분의 풀이를 찾을 수 있습니다. 그래프 문제가 아닌 문제들도 그래프로 변형시켜 chordal graph로 만든 후 생각하는 접근도 문제 해결에 도움이 될 수 있습니다.