Manacher's Algorithm
목차
개요
이 포스트를 쓰며
학기가 시작되어 모든 알고리즘들을 한번씩 보면서 넘어가던 도중 사람들이 잘 관심 가지지 않지만, 알아두면 재미있을법한 알고리즘인 Manacher’s Algorithm 을 소개해보고자 한다. Manacher’s Algorithm은 String 내에 존재하는 모든 Palindrome을 $O(N)$에 구하는 강력한 알고리즘이다. 물론 이 알고리즘이 실전에 출제되는 경우는 매우 드물지만 원리 자체가 재미있고 시간복잡도가 $O(N)$이 되는 원리가 재미있는 알고리즘이므로 자세하게 설명해보고자 한다.
팰린드롬
팰린드롬을 모르는 사람을 위해 간단히 설명하자면 앞에서 읽으나 뒤에서 읽으나 항상 똑같이 읽어지는 문자열을 의미한다. 예를 들어, “여보안경안보여” 는 팰린드롬이다. 거꾸로 읽으나 제대로 읽으나 “여보안경안보여”이다. 물론, 한국어로 문제를 내는 경향은 드무니, 알파벳 기준으로 설명한다면, “ababa”등이 있을 것이다. 이러한 거꾸로 읽으나 제대로 읽으나 항상 같은 문자열을 팰린드롬이라 하며, 더 엄밀한 정의로는 문자열의 길이를 $n$이라고 하고 $0$ 부터 $n-1$까지 각 문자열에 해당하는 문자에 번호를 매긴다면, (이를테면 “branch” 에서 0번째는 ‘b’ 고 4번째는 ‘c’가 된다), $i$번째 문자 와 $n-i-1$ 번째 문자가 같은 문자열을 의미한다.
간단한 원리
우선 간단한 반복문, 배열만 사용할 줄 알면 되는 매우 간단하고 이해하기도 쉬운 알고리즘이다. 단, 다이나믹 프로그래밍에 대한 약간의 지식이 있으면 도움 이 될것이다. 일단 부분 문자열(주어진 문자열에서 연속되는 맨 앞에서 부터 $k$개, 뒤에서 부터 $l$개($k + l < n$)를 자른 문자열)중에 팰린 드롬이 되는 제일 긴 문자열을 찾고, 그 문자열의 중심으로 부터 대칭되는 부분 문자열 역시 팰린드롬이다 라는 아이디어에서 출발하는 알고리즘이다. 그리고 그것을 이용하여 모든 팰린드롬을 구한다.
기본
일단 pseudo code는 다음과 같다.
s = input string
p = [radius of palindrome]
r = -1 # end of palindrome
c = -1 # center of palindrome
for i in range(0, n - 1)
if r >= i
p[i] = min(r - i, p[c * 2 - i]) # c + (c - i) symmetric point
else
p[i] = 0
while i + p[i] + 1 < n
if s[i + p[i] + 1] == s[i - p[i] - 1]
p[i] += 1
else
break
if i + p[i] > r
r = i + p[i]
c = i
$s$는 입력으로 주어지는 문자열을 의미한다. $p$는 배열으로서 현재위치에서의 팰린드롬의 반경을 의미한다. 즉 “abcba” 가 있다고 한다면 $c$에 해당하는 반경은 $2$가 된다. 이때, $p[i] * 2 + 1$을 하면 그 팰린드롬에 해당하는 부분 문자열의 최대 길이를 알 수 있다. $r$ 은 위의 기본 원리에서 설명했던 부분 문자열의 끝을 의미한다. $c$는 그 부분문자열의 중앙을 의미한다.
이제 여기서 for 에서 $r$, 즉, 부분 문자열의 끝보다 $i$가 작으면 그 부분문자열에 대칭하는 지점에 해당하는 $p$값을 가져온 뒤, $r - i$, 즉, 끝 지점과 현재 $i$와의 거리를 구해서 둘 중 작은 쪽으로 넣어준다. 이렇게 하는 이유는 대칭되는 지점이 팰린드롬이 해당 부분문자열을 벗어나는 지점에 있다면, 그것이 현재 $i$가 똑같으리라는 보장이 없기 때문이다. 자세한건 그림을 통해 확인해보자.
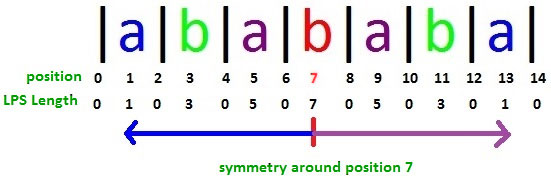
위에 사진에서 “abababa” 에 앞에는 “abab”를 추가로, 뒤에는 “cbcb”를 추가로 넣는다고 해보자. 뒤에 만약을 가정하여, 가장 마지막 문자열의 대칭 지점과 원래 지점에서 는 bab로 인하여 실제로 $p[c * 2 - i]$는 더 길것이다. 하지만 $p[i]$는 절대로 그것보다 길게 나올 수 없다. 이것 때문에 $r - i$와 $p[c * 2 - i]$를 비교하는 것이다.
구현
위의 pseudo code 를 C++로 구현한 코드이다.
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 100001
using namespace std;
int p[MAXN]; // 팰린드롬의 반경
char o[MAXN]; // 문자열
int main() {
int i;
int n; // 문자열의 길이
int r, c; // 맨 끝의 위치, 중간의 위치
r = c = -1;
scanf("%s",o);
n = strlen(o);
// even palindrome
for (i = n - 1; i >= 0; i--) {
o[(i << 1)+1] = o[i];
o[i << 1] = '#';
}
n <<= 1;
o[n++] = '#';
for (i = 0; i < n; i++) {
if (r >= i) p[i] = min(r - i, p[c * 2 - i]); // 작은 쪽을 넣어준다.
else p[i] = 0;
while (i + p[i] + 1 < n && i - p[i] - 1 >= 0 && o[i + p[i] + 1] == o[i - p[i] - 1]) p[i]++; // 같으면 증가
if (i + p[i] > r) { // 끝지점을 넘어서면 그때마다 갱신
r = i + p[i];
c = i;
}
}
for(i=0;i<n;i++) printf("%d ",p[i]);
return 0;
}
먼저 살펴볼 수 있는 것은 even palindrome 으로 주석처리된 부분인데, 이는 짝수 팰린드롬의 처리를 의미한다. 위에서 홀수 팰린드롬만을 설명했었다. 그렇다면 짝수 팰린드롬은 어떻게 처리할까?

위 그림에서 보다 싶이 문자열의 각 $i$번째 문자들을 $2i + 1$번째로 옮긴 뒤, 첫번째와 맨 마지막, 그리고 사이사이 남는 공간에 ‘#’ 문자를 끼워주는 방법이다. 이렇게 하면, linear한 추가 공간과 시간을 사용하여 짝수 팰린드롬 또한 찾을 수 있게 된다.
그렇게 되어서 위 코드에서 ‘#’을 채워주는 것이다. 구현은 이렇게 간단하다.
그렇다면 시간복잡도는 어떻게 $O(N)$이 되는것일까? 그 비밀은 while에 숨겨져있다. 얼핏 보면 $O(N^{2})$ 처럼 보이지만, while은 실제로 linear하게 동작한다. 그 이유는, $p[i]$가 증가하려면 $r$에 변화가 있다는 뜻이다. $r$에 변화가 없다는건, 대칭되는 $p[c * 2 - i]$가 $r$보다 작은 경우여서, $p[i]$가 증가할 이유가 없기 때문이다. 혹은, 정확히 r에 도달할 수 도 있다. 이 경우에도 마찬가지로 대칭되는 지점과 공유하므로 $p[i]$가 증가할 일은 없다. 그런데 $r$은 감소할 일이 없는 변수이다. 즉, 증가하기만 하고 감소할 일은 없으니 while이 도는 횟수는 결국 전체 합쳐서 $n$보다 클수가 없다. 따라서, 시간복잡도는 $O(N)$이 된다. 전에 있던 p를 사용하여 그 다음 p를 결정하는건 약간 다이나믹 프로그래밍과 비슷한 아이디어지만 대칭성을 이용하는 아름다운 알고리즘이 된다.
이제 문제를 풀어보도록 하자.
문제풀이
팰린드롬
이 링크를 통하여 문제를 확인해 볼 수 있다. 너무나 당당하게 팰린드롬이라 적힌 문제이다. 이 문제는 각 문자들을 팰린드롬으로 잘게 쪼갰을 때 그 개수를 최소화 하는 문제이다. 그렇다면 가장 먼저 떠오르는 방법이 무엇일까? 그렇다 바로 DP 이다. 현재 위치를 $i$ 라고 한다면 $table[i]=min(table[j]+1) (j < i)$의 점화식으로 구해내는 것이다. 이때 $[j + 1, i]$구간의 문자열이 팰린드롬인지만 확인하면 되고 $table[j]$가 가능한 숫자인지만 검증하면 된다. 자, 우선 $table[j]$가 가능한 숫자인것을 검증하는 것은 매우 쉬운 일이다. 하지만, 특정 구간의 문자열이 팰린드롬이라는걸 확신하는 방법은? 그렇다 manacher를 이용하면 된다. 아래 코드는 $p$의 범위를 활용하여 $p[i]$에 대해 $table[i+j]$를 $table[i-j]$로 갱신하는 방법을 택했다. 이 경우엔 굳이 검증작업이 필요가 없다.
#include <stdio.h>
#include <string.h>
int n;
int p[4010];
int table[4010];
char o[4010];
void manacher() {
int i;
int c = -1;
int k;
for(i=0;i<n;i++) {
if(c == -1) k = 0;
else k = p[2*c-i] <= c+p[c]-i ? p[2*c-i] : c+p[c]-i; // r을 사용하지 않고 대신 c + p[c]를 활용하였다.
while(i-k-1 >= 0 && i+k+1 < n && o[i-k-1] == o[i+k+1]) k++;
if(i+k > c+p[c]) c = i;
p[i] = k;
}
}
int main() {
int i;
int k1;
scanf("%s",o);
n = strlen(o);
for(i=n-1;i>=0;i--) {
o[i*2+1] = o[i];
o[i*2] = '#';
}
n *= 2;
o[n++] = '#';
manacher();
int j;
for(i=0;i<n;i++) table[i] = 100000000;
table[0] = table[1] = table[2] = 1;
for(i=0;i<n;i++) {
for(j=p[i];j>=0;j--) {
if(i-j == 0) table[i+j] = 1;
k1 = 0x7fffffff;
if(o[i-j] == '#') {
k1 = table[i-j];
if(i-j-1 >= 0 && k1 > table[i-j-1]) k1 = table[i-j-1];
if(k1 + 1 < table[i+j]) table[i+j] = k1 + 1;
}
else {
if(i-j-1 >= 0) k1 = table[i-j-1];
if(i-j-2 >= 0 && k1 > table[i-j-2]) k1 = table[i-j-2];
if(k1 + 1 < table[i+j]) table[i+j] = k1 + 1;
}
}
}
printf("%d",table[n-1]);
return 0;
}
Casting Spells
이 링크를 통하여 문제를 확인할 수 있다. 이 문제는 주문을 외우는 데 주문에는 각각의 힘이 있다고 한다. 그 힘이란 어떤 임의의 문자열 $w$가 있다고 가정했을 때, $ww^{R}ww^{R}$이 입력으로 주어지는 문자열 내부에 존재한다고 하자. 이때 $ww^{R}ww^{R}$ 의 길이가 제일 긴 것이 그 주문의 힘이라고 한다. ($w^{R}$은 뒤집기)
이 문제는 바로 눈치챘겠지만, 짝수 팰린드롬 두개를 이어붙여서 또 팰린드롬이 나오는지 확인하는 문제이다. 그렇다면 짝수 팰린드롬 두개를 이어붙여서 제일 긴 팰린드롬을 찾는건 어떻게 할까? 그것은 간단하다. plane sweep 아이디어를 이용하는 것이다. 우선 $ww^{R}ww^{R}$ 을 찾고 $ww^{R}$ 가 되어줄 다른 팰린드롬이 있는지 $i$ 를 늘려나가면서 찾는 것이다. 먼저 $i$를 $set$에 집어넣고, $i + p[i]$ 지점에 그 $i$를 다시 지우는 것이다. 그런식으로 넣고 지워가면서 어떤 지점 $i$에 대해서 $\frac{i - p[i]}{2}$ 의 lower bound 를 찾고 그 지점에 해당하는 i가 존재하는지 찾으면 되는것이다. 이때의 시간복잡도는 $O(N log N)$ 이 된다.
아래는 위 풀이를 구현한 코드이다.
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <set>
using namespace std;
int p[600010];
char o[600010];
set<int> st;
vector<int> right[600010];
int main() {
int z;
scanf("%d", &z);
while(z--) {
int n;
scanf("%s", o);
n = (int)strlen(o);
for(int i = n - 1; i >= 0; i--) {
o[i * 2 + 1] = o[i];
o[i * 2] = '#';
}
o[n * 2] = '#';
n = n * 2 + 1;
o[n] = '\0';
int r;
int c = r = -1;
for(int i = 0; i < n; i++) { // 일단 manacher로 반경을 모두 구해놓고 시작한다.
if(r >= i) p[i] = min(p[c * 2 - i], r - i);
else p[i] = 0;
while(i + p[i] + 1 < n && i - p[i] - 1 >= 0 && o[i + p[i] + 1] == o[i - p[i] - 1]) p[i]++;
if(i + p[i] > r) {
r = i + p[i];
c = i;
}
}
for(int i = 0; i < n; i += 2) {
right[i].push_back(i + 1); // 현재 지점
right[i + p[i]].push_back(-i - 1); // 길이의 한계, 즉 삭제되는 시점
}
int ans = 0;
for(int i = 0; i < n; i += 2) {
// 발견되는 시점으로 set에 넣어준다.
for(int j = 0; j < right[i].size(); j++) if(right[i][j] > 0) st.insert(right[i][j] - 1);
//해당 길이를 포함하는 짝수 팰린드롬이 존재하는지, 그것도 가장 긴것으로 찾는다.
set<int>::iterator it = st.lower_bound(i - p[i] / 2);
if(it != st.end() && st.size()) {
ans = max(ans, (i - *it) * 2);
}
// 삭제되는 시점이므로 삭제해준다.
for(int j = 0; j < right[i].size(); j++) if(right[i][j] < 0) st.erase(-right[i][j] - 1);
}
st.clear();
printf("%d\n",ans);
for(int i = 0; i < n; i++) {
p[i] = 0;
right[i].clear();
}
}
return 0;
}
Sonya and Matrix Beauty
이 링크를 통하여 문제를 확인할 수 있다. 이 문제는 $n \times m$ 행렬에서 한 행에 들어있는 문자들을 모두 재배열 할 수 있을때(이러한 작업을 모든 행에서 수행 가능)재배열 하고 난뒤, $i_{1}, j_{1}, i_{2}, j_{2}$ 네 좌표로 만들 수 있는 사각형에서 모든 행과 열이 팰린드롬이 되는지 확인하는 문제이다. 그리고 그러한 네 좌표들의 모든 경우의 수를 출력하는 문제이다.
일단, 가장 먼저 DP를 사용하여 알파벳 성분들을 모두 구해서 행이 고정 되었을때, $j_{1}, j_{2}$의 알파벳 성분들을 26개로 구해서 하나의 거대한 알파벳이라고 생각하는 것이다. 그러면 하나의 거대한 문자열이 만들어지는것을 확인 할 수 있다. 여기서 더 나아가서 26개의 성분들이 전부 짝수이거나, 혹은 단 한개만 홀수이고 나머지는 짝수인경우 행에 대해서 팰린드롬을 만들 수 있다는 사실도 알 수 있다.
즉, 열, $j_{1}, j_{2}$ 을 고정해 놓고 그것을 거대한 문자열이라고 보고 manacher를 실행하는 문제로 바뀌게 된다! 따라서 이 경우에 시간복잡도는 $O(nm^{2})$ 이다.
아래는 위 풀이를 구현한 코드이다.
#include <cstdio>
#include <algorithm>
using namespace std;
char o[520][520];
int cnt[520][31];
int impossible[520];
int tr[128];
int p[520];
bool equal(int x, int y) { // 두 성분을 비교
if(impossible[x] || impossible[y]) return false; //불가능 할때는 무조건 거짓을 반환
for(int i = 0; i < 27; i++) {
if(cnt[x][i] != cnt[y][i]) return false; // 성분이 다른게 하나라도 있으면 거짓을 반환
}
return true; // 참
}
int main() {
for(int i = 'a'; i <= 'z'; i++) tr[i] = i - 'a';
tr['z' + 1] = 'z' + 1 - 'a';
int n, m;
scanf("%d %d",&n,&m);
for(int i = 1; i <= n * 2; i += 2) {
scanf("%s",o[i]);
for(int j = 0; j < m; j++) o[i - 1][j] = 'z' + 1;
}
for(int i = 0; i < m; i++) o[n * 2][i] = 'z' + 1;
n *= 2;
n++;
long long ans = 0;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) for(int k = 0; k < 27; k++) cnt[j][k] = 0;
for(int j = i; j < m; j++) {
for(int k = 0; k < n; k++) {
cnt[k][tr[o[k][j]]]++;
int flag = 0;
for(int l = 0; l < 27; l++) if(cnt[k][l] & 1) flag++;
if((flag == 1 && (j - i) % 2 == 0) || flag == 0) impossible[k] = 0;
else impossible[k] = 1;
p[k] = 0;
}
int r, c;
r = c = -1;
for (int k = 0; k < n; k++) {
if (r >= k) p[k] = min(r - k, p[c * 2 - k]);
else p[k] = 0;
// 성분을 거대한 알파벳으로 보고 manacher's algorithm을 돌린다.
while (k + p[k] + 1 < n && k - p[k] - 1 >= 0 && equal(k + p[k] + 1, k - p[k] - 1)) p[k]++;
if (k + p[k] > r) {
r = k + p[k];
c = k;
}
}
for(int k = 0; k < n; k++) { // 직후 그 값을 더해준다.
if((k & 1) && !impossible[k]) {
ans += (p[k] + 1) / 2;
}
if(!(k & 1)) {
ans += p[k] / 2;
}
}
}
}
printf("%lld\n", ans);
return 0;
}
Prefixuffix
이 링크를 통하여 문제를 확인할 수 있다. 이 문제는 cyclically equivalent 한 prefix와 suffix를 찾는것인데, 일단 cyclically equivalent가 무엇이냐면, “abbaab” 와 “abaabba” 같이 한 문자열을 회전 시킬때 마다, 즉 맨 앞에 있는 문자를 뒤로 보내거나, 맨 뒤에 있는 문자를 맨 앞으로 보내는 행위를 여러번해서 동일하게 만들 수 있는 문자열을 cyclically equivalent 하다고 한다. 이때 주어진 문자열의 prefix와 suffix중에 cyclically equivalent한 것을 찾는 문제이다.
먼저 생각해볼 수 있는 것은 $O(N^{2})$ 풀이로서 그냥 맨 앞부터 for를 돌리면서 맨 뒤에서 $[n-i-1, n-1]$ 범위와 $[0, i]$ 를 비교하는 것이다. 당연하게도 이 방법은 개선할 여지가 단 하나도 없다. 그렇다면 이 문제를 해결하려면 무슨 방법을 써야할까? 그것은 단어를 섞는것이다. 일단 홀수의 경우 가운데 문자열은 항상 안쓰게 되니 제거하여 짝수 문자열의 경우만 생각해보자.
먼저 $\frac{n}{2}$ 으로, 즉, 반절 씩 쪼갠뒤, 짝수 번째엔 $[0, \frac{n}{2} - 1]$ 홀수 번째엔 $[\frac{n}{2}, n - 1]$를 차례로 넣는다고 하자. 이때 조심해야할것이 suffix 이므로 $[\frac{n}{2}, n - 1]$는 뒤집어서 넣어준다고 하자.
이렇게 되면, $s_{0} s_{n-1} s_{1} s_{n-2} s_{2} s_{n-3} s_{3} s_{n-4} …$ 이런식으로 반복되어서 들어가게 되는데 여기서 여기서 $s_{0}$ 부터 시작하는 팰린드롬을 구하게 되면 그것이 prefix 와 suffix가 같은 경우임을 알 수 있다. (직접 증명해보자.) 그러면 남은것은 무엇일까? cyclically equivalent 한것을 찾는것이 우리 최초 목표였는데 그 목표는 의외로 쉽게 풀린다. 다시 재조립된 문자열을 $S$ 라고 하자. $S$ 에서 시작지점을 포함한 팰린드롬과 그 팰린드롬과 맞닿는 지점에서 시작하는 팰린드롬 두개를 구해서 합친것중 제일 긴것을 구하는 문제로 변형할 수 있다! 이는 set을 이용하여 매우 간단하게 구할 수 있으니 manacher와 set을 적당히 조합해서 해결하면 된다. 이때의 시간복잡도는 $O(N log N)$
아래는 위 풀이를 구현한 코드이다.
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#define MAXN 2000100
using namespace std;
int p[MAXN];
char o[MAXN];
char u[MAXN];
set<int> pre;
int main() {
int n;
int r, c;
r = c = -1;
scanf("%d",&n);
scanf("%s",u);
if(n == 1) {
printf("0\n");
return 0;
}
if(n & 1) { // 홀수인 경우 가운데 문자는 쓸모가 없다. 제거한다.
for(int i = n / 2; i < n - 1; i++) u[i] = u[i + 1];
u[n - 1] = '\0';
n--;
}
reverse(u + n / 2, u + n); // 뒤집어준다.
int x = 0, y = n / 2;
for(int i = 0; i < n; i++) { // 섞는다.
if(i & 1) o[i] = u[y++];
else o[i] = u[x++];
}
for (int i = n - 1; i >= 0; i--) {
o[(i << 1)+1] = o[i];
o[i << 1] = '#';
}
n <<= 1;
o[n++] = '#';
for (int i = 0; i < n; i++) {
if (r >= i) p[i] = min(r - i, p[c * 2 - i]);
else p[i] = 0;
while (i + p[i] + 1 < n && i - p[i] - 1 >= 0 && o[i + p[i] + 1] == o[i - p[i] - 1]) p[i]++;
if (i + p[i] > r) {
r = i + p[i];
c = i;
}
}
int ans = 0;
pre.insert(0);
for(int i = 0; i < n; i += 2) { // 팰린드롬 두개를 엮어서 제일 긴 문자열을 만드는지 확인한다.
set<int>::iterator it = pre.lower_bound(i - p[i]);
if(*it >= i - p[i]) {
int tmp = *it - (i - p[i]);
tmp = p[i] - tmp;
if(ans < i + tmp) ans = i + tmp;
}
if(i - p[i] == 0) pre.insert(i + p[i]);
}
printf("%d\n",ans / 4);
return 0;
}
마무리
이 포스트를 통해 문자열 알고리즘, 그중에서도 Palindrome 문제를 manacher 알고리즘을 통하여 해결하는 다수의 문제를 보았다. 매우 지엽적인 알고리즘인 만큼 출제가 잘 되는 편은 아니지만, 활용도가 매우 높고, 문제 만드는 입장에서는 온갖 테크닉으로 상대방을 괴롭힐 수 있는 알고리즘이므로 꼭 알아두면 좋겠다 싶어서 이렇게 리뷰해 보았다. 이를 통해 CP 를 준비하는 모든 사람에게 도움이 되었으면 좋겠다.
참고자료
- geeksforgeeks.org; Manacher’s Algorithm – Linear Time Longest Palindromic Substring. Geeks for Geeks
- opanhejia.blogspot.com; Longest palindrome substring. Hejia Pan