목차
개요
이 포스트를 쓰며
이번 포스트에서 살짝 양심고백을 한다면, 원리를 100% 이해하지 못하고 그 구현과 구현체만을 응용하는 것을 다루는 것을 리뷰하려고 합니다. Suffix Automaton의 구현과 동작이 모두 $O(N)$에 이루어지기 때문에 그 효율성 때문에 사용만 가능하다면 매우 유용할 것 입니다. Suffix Automaton의 원리를 전부 이해하고 구현한다면 참 좋겠지만, 아직 몇가지 소정리에 대해서 더 공부해야 이해가 제대로 될 것 같아서 구현방법만 집중적으로 설명하고, 응용에 초점을 두고자 합니다. 아마도 이번 포스트에서 여러분들이 얻어갈 수 있는 것은 원리 보다는 응용 부분에서 얻어갈 것이 있을 겁니다. 다만, 실전성이 있을지 없을지는 모르겠습니다. 엄청나게 지엽적이고, 거의 대부분의 상황에서 Suffix Array 라는 강력한 자료구조가 있는데 구태여 그것을 놔두고 Suffix Automaton을 구현하는가는 살짝 고민해보아야 할 문제긴 합니다. 하지만, 이러한 지엽적인 알고리즘을 공부함으로서 사고력과 문제해결능력에 조금 더 도움이 되었으면 하여서 이렇게 포스트를 작성해 보았습니다.
필요 사전 지식
계산이론을 들으셨거나 Formal Language 관련 과목, Automata 등의 과목등을 들으신 모든 분들이 구현하는데에 어려움이 없을 것이라 사료됩니다. 기본적으로 Finite Automata에 그 기저를 두고 있고, 상당히 복잡한 원리 이므로 pseudo code를 그대로 C++로 옮기는 과정만 담아서 보여드릴 것 입니다. 원리를 기대하셨다면 정말 송구스럽지만, 참고자료에 첨부한 논문을 봐주세요!
구현
구현 부분에서 먼저 KMP 혹은 Aho-Corasick 등을 구현해본 경험이 있으신 분들이라면 알겠지만, Failure Link가 존재합니다. 즉, 찾는 데 실패한 경우 다음 찾을 위치를 알아내는 Link 입니다. 두번째로는 KMP는 연결 방향이 오로지 실패/성공 두가지 밖에 없지만, Suffix Automaton은 현재 state, 현재 상태에서 다음 어떤 상태로 넘어가는 데 문자를 요구합니다. 이를 테면, ab 라는 상태에서 abc로 넘어가려면 c 값을 이용하여 다음 상태로 넘어갑니다. 이는 아호코라식과 유사하나, 트리가 아닌점 등을 고려하면 차별점이 있습니다. 먼저 아래의 Pseudo code를 봐주세요.

Suffix Automaton 을 구현하기 위한 뼈대입니다. 먼저 Q, i, T, E 에 대해서 각각 역할이 무엇인지 설명드리겠습니다. Q는 상태들의 집합을 말합니다. 저희는 배열로 구현할 것이기 때문에, 숫자들의 집합으로 볼 수도 있겠네요. 그 다음 i는 Initial Position, 즉, 시작지점을 의미합니다. T는 Terminal의 약자로 터미널 상태들의 집합을 의미합니다. 터미널이 무엇이냐면 계산이론에서 finite state machine의 승인 지점, 즉, 끝나는 지점을 의미합니다. 마지막 E는 transition의 집합을 의미합니다. 이는 상태 전이 함수, 구현부분에서 설명한 현재 상태에서 다음 어떤 상태로 넘어가기 위한 함수입니다. 이는 맵으로 구현할 수 있습니다. 그 다음은 F인데 F는 Failure Link를 의미합니다. 그리고 Length는 해당 상태에서 가질 수 있는 가장 긴 부분문자열의 길이를 의미합니다. 이는 응용 부분에서 최장 공통 부분 문자열을 찾을때 매우 유용하게 사용됩니다. 또한 Suffix Automaton을 구성하는데 제일 중요한 역할을 합니다. last는 말 그대로 가장 마지막에 생성된 상태를 의미합니다.
그러면 먼저 구조체 구성을 살펴볼까요?
#include <cstdio>
#include <map>
using namespace std;
int last;
int new_state = 0;
int state_createion() {
return ++new_state;
}
struct node {
int terminal; // Terminal
int F; // Failure Link
int Length; // max length
map<char, int> delta; // transition
}e[2000010];
저는 E를 소문자 e로 나타내었습니다. 배열을 이용하므로 새로운 상태가 추가될때마다, 숫자를 증가시키는 방법으로 구현하기로 하였습니다. 위의 함수가 그러한 구현을 나타내 줍니다.
그 다음은 pseudo code의 본격적인 구현을 살펴볼까요?
void construct_sa(char *x) {
for(int c = 0; c <= new_state; c++) { // clear Q, E
e[c].terminal = e[c].F = e[c].Length = 0;
e[c].delta.clear();
}
new_state = 0;
int i = state_createion();
e[i].Length = 0;
e[i].F = 0; // NIL
last = i;
for(int l = 0; x[l] != '\0'; l++) {
sa_extend(x[l], i); // pass x's l-th char, and initial position
}
int p = last;
while (p != 0) { // p != NIL
e[p].terminal = 1;
p = e[p].F;
}
}
짜잔, 있는 그대로 따라 구현하면 됩니다. 문자열을 파라미터로 입력 받은 뒤, Q와 E를 초기화 하는 작업, 즉 map을 전부 비워주고 모든 값을 0으로 초기화 해주는 작업이 맨 위의 for문에서 확인할 수 있습니다. 그리고 new_state를 0으로 초기화 해주죠.
참고로 제 코드에서 ‘'’NIL 혹은 NULL 역할을 하는 것은 0 입니다.’’’ 상태는 1-base를 활용하므로 1부터 시작합니다. p등의 간단한 레지스터는 그냥 pseudo code에 나온 p그대로 이름 변경없이 사용하였습니다.
이제 중요한 SA-EXTEND, 즉, Suffix Automaton의 확장 함수를 살펴보도록 합시다.

상당히 복잡해보이죠? 하지만 걱정하지마세요. 실제 구현은 매우 간단합니다. 먼저 delta 함수에 대해서 언급을 드리자면 transition 입니다. 즉, 다른 상태로 이동하기 위한 함수이죠. 이는 위에서 map으로 구현되어 있습니다. 이제 코드로 한번 살펴보시죠.
void sa_extend(char xl, int i) { // i = initial position
char a = xl;
int newlast = state_createion();
e[newlast].Length = e[last].Length + 1;
int p = last;
while(p != 0 && e[p].delta.count(a) == 0) {
e[p].delta[a] = newlast; // E <- E + {(p, a, newlast)}
p = e[p].F;
}
if (p == 0) e[newlast].F = i;
else {
int q = e[p].delta[a];
if(e[q].Length == e[p].Length + 1) e[newlast].F = q;
else {
int q_prime = state_createion(); // make new suffix state
for(auto &v : e[q].delta) e[q_prime].delta[v.first] = v.second; // E <- E + {(q', b, delta(q, b))}
e[q_prime].Length = e[p].Length + 1;
e[newlast].F = q_prime;
e[q_prime].F = e[q].F;
e[q].F = q_prime;
while(p != 0 && e[p].delta.count(a) && e[p].delta[a] == q) {
e[p].delta[a] = q_prime; // E <- E - {(p,a,q)} + {(p, a, q')}
p = e[p].F;
}
}
}
last = newlast;
}
자주 노드라고 하겠지만, 상태와 노드를 같은 뜻으로 이해해주세요. 혼용하여 사용하겠습니다.
새로운 노드를 만들고 거기에 transition을 추가하는 과정입니다. pseudo code에 있는 그대로를 따라 썼으며 약간 변형이 된 부분은 이해하기 쉽도록 주석처리를 해놓았습니다. 새로운 상태를 만든 뒤, last로 부터 length를 +1 해줍니다. 그리고 last node의 Failure Link를 타고 가면서 새롭게 생성된 노드에 추가적으로 연결해줍니다.
이제 뒤에 나오는 부분이 Suffix Automaton의 핵심부인데, 그렇게 Failure를 타고가다가 한번도 다음 노드로 넘어갈 수 없었다면 당연하게도 새롭게 생성된 노드의 Failure Link는 초기지점 i를 가르키게 될것입니다. 그 지점과 연결해줍니다. 그러지 않은 상황은 어떻게 처리하느냐. 가장 먼저 Failure의 후보가 될 수 있는 지점과 Failure를 타고가다가 처음으로 다음 노드로 넘어갈 수 있는 지점 두개의 Length 의 차이가 1이 되는 지점이라면(더 정확히는 1이 더 높아야합니다), Failure의 후보지인 q를 새로운 노드의 Failure로 연결해줍니다.
만약 그렇지 않다면? 여기가 바로 각 노드들이 문자들이 1 증가할때마다 늘어나는 것이였다면 Suffix 정보를 저장하기 위해 생성되는 가상노드를 만들어야 할 것 입니다. 아래 작업이 그러한 작업입니다.
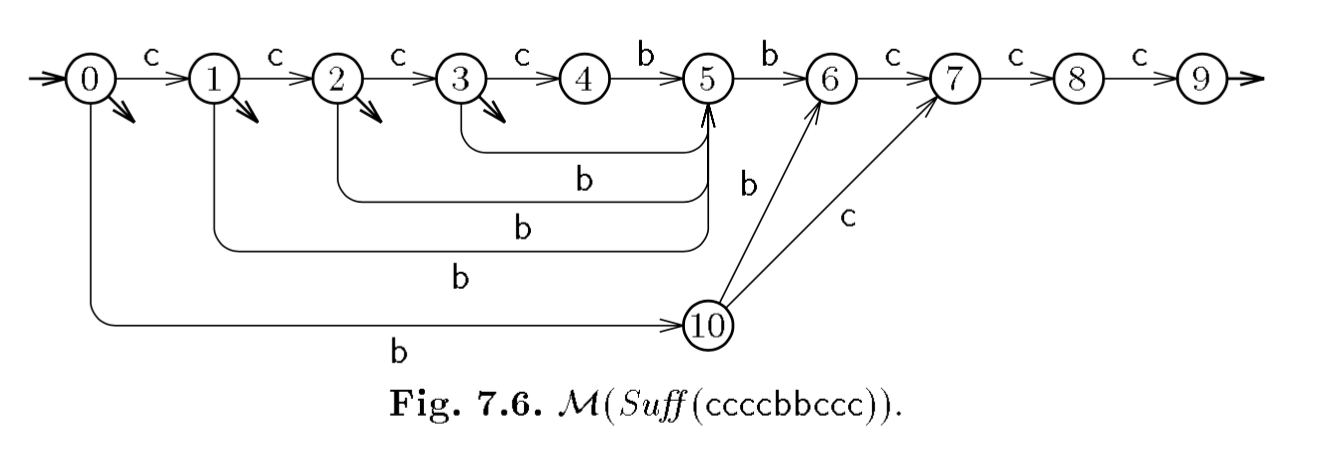
이 그림은 정상적으로 문자열 “ccccbbccc”의 Suffix Automaton이 생성되었을때의 그림입니다. 실제로 그렇게 되는지 pseudo code의 흐름을 따라가거나 저의 코드를 분석해보세요.
응용
패턴 찾기
그렇다면 이번 포스트의 핵심인 응용에 대해서 같이 알아봅시다. Suffix Automaton을 대회에서 낸다면 가장 크게 응용할 요소는 어떤 문자열 s에 대해 여러개의 패턴 p가 그 문자열 s안에 들어있는지 검증하는 곳에 사용할 수 있을 것 입니다. 이것은 매우 간단한 일입니다. 그냥 패턴 p를 순서대로 Suffix Automaton에 넣어보면서 Failure Link를 타지 않고 한번에 이동이 가능하다면 그 패턴은 존재하는 것입니다. 이것의 구현은 후술할 문제풀이에서 구현하는 과정을 보여드릴 것 입니다.
최장 공통 부분 문자열
두번째로 응용할 요소는 바로 최장 공통 부분 문자열을 찾아내는 방법입니다. 일단 문제 하나를 살펴볼까요? 이 문제는 최장 공통 부분 문자열을 찾는 아주 심플한 문제입니다. 우선 이 문제를 풀기 위해서는 최장 공통 부분 문자열을 찾는 알고리즘이 필요하겠지요? 이것에 대한 pseudo code는 다음과 같습니다.

이 pseudo code 는 최장 공통 부분 문자열을 구하는 과정을 적은 pseudo code는 아니지만 L 부분에 l의 최대값을 저장하는 방향으로 실제 구현을 약간 수정하면 최장 공통 부분 문자열을 구하는 코드로 바꿀 수 있습니다.
그렇다면 최장 공통 부분 문자열을 구현해볼까요? 한번 코드로 함께 살펴보시죠.
char o[200010], u[200010];
int main() {
scanf("%s", o);
construct_sa(o);
scanf("%s", u);
int ans = 0, anspos = -1;
int s = 1, len = 0;
for(int i = 0; u[i] != '\0'; i++) {
while(s != 0 && !e[s].delta.count(u[i])) {
s = e[s].F;
if(s != 0) len = e[s].Length;
}
if(s == 0) {
s = 1;
len = 0;
}
else {
s = e[s].delta[u[i]];
len++;
}
if(ans < len) {
ans = len;
anspos = i;
}
}
printf("%d\n", ans);
for(int i = anspos - ans + 1; i <= anspos; i++) printf("%c", u[i]);
printf("\n");
return 0;
}
for 부분부터 쭉 구현한 것이라고 보면 됩니다. ans가 L이라고 생각하고 L = Ll 부분이 완전히 소실되고 max값을 구하는 것으로 대체 되었네요.
그 밖에 또 응용할 요소가 무엇이 있을까요?
서로 다른 부분 문자열의 개수
바로 서로 다른 부분 문자열의 개수를 구할 수 있습니다. Initial Position 에서 시작하여 발생하는 모든 경로들이 모든 부분 문자열을 나타낼 수 있음을 알 수 있습니다. 그렇다면 이것을 전부 재귀함수로 traversal 하면 당연하게도 엄청난 시간이 들겠지요? 이것을 막기 위해서 memoization 을 하면 됩니다. 처음 자기자신을 포함한 +1 한 값을 계속해서 리턴하는 방식이지요. 한번 코드로 살펴볼까요?
long long dp[2000010];
long long dfs(int u) {
if(dp[u] != -1) return dp[u];
long long ans = 0;
for(auto &v : e[u].delta) {
ans += dfs(v.second);
}
return dp[u] = ans + 1;
}
네 이런식으로 매우 간단하게 구현할 수 있습니다. memoizaition 만 사용하면 말이죠! 주의할점은 아까도 말했듯이 자기 자신을 +1 해줘야 한다는 점입니다. 하지만 initial position에 해당하는 1번은 빈 문자열이기 때문에 자기자신은 포함해선 안됩니다! 따라서 순회가 모두 끝나고 난 다음에 dp[1] - 1 한 값이 서로 다른 부분 문자열의 개수라고 볼 수 있습니다.
문제풀이
Threatening Letter
이 문제는 농부 존이 불화가 생긴 이웃집에게 복수하기 위해 무시무시한 편지를 쓴다는 무서운 문제입니다. 범죄 예고처럼 글자들을 잡지에서 떼어내서 편지지에 붙여서 누가 쓴건지 모르게끔 하는 문제이죠. 전문 설명은 여기서 그만 두고 진짜 본문제를 살펴보면 농부존은 근데 매우 게으른 사람이었기 때문에, 한조각 한조각 짜르지 않고, 한 구절을 잘라내는 것을 생각해냈습니다. 여기서 한 구절이란 연속적인 부분문자열로, 다음 줄로 넘어가도 잘라낼 수 있음에 유의하세요. 그리고 여기서, 하나더, 동일한 잡지가 무한개가 있다는 점 입니다. 그럼 이제 원하는 결과물이 무어냐로 넘어가면, 최소한의 잘라내는 횟수로 원하는 문자열을 만드는 것이 목표입니다.
즉 본문의 예제에서 FOXDOG 와 DOG를 잘라내어 붙이면 FOXDOGDOG 라는 문자열을 만들어 낼 수 있습니다. 이러면 단 두번의 가위질로 문자열을 만들 수 있으며 이것이 최선이라는 점입니다. 참고로 FOXDOGD OG 이런식으로 입력이 주어졌어도 FOXDOG DOG 식으로 붙일 수 있음에 유의해주세요. 문제를 읽어보면 자세히 나와있습니다.
즉, 우리는 여기서 알아낼 수 있는 점이 현재까지 이어붙인 단어중에서 제일 긴 단어를 찾아내어 붙이는게 가장 최선이라는 점을 알아낼 수 있습니다! FOXD 를 붙이면 이득이 될수가 없습니다. FOXDOG 까지 이어붙여야 하죠. 이 떄, 매번 최선을 찾아내기 위하여 우리는 Suffix Automaton을 사용할 수 있습니다. 위의 첫번째 응용이 바로 그것입니다. 한번 코드를 살펴봅시다.
int main() {
int n, m;
int cnt = 0;
char tmp[83];
scanf("%d %d", &n, &m);
while(cnt != n) {
scanf("%s",tmp);
cnt += strlen(tmp);
strcat(o, tmp);
}
cnt = 0;
while(cnt != m) {
scanf("%s",tmp);
cnt += strlen(tmp);
strcat(u, tmp);
}
construct_sa(o);
int ans = 0; // 여기서 부터 만들 수 있는 제일 긴 단어 찾는 부분
int cur = 0;
while(cur < m) {
int pos = 1;
while(cur < m) {
if(e[pos].delta.count(u[cur])) {
pos = e[pos].delta[u[cur]];
cur++;
}
else break;
}
ans++;
}
printf("%d\n", ans);
return 0;
}
참 간단하죠? 입력받은 것들을 전부 concat 한다음 Suffix Automaton 을 생성하고, 다시 만들고자 하는 문자열을 concat을 통해 만들어 낸 뒤, 주석 처리한 부분에 따라 찾아낼 수 있는 것 중 제일 긴것을 찾아내면 되는 것 입니다.
이런식으로 하면 시간복잡도는 $O(N)$ 이 됩니다.
SUBLEX - Lexicographical Substring Search
이 문제는 문자열이 주어졌을때 그 문자열의 부분 문자열을 사전순으로 정렬했을때 k번째 부분 문자열이 무엇인지 출력하는 문제입니다. 네, 어떤걸 활용해야 할지 바로 감이 오시나요? 바로 서로다른 부분 문자열의 개수를 구하는 dp 배열을 활용하면 매우 쉽게 풀리는 문제입니다.
이는 매우 간단하게 구현할 수 있는데 dp 역추적 하듯이 구현하면 됩니다. 우선 map을 사용했을 테니 각 transition이 사전순으로 정렬된 상태일 것 입니다. 그러면은 해당 transition으로 이동하였을 때, k보다 크거나 같은지 아니면 작은지 확인하고, 작으면 그 transtion으로의 이동을 포기합니다. 아닐 경우 그 transition으로 이동하면서 -1을 해줍니다 동시에 그 문자를 선택합니다. 여기서 -1을 하는 이유는 자기자신, 즉, suffix의 prefix 부분을 제해야 하기 때문이죠. 그러다가 만약 x가 0이 되면 멈추면 됩니다.
구현은 아래와 같습니다.
char anss[200010];
char o[200010];
int main() {
scanf("%s", o);
construct_sa(o);
for(int i = 1; i <= new_state; i++) dp[i] = -1;
dfs(1);
dp[1]--;
int q;
scanf("%d", &q);
for(int i = 0; i < q; i++) {
long long x;
scanf("%lld", &x);
if(x > dp[1]) {
printf("-1\n");
continue;
}
int cur = 1;
int len = 0;
while(x) {
for(auto &v : e[cur].delta) {
if(x - dp[v.second] > 0) x -= dp[v.second];
else {
x--;
anss[len] = v.first;
len++;
cur = v.second;
break;
}
}
}
anss[len] = '\0';
printf("%s\n", anss);
}
return 0;
}
마무리
이번 포스트를 통하여 이 포스트를 읽으시는 분들이 suffix automaton 에 대한 응용을 유연하게 할 수 있게 되었으면 좋겠습니다. 더 다양한 응용과 원리를 알면 할 수 있는 각종 기법들이 존재하지만 저의 부족으로 더 많이 전달 할 수 없음이 안타깝습니다. 다만 다른 분들이 이 포스트를 보고 흥미를 느끼고 원리 까지 분석한 더욱 멋진 포스트가 나오리라 믿습니다.
참고자료
- Maxime Cro chemore, Christophe Hancart; Automata for Matching Patterns; http://www-igm.univ-mlv.fr; pp. 26-40